基于平稳和连续小波变换融合算法的心电信号P,T波检测

熊 鹏 刘学朋 杜海曼 刘 明 侯增广 王洪瑞* 刘秀玲

①(河北大学电子信息工程学院河北省数字医疗工程重点实验室 保定071002)

②(中国科学院自动化研究所 北京100190)

1 引言

心电图(ElectroCardioGram,ECG)作为心血管疾病诊断的有效手段，其P,T波代表了心室的复极化，精准的P,T波检测可以对心室颤动和心源性猝死等重大心脏疾病进行有效预测[1,2]。但是由于P,T波所在位置低频成分较多[3]，噪声较大，加之P,T波形态多变。因此，P, T波检测成为目前的研究难点。

目前，针对ECG信号P,T波的自动检测，研究工作者提出了多种方法，包括基于滤波器的检测算法、基于神经网络的检测算法和基于小波变换的检测算法等。

Elgendi等人[4]通过0.5～10 Hz的2阶巴特沃斯滤波器(Butterworth filter)剔除与P,T波检测无关的基线漂移和QRS波群，利用差分法对P,T波进行识别。通过P,T波频域特性滤除的基线漂移和QRS波群，得到P,T波的待检测段，待检测波段的光滑程度是影响其峰值检测的关键。但是，光滑的仅包含P,T波的待检测段的获得是十分困难的，由于在ECG信号在采集过程中受到外界各种噪声以及工频干扰[5]，因此ECG信号的特征波的波峰附近会有细小的毛刺，这些毛刺的频段与P,T波频段重叠[6]，因此仅通过频域特性对信号滤波并不能去除这种毛刺，从而无法获得光滑的P,T波待检测段，导致峰值点的判断不准确。

Peimankar等人[7]利用已有的小波法获得P波和T波位置，根据P波和T波位置选取附近的采样点作为神经网络的输入，构建训练模型。但是在训练集构建过程中，该类算法对训练集样本的广泛性有一定的要求，因此全面丰富的训练集对提高该类算法的精度是十分重要的，但实际临床中P波和T波形态变化复杂，仅依靠训练集得到的检测模型的适用性低。

小波变换方法对于信号低频成分具有时间局部化程度高的优点，在对于低频成分的奇异点检测有着较好的效果[8]，因此被研究工作者广泛用于ECG信号中低频成分P,T波检测。Yochum等人[9]利用连续小波变换在不同尺度下检测P,T特征波时，并未对数据进行预处理，虽然还原了数据的真实性，但其基线漂移和QRS波群的存在会影响P,T波在其尺度细节下的检测，导致P, T波检测精度不理想。为了解决基线漂移和QRS波群的干扰问题，Dev Sharma等人[10]在利用小波变换检测的基础上，采用对QRS-P波极值对的对消方式仅保留T波极值对，从而有效完成T波的检测。但是，在分解重构过程中，该算法直接将过零点判定为峰值点，这使得检测的过零点在重构到原始信号的峰值点过程会存在错位，从而影响T波检测精度。

综上，虽然现有P,T特征波检测算法取得一定成效，但仍然存在锯齿状毛刺干扰和过零点错位等优化不足之处。基于此，本文提出平稳和连续小波变换融合算法来实现P,T特征波的精准检测。针对毛刺问题，融入平稳小波对其P,T特征波候选段进行平滑处理，平滑后再对P,T波极值对进行精准检测，降低毛刺对P,T波极值对检测带来的干扰。同时，为防止P,T波极值对发生漏检，在所检测到的P,T波极值对左右添加检测窗口，进行极值对的筛选。最后，针对过零点错位问题，根据尺度时移修正原则，对过零点进行时移修正，保证过零点准确还原到原始信号所对应的P,T波峰值点。弥补毛刺干扰和过零点错位带来的误差，实现心电信号P,T波的精准检测。

2 本文方法

如图1所示，本文基于平稳和连续小波变换融合算法的P, T波检测主要包括ECG信号预处理、ECG信号平滑处理和P,T波峰值点检测。首先，利用连续小波变换对其信号进行降噪和R波检测，消除工频干扰、基线漂移等噪声以及提供P,T波检测区间。然后，利用平稳小波变换对其ECG信号待检段进行平滑处理，降低毛刺对P,T波奇异点检测的影响。在平滑ECG信号基础上，本文算法分别对其P,T波极值对进行筛选和过零点时移修正，解决过零点错位问题，最终实现P,T波波峰的准确定位。

图1 P,T波检测流程图

2.1 预处理

本模型采用连续小波变换法[11]对ECG信号进行工频干扰和基线漂移的消除，含有噪声的信号经过连续小波变换后，噪声主要分布在高频小波系数中，而有用信号主要分布在低频小波系数中。通过小波变换将其噪声信号和有用信号进行有效区分，保留有效信号，然后将处理过的小波系数进行重构，即实现工频干扰和基线漂移的消除。

在心电图中，由于R波能量值高，形态特征明显，易于检测，P,T波能量值低，形态复杂多变，但两者在位置上存在顺序规律，故本模型利用小波变换算法对ECG信号的R峰进行检测[12]，从而根据R波检测位置来预判P,T波峰值点检测区间。

2.2 P, T检测尺度平滑处理

针对P,T特征波能量低、形态多变等特征，在检测P,T波峰值点时，其原始信号中存在锯齿状毛刺，干扰P,T波峰值点的准确定位。针对此问题，本文模型利用平稳小波变换对P,T波待检测段对应的尺度信号进行平滑处理，降低毛刺对检测结果造成的影响。

在ECG信号中，不同尺度包含不同频段信号，从而有利于在对应尺度下准确检测其指定特征波[13]。其中，P波的频谱宽度在0～20 Hz，其波峰能量主要集中在3～12 Hz，R波频谱宽度在10～25 Hz,T波频谱宽度在0～8 Hz，其波峰能量主要集中在0～8 Hz。本实验中信号的采样率为360 Hz，经小波分解后，第5层的低频小波系数频带范围为5.76～22.5 Hz，第5层低频小波系数频带范围为5.625～11.25 Hz。因此，根据表1频率分布可知，P,T波在其第4尺度下表现最为明显。所以本模型选取第4尺度分别进行ECG信号的平滑处理和峰值点检测。

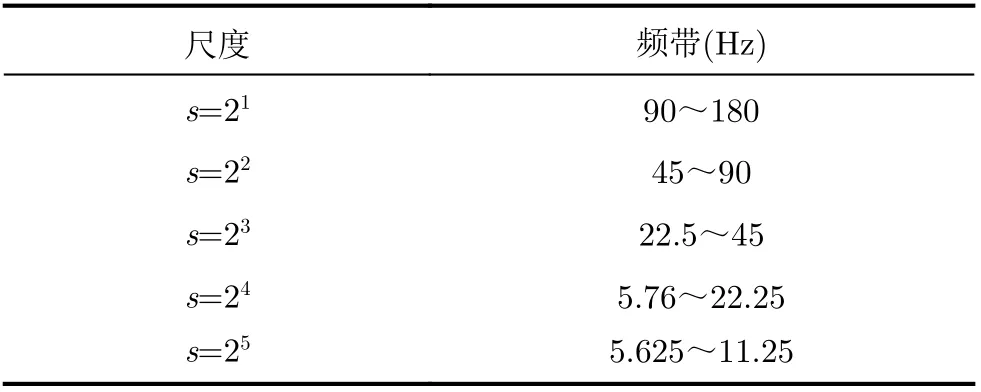
表1 频率分布(Hz)

2.3 P, T波峰值点检测

在平滑的基础上对P波和T波进行奇异点检测，奇异点检测首先要确定奇异点的位置，其位置检测主要利用R波模极值对的位置来判定P波和T波模极值对的位置区间，其中Parea和Tarea为P波和T波位置区间。

P,T波在其s=24尺度下形态最为明显，所以选择在cd4系数上进行P,T波峰值点检测。在R波首个模极值对左侧添加(1/3)·RR，在Parea区间内检测其模极值对，此模极值对由P波生成。同理，在R波最后一个模极值对右侧添加( 1/2)·RR， 在Tarea区间内检测其模极值对，此模极值对由T波生成。

本模型为防止P,T波误检，分别在P,T波模极值对的左右添加100 ms检测窗口，检测是否存在正负性极值对。在存在正负性极值对的情况下，通过去掉模极值对较小的极值，保留其明显的一对极值对，此极值对视为两个极值点，在其极值点前后选取7个采样点，检测是否有同极值点，在对其极值点进行修正，修正后的极值点更新了该极值对，此极值对间的过零点为特征波峰值点。

多尺度下奇异点检测，过零点在重构到原始信号峰值点过程中会存在过零点与峰值点错位问题，本文模型对过零点按照2j−1−1规则进行平移，其中j为分解尺度，不同尺度的过零点修正不同，即本文在检测P,T波时j=4，因此向右平移7个采样点得到最终的过零点，此过零点为修正后的P,T波波峰。

通过对模极值对和极值点左右邻域的筛选与过零点的修正，解决了P,T特征波误检导致检测精度差的问题。

3 实验分析

3.1 数据库

本文所提出的算法在MIT-BIH arrhythmic数据库进行验证[14]，其中102,104,107,217这4组数据采集过程中患者携带起搏器，形态失真，并未纳入本文实验。舍弃这4组数据的同时根据性别随机选取了15名年龄在32～89岁的男性被试心电图和16名年龄在23～89岁的女性被试心电图，构成31条实验数据用于对本文所提算法性能进行测试。每个记录的采样频率为360 Hz，每个记录30 min，本文仿真过程均采用Ⅱ导联心电信号进行验证。

3.2 评估指标

本文利用误差率er、敏感度Se和正确预测度PP3个指标对本文算法检测性能进行评估[15,16]，3个指标具体计算公式分别如式(7)—式(9)所示

其中，FN为没有检出的P,T波峰值点个数，FP为错检P,T波峰值点个数，N为P,T波心拍个数，Rd为正检P,T波峰值点个数。

3.3 平滑处理分析

为验证本文算法对ECG信号平滑处理的有效性和平滑程度对ECG信号P,T波检测影响。例举103.dat心律失常患者数据，图2为该数据平滑处理结果图。其中图2(a)为预处理信号，图2(b)为预处理信号P,T波检测结果，图2(c)为经过平滑处理的预处理信号，图2(d)为经过平滑处理的预处理信号P,T波检测结果(红色和黑色圆圈分别代表P,T波峰值点位置)。图2(a)和图2(c)可以看出，未经平滑处理的信号和经过平滑处理的信号其平滑程度有明显的变化；从图2(b)和图2(d)可以看出，未经平滑处理的信号在检测P,T波时出现峰值点的误检，误将其毛刺点检测为峰值点。而经过平滑处理的信号在检测P,T波时避免了误检的出现。

3.4 时移修正分析

对平滑后的ECG信号进行P,T波峰值点检测，其峰值点的定位是由检测的过零点还原到原始信号中的峰值点，还原过程，不同尺度下P,T波过零点对应的峰值点存在一定的时移误差。针对此问题，本文算法根据尺度分解重构原则对过零点进行时移修正，优化检测算法的不足之处。通过图3可知，图3(a)和图3(b)分别为未经过时移修正和经过时移修正的P,T波检测结果，两者对比发现，当检测P,T波奇异点时对过零点进行时移修正能够准确定位其ECG信号P,T波波峰，从而避免了尺度下检测的过零点经重构环节导致的错位现象，验证了过零点的时移修正对P,T波奇异点检测具有一定的效果，弥补上述小波中对P,T波检测的不足之处。

图2 信号平滑处理结果

3.5 对比结果分析

表2记录了MIT-BIH数据库上P波和T波检测算法的性能。表3提供了该数据库下的P波和T波检测算法性能对比。其中，N为P,T波心拍个数，FN为没有检出的P,T波峰值点个数，FP为错检P,T波峰值点个数，Rd为正检P,T波峰值点个数，分别采用误差率er、敏感度Se和正确预测度PP3个统计参数来评价所提出的P波和T波算法的性能。

图3 信号时移修正结果

表2 P, T波统计结果

表3 方法对比

如表2所示，P波的误差率、敏感度、正确预测度达到：0.23%,99.85%,99.90%;T波的误差率、敏感度、正确预测度达到0.27%,99.85%,99.87%，验证了本文算法的有效性，能够准确有效地检测心律失常疾病下P,T特征波。在心电信号中，由于采集和仪器本身等因素，波峰附近会存在一定的毛刺波形，毛刺的存在，导致峰值点定位不准确。同时，峰值点的定位是由检测的过零点还原到原始信号中的峰值点，还原过程，过零点对应的峰值点存在一定的时移误差，同样导致峰值点定位不准确。本文算法针对锯齿状毛刺干扰、过零点错位等问题进行了优化。在连续小波多尺度P,T波信息获取下，融合平稳小波，对P,T波候选段进行平滑处理，解决毛刺干扰问题，根据不同尺度下的时移修正规则，再进行过零点的时移修正，保证所检测的P,T波过零点能够准确还原到原始信号所对应的P,T波峰值点。本文算法简单有效地优化了现有算法中毛刺干扰、过零点错位等不足，最大限度避免真实峰值点的错误定位，为临床医学分析提供基础保障。

为评估本文算法性能，分别与传统特征波检测算法和基于深神经网络算法进行了比较，如表3所示。文献[4]采用差分法对P,T波候选段进行峰值点检测，虽然通过频域特性消除杂波，得到P,T波的候选段，由于在心电信号采集过程中受到外界各种噪声以及工频干扰，信号本身存在锯齿状细小毛刺，从而干扰峰值点的检测。所以，光滑的仅包含P,T波的待检测段获取是十分困难的。文献[7]运用深度神经网络构建P,T特征波训练模型，虽然此方法不需要消除杂波，但构建训练集过程中，该类算法对训练集样本的广泛性有一定的要求，因此全面丰富的训练集对提高该类算法的精度是十分重要的，仅依靠训练集得到的检测模型在临床应用中适用性低。文献[9]利用小波法检测心电信号P,T特征波，既不存在杂波干扰，也不存在特征波形态的广泛性约束，但信号本身的毛刺问题仍会干扰峰值点的定位，导致现有检测精度并不理想。文献[10]在小波法检测基础上，运用频域和位置信息消除QRS波群和P波极值对，仅保留T波极值对T波过零点进行检测。但是小波分解重构过程中，由于尺度原因，过零点对应原始信号峰值点存在错位现象，同样带来峰值点的定位误差。虽然现有检测精度相差不大，但特征波的准确定位对是医学特征提取的基础保障。所以，针对上述毛刺干扰、过零点错位等问题，本文利用连续小波多尺度优势获取P,T特征波主要成分，融合平稳小波对P,T波候选段进行平滑处理，再根据尺度分解重构原则对过零点进行时移修正，优化检测算法的不足之处，为远程医疗心电信号智能分析提供准确的定位。

4 结束语

本算法使用MIT-BIH arrhythmic数据库中6种常见且具有临床研究意义的心律失常心电信号对该算法进行了测试和评价。针对现有检测算法存在的锯齿状毛刺干扰和过零点错位问题，运用融合算法优化不足之处，最大限度降低毛刺、过零点错位带来的误差。实验结果表明本文算法的P波误差率、敏感度、正确预测度可以达到0.23%,99.85%,99.90%；T波误差率、敏感度、正确预测度可以达到0.27%,99.85%,99.87%，能够对这6种心律失常疾病下的心电信号P波和T波进行峰值点的准确定位。与现有P,T波检测算法相比，本文算法简单，执行效率高，面向临床应用具有明显优势。另外，本文的实验数据仅包含了6种常见心律失常，没有考虑更多的心血管疾病情况，下一步将对该算法进行优化，进一步提高在多种疾病数据下的P,T波检测精度，为心血管疾病智能辅助诊断提供基础保障。