双材料界面裂纹复应力强度因子的正则化边界元法1)
谷 岩 张耀明
∗(青岛大学数学与统计学院,山东青岛 266071)
†(山东理工大学数学与统计学院,山东淄博 255049)
引言
双材料比较容易在结合面附近萌生裂缝,并沿着界面发生扩展直至结构破坏.因此,双材料的破坏不仅表现为单一材料内部的裂纹问题,往往更多的是界面的破坏、开裂或脱黏[1].随着计算力学学科的不断发展,用于解决断裂力学问题的数值计算方法不断涌现,从早期的有限差分法[2]、有限元法[3]、边界元法[4-9]到现在的无网格法[10-11]、数值流形法[12]、非连续变形分析法[13]、分子动力学法[14]等,它们成为推动断裂力学研究不断发展的重要工具.
采用数值方法进行断裂力学分析时,裂纹尖端奇异区域处理的好坏直接关系到最终断裂力学参数(如应力强度因子、能量释放率等)的求解精度.对于传统单一材料,材料内部裂纹尖端位移和应力场具有经典的平方根(r1/2)和负平方根(r−1/2)渐近性,相应的理论研究和数值求解技术已发展的非常成熟.比如对裂尖奇异应力场的求解,已发展了包括“1/4 单元法”、“数值外插法”、“虚拟裂纹闭合法”和“J 积分/相互作用积分”等多种有效的求解方法.然而,与传统单一材料不同,双材料界面裂纹渐近位移和应力场表现出剧烈的振荡特性,即[15-16]
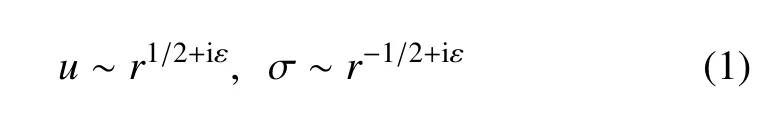
其中i 为复数单位,ε 为双材料参数(或振荡因子).导致许多用于表征经典的平方根和负平方根物理场渐近性的传统方法失效[17-18].虽然界面裂纹复应力强度因子(K1+iK2)可采用各种守恒积分(如J 积分)或位移外插法等进行间接求解,但计算精度较低,也难以直接获得裂尖近场区域物理量的精确分布[19].因此,虽然目前计算断裂力学发展的比较成熟,但其在双材料界面裂纹分析方面的研究依然比较欠缺,从基础研究的角度来考虑还需进行大量的研究.
此外,随着实际工程需求和表面涂层工艺的逐渐成熟,大量双材料的相对厚度(表面特征长度和厚度的尺寸比)越来越小,特别是各种微纳米复合材料的相继出现,给精确有效的数值模拟带来了巨大的挑战.比如,为了避免出现畸形网格,有限元法需按照涂层的厚度划分单元.可这样做必然会导致百万甚至几百万个子单元,计算工作量剧增,同时解的收敛性也难以保证[20].相对于有限元法,边界元仅需在边界离散,可以从容处理边界单元的疏密过渡,很大程度上避免了有限元法中网格畸变带来的困难,这一点对薄体与涂层结构问题的数值模拟尤为重要.近年来,边界元法在薄体结构问题中的应用正在蓬勃发展,被认为是其比有限元法更具优势的一个新领域,而且在表面涂层、压电薄膜等工程领域展现出了广阔的应用前景[21-27].
论文以边界元法为基本工具,通过引入一种能精确表征复合材料界面裂纹振荡特性的“特殊裂尖单元”[28],实现了双材料界面裂纹复应力强度因子的精确求解.该方法无需裂尖区域高密度的网格剖分,可显著提高裂尖近场力学参量和复应力强度因子的求解精度和数值稳定性.在此基础上,结合边界元法中计算近奇异积分的一种通用正则化算法[29-30],成功求解了超薄双材料界面裂纹问题.数值算例表明,所提算法稳定,效率高,在不增加计算量的前提下,显著提高了裂尖近场力学参量和断裂力学参数的求解精度和数值稳定性.
1 界面裂纹渐进位移和应力场的振荡特性
图1 中,考虑由两种不同材料组成的双材料板,在板的结合面存在一条界面裂纹.记上层和下层材料分别为区域Ω1和Ω2,相应的弹性模量和泊松比分别为µ1,ν1和µ2,ν2.
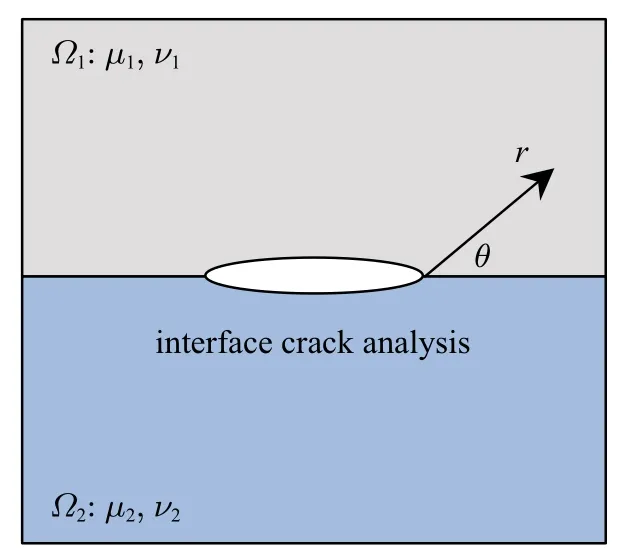
图1 双材料界面裂纹问题Fig.1 An interface crack in a dissimilar material
早在20 世纪五六十年代,Williams[16],Erdogan[15]和England[17]等就发现双材料界面裂纹渐近位移和应力场具有形如式(1)的振荡特性.其中r为计算点到裂尖的距离,双材料参数ε 定义如下

对于平面应变问题,有κi=3 −4νi.对于平面应力问题,有κi=(3 −νi)/(1+νi).裂纹尖端附近的位移和应力场可表示为[28,31]
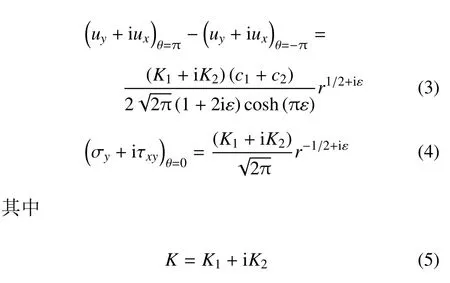
K为复应力强度因子,ci=(1+κi)/µi为材料常数.由式(3)或式(4)可知,复应力强度因子K1+iK2的值可通过裂尖张开位移或应力进行数值求解.
传统有限元方法在处理裂纹问题时,需严格按照材料界面剖分网格,且裂尖区域需要采用高密度网格以捕捉应力场的奇异性,前处理工作比较繁琐.此外,需要指出,界面裂纹渐近位移和应力场具有r1/2+iε和r−1/2+iε的振荡特性,许多用于表征经典的平方根和负平方根物理场渐近性的传统方法失效,这也给双材料界面裂纹精确有效的数值模拟带来了不小的挑战.
2 求解界面裂纹问题的边界元方法
采用多域边界元法对图1 所示的双材料界面裂纹问题进行数值求解.对区域Ω1和Ω2,可分别建立如下边界积分方程[28]

其中P和Q代表计算点和边界积分点,uj和tj(j=1,2)代表边界位移和面力,Uij(P,Q)和Tij(P,Q)为位移和面力基本解.对于光滑边界,Ci j(P)=δi j/2.为了保证足够的计算精度,采用三点二次非连续单元近似(图2).边界元法中的单元近似分为对边界形状的“几何近似”和对边界物理参量的“物理近似”.对几何边界的近似可表示为
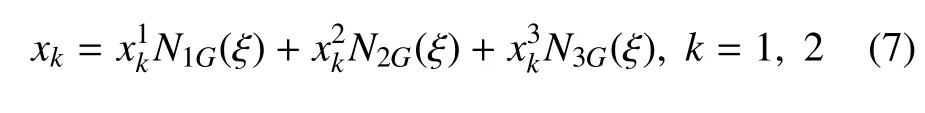


图2 二次非连续单元Fig.2 Discontinuous quadratic element
将边界积分方程(6)分别应用于区域Ω1和Ω2,可构造如下线性代数方程组

其中H和G代表系数矩阵,上标“1”和“2”分别表示区域Ω1和Ω2,下标“I”代表双材料结合面(界面)处对应的系数矩阵或物理量.根据界面位移和面力的连续条件

方程组(12)和(13)可以耦合为
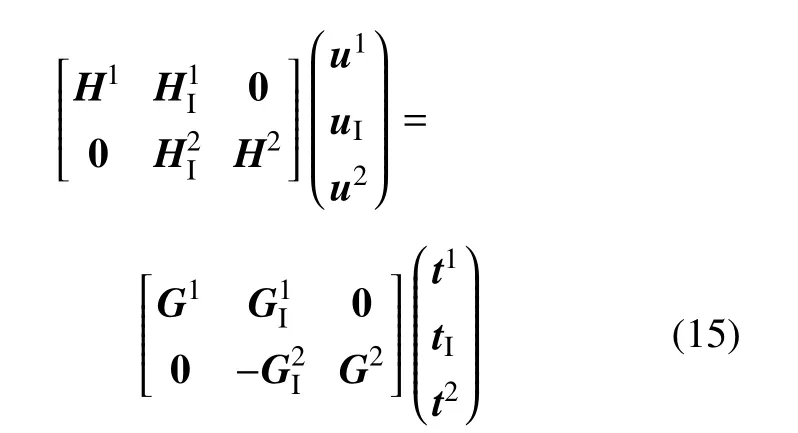
通过对方程(15) 的求解,可得到边界点处位移和面力的数值解.将裂纹尖端的张开位移或面力代入式(3) 或式(4),便可进一步求得复应力强度因子的值.
需要指出,界面裂纹渐近位移和应力场具有r1/2+iε和r−1/2+iε的振荡特性.因此,在采用以上分域法的同时,需要对裂尖单元(包含裂纹尖端的左右两个单元,见图3)进行特殊处理,这就是接下来要引入的“特殊裂尖单元”法.
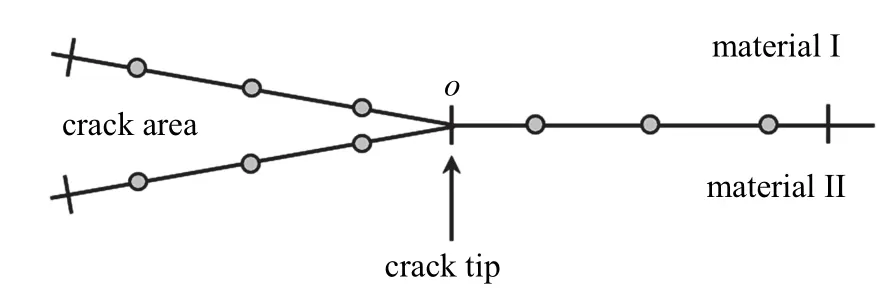
图3 界面裂纹裂尖单元Fig.3 Elements near the crack-tip
3 双材料界面裂纹“特殊裂尖单元”
引入一种含有复振荡因子的新型“特殊裂尖单元”[28],可精确表征裂纹尖端渐近位移和应力场的振荡特性.提高界面裂纹复应力强度因子的数值求解精度.下文简要介绍方法的数学原理.
对于几何边界的近似,裂尖单元采用如式(7)和式(8) 相同的二次单元.但对于位移和面力的近似(物理量的近似),裂尖单元需要做如下特殊处理.如式(3) 所示,为了准确表征裂尖位移场的振荡特性,裂尖位移场在数学上应该具有以下形式
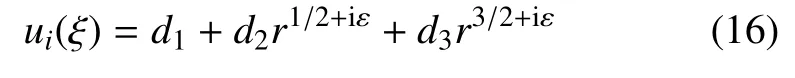
其中d1代表刚体位移,d2r1/2+iε为主要项,d3r3/2+iε为距离函数r的高阶无穷小量(对计算精度的影响可以忽略).
数值上,通过式(9) 插值得到的裂尖位移场应具有如式(16)的渐进性.当裂纹尖端在单元中的无因次坐标为ξ=−1 时,即裂尖位于单元左端点时(图3),式(9) 中的位移插值形函数应表示为以下形式


4 薄体结构边界元法中近奇异积分的计算
薄体结构问题的数值求解是边界元法的难点之一,其实质是近奇异积分的精确计算.原因是,受薄体结构特殊几何构造的影响,边界节点通常和某些积分单元十分地接近,导致边界积分方程(6)的积分表现出不同程度的近奇异性,常规高斯积分结果失效.本文采用一种非线性变量替换法对近奇异积分进行精确求解.该方法基于尽可能拉近运算因子间数量级或变化尺度的思想,可有效改善近奇异核函数的振荡特性,使近奇异积分的计算结果得到大幅提高.
二维弹性力学边界元法中的近奇异积分可以归结为以下两种形式[32-33]
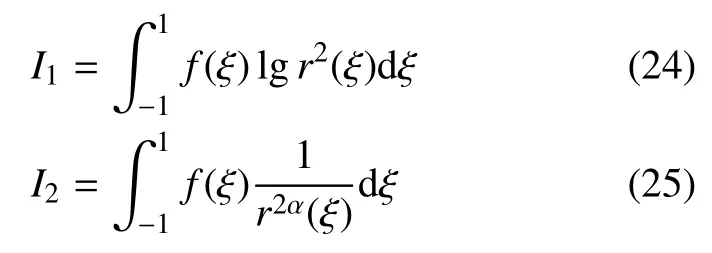
其中α>0,f(ξ)为规则函数(包含雅可比函数、形函数等).若采用三点二次单元近似几何边界,计算点P到积分单元的距离函数r2(ξ)可表示为[32]

其中g(ξ)0 为规则函数,a代表计算点P在积分单元投影的无因次坐标,b代表计算点P到积分单元的最短距离.将式(26)代入式(24)和式(25)可得

上述积分在a点被分为两部分来计算,可提高数值计算精度.在积分区间[−1,a]和[a,1]上分别引入变量替换x=a−ξ 和x=ξ −a,则上述近奇异积分可表示为以下形式
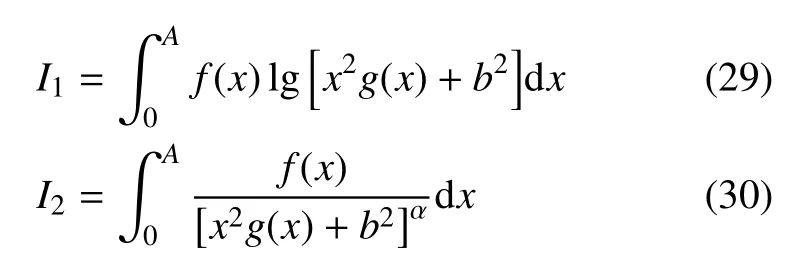
其中A=1+a或A=1 −a.显然,当计算点P到积分单元的最短距离b很小时,上述积分核函数在0 点附近会产生剧烈的振荡特性.为此,引入如下非线性变量替换
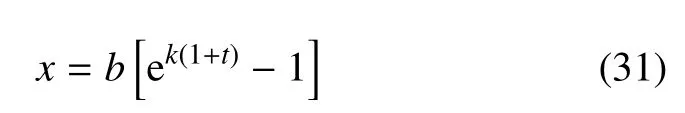
其中k=0.5 ln(1+A/b).将变量替换(31)代入式(30)可得

式(29) 的变换类似可得.因g(·)0 为规则函数,式(32)核函数分母部分(ek(1+t)−1)2g(t)+11 恒成立,原近奇异性得以消除,可通过传统高斯积分进行精确求解.论文首次尝试将上述计算近奇异积分的正则化算法与“特殊裂尖单元”法相结合,数值模拟大尺寸比(超薄) 双材料的界面裂纹问题,下面给出数值算例.
5 数值算例
首先,为验证所提“特殊裂尖单元法”求解双材料界面裂纹问题的有效性,算例1 给出了无限大双材料板受均匀拉力时断裂力学参量和近场物理量的计算结果(不涉及近奇异积分的计算问题).算例2 ∼5侧重于大尺寸比(超薄) 双材料的界面裂纹问题.其中,算例2 和算例3 假设两种材料具有相同的弹性模量和泊松比(应力强度因子存在精确解).算例4和算例5 讨论了不同材料的界面裂纹问题.
例1含有中心裂纹的无限大双材料板,界面裂纹的长度为2a,裂纹表面受均匀拉力σ0(见图4).材料1 和材料2 的泊松比为ν1=ν2=0.2.实际计算中,令双材料板的宽度和高度为50a.边界共划分280 个二次单元,其中裂纹表面划分20 个二次单元,裂尖单元相对于裂纹长度为a/10.断裂力学参数和裂尖渐近位移和应力场的精确解见文献[28].

图4 无限大双材料板界面裂纹问题Fig.4 An infinite bimaterial plate with an interface crack
当双材料弹性模量的比值µ1/µ2不断变化时,表1 和表2 给出了复应力强度因子K1和K2的计算结果.结果表明,即使µ1/µ2=1 000,复应力强度因子的计算结果与精确解依然十分的吻合.需要注意,不论µ1/µ2如何变化,裂纹表面仅划分20 个二次单元,且无需对裂尖单元进行局部加密.
表1 应力强度因子K1/(σ0)的计算结果(例1)Table 1 Normalized SIFs K1/(σ0)(Example 1)
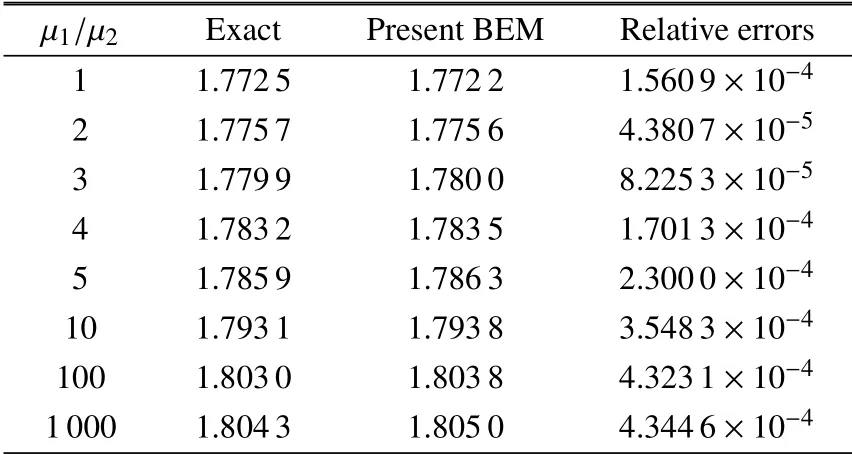
表1 应力强度因子K1/(σ0)的计算结果(例1)Table 1 Normalized SIFs K1/(σ0)(Example 1)
表2 应力强度因子K2/(σ0)的计算结果(例1)Table 2 Normalized SIFs K2/(σ0√)(Example 1)
图5 和图6 分别给出了µ1/µ2=5 时,裂纹表面张开位移和裂尖应力场的计算结果.结果表明所提“特殊裂尖单元法”可精确表征界面裂纹渐进位移和应力场的振荡特性,在不增加计算量的前提下,显著提高断裂力学参数和近场物理量的数值求解精度.图7 给出了裂纹表面剖分单元数量对计算结果的影响(µ1/µ2=5).当裂纹表面划分超过20 个单元时,复应力强度因子的计算结果趋于稳定.
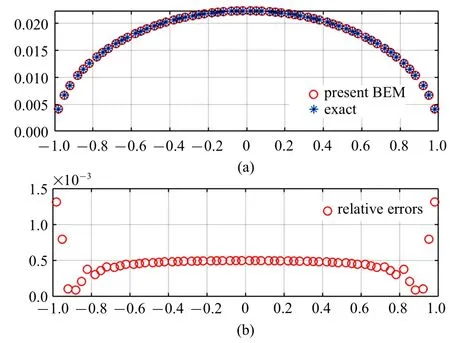
图5 裂纹表面张开位移(a)与相对误差(b)Fig.5 Results of the crack-opening-displacements(upper)and relative errors(lower)

图6 裂纹尖端应力场σy 的计算结果Fig.6 Results of the near-tip stresses σy
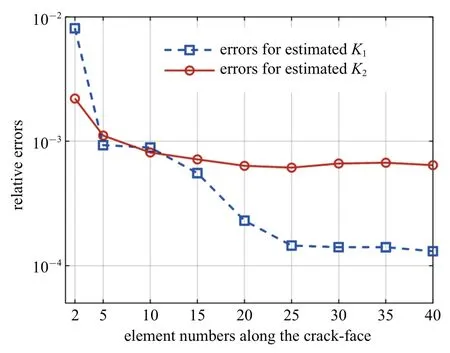
图7 裂纹表面单元数量对计算结果的影响Fig.7 Variation of the errors with respect to the number of crack elements
例2含有中心裂纹的无限大薄板,裂纹的长度为2a,薄板的宽度为2L,厚度为2h,如图8 所示.裂纹上下表面受均匀拉力σ.定义薄板的相对厚度为h/L.当a/h→∞时,应力强度因子的精确解为
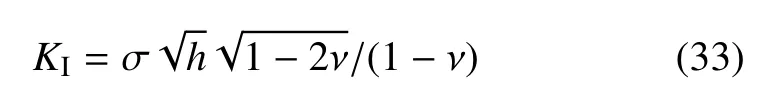
其中ν 为材料的泊松比.边界共划分126 个二次单元,其中裂纹表面划分15 个二次单元.实际计算中,令L/a=20 来近似无限大板.需要注意,边界元法仅需在边界离散,可以从容处理边界单元的疏密过渡.在模拟薄体结构问题时,不需要根据薄体结构厚度的变化对网格进行加密,这是比有限元模拟薄体结构问题有优势的地方.当薄板的相对厚度h/L在10−2∼10−9变化时,表3 给出了无量纲应力强度因子的计算结果.其中,传统边界元法(conventional BEM)指对薄体结构中产生的近奇异积分直接采用传统高斯积分求解.

图8 含有中心裂纹的薄板Fig.8 A central craked thin beam constrained between two rigid grips
表3 的数据表明,当薄板的相对厚度h/L<10−4时,传统边界元法计算的应力强度因子已经完全失效.相比之下,本文算法在薄板的相对厚度小到10−9时,应力强度因子的计算结果依然与精确解十分吻合.

表3 应力强度因子(无量纲K1)的计算结果(例2)Table 3 Results of normalized stress intensity factors K1 (Example 2)
例3边界受剪应力的含有中心裂纹的薄板,裂纹的长度为2a,薄板的高度为2H,宽度为2b,如图9 所示.裂纹长度与板的宽度具有关系b=4a,薄板的高度设置为H=15.定义薄板的相对厚度为b/H.边界共划分188 个二次单元,其中裂纹表面划分10 个二次单元.应力强度因子的精确解为

图9 含有中心裂纹的薄板受均匀剪应力Fig.9 A central craked thin beam under shear loading
当薄板的相对厚度b/H在10−1∼10−9变化时,表4 给出了无量纲应力强度因子的计算结果.表4 的数据表明,当薄板的相对厚度小于10−4时,传统边界元法计算的应力强度因子已经完全失效.相比之下,本文算法在薄板的相对厚度小到10−9时,应力强度因子的计算结果依然与精确解十分吻合.
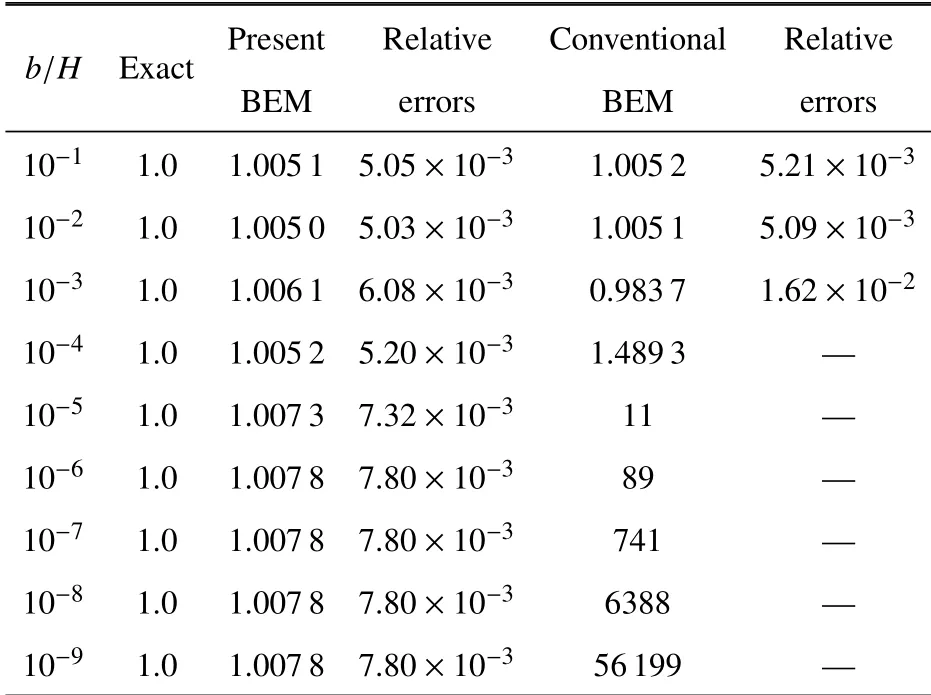
表4 应力强度因子(无量纲K2)的计算结果(例3)Table 4 Results of normalized stress intensity factors K2 (Example 3)
例4含有边裂纹的双材料板,如图10 所示.裂纹的长度为a,材料的厚度为h,宽度为L.板的下边界固定(位移分量为0),左右边界受拉应力,上边界和裂纹表面不受力.材料1 和材料2 的泊松比为ν1=ν2=0.3,弹性模量µ1/µ21.边界共划分320 个二次单元,其中裂纹表面划分5 个二次单元.定义薄板的相对厚度为h/L,裂纹的相对长度为a/h.固定薄板的厚度为h/L=10−4,裂纹的相对长度在0.01a/h0.99 之间变化.表5 给出了不同材料组合时(弹性模量µ1/µ21),复应力强度因子和的计算结果.
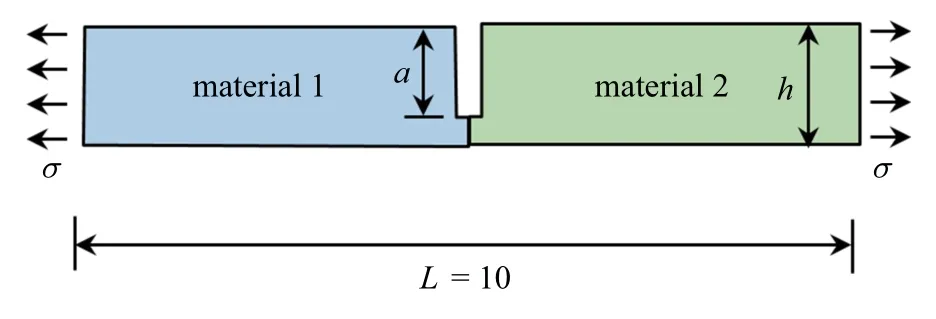
图10 含有边裂纹的双材料板(拉应力)Fig.10 A bimaterial beam with an edge-crack under uniform tensile stress loading
表5 复应力强度因子的计算结果(例4)Table 5 Results of normalized complex stress intensity factors K1/σand K2/σ(Example 4)

表5 复应力强度因子的计算结果(例4)Table 5 Results of normalized complex stress intensity factors K1/σand K2/σ(Example 4)
例5如图11 所示,例5 与例4 具有相同的几何形状,只是边界条件不同.此时,板的下边界固定(位移分量为零),左右边界和上边界不受力,裂纹表面受剪应力.同样,材料1 和材料2 的泊松比为ν1=ν2=0.3,弹性模量µ1/µ21.边界共划分320 个二次单元,其中裂纹表面划分5 个二次单元.与例4类似,固定薄板的厚度为h/L=10−4,裂纹的相对长度在0.01a/h0.99 之间变化.图12 和图13 给出了不同材料组合时,复应力强度因子和的计算结果.随着材料参数µ1/µ2的增大,复应力强度因子的实数部分K1不断增大,而复应力强度因子的复数部分K2不断减小.

图11 含有边裂纹的双材料板(剪应力)Fig.11 A bimaterial beam with an edge-crack under uniform shear stress loading
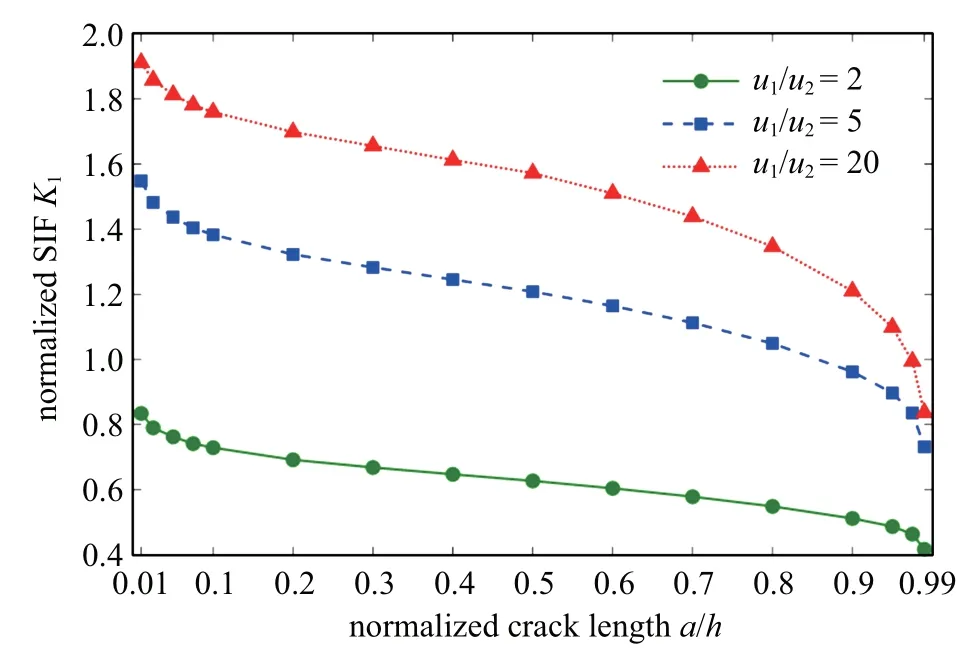
图12 复应力强度因子K1/(τ)的计算结果Fig.12 Results of normalized complex stress intensity factors K1/(τ)

图13 复应力强度因子K2/(τ)的计算结果Fig.13 Results of normalized complex stress intensity factors K2/(τ)
6 结论
针对求解双材料界面裂纹复应力强度因子的困难,引入了一种含有复振荡因子的新型“特殊裂尖单元”.该方法可直接通过裂尖单元的张开位移或界面应力实现复应力强度因子的精确求解,无需裂尖区域高密度的网格剖分,也无需借助J 积分、相互作用积分或虚拟裂纹闭合技术等方法对复应力强度因子进行间接求解.该方法也可直接与有限元或其它数值方法相结合,用于模拟复合材料界面裂纹等相关问题.
此外,将求解薄体结构问题的正则化边界元法与上述“特殊裂尖单元”法相结合,成功求解了超薄(大尺寸比) 双材料的界面裂纹问题.数值算例表明,所提算法稳定,效率高,在不增加计算量的前提下,显著提高了裂尖近场力学参量和断裂力学参数的求解精度和数值稳定性.

