FIR数字滤波器的智能优化算法设计综述

张书玉，王 婷

(南京林业大学 信息科学技术学院，江苏 南京 210037)

0 引言

数字滤波器从单位脉冲响应长度上可以分成两类：有限长冲激响应数字滤波器和无限长冲激响应(Iinite Impulse Response)数字滤波器[1-2]。因为FIR数字滤波器没有反馈，输出仅取决于之前和当前的输入值，始终具有线性相位响应，所以FIR数字滤波器更稳定和易于实现，因此本文只针对FIR数字滤波器做详细讨论。FIR数字滤波器常用的传统设计方法有窗函数法、频率抽样设计法和切比雪夫等波纹逼近法等[3-4]。其中，窗函数法和频率采样法都存在通带和阻带边界频率不易控制、通带波动大和收敛精度低等缺点，因此在实际应用中存在局限性。

数字滤波器的设计和实现中如何克服上述缺陷是个技术难题[5]。鉴于数字滤波器可以通过修改一些预定义的幅度或频率响应来重塑或操纵信号的频谱，因此通过研究和分析将数字滤波器的设计问题转换为多参数优化的问题。由于智能算法在解决许多复杂的、高维的和非线性问题上表现出出色的优化性能，其作为传统数学方法的替代方法可以应用于需要获得全局或近似全局最优解的场合。在数字滤波器的设计上很多智能算法已被应用[6]，例如遗传算法[7]、粒子群算法[8]、差分进化[9]、人工蜂群算法[10]、免疫算法等[11]以及上述算法的混合。这些算法通过定义各种误差函数来寻求满足设计要求的一组滤波器系数，使设计的滤波器的幅频响应与理想滤波器的幅频响应在通带和阻带的误差最小。然而，智能算法在设计数字滤波器时同样面临许多挑战，例如算法可能收敛到局部最优解等。随着研究的逐渐深入，每个算法的性能在慢慢改善，并且用来设计数字滤波器的新算法在不断涌现。

1 FIR数字滤波器的设计技术

1.1 FIR数字滤波器的幅频特性

FIR数字滤波器的系统函数为：

其中h(n)是单位脉冲响应，N是滤波器阶数。

h(n)需要在设计过程中确定其值，它有奇、偶对称两种情况，加上N取值为奇偶两种可能，则线性相位FIR滤波器幅度函数H(ω)有四种情况。为了便于分析，以第一种情况为例。

第一种情况：h(n)=h(N-1-n)，即h(n)关于(N-1)/2偶对称且N为奇数。此时幅度函数可写成：

其中：

理想的幅度函数向量记为Hd(ω)，定义误差向量为：

可以看出，线性相位FIR数字滤波器的设计问题即如何求解系数a(n)使得各种误差函数达到最小，从而实现低通、高通、带通和带阻等不同类型的滤波器。

常见的误差函数有如下几种：

(1)加权逼近误差函数：

(2)平方误差函数：

(3)最小化误差函数：

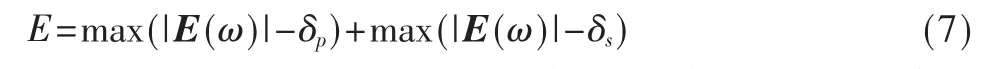
其中G(ω)是用于不同频带中的加权函数，δp、δs分别为通带和阻带波纹。

1.2 传统方法设计数字滤波器

传统窗函数设计方法从时域角度出发，把无限长的脉冲响应hd(n)用有限长的窗函数序列w(n)截取成有限长的脉冲响应h(n)：

窗的点数N及窗的形状是窗函数法中两个极重要的参数。该方法的主要缺点是在频域导致吉布斯效应，因而在具体设计中，通带、阻带波纹的改善通常以加宽过渡带为代价。

频率抽样设计法从频域的角度出发，只是简单地对给定的理想频率响应等间隔采样，然后通过离散傅里叶反变换获得相应的脉冲响应。频率采样法仅在采样点处获得所需的频率响应，在其他点仍然存在误差；可以控制阻带衰减，但通带波纹不易控制。

还有一些较经典的设计方法，例如雷米兹算法可以自由选择滤波器的阶数、通带、阻带以及误差加权函数，但是其计算较复杂。此外加权最小二乘也是比较流行的算法之一，但求解过程中需计算矩阵的逆，在求解高阶矩阵时，逆矩阵求解困难。大多数FIR滤波器的设计方法都只能获得理想滤波器的近似解，随着滤波器阶数的增加，传统方法设计数字滤波器就会更加困难。

1.3 遗传算法优化设计数字滤波器

作为启发式算法的经典算法之一，遗传算法(Genetic Algorithms，GA)的核心在于通过变化和选择来逐步提高一组候选解决方案的质量。在数字滤波器设计领域，遗传算法得到了广泛的关注和研究。自SUCKLEY D[12]首次提出用遗传算法设计数字滤波器以来，已经有超过一百多种使用GA来设计的方案。

SRIRANGANATHAN S[13]1995年提出使用遗传算法来降低数字滤波器复杂度，采用加权逼近误差，使通带和阻带的加权波纹值极小，将此方法和模拟退火方法相比，结果表明遗传算法计算量小。文献[14]用遗传算法设计时分别采用平方误差和加权逼近误差函数，结果表明加权逼近误差函数比平方误差得到的滤波器系数更优。TZENG S T[15]使用一种具有加权功能新的遗传算法，该方法基于迭代复数遗传算法并且用先前的迭代结果来更新每次迭代时的加权函数，通过设计单通带滤波器和复杂的全通滤波器验证算法的有效性。CEN L[16]通过整合自适应遗传算法，模拟退火算法和禁忌搜索算法的主要特征，提出一种混合遗传算法，结果可以大大降低滤波器的归一化峰值波纹的值。文献[17]提出一种将遗传算法与局部优化方法相结合的新型混合遗传算法，根据粒子的多样性来减少搜索空间，并有助于GA摆脱局部最优，从而防止过早收敛，但是需要更多的计算。孙田雨[18]提出通过改进遗传算法的变异交叉的概率和算子两个方面来改善早熟收敛的问题，并且通过实例验证了改进算法的可行性。遗传算法不仅能设计一维数字滤波器，在二维数字滤波器设计上也得到了研究，文献[19]引入稳定性约束条件作为二维数字滤波器的设计标准，通过使用遗传算法来设计二维的数字滤波器，结果能保证滤波器的稳定性。

通常，遗传算法执行时需要交叉和变异算子，由于设置的参数多，用于评估单个功能的执行时间可以长达数分钟或数小时，而使用传统方法时，执行时间不到几秒。计算时间成为制约GA应用的关键瓶颈。实际上，遗传算法应用于特定问题中主要有两个主要缺陷：(1)收敛速度慢；(2)当算法有时找到局部最优解时过早收敛。混合算法可以克服这些问题，但又在计算上增加了难度，迭代过程更加复杂。

1.4 差分进化算法优化设计数字滤波器

为了克服遗传算法在数值优化问题中的缺点，文献[20]引入了进化算法，进化算法的步骤与遗传算法基本一致，主要包括交叉，变异和选择，其优点主要有：(1)仅使用很少的几个控制参数；(2)收敛速度快；(3)无论初始值如何都能找到搜索空间的最小值。文献[21]中分别就进化算法和遗传算法同时利用均方误差函数设计FIR滤波器进行性能比较，结果显示在同样迭代次数下，进化算法大约五六秒就能设计出最佳滤波器，而遗传算法大约70 s，另外进化算法求解的误差函数的结果性能更好。进化算法在文献[22]中与粒子群算法混合用于滤波器的设计，混合优化技术有助于避免粒子陷入局部最小值，并且研究和试验了两种不同的误差函数，结果显示可以实现较小的波纹但需要较大的过渡宽度。文献[23]采用混合萤火虫差分进化算法，结合差分进化和萤火虫技术的优势，通过萤火虫运动增强了差分进化的全局搜索能力。文献[24]中将进化算法与小波突变一起用于设计FIR低通、高通、带通和带阻滤波器，结果显示尽管在通带和阻带的波动较小，但是过渡带宽仍然需要改进。在大多数的启发式算法中，搜索过程本质上是随机并且具有不确定性，这些算法及其改进版本利用它们先前迭代的信息来确定全局最优解，进化算法在其中表现出更快收敛到全局最优解的能力，使其得到广泛的应用[25-31]。

1.5 粒子群算法优化设计数字滤波器

粒子群算法是一种基于社会心理学原理的种群随机优化算法，能够处理多目标函数优化问题。与遗传和进化算法不同，粒子群算法设计数字滤波器设置的参数更少、收敛速度快、计算量小、搜索能力强且结构简单易实现。早期的粒子群算法收敛速度快，可能导致在收敛过程中错过最优解，也可能出现粒子趋同的现象，导致粒子的多样性减少，使算法优化到一定程度无法继续。随后研究人员从以下几个方面对算法进行改进：(1)由于算法要设置的参数较少，因此参数的改进大多针对惯性权重和学习因子；(2)将粒子群算法与多种算法(比如进化、遗传等算法)混合使用来优化设计数字滤波器，使其取长补短达到更好的优化效果。

1.5.1 惯性权重的改进

粒子群算法最初由Kennedy等提出，SHI Y等[32]在粒子群算法中添加新的惯性权重，从而控制粒子的收敛速度，更新后的方程如下：

研究表明，惯性权重的调整对粒子群算法的性能有影响。惯性权重通过先前粒子的速度控制当前粒子的速度，从而调节粒子在全局搜索和局部搜索之间的矛盾。较大的惯性权重有利于加强全局搜索能力，而较小的惯性权重则有利于局部搜索，所以如何平衡两者之间的关系也是改进的难点之一。Pavani等将这种改进的算法与早期的粒子群算法，窗函数法以及频率采样法等，从通带、阻带增益以及执行时间等方面进行比较，都在一定程度上显示了引入惯性权重对于粒子群算法设计数字滤波器性能提升上的优势。

最初针对惯性权重的改进只是将其设为一个常数，为了进一步平衡局部搜索能力和全局搜索能力并跳出局部最优解，SHI Y等将w线性表示为：

其中，wmax是惯性权重的最大值，wmin是最小值，t为当前迭代次数，T为总体迭代次数。除此之外，陈贵敏等[33]提出其他三种改进惯性权重的策略：

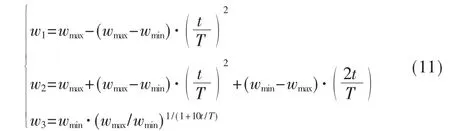
实际测试中第三种策略的收敛精度和收敛速度均优于其他两个。

改进惯性权重的相关研究包括：HUANG W P等[34]利用式(9)惯性权重粒子群算法代替频率采样法滤波器的设计，获得了最大阻带衰减，但是标准的粒子群算法容易陷入局部最优。李辉等[35]使用式(9)改进的粒子群算法优化数字滤波器参数过程中发现初始值的选取仅影响收敛速度。周飞红等[36]比较了惯性粒子群算法和Parks-McClellan(PM)两种方法设计高通数字滤波器，结果表明前者设计的数字滤波器阻带衰减更大，通带波动更小。

1.5.2 学习因子的改进

在早期的粒子群算法中将学习因子c1、c2设为常数，使得粒子自身认知能力和全局认知能力达到平衡，但是按照经验设计的常数学习因子滤波器的幅频响应与理想的频率响应有很大的误差。因此，也有学者在学习因子的改进上做了些研究工作。Clerc引入压缩因子来限制学习因子，另外还有学习因子同步变化、学习因子异步变化和三角函数学习因子法，以及惯性权值的学习因子的改进等，这些方法一定程度上提高了滤波器的设计性能。

1.5.3 粒子群算法的其他改进策略

传统粒子群算法的问题在于过早收敛和不稳定，已经有很多种克服了以上两种缺点的改进粒子群算法应用于FIR滤波器的设计中，其中包括反向学习(OPSO)粒子群算法、疯狂PSO(CRPSO)、混合算法(DEPSO)和混沌粒子群(CPSO)等。JEHAD I A等[37]使用粒子群算法和遗传算法设计了FIR数字滤波器，PSO参数设计比GA所需参数更为简单直观，此外文中的两个设计案例都显示粒子群算法可成功实现优化目标，而且收敛性优于遗传算法。SUN J等[38-39]根据粒子群的量子行为，提出新的量子粒子群算法模型，其全局搜索能力远远高于标准的粒子群算法。吕国等[40]将量子粒子群算法应用于数字滤波器设计中并且与标准粒子群算法比较，结果表明运算量相对减少，通带变宽，幅频响应更接近理想特性。梁慧等[41]将混沌搜索策略与粒子群优化算法相结合设计高通数字滤波器，与PM设计方法相比较，结果显示前者设计的滤波器通带波动小，阻带衰减大，收敛速度快。ZHAO Z等[42]分别将混沌粒子群算法与原始的粒子群算法和量子粒子群算法用于设计数字滤波器并分析对比，发现混沌粒子群算法能够以更少的时间收敛到全局最优。KAR R等[43]提出用基于疯狂度的粒子群算法优化设计数字滤波器，引入疯狂算子，确保粒子的多样性，改善易陷于局部最小值的问题。赵安新等[44]用综合学习粒子群算法改进频率采样法设计数字滤波器，节约了粒子在错误方向上花费的时间，解决粒子群算法易于陷入局部最优点的问题。KUMAR P U[45]等将PSO与传统算法相比，不仅改善阻带的衰减，而且利用了在不连续点附近对样本值进行插值，从而减少误差。AGGARWAL A[46]等研究了布谷鸟搜索算法、粒子群算法和遗传算法设计数字滤波器的性能对比，结果显示粒子群算法设计的结果在收敛速度，执行时间和幅度响应误差精度等方面都略逊于布谷鸟搜索算法，说明粒子群算法在设计数字滤波器的参数设计上还有待改进。SHAO P[47]等将基于折射相反学习模型改进的粒子群优化算法用于设计具有线性相位的FIR低通和高通数字滤波器，结果表明此方法设计数字滤波器的性能优于其他算法，此方法可以获得更快的收敛速度和更好的精度。

以上基于智能算法设计滤波器的性能基本集中在通带和阻带波纹，表1从滤波器的阶数(Order)、最大阻带衰减(Maximum stop band attenuation)、最大通带波纹(Maximum pass band ripple)、最大阻带波纹(Maximum stop band ripple)和过渡带宽(Transition Width)五个方面对多种设计算法进行分析对比，结果显示改进后的粒子群算法、进化算法在通带衰减和阻带波纹方面都显示其优越性。

表1 多种算法设计FIR滤波器参数比较

2 结论

本文对FIR数字滤波器设计常用的几种典型启发式优化算法进行综述。将滤波器的设计问题转化为多参数优化，通过使用不同的优化技术让误差函数最小，从而确定滤波器系数。上文就经典方法和智能算法分开进行阐述，发现了智能算法在设计时间和准确度等方面比传统的设计技术更优越。

对于复杂的优化问题使用遗传算法、粒子群算法和差分进化等智能算法求解，由于智能算法求解是随机搜索的过程，可能使得每一次的运行结果，收敛曲线都有一定的不同，在数字滤波器的设计过程中一般认为幅频响应或单位脉冲响应收敛于一个固定值时，该固定值就是此次运算的最优解，所以判断哪一次运行结果是最优值，参考文献中提出大概两种方法：(1)多运行几次对比；(2)统计计算的每次结果分析平均值或方差等进行判断。另外误差函数是个很好的性能指标判断条件，但是也不是适用于所有滤波器的通用标准。

几种经典算法中，虽然遗传算法使用率最高，但是从文章的分析可以看出，遗传算法由于设计滤波器时参数比粒子群算法和差分进化算法都相对复杂，所以如何降低计算复杂度，同时又能保证滤波器性能是继续努力的方向。虽然采用粒子群算法和差分进化算法设计数字滤波器一直表现出良好的效果，但是实际应用方面距离理论设计还是有一定的差距，所以实际应用紧跟理论研究也是今后继续努力的方向。