典型优化目标函数下源参数反演性能对比研究
胡 峰,郎建垒,毛书帅,玄博元
典型优化目标函数下源参数反演性能对比研究
胡 峰,郎建垒*,毛书帅,玄博元
(北京工业大学环境与生命学部,区域大气复合污染防治北京市重点实验室,北京 100124)
基于外场实验数据,从反演高估率、准确性、稳定性角度系统评估了8种典型目标函数在不同未知源参数反演情形下的反演性能差异.研究发现,不同目标函数反演性能差异显著.仅反演单参数源强时(),对数变换目标函数高估率最大(79.4%),偏差平方和目标函数准确性最高(ARD<50%=82.3%,ARD=(35.3±9.1)%),目标函数稳定性无明显差异(CV<0.01).三参数反演(,,)时,标准化均方根误差目标函数源强高估率最大(98.5%),对数变换目标函数准确性、稳定性最高(ARD<50%=91.1%,ARD=(48.4±9.8)%;CV=0.01);位置方面,偏差平方和目标函数准确性最高(AD=(36.12±11.39)m),对数变换目标函数稳定性最强(CV=0.0018).四参数反演(,,,)时,标准化均方根误差目标函数源强高估率最大(98.5%),对数变换目标函数准确性、稳定性最优(ARD<50%=61.7%,ARD=(55.2±16.5)%;CV=0.03);位置方面,相关系数总体表现最优(AD=(34.37±10.72)m; CV=0.011).整体上,随反演参数变化,对数变换目标函数源强反演性能最稳定.
源参数反演;突发大气污染事故;高斯烟羽模型;启发式算法;目标函数
快速、准确识别污染源参数(源强、位置)对科学、有效开展大气污染事故应急处置工作具有重要意义.源参数反演技术是确定事故源信息的重要手段.目前,国内外已经开展了大量研究.如张建文等[1]将遗传-单纯形耦合算法(GA-NM)用于位置和源强参数反演,显著提升了源反演性能;Cui等[2]提出将粒子群-单纯形耦合算法(PSO-NM)用于研究不同大气扩散条件对源反演的影响;沈泽亚等[3]对比了3种耦合算法(PSO-NM、GA-NM和GA-PSO)反演性能,毛书帅等[4]比较了不同源排放情形下标准算法(PSO、GA)和耦合算法(PSO-NM)反演性能.然而,上述研究集中于优化算法在源反演中的应用或不同算法性能对比研究.目标函数的构建是源反演技术建立的重要一环.目前,在以算法应用及改善为主的源反演研究中,大多以偏差平方和目标函数建立源反演技术,并开展研究[5-7];文献[8-9]建立了对数变换目标函数分别探究了传感器阈值及数量对反演效果的影响;Annunzio等[10]使用浓度贡献率目标函数探究多点源反演问题;文献[11-12]分别基于模拟案例、单次外场草原实验数据[13]比较不同目标函数的源参数反演效果,发现不同目标函数下的源反演差异影响显著.
然而,真实突发大气污染事故情景复杂,可能出现不同的源参数反演情景,如火灾情形,通常事故源位置已知,该情形可归为源强未知的单维参数线性反演问题;对于泄漏事故,由于泄漏物质可能无色、无味,具有一定的隐蔽性,往往无法预知泄露源的位置、源强等信息,此时可归为多维参数非线性反演问题[4,7,14].而上述研究主要以模拟事故案例或单次外场实验案例研究为主,且未考虑不同情景下目标函数选择对源反演的影响.因此,本文基于68次美国草原SO2泄漏模拟实验数据集[13],开展了不同源参数数量反演情形下8种典型目标函数反演效果对比研究,从反演高估率、准确性、稳定性角度系统评估了典型目标函数在不同未知源参数反演情形下的源反演性能差异.本研究结果有助于理解不同目标函数在解决线性与非线性优化源反演问题的性能差异,可为多种事故情景下污染源信息(源强、位置)的准确估算提供科学依据.
1 材料和方法
1.1 实验数据
美国草原SO2泄漏实验[13]在美国内布拉斯加州奥尼尔镇东北部草原地区(42°29.6¢N,98°34.3¢E),平均海拔600余米.SO2草原释放实验包括68次外场释放实验,其中大气稳定度A下开展了5次实验,大气稳定度B下开展了5次实验,大气稳定度C下开展了10次试验,大气稳定度D下开展了31次实验,大气稳定度E下开展了5次实验,以及大气稳定度F下开展了12次试验.此外,在美国SO2草原释放实验中,1~65次实验的气体释放高度为距离地面0.46m,66~68次实验的气体释放高度为距离地面1.5m,单次实验释放时间为10min.下风向布点采用半圆弧布点方式,共计布设5层采样点,各层布点覆盖范围均为180°,分布半径分别为50, 100, 200, 400和800m,其中前4层采样点按照每间隔1°进行布设,每一层采样弧段共计180个采样点,第5层采样点按照每间隔2°进行布设,共计90个采样点,采样高度距地面1.5m.本文采用距离地面2m处测得的气象信息(风速、风向),所有外场实验相关信息参考文献[15].
1.2 高斯烟羽模型

表1 BRRIGS 扩散参数方案(平坦开阔地形)
注:、分别为水平和垂直方向的扩散参数,单位m;0、分别为释放点和采样点的横坐标,单位m.
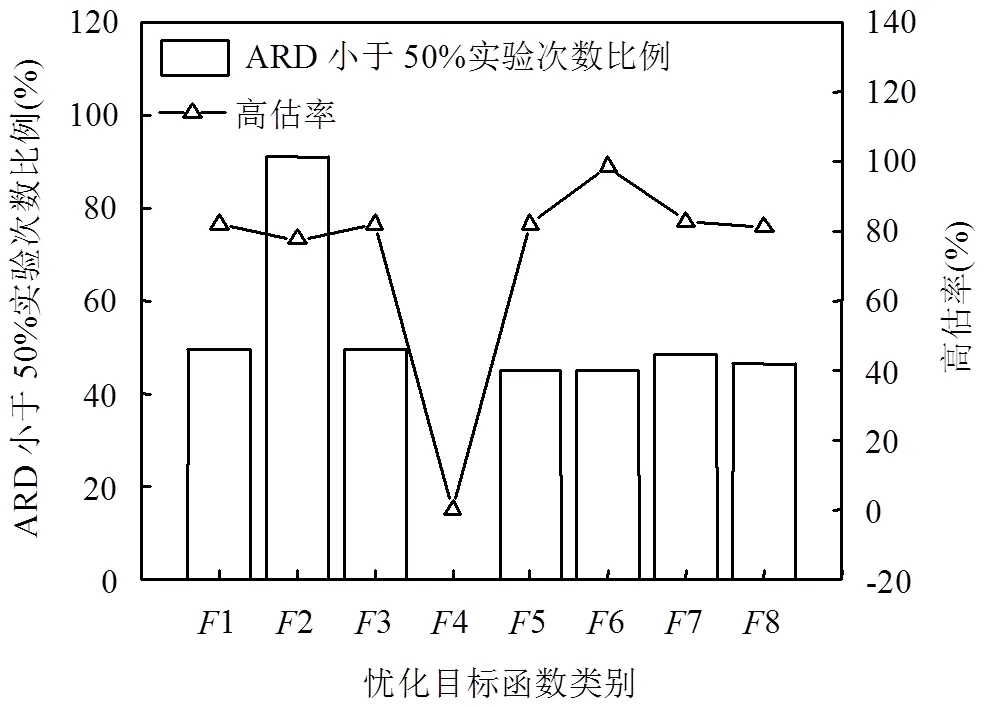
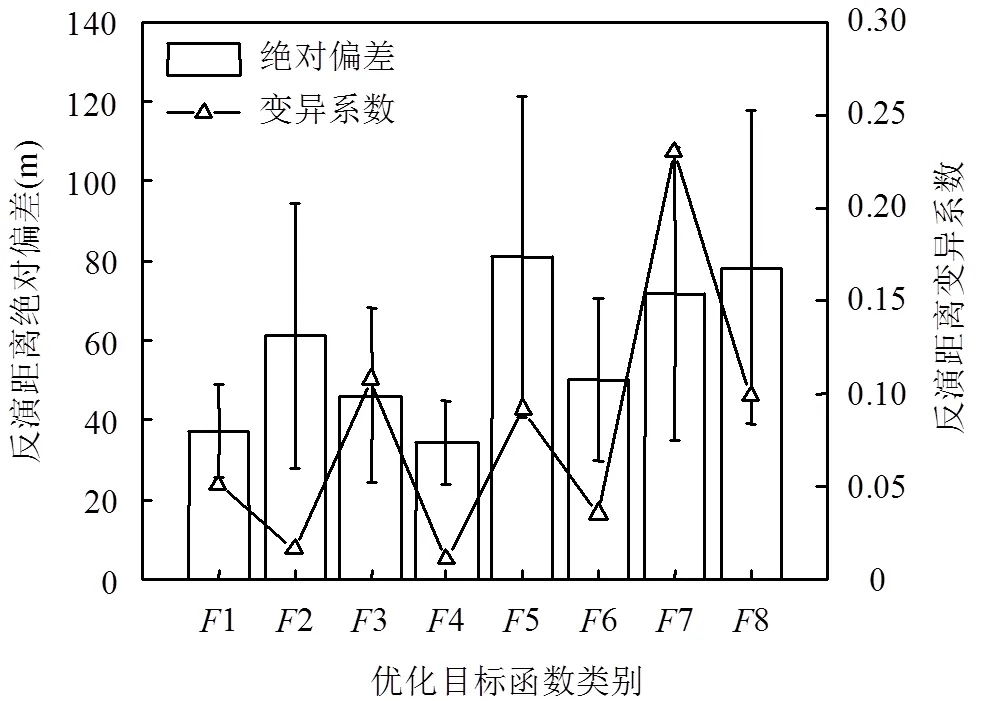
高斯烟羽模型是基于理想假设而推导出的气体扩散模式[16],常用于平坦开阔地形下稳态流场的模拟.本研究中采用的实验数据为草原污染释放示踪实验数据,且实验数据集为10min采样时间的污染浓度均值[15],因此,可认为地形平坦开阔且流场相对稳定.文献[17]指出,当模型指标如分数偏差(FB)、归一化均方误差(NMSE)满足:-0.3 式中:0为释放源强, g/s;为平均风速, m/s; σ和σ分别为水平和垂直方向的扩散参数,本文采用BRRIGS扩散参数方案[19](表1);(,,)为下风向对应监测点在(,,)位置处的污染物模拟浓度, g/m3; (0,0,0)为事故源的位置参数,其中(0,0)为事故源的平面坐标,0为事故源有效释放高度, m. 由于启发式算法具有对初值依赖性低等优点,近年来被广泛运用于污染物溯源问题中[1-7,20-22].标准遗传算法(GA)[1,7,9]、标准粒子群算法(PSO)[2-3]和人群搜索算法(SOA)是3种典型的启发式算法.GA是模拟自然界生物进化过程的计算模型[23],经过选择、交叉和变异3种基本遗传操作,逼近问题最优解. PSO的思想源于自然界鸟群捕食过程,通过群体协作找到问题的全局最优解[24]. SOA研究人类在随机搜索时所采用的交流、协作、记忆、推理、学习知识与经验等的智能行为,结合搜索和进化思想,以搜寻队伍为种群,以搜寻者位置为优化问题的候选解,通过模拟人类搜索的“经验梯度”和不确定性推理,分别确定搜索方向和步长,完成位置更新,实现对所求问题解的优化[25].本研究通过对3种启发式算法进行对比评估,筛选出极小值寻优性能最好的算法,并将其作为源参数反演算法. 目标函数是评价优化性能指标的数学表达式.在源参数反演问题中,利用启发式算法寻找正向扩散模式的模拟浓度与监测浓度的最优匹配,并通过优化目标函数来定义.参照已有的研究成果[26-29],构建下列目标函数: Function 1 (1):基于浓度偏差平方和形式的目标函数: 式中:代表高斯烟羽模型的模拟浓度值,代表监测浓度.表示采样点总数,表示第个观测点,C为扩散模型在第点的浓度计算值, g/m3;O为第点的实际监测值, g/m3,下同. Function 2 (2):基于对数变换形式的浓度均方根误差目标函数: 式中:为常数,用于保证aC和aO均大于1. Function 3 (3):基于浓度贡献率形式的目标函数: Function 4 (4):基于相关系数形式的目标函数: 式中:σ和σ分别为模拟浓度()和监测浓度()的标准差. Function 5 (5):基于浓度分数偏差绝对值形式的目标函数: Function 6 (6):基于浓度标准化均方根误差形式的目标函数: Function 8 (8复合目标函数,Wade等[30]使用该目标函数确定多点源反演问题中释放源的数量,具体如下: 式中: FAC2∈[0.5,2],表示模拟浓度和监测浓度比的模拟数据占所有数据的比值; AFB表示模拟浓度与监测浓度分数偏差的绝对值,表达式与5相同;表示模拟浓度和监测浓度的相关系数. 在仅反演源强()的情形下,事故源的位置信息(,,)是已知的,构建如下优化模型以及相应源参数约束条件: 在三参数反演情形下,源强()和位置(,)是未知的,此种情形下是将事故源简化为地面源,此时优化模型及源参数约束条件可表示为: 在四参数反演情形下,源强()和位置(,,)是未知信息,此时优化模型及源参数约束条件可表示为: 上式中,Function代表优化目标函数.使用启发式算法反演源参数的具体过程如下所示: (1)初始化:确定待反演源参数数量,种群中的所有个体都包括相应的源参数,构成对应源参数的优化搜索. (2)将初始群体以及气象数据(包括风速、大气稳定度等)代入扩散模型(高斯烟羽模型),得到各采样点的模拟浓度,并与监测浓度作对比,即通过优化目标函数(参照公式(2)~(9))计算个体适应值; (3)由个体适应值比较获得群体的最优适应值并作纪录; (4)根据上述优化模型(参照公式(10)~(12)),按照特定的进化规则,进行种群的更新,直到满足迭代停止标准.输出具有最优适应度值的源参数最优解. 在实际应急处置中,源强反演结果在一定程度上高于真实值可能更适用于计算安全距离和确定应急疏散区域[31],故本研究使用高估率(overestimated)比较不同目标函数对于68次实验反演结果的高估情况,高估率为源强反演结果高于真实值的实验数 (overestimated)占全部实验(all)的比重;使用反演源强相对偏差绝对值(ARD)小于50%的实验次数(ARD<50%)占全部实验次数(all)的比重指标(ARD<50%)、反演位置偏差的绝对值(AD),用以表征不同目标函数源参数反演结果的准确性;利用变异系数(CV)来评估不同目标函数在反演中的稳定性,其中变异系数越小,稳定性越强,变异系数越大,则稳定性越弱[31],具体表达式为: (15)~(16)式中:代表反演值,代表真实值,代表测试实验序号,代表源强, g/s;代表反演源与真实源的距离, m. (17)式中,代表每次实验源强或距离反演结果偏差(ARD或AD)的标准差,代表每次实验源强或距离反演结果偏差(ARD或AD)的平均值.对于距离,在三参数反演情形下(高度已知,,,未知),其中r=r=0m,其表达式为: 四参数反演情形下(,,,均未知),其中, r=r=0m, r=0.46或1.5m,其表达式为: 研究发现[3,6],不同算法的源参数反演性能有较大差异.为选择优化性能相对较好的算法进行源参数反演,本文采用Sphere、Schaffer和Rastrigin经典函数分别对GA、PSO和SOA三种算法进行极小值寻优性能对比实验,各经典函数的表达式、搜索范围、理论极小值和峰值情况具体参照文献[32],具体的优化结果见表2. 表2 不同经典函数优化结果比较 如表2所示,通过3种算法(GA、PSO和SOA)对经典函数Sphere、Schaffer和Rastrigin的优化结果来判断(平均最优值、标准差以及优化结果的最大值、最小值),SOA 算法的极小值寻优性能要比GA和PSO更好.综合上述3种启发式算法对经典函数Sphere、Schaffer和Rastrigin优化结果.可以看出,人群搜索算法(SOA)完成函数优化分析具有收敛精度高、稳定性较好等特点.综上所述,采用人群搜索算法(SOA)作为源参数反演算法. 图1展示了仅反演源强情形下,不同目标函数68次SO2释放实验源强反演准确性(相对偏差绝对值,ARD)、稳定性(变异系数,CV)和高估率(overestimated).从高估率来看,2目标函数高估率最大(79.4%),其次为7(70.5%),最低为4(0.0%).这表明,在仅反演源强情形下,使用2目标函数进行源强反演时,出现高估现象的可能性更大.从准确性来看,仅反演源强情形下,1目标函数ARD<50%最高(82.3%),同时1源强反演结果ARD及其置信区间最低((35.3±9.1)%).这表明,1目标函数源强反演结果最为准确.从稳定性来看,各目标函数无明显差异(CV<0.01).综上所述,仅反演源强情形下,浓度偏差平方和目标函数(1)源强反演结果最为准确,稳定性较好,同时ARD<50%最高,但会低估部分实验源强(overestimated=58.4%),而此时对数变换目标函数(2)出现低估现象的实验次数最少. 2.3.1 源强反演性能分析 图2展示三参数情形下不同目标函数68次SO2释放实验源强反演准确性(ARD)、稳定性(CV)和高估率(overestimated).从高估率来看,6的高估率最大(98.5%),4最低(0%).这表明,使用6目标函数进行源强反演时,出现高估现象的可能性更大.从准确性来看,2目标函数ARD<50%最高(91.1%);2的源强反演结果ARD及其置信区间最低((48.4±9.8)%),其次为8((73.1±19.2)%),最高为3((104.9±35.9)%),这表明,在三参数反演情形下,2的准确性要明显优于其他目标函数.从稳定性来看,2目标函数演稳定性最强 (CV=0.01),4最高(CV=0.17).综上所述,在三参数反演情形下,对数变换目标函数(2)源强反演结果准确性、稳定性均表现最优,这可能是由于目标函数2表达式中对观测值和模拟值均取对数,从而使得源参数反演结果受极高或极低值的影响更小有关. 2.3.2 位置反演性能分析 图3展示了在三参数情形下,不同目标函数68次SO2释放实验位置反演结果准确性(绝对偏差,AD)、稳定性(CV).从准确性来看,在三参数情形下,1目标函数的AD最小((36.12±11.39)m),4次之((39.37±10.82) m),5最大((73.88±37.09)m).这表明,1目标函数距离反演结果准确性要略优于4;从稳定性来看,2目标函数的变异系数最低(CV=0.0018),4次之(CV= 0.0021),7最高(CV=0.081).结果表明,在三参数反演情形下,偏差平方和目标函数(1)距离反演准确性最高,对数变换目标函数(2)稳定性最强,而分数偏差绝对值目标函数(5)准确性最低;平权复合目标函数(7)稳定性最低. 图3 三参数情形下不同目标函数位置反演性能对比 2.4.1 源强反演性能分析 图4展示了在四参数情形下,不同目标函数68次SO2释放实验源强反演性能.从高估率来看,6目标函数高估率最大(98.5%),这表明,使用标准化均方根误差目标函数(6)时,源强反演结果存在普遍高估的现象.从准确性来看,对数变换目标函数2源强反演结果准确性最高(ARD<50%=61.7%, ARD=(55.2±16.5)%),而浓度贡献率目标函数(3)源强反演结果与真值相差最大,这可能是因为,与其他目标函数相比,3目标函数更易受到极高或极低监测值的影响[11,17].从稳定性来看,2目标函数变异系数最低(CV=0.03),而其余目标函数变异系数均高于0.11,这表明,在四参数反演情形下对数变换目标函数(2)源强反演稳定性要明显优于其他目标函数.整体上,2目标函数在源强反演准确性和稳定性方面均表现最优,这与三参数反演情形结论一致. 如图5所示,从准确性来看,随着反演参数数量的变化,2目标函数ARD和ARD<50%要更加稳定;高估率方面,2、4目标函数的高估率无明显变化,这说明2、4目标函数的高估率受其反演参数数量变化影响较小,其中4目标函数的源强反演性能较差,这可能是由于使用相关系数目标函数,同时对源强和位置参数进行反演时,受目标函数自身结构影响,算法对源强参数的寻优有更强的随机性有关[33].从稳定性来看,对数变换目标函数(2)源强反演性能最为稳定,该函数变异系数值始终处于较低水平,且受反演参数数量影响较小. 2.4.2 位置反演性能分析 图6展示了在四参数情形下,不同目标函数68次SO2释放实验位置反演结果准确性(AD)、稳定性(CV).从准确性来看,F4目标函数平均反演距离偏差绝对值AD最小((34.37±10.72)m),1次之((37.19±11.57)m),5最高((81.23±40.15)m).这表明,在四参数反演情形下,不同目标函数对于位置反演效果差异明显,其中4目标函数位置反演结果准确性最高.从稳定性来看,4目标函数的变异系数最小(CV=0.011),其次为2(CV=0.016),7最大(CV=0.23).这表明,相关系数目标函数(4)位置反演结果稳定性最高.综上所述,在四参数情形下,相关系数目标函数(4)位置反演性能总体表现最优. 图5 不同目标函数源强反演性能随参数数量变化情况 图6 四参数情形下不同目标函数位置反演性能对比 本研究结果可提高人们对不同优化目标函数下源参数反演性能差异的认知,可为突发事故源参数反演目标函数的合理选择提供科学依据,此外,不同目标函数反演高估率分析结果可为应急处置中安全距离和应急疏散区域的确定提供参考,提升应急管理部门突发大气污染事故应急响应能力. 3.1 从高估率来看(仅源强而言),单参数情形下,对数变换目标函数最高(单参数:79.4%);在三参数、四参数情形下,标准化均方根误差目标函数最高(98.5%). 3.2 从准确性来看,就源强而言,单参数情形下,偏差平方和目标函数(1)准确性最高(单参数:ARD<50%=82.3%,ARD=(35.3±9.1)%;在三参数和四参数情形下,对数变换目标函数(2)准确性总体最优(三参数:ARD<50%=91.1%,ARD=(48.4±9.8)%;四参数:ARD<50%=61.7%,ARD=(55.2±16.5)%);综合来看,对数变换目标函数准确性受反演参数数量变化影响较小.就位置而言,三参数情形下,偏差平方和目标函数(1)准确性最高(AD=(36.12±11.39)m);四参数情形下,相关系数目标函数(4)准确性最高(AD= (34.37±10.72)m). 3.3 从稳定性来看,就源强而言,单参数情形下,各目标函数稳定性无明显差异(CV<0.01);三参数和四参数情形下,对数变换目标函数(2)稳定性最优(三参数:CV=0.01;四参数:CV=0.03).就位置而言,三参数情形下,对数变换目标函数(2)稳定性最强(CV=0.0018);四参数情形下,相关系数目标函数(4)稳定性最强(CV=0.011). [1] 张建文,王煜薇,郑小平,等.基于混合遗传-Nelder Mead单纯形算法的源强及位置反算 [J]. 系统工程理论与实践, 2011,31(8):1581- 1587. Zhang J W, Wang L W, Zheng X P, et al. Back-calculation of source strength and position by a hybrid genetic-Nelder Mead simple algorithm [J]. Systems Engineering Theory and Practice, 2011,31(8): 1581-1587. [2] Cui J, Lang J, Chen T, et al. Investigating the impacts of atmospheric diffusion conditions on source parameter identification based on an optimized inverse modelling method [J]. Atmospheric Environment, 2019,205(5):19-29. [3] 沈泽亚,郎建垒,程水源,等.典型耦合优化算法在源项反演中的对比研究 [J]. 中国环境科学, 2019,39(8):3207-3214. Shen Z Y, Lang J L, Cheng S Y, et al. Comparative and study on the application of typical hybrid algorithms in source parameter inversions [J]. China Environmental Science, 2019,39(8):3207-3214. [4] 毛书帅,郎建垒,陈 添,等.多情景源排放参数反演下典型优化算法性能对比 [J]. 北京工业大学学报, 2020,46(4):45-52. Mao S S, Lang J L, Chen T, et al. Performance of typical optimization algorithms on inversing multi-scene source parameters [J]. Journal of Beijing University of Technology, 2020,46(4):45-52. [5] 张久凤.基于监测数据的源强反算算法研究及应用 [D]. 北京:中国石油大学, 2011. Zhang J F. Study and application of source intensity back-calculation algorithm based on monitoring data [D]. Beijing:China University of Petroleum, 2011. [6] Ma D, Gao J, Zhang Z, et al. An improved firefly algorithm for gas emission source parameter estimation in atmosphere [J]. IEEE Access, 2019,7(99):111923-111930. [7] Mao S, Lang J, Chen T, et al. Impacts of typical atmospheric dispersion schemes on source inversion [J]. Atmospheric Environment, 2020,232(7):117572. [8] Rodriguez L M, Haupt S E, Young G S. Impact of sensor characteristics on source characterization for dispersion modeling [J]. Measurement, 2011,44(5):802-814. [9] Long K J, Haupt S E, Young G S. Assessing sensitivity of source term estimation [J]. Atmospheric Environment, 2010,44(12):1558-1567. [10] Annunzio A J, Young G S, Haupt S E. A multi-entity field approximation to determine the source location of multiple atmospheric contaminant releases [J]. Atmospheric Environment, 2012,62(12):593-604. [11] Cervone G, Franzese R. Monte Carlo source detection of atmospheric emissions and error functions analysis [J]. Computers & Geosciences, 2010,36(7):902-909. [12] Ma D, Deng J, Zhang Z. Comparison and improvements of optimization methods for gas emission source identification [J]. Atmospheric Environment, 2013,81(12):188-198. [13] Barad M L. Project prairie grass: A field program in diffusion: AF-152572 [R]. Geophysical Research Air Force Cambridge Research Laboratories, Bedford, 1958. [14] Ma D, Tan W. Parameter identification for continuous point emission source based on Tikhonov regularization method coupled with particle swarm optimization algorithm [J]. Journal of Hazardous Materials, 2017,325(5):239-250. [15] Cervone G, Franzese P. Non-Darwinian evolution for the source detection of atmospheric releases [J]. Atmospheric Environment, 2011,45(26):4497-4506. [16] HJ 2.2-2018 环境影响评价技术导则大气环境 [S]. HJ 2.2-2018 Technical guidelines for environmental impact assessment atmospheric environment [S]. [17] Chang J C, Hanna S R. Air quality model performance evaluation [J]. Meteorology & Atmospheric Physics, 2004,87(1-3):167-196. [18] Mao S, Lang J, Chen T, et al. Comparison of the impacts of empirical power-law dispersion schemes on simulations of pollutant dispersion during different atmospheric conditions [J]. Atmospheric Environment, 2020,224(3):117317. [19] Briggs G A. Diffusion estimation for small emissions: TID-28289 [R]. National Oceanic and Atmospheric Administration, Oak Ridge, Tenn. USA, 1973. [20] 曹宏桂,贠卫国.基于PSO-DE算法的突发水域污染溯源研究 [J]. 中国环境科学, 2017,37(10):3807-3812. Cao H G, Yun W G. Research of the abrupt waters pollution source based on optimization algorithm of PSO-DE [J]. China Environmental Science,2017,37(10):3807-3812. [21] 张双圣,强 静,刘汉湖,等.基于贝叶斯公式的地下水污染源识别 [J]. 中国环境科学, 2019,39(4):1568-1578. Zhang S S, Qiang J, Liu H H, et al. Identification of groundwater pollution sources based on Bayes’ theorem [J]. China Environmental Science,2019,39(4):1568-1578. [22] 潘紫东,卢文喜,范 越,等.基于模拟-优化方法的地下水污染源溯源辨识 [J]. 中国环境科学, 2020,40(4):1698-1705. Pan Z D, Lu W X, Fan Y, et al. Inverse Identification of groundwater pollution source based on simulation-optimization approach [J]. China Environmental Science,2020,40(4):1698-1705. [23] 唐穗欣.标准遗传算法的原理及算例[J]. 软件导刊, 2007,6(1):99- 101. Tang S X. Principle and example of standard genetic algorithm [J]. Software Guide, 2007,6(1):99-101. [24] 张丽平,俞欢军,陈德钊,等.粒子群优化算法的分析与改进[J]. 信息与控制, 2004,33(5):513-517. Zhang L P, Yu H J, Chen D Z, et al. Analysis and improvement of particle swarm optimization algorithm [J]. Information and Control, 2004,33(5):513-517. [25] Dai C, Chen W, Zhu Y, et al. Seeker Optimization algorithm for optimal reactive power dispatch [J]. IEEE Transactions on Power Systems, 2009,24(3):1218-1231. [26] Allen C T, Young G S, Haupt S E. Improving pollutant source characterization by better estimating wind direction with a genetic algorithm [J]. Atmospheric Environment, 2007,41(11):2283-2289. [27] 吉志龙.基于遗传算法的气载核素大气扩散反演模型研究 [D]. 上海:上海交通大学, 2014. Ji Z L. Study on back calculation of airborne radionuclides dispersion with genetic algorithm [D]. Shanghai:Shanghai Jiao Tong University, 2014. [28] 董吉开,杜文莉,王 冰,等.湍流状态下化学品扩散溯源中不同目标函数的影响分析 [J]. 化工学报, 2020,71(3):1163-1173. Dong J K, Du W L, Wang B, et al. Investigating impacts of cost functions to atmospheric dispersion modeling and source term estimation in turbulent condition [J]. Journal of Chemical Industry and Engineering, 2020,71(3):1163-1173. [29] 云慧敏,吴 锋,殷 勇,等.基于线性加权评价法的碟式斯特林机多目标优化 [J]. 武汉工程大学学报, 2020,42(2):218-223,230. Yun H M, Wu F, Yin Y, et al, Multi-objective optimization of dish stirling engine based on linear weighted evaluation function method [J]. Journal of Wuhan Institute of Technology, 2020,42(2):218-223, 230. [30] Wade D, Senocak I. Stochastic reconstruction of multiple source atmospheric contaminant dispersion events [J]. Atmospheric Environment, 2013,74(8):45-51. [31] 崔继宪.突发大气污染事故快速溯源与应急评估技术研究及验证 [D]. 北京:北京工业大学, 2019. Cui J X. Research and verification of rapid traceability and emergency assessment technology for sudden air pollution accidents [D]. Beijing:Beijing University of Technology, 2019. [32] 刘立群,韩俊英,代永强,等.果蝇优化算法优化性能对比研究 [J]. 计算机技术与发展, 2015,25(8):94-98. Liu L Q, Han J Y, Dai Y Q, et al. Comparative study on optimization performance of fruit fly optimization algorithm [J]. Computer Technology and Development, 2015,25(8):94-98. [33] Wang Y, Huang H, Huang L, et al. Source term estimation of hazardous material releases using hybrid genetic algorithm with composite cost functions [J]. Engineering Applications of Artificial Intelligence, 2018,75(10):102-113. Comparative study on source parameters inversion performance of typical cost functions. HU Feng, LANG Jian-lei*, MAO Shu-shuai, XUAN Bo-yuan (Key Laboratory of Beijing on Regional Air Pollution Control, Beijing University of Technology, Beijing 100124, China)., 2021,41(5):2081~2089 Based on Prairie grass experiments, the differences in inversion performance from eight typical cost functions were systematically evaluated with metrics of accuracy, robustness and overestimation rate. It was found that substantial differences in the inversion performance presented cross models with different cost functions. In terms of single unknown source parameter inversion (only for source strength ()), the cost function based on logarithm transformation scheme had the highest overestimation rate (79.4%), and that associated with the sum of deviation squares scheme exhibited the best accuracy(ARD<50%=82.3%, ARD=(35.3±9.1)%); while no significant difference (CV<0.01) was found in the robustness from different cost functions. In terms of three unknown source parameter inversion (source strength () and location (,)), the cost function based on normalized root mean square error scheme had the highest overestimation rate (98.5%) for source strength, the logarithm transformation cost function performed the best in the measure of accuracy and robustness (ARD<50%=91.1%, ARD=(48.4±9.8)%; CV=0.01); the cost function based on the sum of deviation squares scheme had the highest accuracy for the source location (AD=(36.12±11.39)m), while the logarithm transformation cost function showed the best robustness (CV=0.0018). In terms of four unknown source parameters inversion (source strength () and location (,,)), the cost function based on normalized root mean squared error exhibited the highest overestimation rate (98.5%) for source strength, and the logarithm transformation scheme got the best accuracy and robustness (ARD<50%=61.7%, ARD=(55.2±16.5)%; CV=0.03); the correlation coefficient scheme performed the best in accuracy and robustness for source location (AD=(34.37±10.72)m; CV=0.011). In general, the logarithm transformation cost function had the most stable inversion performance with the increase of the unknown source parameters. source parameters inversion;sudden air pollution accidents;gaussian dispersion model;heuristic algorithm;cost function X511 A 1000-6923(2021)05-2081-09 胡 峰(1996-),男,安徽合肥人,北京工业大学硕士研究生,主要从事环境规划管理与大气污染防治方面的研究.发表论文4篇. 2020-10-06 国家重点研发计划(2017YFC0209905) * 责任作者, 副教授, jllang@bjut.edu.cn
1.3 启发式算法
1.4 源参数反演模型构建
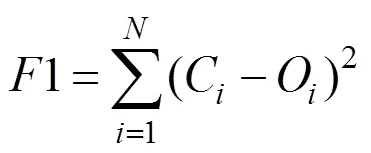





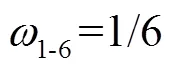
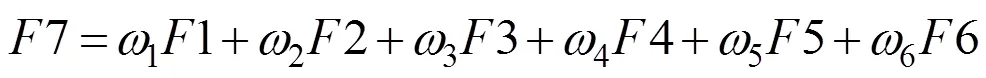

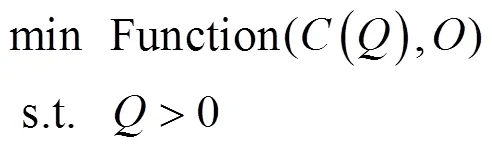
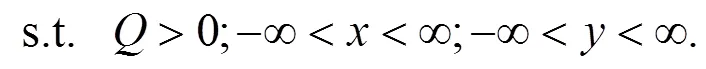
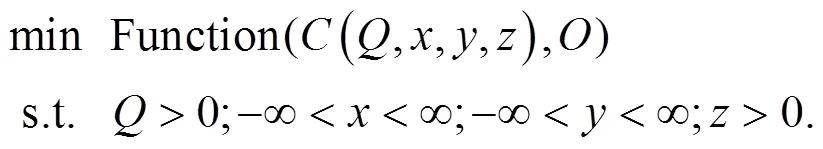
1.5 评估方法
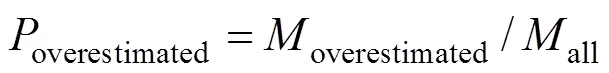
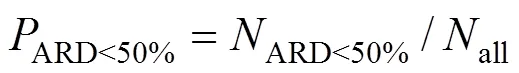


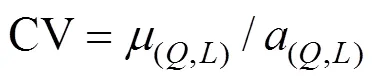

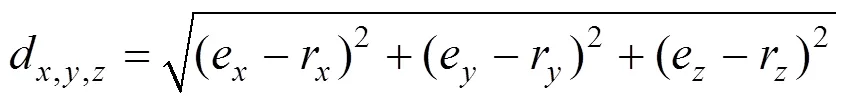
2 结果与讨论
2.1 算法优化性能对比

2.2 仅反演源强情形

2.3 三参数反演情形

2.4 四参数反演情形


3 结论

