BP-Adaboost 集成学习算法在地铁施工沉降预测中的应用研究

付秋新

（中铁十八局集团第四工程有限公司，天津 300480）

1 引言

我国地铁工程进入蓬勃发展阶段，但由于地铁工程多建于繁华市区，施工地质条件复杂，地下管线密集，地铁工程周边建筑物、道路众多，这些地层条件的不确定性及周围环境的复杂性增加了地铁施工的难度和风险[1-2]。为此，在地铁施工中，利用信息化监测数据对容易发生事故的部位进行监测，根据数据的变化采取针对性的预防措施，可以有效减少地铁施工事故的发生[3-5]。

目前常用于地铁施工沉降预测的算法主要包括灰色模型法、概率神经网络法、反向传播（BP）神经网络法、时间函数法等[6-9]。但由于地铁工程所处周边环境复杂，地质土质分布不均，以及地下水径流等因素影响，导致地铁施工沉降并不一定完全随着时间的变化而有序改变，这使得灰色模型、时间函数模型等依据时间线建立线性模型预测沉降的方法并不适用于地铁工程。因此，本文选用具有较强并行结构和学习能力的、依据非线性模型预测结果的BP神经网络算法构建预测模型，同时结合Adaboost集成学习算法将多个BP网络组建成强分类器模型——BP-Adaboost集成学习预测算法，以满足地铁施工沉降预测需求。

2 BP-Adaboost 集成学习算法原理

2.1 BP 神经网络算法

BP神经网络算法是一种具有多层结构的（3层或大于3层）、无反馈的、层内无互连结构的前向网络[10]。BP神经网络的网络结构中包含输入层、输出层以及若干个隐含层，其各层之间依靠神经元进行连接，但是层内的神经元之间无连接。由于机器学习中的Sigmoid函数具有可微性和良好的容错性，以及可以将非线性放大的系数减小，所以BP神经网络一般将该函数作为传递函数[11]。图1为3层BP神经网络结构图，其中Li为输入层，Hi为隐含层、Oi为输出层，wi（i= 1，2，…，n） 为初始权值，bi（i= 1，2，…，n） 为初始偏差值（这里初始偏差值设为1）。

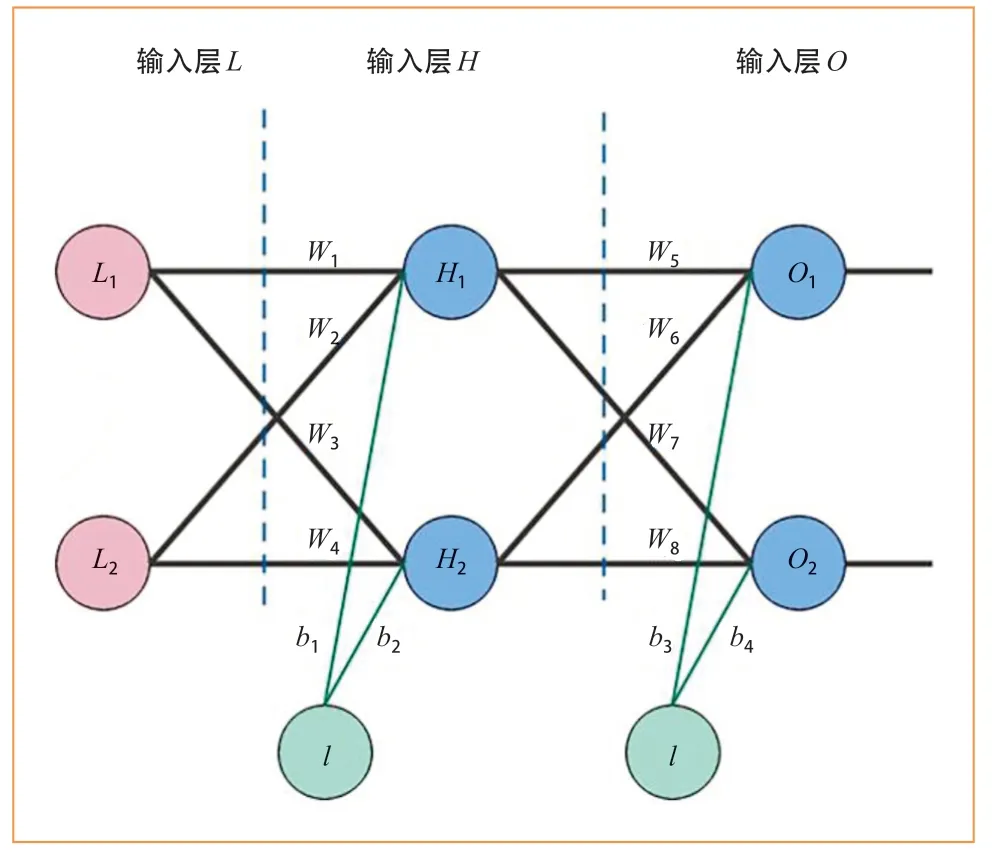
图1 BP神经网络结构图

BP神经网络算法采用的是误差反向传播算法，其原理为将1组已知目标输出的学习样本集传输到输入层、隐含层以及输出层中，并确定各层之间的初始权值和阈值。当输出值不满足期望输出时，则反向调整各层之间的权值和阈值，以减小误差，如此反复直到误差不再下降为止。最速下降法、动量最速下降法、拟牛顿法等都属于BP神经网络常用的学习算法，其区别在于修改权值时有不同的规则[12]。本文采用的对地铁施工地表沉降进行预测的BP神经网络算法属于最速下降法，所以下面以3层BP神经网络为例。

设含有一个BP神经网络，其传递函数为Sigmoid型函数（连续可微函数），网络中共L层和N个节点，传输信息是由每层节点接收，并传输给下一层节点。假设给定S个样本（xk，dk）（k= 1，2，...，S），即输入向量为xk（n维），网络的输出向量为dk（m维）[13-14]。当BP网络反向传播时，节点j的目标函数是该网络的期望输出djk与实际输出y，jk的误差平方EK，m为输出层的神经单元个数，即：

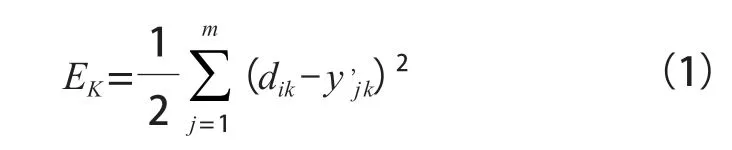
在BP网络传播时，需要通过调整权值w，使总误差E极小以获取最优解，权值调整公式如下：

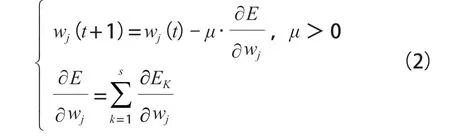
式（2）中，t为迭代次数；μ为步长；S为样本个数。

2.2 BP-Adaboost 集成学习算法

Adaboost算法是一种迭代方法，该算法首先建立一个初始模型，然后根据调整样本权重和弱分类器权值对初始模型进行错误修正[15]，以获取最优的弱分类器集合，其主要原理如下。

首先对数据进行划分、选择和网络初始化，D1为每次迭代的权重，w11为第一次迭代第一个样本权重，n为样本总数：

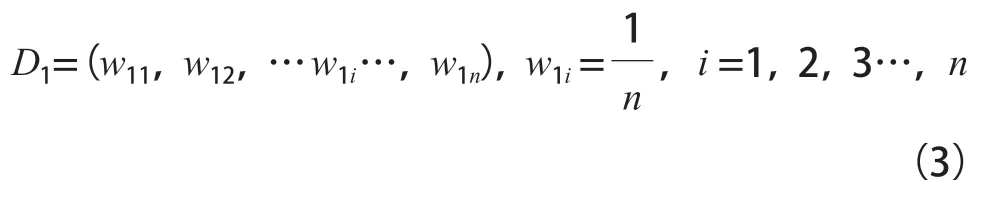
对训练数据生成n个BP神经网络弱分类器，根据分类器计算预测序列的权重ε：

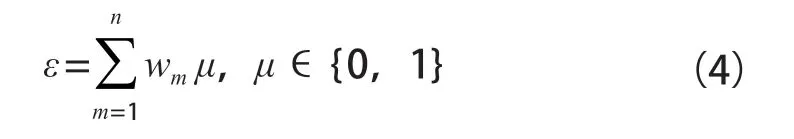
再对测试数据进行调整，然后根据式（5）生成强分类函数F（x），θm表示最终弱分类器的加权系数，fm（x）为第m个弱分类器：

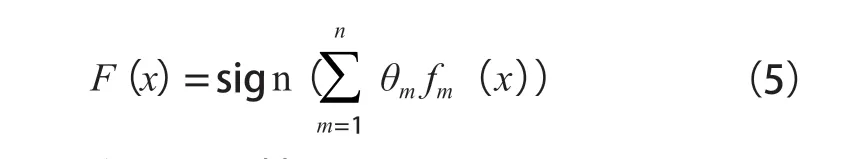
最终结果输出为G（x）：

式（6）中，1与-1表示不同类别的结果，最终根据生成的强分类函数得到最终的预测值。

3 地铁施工地表沉降预测

3.1 模型构建及样本数据获取

3.1.1 BP 神经网络算法构建

为避免数据质量与数量对模型训练产生不必要的干扰，在模型训练之前将数据正则化，选取的训练函数为Traingd函数[16]，传递函数选择Sigmid函数[17]，最大迭代次数设为1 000，学习设置为0.05，模型收敛误差设置为0.000 000 1。BP有1个输入层、5个隐含层和1个输出层。

3.1.2 灰色 GM（1，1）算法构建

GM（1，1）作为一种小样本线性预测模型，通过对系统主行为的特征量和关联因子建立灰色动态模型，以微分模拟法逐渐逼近真值进行预测[18]。本次灰色GM （1，1）算法通过Matlab2019 b软件实现，对原始建模数据构建紧邻均值序列以获取灰色GM（1，1）算法公式进行数据预测。

3.1.3 BP-Adaboost 集成学习算法构建

BP-Adaboost算法在BP神经网络基础上嵌入集成学习的内容，主要在权重初始化和BP神经网络分类器初步预测后，根据预测结果中的错误样本数error（v）反应预测结果准确性，然后通过错误样本数调整BP网络的权重q，将多个BP弱分类器构建为强分类器[19]，以sign函数计算强分类器结果，并分类统计强分类器的分类错误个数以选择最优解[20]。

BP神经网络本质是一种误差反向传播网络，其阈值和权重均在不断变化，所以每次网络训练的结果均有差异，因此，本文在经过多次反复训练之后，选取最优的1组数据作为最终结果参与分析。

3.1.4 样本数据获取

本文地铁施工地表沉降实验选取某地铁区间施工竖井工程，施工竖井支护结构为桩支护体系，基坑深19.088 m，作为盾构机吊出井。施工竖井周边设置有20个地表沉降测点DBC-01-01～DBC-01-20，本文选取DBC-01-10号测点在建设初期2019年8月1日— 2019年8月30日期间的30个地表沉降数据作为实验样本数据，并将前15 个数据用于训练模型，将后15个数据用于验证其可靠性。施工竖井地表沉降测点设置如图2所示，其中DBC-01-10号测点地表沉降数据见表1。

3.2 地表沉降预测结果及分析

利用Matlab分别完成灰色GM（1，1）算法、BP 神经网络算法、BP-Adaboost集成学习算法等3种算法，并以此对地表沉降进行预测分析，3种算法地表沉降预测数据与实测数据对比结果见表2。

由表2可知，3种算法中BP-Adaboost的相对误差最小，BP神经网络误差最大；从单点预测残差结果来看，灰色GM（1，1）算法最大残差为-2.620 4 mm，BP神经网络最大残差为3.474 7 mm，BP-Adaboost算法最大残差为0.744 5 mm。总体来看，基于BP神经网络改进的BP-Adaboost集成学习算法精度最佳，平均误差控制在0.4 mm以下。

根据GB 50911-2013《城市轨道交通工程检测技术规范》（简称《规范》）规定的中误差限差在0.6 mm以下要求，灰色GM（1，1）算法、BP神经网络算法的中误差均在1.1 mm以上，远高于该《规范》限差要求，BPAdaboost集成学习算法中误差为0.45 mm，满足该《规范》要求。

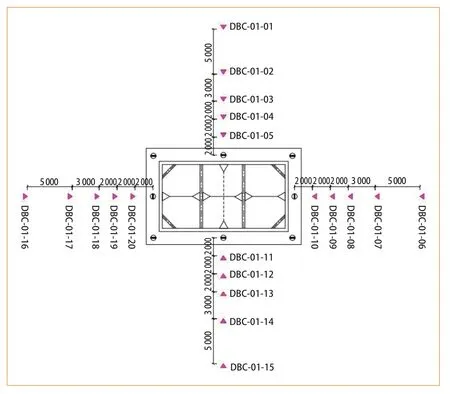
图2 施工竖井及地表沉降测点布置图（单位：mm）

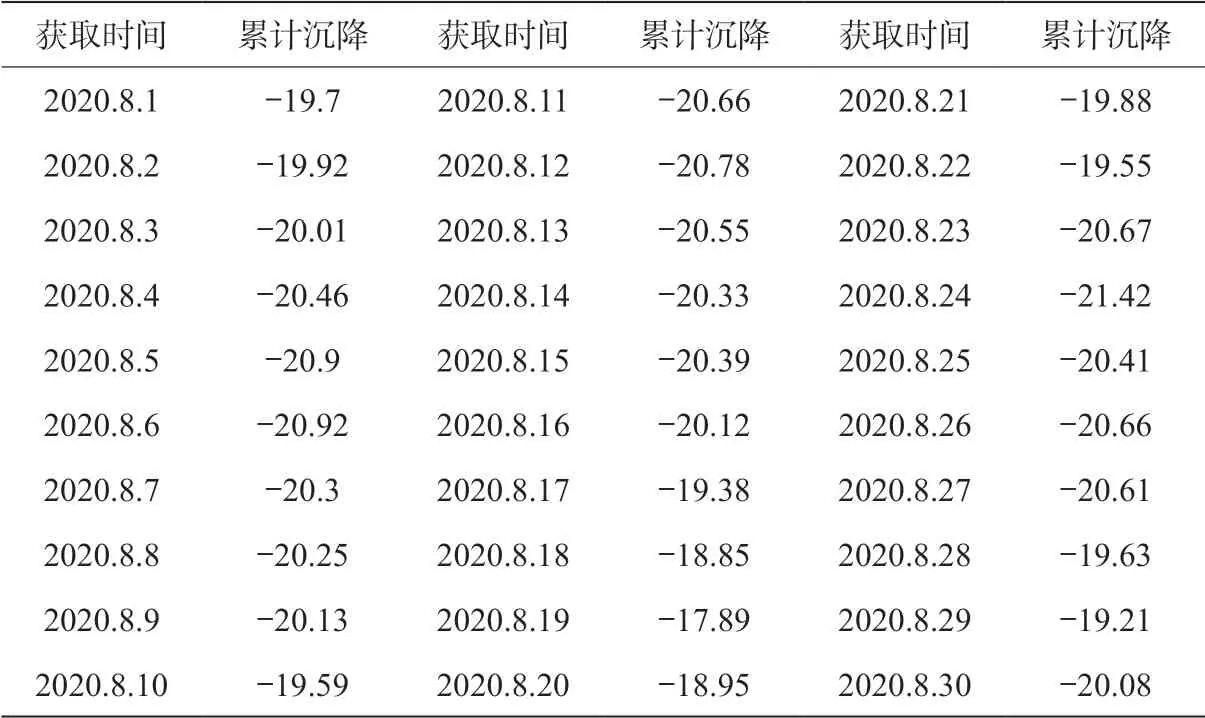
表1 DBC-01-10号测点地表沉降数据 mm

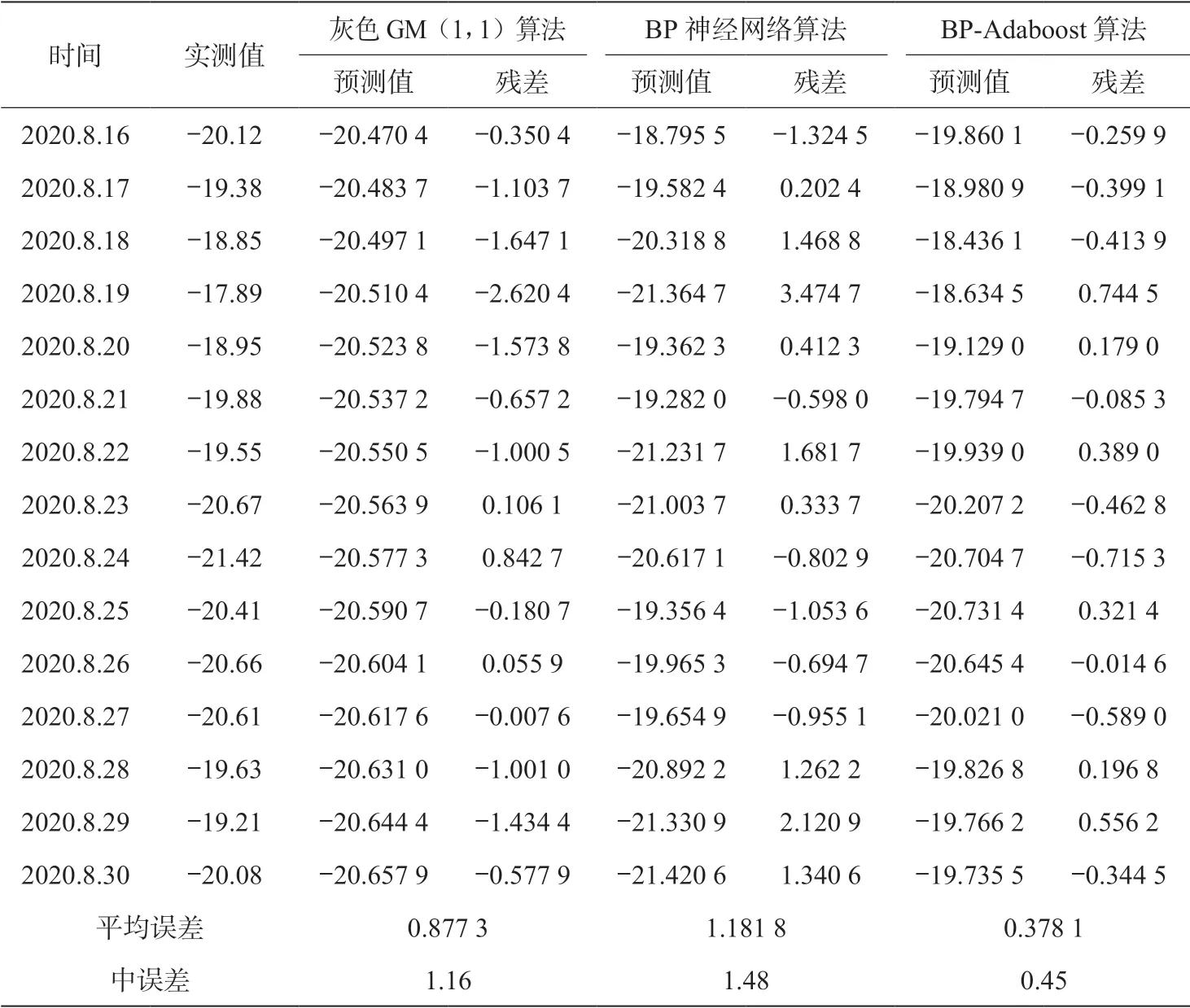
表2 3种算法预测地表沉降数据与实测数据对比 mm

为更直观显示3种算法预测数据与实测数据的真实拟合情况，通过样条曲线形式展示预测结果如图3所示。通过图3可以发现，灰色GM（1，1）算法本质上是一种线性预测模型，因此其对地铁施工地表沉降预测较差；BP神经网络由于本身属于个体学习算法，极易陷入局部极小状态，尤其当地铁施工沉降规律较为复杂时，算法的劣势更为突出；BP-Adaboost算法能够在未知函数模型的情况下，根据实测样本数据较好地预测地铁施工地表沉降，算法拟合度较高，可靠性较好。

4 结论

本文提出基于BP神经网络结合Adaboost算法的BP-Adaboost集成学习算法进行地铁施工沉降预测，并以某地铁施工竖井施工引起的地表沉降实测数据为样本数据进行地表沉降预测实验分析，实验分析结果表明，BP-Adaboost集成学习算法能较好地克服BP神经网络算法极易陷入局部极小的问题，其非线性预测的特点能够较好地预测复杂环境下的地铁施工沉降变化，较 BP神经网络算法、灰色GM（1，1）算法能更好地预测地铁施工地表沉降，为地铁施工沉降预测提供技术支持。

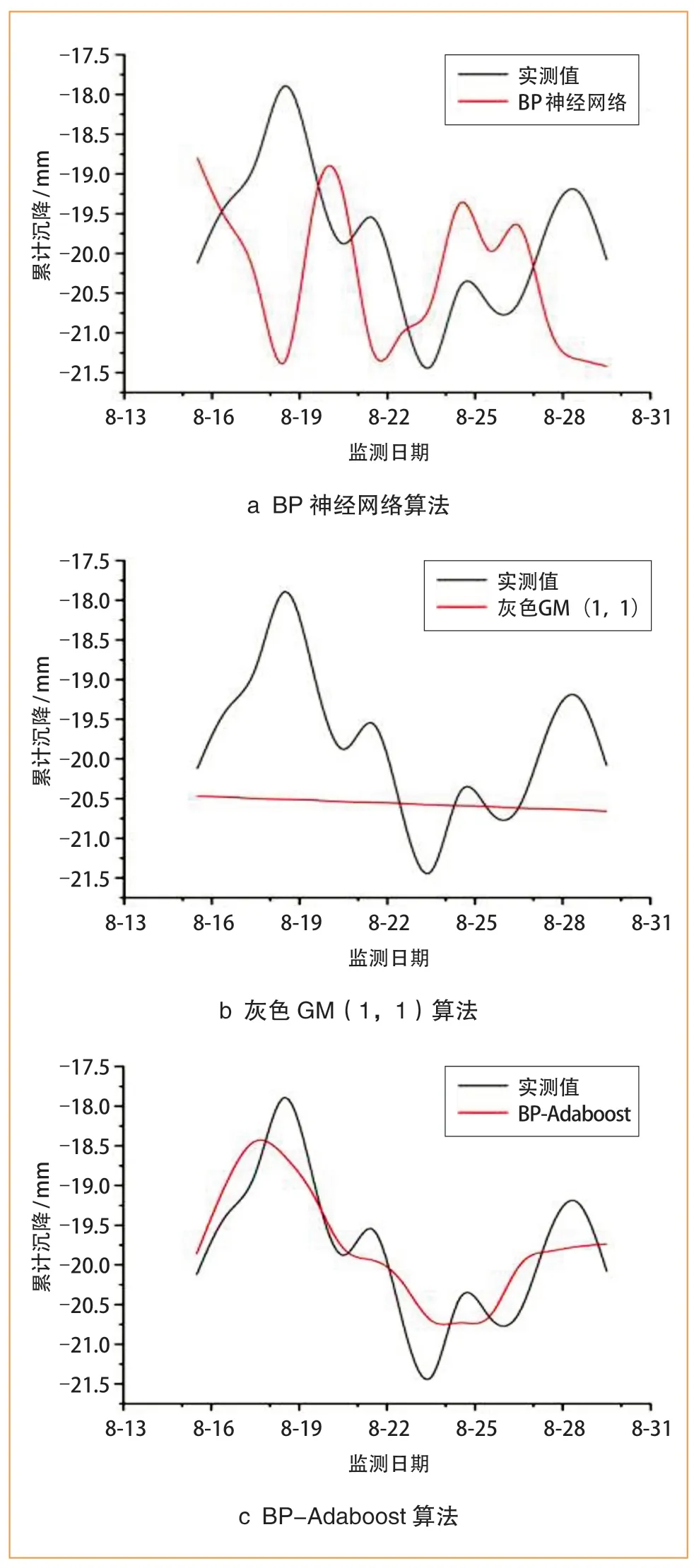
图3 3种算法预测数据与实测数据对比曲线