约束阻尼车轮振动声辐射特性及拉伸强度分析
向 琴,孙道永,徐 锋,胡晏晨
(中车青岛四方机车车辆股份有限公司,山东青岛 266111)
1 引言
高速列车具有快捷舒适、运量大、平稳安全、节能环保等特点,是当代多种尖端科技在交通领域中的充分运用,极大程度地便利了人们的生活。但随着高速列车速度的不断提高,随之而来的弊端也逐渐显现,轮轨相互作用不断增强,轮轨振动噪声问题越来越严重,使得乘客乘车体验度大幅降低。为降低轮轨之间振动产生的噪声,通常借助弹性车轮、谐振式降噪器和约束阻尼降噪板等方式[1]。其中,谐振式降噪器需对列车轮对进行机加工,会破坏车轮的结构强度;弹性车轮虽然降噪效果良好,但目前在高速铁路中运用很少;约束阻尼降噪板具有安装方便、高阻尼、维护成本较低等优点,在高速列车降噪方式中成为应用较为广泛的一种。
对于降噪方法的研究,国内外研究人员展开了深入的讨论与试验,其中包括列车车轮结构的优化设计、降噪材料及形状的优选以及合理选用粘接材料。S Cervello等人[2]研究不同约束阻尼材料和阻尼层厚度对车轮振动特性的影响,提出了损耗因子衡量指标,并在实验室和Firenze-Arezzo现场试验线分别进行了验证,结果表明在实验室和现场试验中车轮在添加阻尼层后噪声分别降低了约20 dB和10 dB。刘玉霞等人[3]从车轮添加阻尼方式和阻尼厚度2个方面,通过有限元模型进行仿真分析,验证了喷涂阻尼和约束阻尼2种不同阻尼施加方式在特定阻尼厚度下降噪效果可达到最佳。李牧皛[4]从振动特性和声辐射特性2个方面对喷涂阻尼车轮和约束阻尼车轮进行了研究,在自由悬挂和4 t轴重2种状态下分别通过力锤敲击试验和落球撞击试验测量降噪效果,实验结果表明2种阻尼车轮在不同状态下均获得了良好的降噪效果。Jones和Thompson[5]模拟具有不同刚度弹性元件的弹性车轮和不同约束层厚度的带约束层阻尼器车轮滚动下的噪声影响,与无阻尼车轮相比,其噪声分别降低2.5~4.7 dB和2.3~3.8 dB,且弹性元件刚度及约束层厚度的增加有助于车轮滚动噪声的降低。
以上研究主要是从仿真和试验2方面对不同阻尼形式下的降噪效果进行了研究,并没有对阻尼材料的粘接特性及可靠性进行分析研究。为探究安装约束阻尼板后车轮滚动噪声的降噪效果和阻尼层粘接强度,本文以某型高速动车组约束阻尼车轮为对象进行振动分析,通过Hypermesh有限元分析软件建立车轮与阻尼板粘接的有限元模型,研究动车在直线工况下施加约束阻尼的车轮振动特性及阻尼板粘接可靠性。借助Ansys有限元分析软件计算约束阻尼车轮的模态、谐响应分析和阻尼板极限粘接强度。
2 理论背景
2.1 模态分析理论
模态是结构的固有振动属性,每个模态都有其特定属性,包括固有频率、模态振型和阻尼比等。而模态一般通过模态分析手段获取,以便进行后续结构的振动特性分析。模态分析是近代研究结构系统动力特性的一种方法,归根结底,模态分析主要包括结构动力学中结构振动特征值和特征向量求解,而物理坐标系中的自由振动响应是由一种特定形态、自由振动的各阶主振动的线性叠加,振动频率又称系统的主频率,本质上是固有频率或阻尼固有频率。振动系统的运动微分方程表示形式如下[6]:
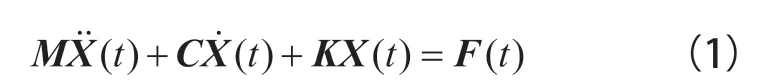
具有n自由度的无阻尼系统振动微分方程简化形式:
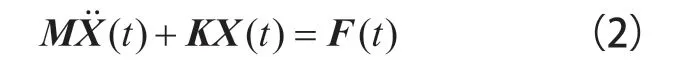
设特解为:

式(3)中,A为响应幅值矩阵。将式(3)带入式(2)中,系统自由振动频率方程式为:
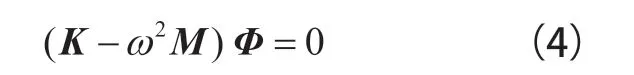
2.2 谐响应分析理论
谐响应分析,又称之为频率响应分析或扫频分析,作为确定结构受到简谐正弦激励时的稳态响应技术,适用于分析结构稳态受迫振动的情况。谐响应分析主要用于计算在某一激励频率下结构的响应特性曲线,并找到“峰值”响应。若系统在某激励频率下发生共振时,其位移会相对较大。通常采用3种方法计算谐响应分析,即模态叠加法、完全法和缩减法。
对于一般的受迫振动,系统的运动微分方程表征如下[7]:
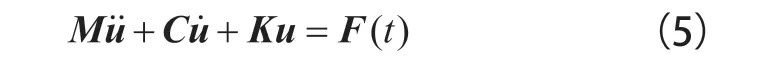
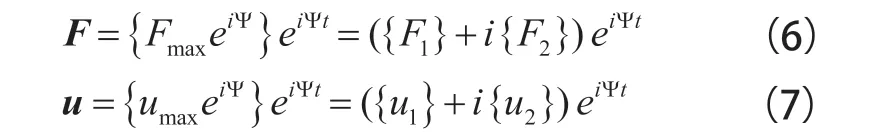
结合式(6)和式(7)并代入式(5)中,即可获得谐响应分析运动方程:
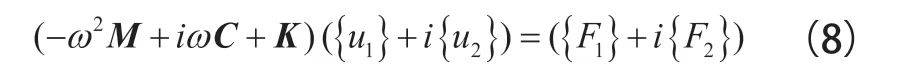
对于某一确定的线性系统对象来说,各阶模态振型的线性组合后即可获取响应即:
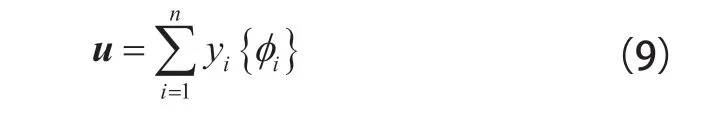
2.3 粘接分析理论
轨道交通行业已广泛应用粘接工艺,对于粘接过程的执行需严格遵守规范和要求。粘接定义为通过非金属材料以粘附和内聚2种方式来连接2种材料。粘接物破坏示意图如图1所示[8]。

图1 粘接物破坏示意图
如果被粘物与胶粘剂连接处即将发生破坏,被粘物与胶粘剂之间的粘附力将确定两者间的粘接强度。连接处粘接破坏实质上是弱界面层破坏。磨削加工时的剪切力、装配试验过程中的冲击等对于该粘接组件的粘接界面的破坏属于上述弱界面破坏形式。被粘物、胶粘剂、环境或它们共同作用的结果便是弱界面层的产生。弱界面层的产生过程,即当被粘物、胶粘剂及环境中的低分子物或杂质,通过渗析、吸附及聚集过程,在部分或全部界面内产生了低分子物富集区。粘接件在外力作用下的破坏过程发生于弱界面。这些因素导致粘接界面破坏且粘接强度严重下降。
为确保粘接强度,其承受最大应力值应在材料许用应力范围内,强度条件为[9]:
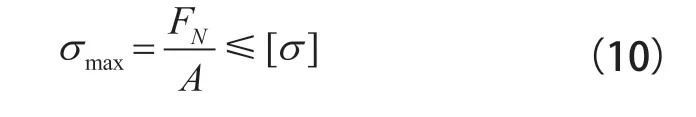
式(10)中,σmax为最大应力;FN为垂向力;A为受力面积;[σ]为材料许用应力。
阻尼材料的破坏变形主要是由畸变能密度引起的材料屈服,本文主要采用第四强度理论对阻尼层塑性粘接强度进行检验。对于引起材料破坏或失效方面,应力分析中主要采用von Mises屈服准则。其中,等效于复杂应力状态的单向相当应力计算方法为:
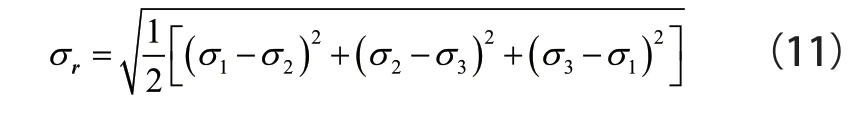
式(11)中,σ1、σ2、σ3为x、y、z3个方向主应力;σr为相当应力。
对于约束阻尼板粘接效果分析,是在安装约束阻尼板的车轮辐板上施加垂直于车轮的集中力,并对车轮最大应力值和最大位移进行分析,对其进行验证是否超出材料抗拉强度极限。
3 有限元建模及计算
本文研究对象约束阻尼车轮主要由高速列车车轮、阻尼层和覆盖在最外层的金属铝板3个模块组成。对其进行有限元分析前,首先应用SolidWorks软件对3个模块建模,然后按照规范要求将3个模块整合在一起,形成完整的三维模型。借助有限元分析软件Hypermesh对标准车轮和约束阻尼板车轮分别进行几何清理、网格单元划分,网格单元划分大小定为15 mm。有限元网格处理后的标准车轮和约束阻尼板车轮的有限元网格模型如图 2所示。无约束阻尼板的标准车轮与约束阻尼车轮分别划分为47 758个单元、52 427个节点和55 751个单元、61 245个节点,其中约束阻尼车轮中金属铝板划分为5 168个单元、5 443个节点。阻尼层共划分5 168个单元、10 883个节点。车轮和阻尼层采用Solid185单元,外部金属铝板采用Shell181单元进行有限元网格划分。
约束阻尼板车轮的材料及属性参考相关标准与文献如表1所示[10]。

图2 标准车轮和约束阻尼车轮有限元模型
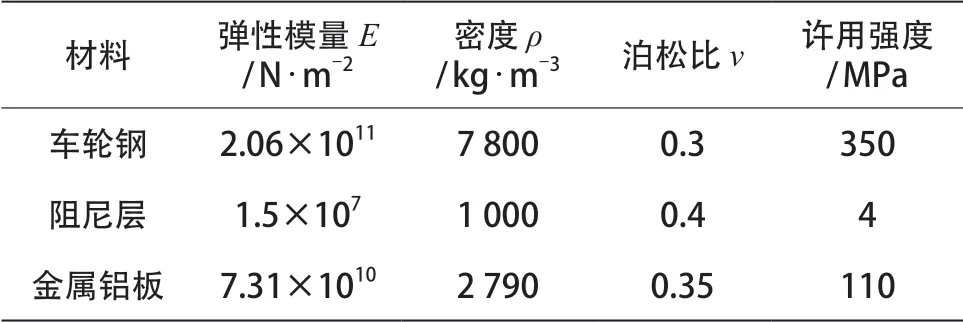
表1 约束阻尼板车轮材料及属性
4 结果分析与讨论
4.1 约束阻尼车轮模态分析结果
车轮的振动模态主要分为2类非平面振动,即节径振动和节圆振动[4]。节径振动定义为圆板过圆心的一条或多条直径位移保持为零的振动过程;节圆振动定义为圆板上一个或多个以上的与边界圆同心的圆的位移保持为零的振动过程。非平面振动可由(m,n)描述,其中,m,n分别为节圆数和节径数。节圆数为车轮振动幅值沿半径方向的分布特性;节径数为车轮振动幅值沿周长方向分布特性。而车轮受到的主要激励振动类型分别是0节圆轴向振动、1节圆轴向振动和径向振动。0 节圆轴向模态为踏面、轮辋轴向振动,1节圆轴向模态为辐板轴向振动,径向模态为轮辋径向振动,2节圆轴向模态为辐板振动。其中,1节圆和2节圆轴向模态及径向模态占轮轨振动噪声比例比较大。曲线啸叫噪声主要由0节圆轴向振动导致,所以通过抑制车轮的0节圆的轴向振动、径向振动以及两者间耦合振动可以在一定程度上降低车轮辐射噪声。对模型进行模态计算,模态频率如表2所示,部分模态振型图如图3所示。
根据表2,在车轮振动声辐射显著的频带范围内,标准车轮在安装约束阻尼板后,各阶模态所对应的固有频率变化不大。另外,径向模态频率升高,而0节圆和1节圆模态频率降低。轮轨噪声主要由轨道和轮缘间摩擦所致,所以约束阻尼板的安装可缓解轮轨间作用产生的高频共振带来的影响。
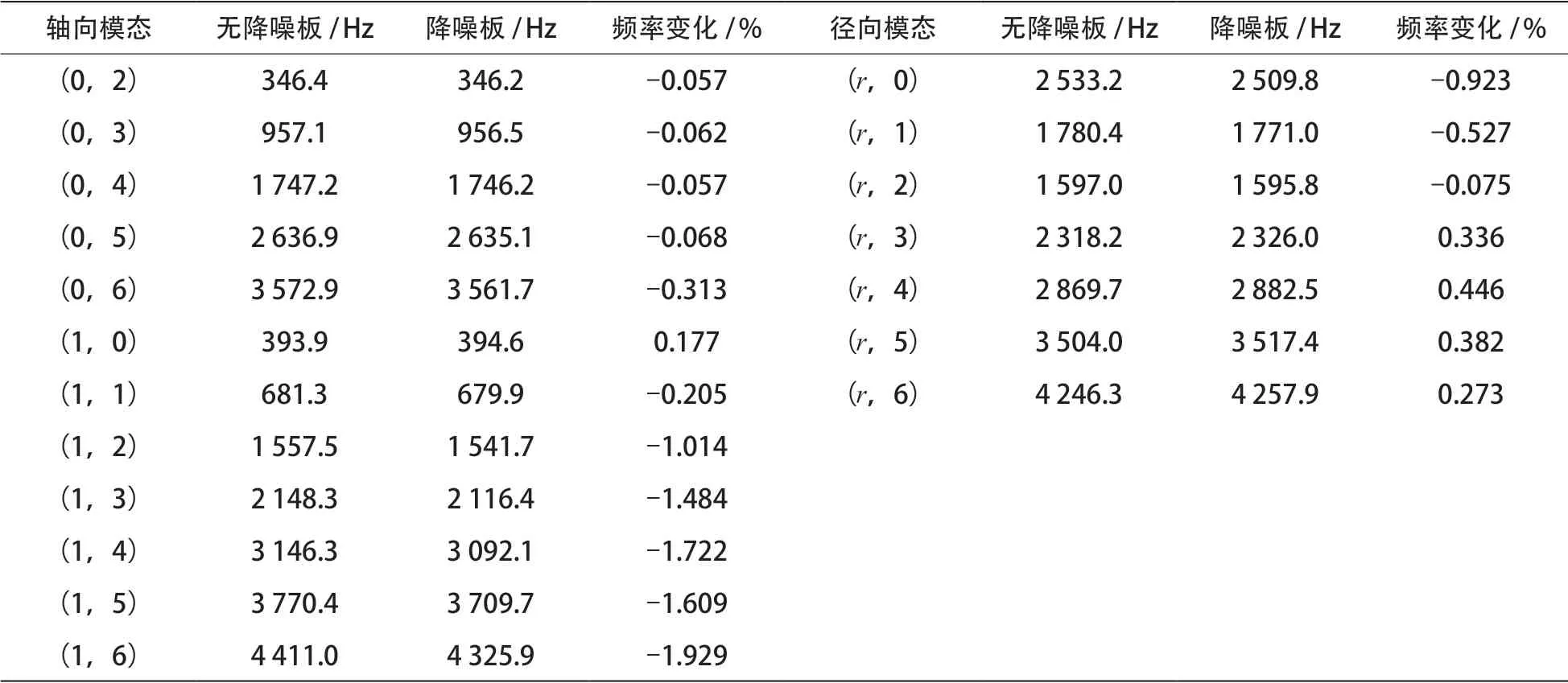
表2 高速列车车轮各阶模态
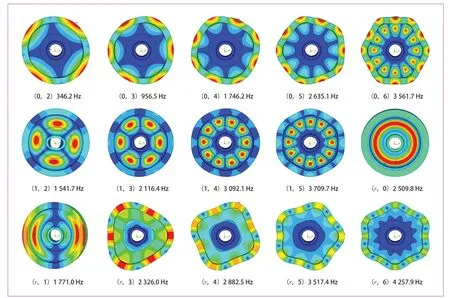
图3 约束阻尼车轮模态振型图
4.2 约束阻尼车轮谐响应分析结果
在谐响应分析中主要考虑约束阻尼车轮的直线运行工况,并假设位于名义滚动圆上的轮轨接触点为名义接触点。车轮谐响应分析加载示意图如图4所示。在7 787号节点施加激励,即车轮名义接触点处法向粗糙度的等效力激励。其中,水平方向上力F1选择幅值为1 000 N的正弦载荷,垂直方向上F2选择幅值为500 N的正弦载荷。另外,考虑到轮轨噪声主要分布情况[11],因此对约束阻尼车轮进行谐响应分析时,设置分析频率范围在50~4000 Hz。所加正弦载荷可表示为:F1= 1 000 sin(t+ 30°) ,F2= 500 sin(t+ 30°)。

图4 谐响应分析加载示意图
加载条件设定完成后,对标准车轮和约束阻尼车轮进行谐响应对比分析计算,得到加载点处UX、UY、UZ方向上的位移频率变化如图5所示。
从图5可以看出,标准车轮的共振峰集中在2 000~3 500 Hz,约束阻尼车轮的共振峰在UX方向上为2 700 Hz频率附近,在UY及UZ方向上为3 300 Hz附近。通过对比标准车轮和约束阻尼车轮在加载点处的变形可知,安装后的变形情况明显小于没安装的变形,说明约束阻尼板的安装可以有效降低振动传递函数幅值。此外,约束阻尼板在振动中能吸收振动能量,从一定程度上改变车轮的振动程度。可以看出,在车轮上添加约束阻尼板有利于轮轨振动时降低噪声和减少振动。
4.3 约束阻尼降噪板粘接强度分析结果
粘接强度仿真模拟实际拉伸试验中车轮辐板受力情况如图6所示。对约束阻尼板车轮车轴接触设置固定约束后,在车轮约束阻尼板施加垂直于辐板的拉力,选择200 N和350 N加载工况下的应力分布情况和变形进行分析。
(1)对约束阻尼车轮施加垂直于车轮约束阻尼板200 N拉伸载荷后,得到的von Mises应力和位移变形图如图7~图9所示。其中车轮钢层最大应力为3.48 MPa,最大应力位置为与阻尼层外圈边缘接触处;金属铝板层最大应力为43.36 MPa,位置为铝板内圈边缘;阻尼橡胶层最大应力2.46 MPa,位于阻尼层外圈边缘。最大应力都小于材料许用强度,不会发生粘接失效。
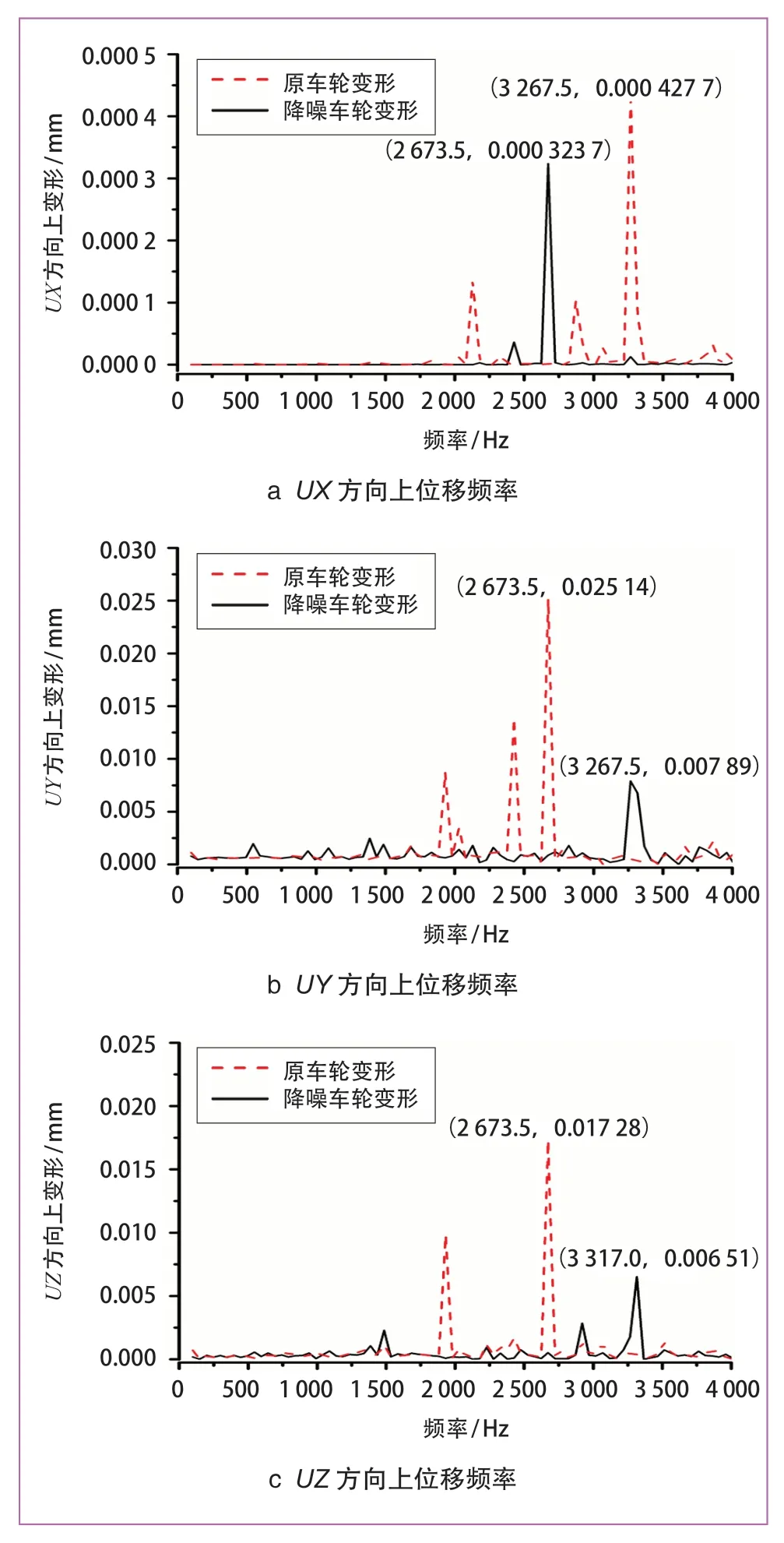
图5 标准车轮与约束阻尼车轮加载点处的位移频率图
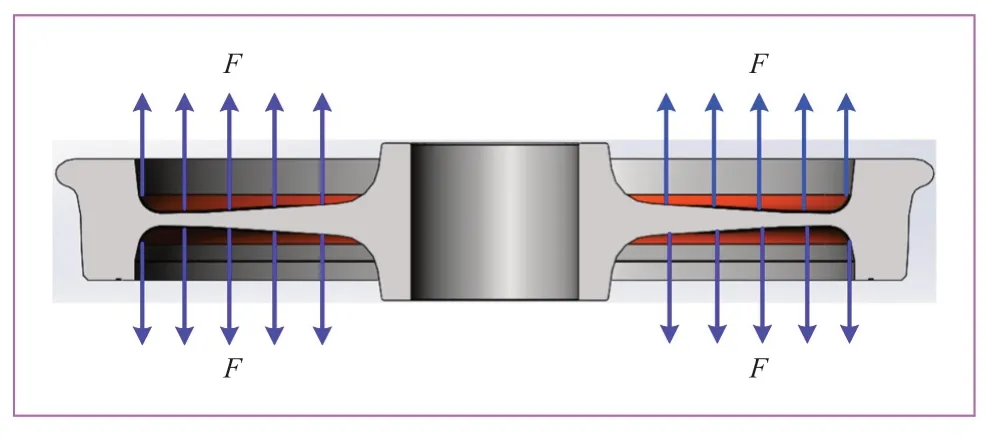
图6 拉力加载示意图
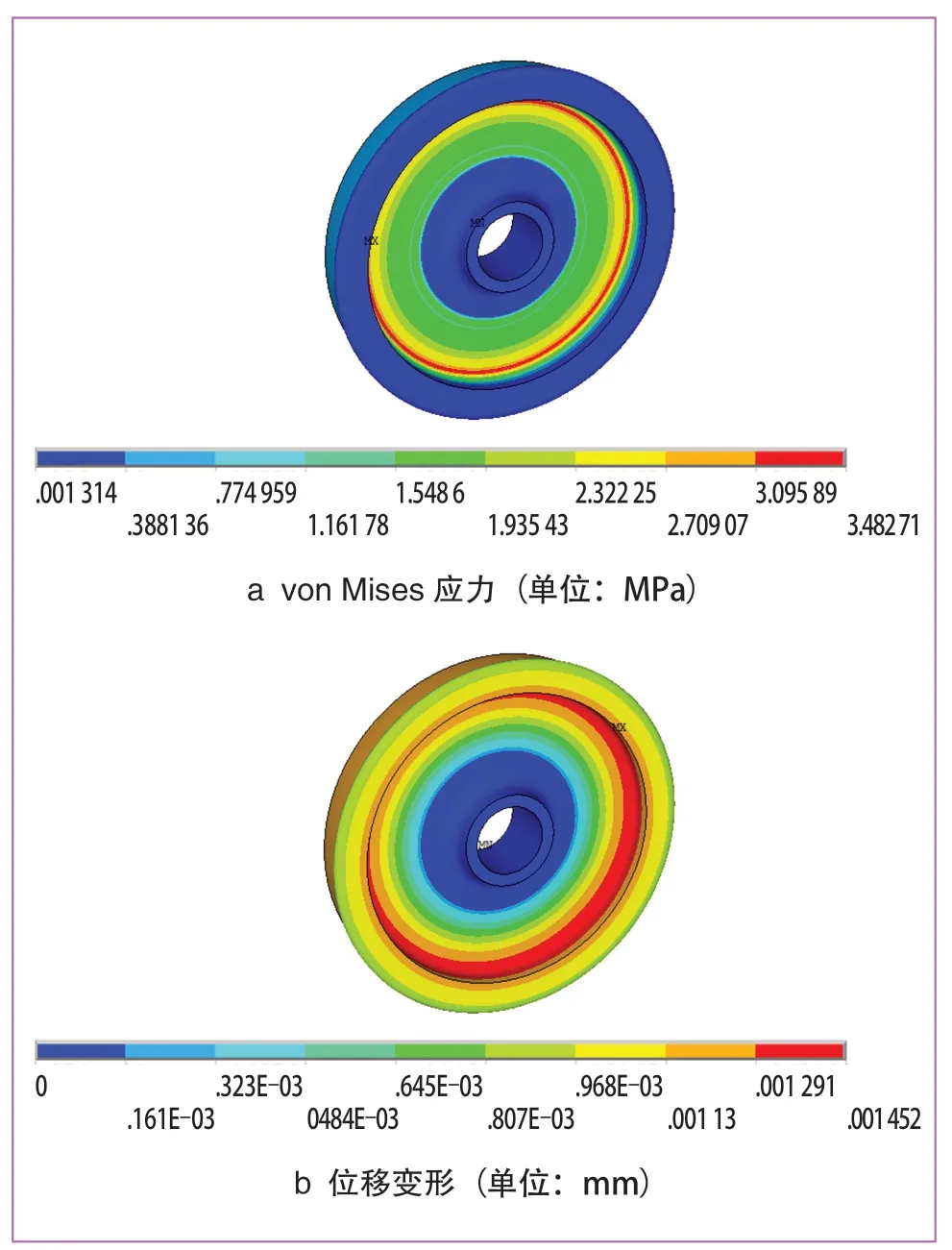
图7 200 N载荷下车轮应力及变形图
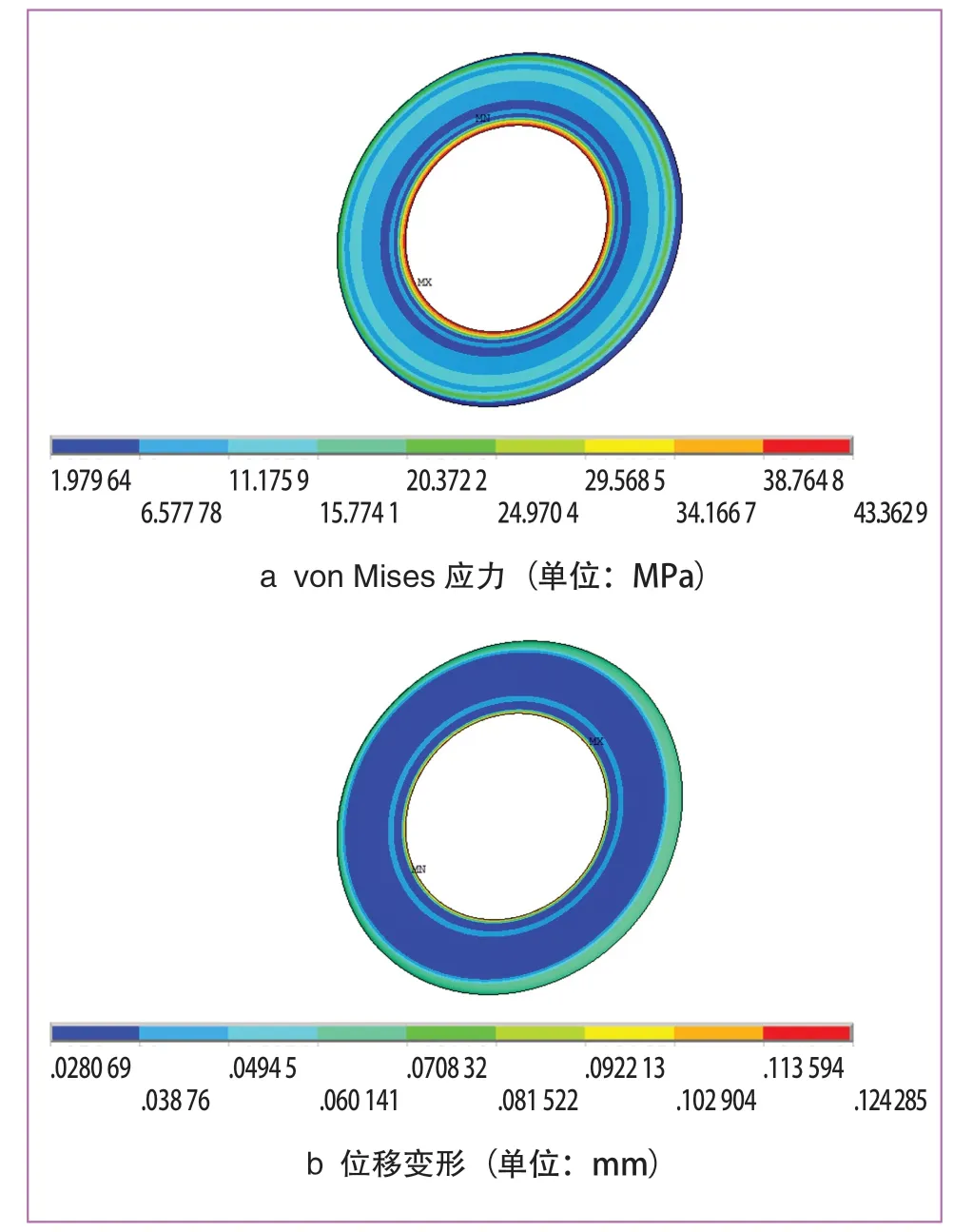
图8 200 N载荷下金属铝板应力及变形图
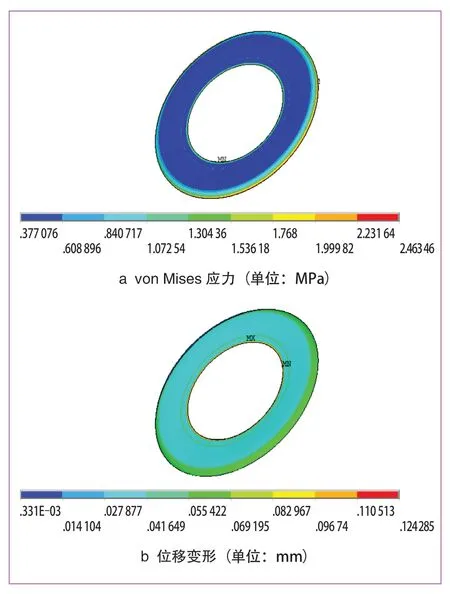
图9 200 N载荷下橡胶阻尼应力及变形图
(2)施加350 N拉伸载荷后,得到von Mises应力和位移变形图如图10~图12所示。车轮钢层最大应力为6.09 MPa,最大应力位置为与阻尼层外圈边缘接触处;金属铝板层最大应力为75.89 MPa,位置为铝板内圈边缘;阻尼橡胶层最大应力4.18 MPa,位于阻尼层外圈边缘。其中车轮钢层和金属铝板层最大应力小于材料许用强度,而阻尼橡胶层大于许用强度,发生粘接失效。各工况下粘接强度如表3所示。据上述各工况下约束阻尼板粘接强度仿真分析结果可知,在拉伸载荷小于325 N情况下,各工况下的粘接强度小于材料许用强度,约束阻尼板不会发生破坏现象。当大于325 N时,应力水平将超过阻尼橡胶层许用强度,约束阻尼板性能可能遭到破坏。
5 结论
本文以某型高速列车约束阻尼车轮为研究对象,分别在建立有无约束阻尼板的车轮有限元模型上进行模态、谐响应和粘接强度分析校核,结果如下。

图10 350 N载荷下车轮应力及变形图
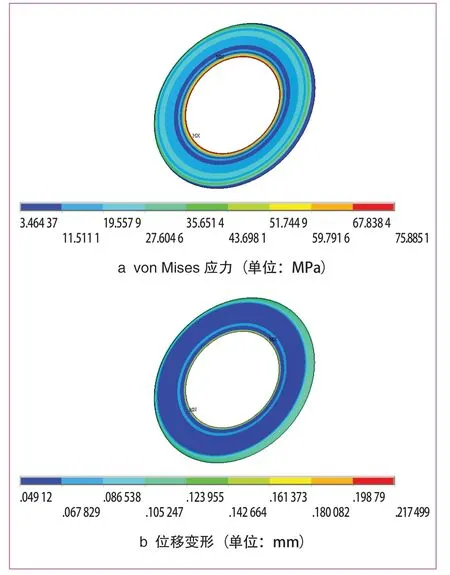
图11 350 N载荷下金属铝板应力及变形图
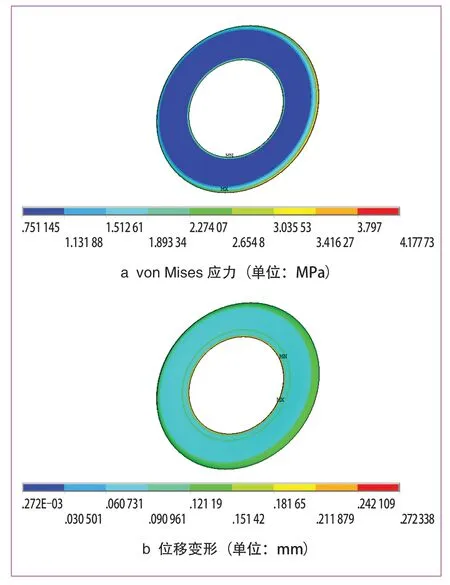
图12 350 N载荷下橡胶阻尼应力及变形图
(1)模态分析表明,标准车轮在安装约束阻尼板后,车轮固有频率受约束阻尼板的影响不大。其中,0 节圆和1节圆模态频率降低,说明安装约束阻尼板能有效削弱轮轨高频共振的可能性,有效避免高频共振带来的严重后果。
(2)谐响应分析表明,有约束阻尼板车轮在各主共振峰处的振动位移变形小于没有安装约束阻尼板的标准车轮在各主共振峰处的振动位移变形。说明约束阻尼板对于削弱轮轨振动影响的作用主要是通过其振动消耗更多的振动能量,以缓解轮轨间剧烈振动,从而有效改善车轮的振动传递特性。
(3)粘接强度分析表明,粘接约束阻尼板后的标准车轮具有一定抗拉伸性。在小于325 N垂向拉伸下不会发生粘接失效,大于325 N垂向拉伸下可能会发生粘接失效,粘接失效通常发生在约束阻尼层外圈边缘,在安装约束阻尼板工作时应注重阻尼层外缘粘接的可靠性。
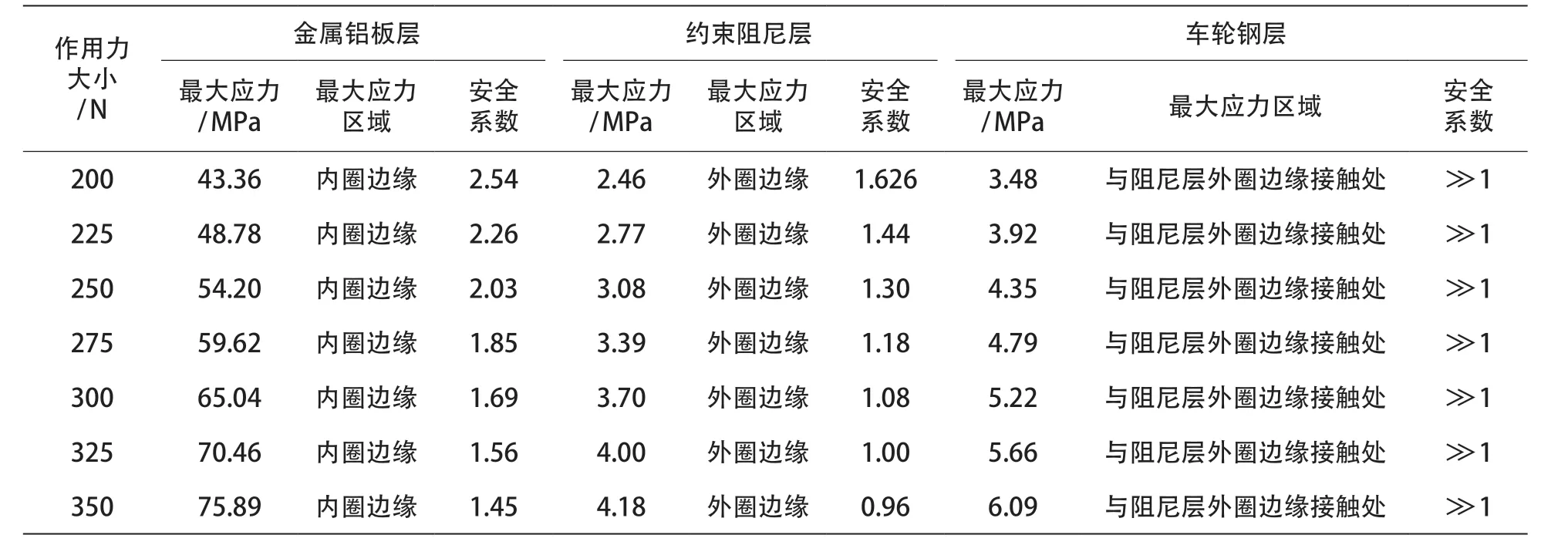
表3 不同工况下约束阻尼车轮粘接强度

