基于机器视觉的微型电子接插件尺寸测量
俞 洋,金 彬
(江苏理工学院电气信息工程学院,江苏常州 213001)
0 引言
传统的接插件尺寸测量方法,主要测量对象为普通尺寸或中大型工件,公差允许范围较大。目前接插件正在向小型化、微型化方向发展,传统测量方法在对微型电子接插件进行检测时,测量的核心环节还需要人工,一定程度上降低了检测效率[1]。由于微型电子接插件具有尺寸小、质量轻等特点,少量的微尘或图像阴影就可能造成数个像素点的偏差,从而导致测量结果不准确[2]。传统方法提高测量精度主要依靠环境无尘化以及镜头、照明设备的更新升级,代价较高。
本文提出一种新的微型电子接插件尺寸测量方法,提高了检测精度,保证产品的质量。本方法通过改进算法,解决了部分因微尘或光线阴影造成的边缘判定不准确导致的测量结果偏差大的问题,从而提高了尺寸测量的准确度。
1 微型电子接插件尺寸测量方法
本文提出的微型电子接插件尺寸测量方法,将相机采集到的图片进行处理,获取待测工件的边缘,并测算待测距离,将测量结果保存到JSON 文本中。微型电子接插件尺寸测量流程图如图1 所示。首先获取相机采集到的图像,并进行模板匹配,获取待测区域;其次,对待测区域进行图像滤波;接着,对滤波后的待测区域进行边缘检测,获取微型电子接插件的边缘;然后对获取的边缘进行最小二乘法拟合;利用相机的校准与标定结果,对图片进行校正,并测量最终尺寸。最后,将测量结果保存为JSON格式。
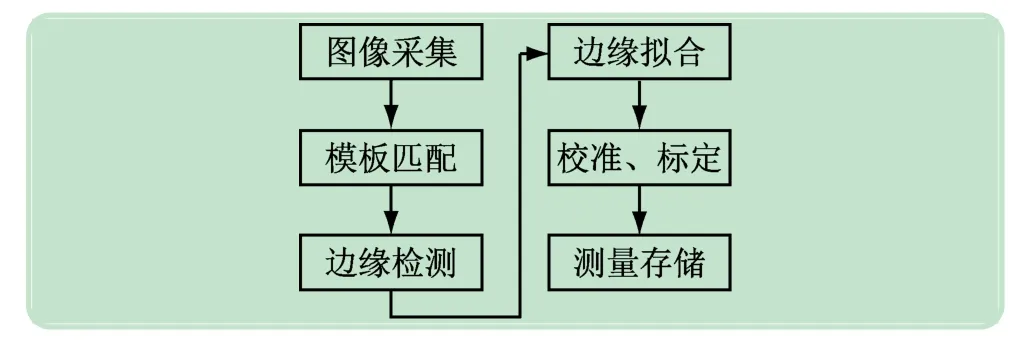
图1 微型电子接插件尺寸测量流程图
1.1 模板匹配
模板匹配也称为像素的模板匹配方法,是一种比较新型的图像轮廓的检测和识别方法[3]。在获取相机拍摄的图片后,通过模板匹配算法,将待测量区域找出,缩小图像处理的区域,从而提高后续图像处理流程的速度。
传统模板匹配算法需要各种角度旋转模板以达到匹配,速度较慢[4]。考虑到微型电子接插件在各生产流程中自带的料带孔、定位孔的特点,本文提出了一种基于图形的金字塔模板匹配算法,可以快速定位料带孔、定位孔以及其他定位图形的位置,进而定位待测件的位置,提高了模板匹配的速度。
新的模板匹配具体步骤如下:首先,算法采用2 ×2 均值滤波方法生成4 层图像金字塔;再使用3 ×3Prewit算子计算各层金字塔图像所对应的向量图;在顶层图像中进行基于形状的模板匹配,将最高层金字塔匹配所得信息带入低层金字塔跟踪匹配,并作必要的筛选,最后在底层金字塔图像进行基于形状的模板匹配,获取辅助定位图形的可能位置。
定位到辅助定位图形候选位置后,对候选位置进行筛选,以冲压料带为例,筛选原则为同一直线上的相同大小候选孔为真实定位孔。再以真实定位孔为定位基准,精确定位到待测区域,并进行待测区提取。
1.2 边缘检测
图像边缘检测是图像分析与检测的前提,其原理是提取目标与背景之间的边界信息[5],准确提取出图像边缘。在众多传统边缘检测算子中,Canny 算法的检测结果包含了图像更多边缘信息,能够取得更好的检测效果[6]。但传统Canny算法边缘检测极易受到噪声及光照变化等因素的影响,需采用高斯滤波器平滑图像,而如此一来会导致图像过于平滑,继而引发边缘模糊与细节丢失。目前已经有许多研究者为此做出了改进,比如:自适应高斯滤波器、形态学滤波、自适应阈值、自适应中值滤波等等[7-9]。本文在自适应阈值Canny算法上进行了改进。
改进的Canny 算法流程如图2 所示,首先对图像进行滤波,在尽可能保持边缘特性的前提下滤除噪声,从而获取较为理想的待测图片。然后对图像进行梯度幅值与梯度方向计算,获得待测区域的梯度图。再对像素点进行非极大值抑制,获取边缘点。随后采用改进的自适应阈值算法,计算全局阈值比例,再根据全局阈值计算局部高低阈值矩阵[10]。通过局部高、低阈值矩阵进行强、弱边缘划分,减小了边缘提取的误判率。对强边缘保留、弱边缘删除,对中庸点进行中庸边缘编号,将与强边缘相连但自身不闭合的中庸边缘进行删除,从而过滤掉部分微尘、毛刺的影响,进一步提高了边缘提取的准确性。
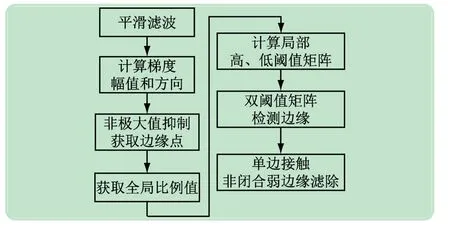
图2 改进Canny算法流程
1.2.1 滤波去噪
本方法中,放弃了传统高斯滤波器的平滑滤波方式,采用小波变换和中值滤波相结合的方式进行图像滤波。首先使用中值滤波方法滤除椒盐噪声,再对去噪后的图像进行小波分解,分解后的系数向量经过阈值化后再进行小波重构[11]。
1.2.2 计算梯度幅值和方向
本文采用Sobel 算子进行梯度幅值与方向的计算。传统的Sobel 算子有X(横向),Y(纵向)两个方向[12],公式如下:
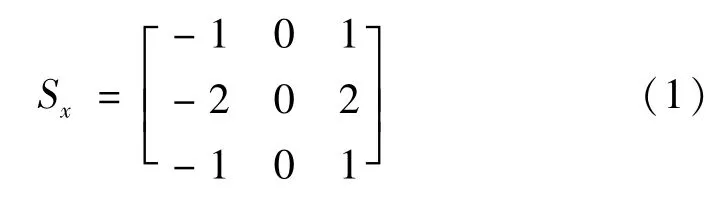
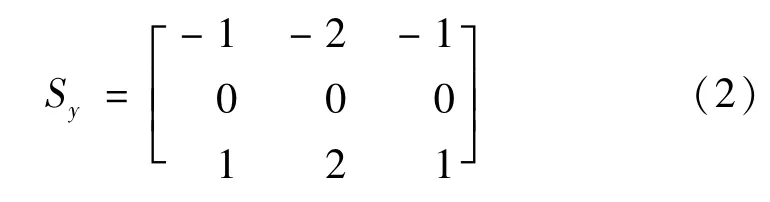
像素沿X方向的梯度为

沿Y方向的梯度为

式中:*为卷积符号;Arr为以该像素点为中心的3 ×3像素矩阵。
梯度幅值A(x,y)和梯度方向θ(x,y),
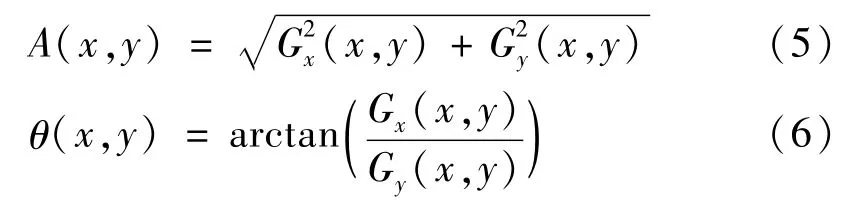
1.2.3 非极大值抑制获取边缘点
在3 ×3 像素邻域内通过插值获得梯度方向上的两个像素点值[13],并对梯度方向上的3 个像素点进行梯度幅值比较。如果当前像素点的梯度幅值比梯度方向上其他两个像素点的梯度幅值都要大,称该像素点为边缘候选点,标记为1;否则,标记为0。边缘候选点图像用A1(x,y)表示。
1.2.4 获取全局比例值
首先,利用大津法计算梯度幅值图A(x,y)的分割阈值,求得的阈值记为:T_val;再通过遍历灰度值矩阵,比较像素点灰度值与阈值的大小,统计出超出阈值的像素点数。计算不低于分割阈值的像素点数与图像总像素点数之间的比例,计算结果记为T_r,
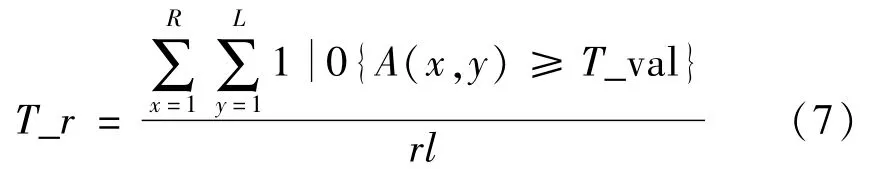
1.2.5 获取局部阈值矩阵
在梯度幅值矩阵A[r,l]中提取大小为s ×s 的局部矩阵块S,并计算当前局部块中心像素点的局部阈值T_s,要求局部阈值满足以下公式:
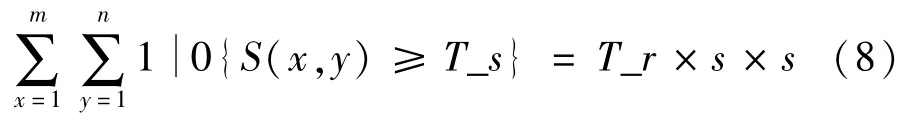
当前像素点的局部高、低阈值可以通过下式求得:
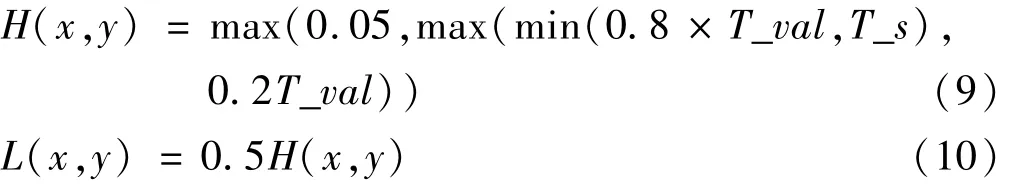
由于局部块S无法取到图像外,因此图片最边缘处,有数量为s/2 的像素点无法作为S的中心点,这些像素点称为“外圈边界点”,外圈边界点的局部阈值直接取邻近点的局部阈值。
1.2.6 边缘检测
采用如下步骤获取最终边缘:
步骤1获取边缘候选点的梯度幅值图
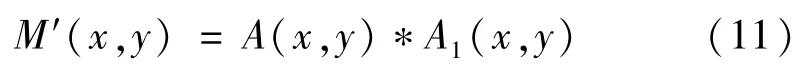
步骤2通过局部高、低阈值判定强、弱边缘点,并分别使用1 与0.5 标记强、弱边缘点
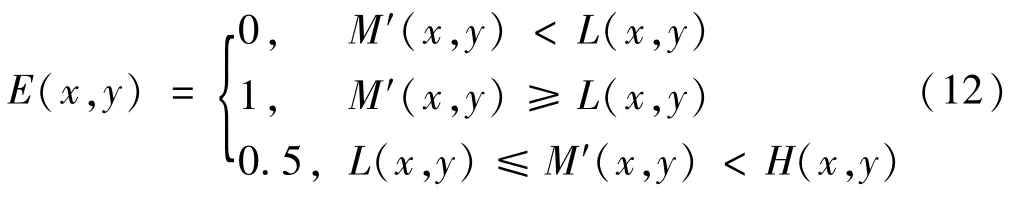
步骤3连接边缘,将强边缘点保留,与强边缘点相连且自身闭合的边缘保留,剩余边缘剔除:

从而得到最终边缘图像E(x,y)。
1.3 边缘拟合
传统的测量方法都是随机选取数个像素点,计算横、纵坐标平均值,根据计算结果进行距离测算。由于选取点的随机性,导致计算结果波动性较大。本方法中,对边缘进行最小二乘法拟合,将边缘信息函数化,测量结果稳定且更精确。
对已获得的梯度图中的边缘编号,分析局部范围内,同一编号边缘的梯度方向,判断当前边缘是否为规则边缘,如果是规则边缘,则进行拟合;如果不是规则边缘,则使用传统方法进行测量。
计算中,规则边缘尤其是直线的拟合,对多项式的次数要求较低;而当边缘为曲线时,拟合的多项式次数越高,拟合结果越精确,但随之带来的是计算量的增加[14]。因此,在非规则边缘区域,直接采用“数像素点”这样的传统方法,虽然精度无法提升,但是能够保持较快的测算速度。
1.4 相机校准和标定
1.4.1 相机的标定
为了实现通过像素计算实际距离,需要对相机进行标定,构建成像模型,建立图像像素点与微型电子接插件表面点位置的对应关系[15]。
假设相机与标定面(待测面)垂直,则有设计安装如图3(a)所示。此时,相机的模型为理想的小孔成像模型,物与像之间可以看作相似三角,其模型如图4 所示。理想模型中的换算比例K 为实际距离dr 与对应像素数dp的比值:

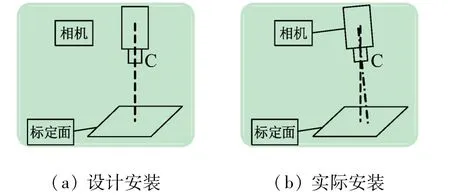
图3 设计相机安装示意图
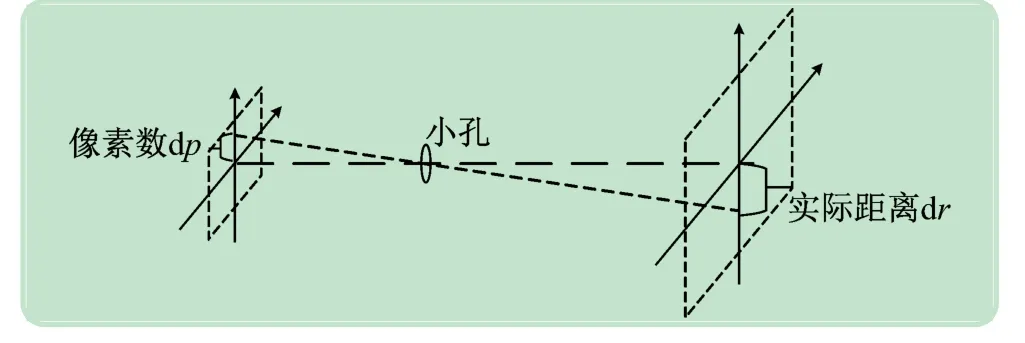
图4 小孔成像模型示意图
1.4.2 相机的校准
实际中,并不能保证相机轴线与待测面完全垂直,如图3(b)所示。相机光轴与标定面的垂线之间存在一个夹角。对于微型电子接插件来讲,很小的偏差角就可能使检测的边缘多出或者缩短数个像素点,从而使测量误差增大。
理想拍摄图像是相机轴线与拍摄面完全垂直,理想拍摄图片如图5(a)所示;实际情况下,由于非理想安装导致相机轴线与被拍摄面不完全垂直,从而引发另类的切向畸变,实际拍摄图片如图5(b)所示。
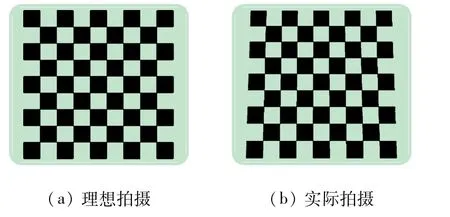
图5 标定图像拍摄效果图
可以将实际拍摄看作是理想拍摄的一个三维投影。为此,引入了一个透视变换模型,利用高精度的棋盘标定图片,提取棋盘角点信息与亚像素角点信息并通过标定公式进行参数标定,标定的参数可用于图像的畸变校正[16]:
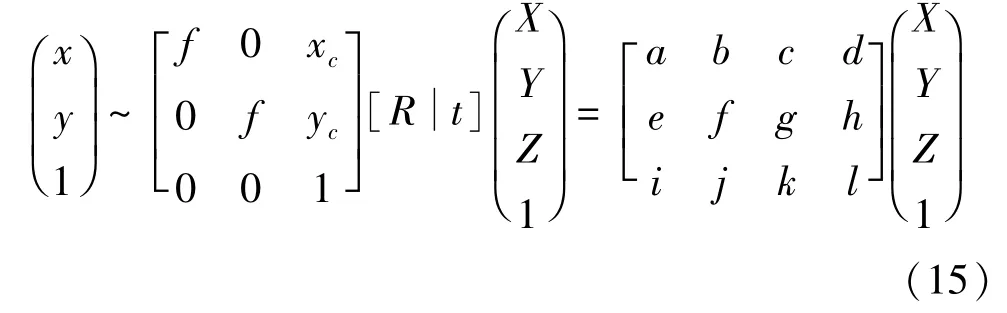
式中,相机内部参数的矩阵为
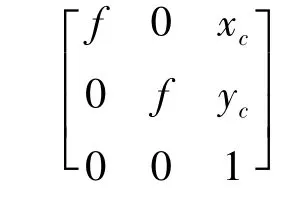
通过以上步骤获得的矩阵,在图像矫正过程中将畸变程度缩小,改善输入图像的质量,从而提高图像质量与测量准确度。
1.5 尺寸测量与存储
在得到相机的标定数据后,只需要测得图片中的像素点数就可得到对应的实际距离。常见的尺寸测量可归类为点到点、点到线、线到线的距离测量以及面积的测量。如图6(a)所示,计算点到点距离,直接使用勾股定理;如图6(b)所示,计算点到线距离,需构建点到线的垂线,再通过计算点到点距离来实现测距;如图6(c)所示,计算线到线距离,做出垂线与L1,L2相交,通过计算交点之间的距离来测量两平行线之间的距离。测量面积则通过统计所在区域的像素点数,计算像素点所对应的面积和。
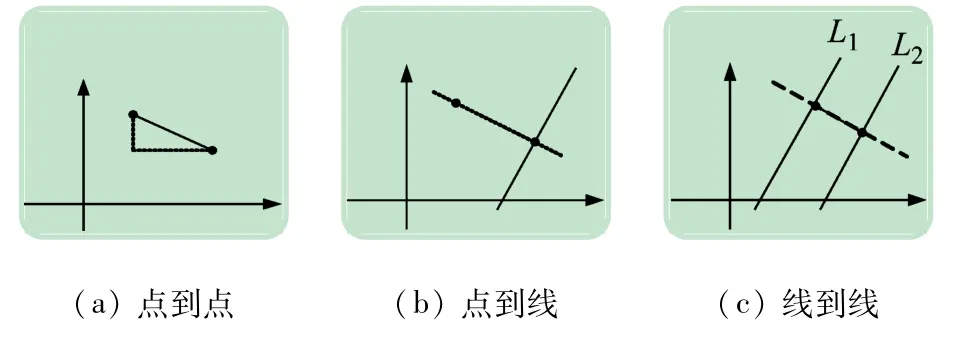
图6 3种测量方法示意图
在测得距离结果后,需要对结果进行保存,本方法分析比较了EXCEL、JSON、XML、数据库。综合分析,使用JSON格式来存储测量结果是比较好的方案。如果在速度要求不高的场合,也可以使用EXCEL表格方式进行存储,方便非专业人员进行手工分析。
2 微型电子接插件尺寸测量方法的实现与验证
本文以BK-3.0 微型电子接插件为例(见图7 实时图像区域),实现微型电子接插件尺寸测量方法并进行验证。
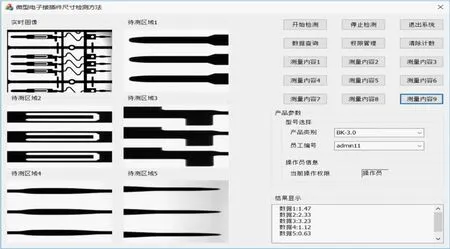
图7 软件界面图
验证方法的硬件系统主要由传动装置、PLC 控制器、工业相机、照明系统和工业主机(PC 系统)组成,测量系统结构如图8 所示。系统测量对象为BK-3.0微型电子接插件,高像素相机配合双远心镜头拍摄料带上的待测件,使用同轴光源与背光源配合提供光线。PC系统对工业相机将采集到的图片进行分析,并测量拍摄的工件尺寸,然后将尺寸以JSON 格式保存到外置硬盘,测量结束后PC系统向控制器发送信号,料带前进更新视野范围内工件。同时,根据当前拍摄到的图像是否为最佳视野范围,预测下一次的料带传动距离,该方案不需要光电传感器,避免了定位孔与物料中空部位重叠引起的定位错误问题。
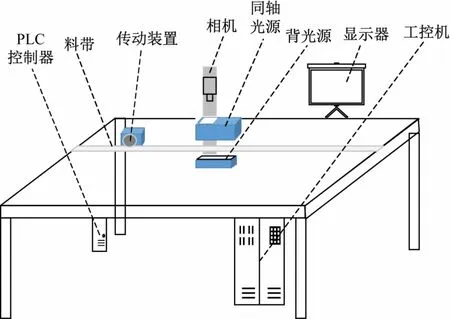
图8 微型电子接插件尺寸测量硬件系统结构图
2.1 微型电子接插件尺寸测量方法的实现
本文使用的视觉软件为Opencv 2.4.9,其具有众多图像处理算子和系统接口,可以方便地对图片进行各类存取操作;使用MFC 库进行人机交互界面的编写,界面如图7 所示。在图像窗口中,可以实时显示相机当前拍摄的图片、模板匹配后的待测量区域图片等;右上方的众多按键提供了丰富的查询、存储、导出等功能。右下角为文本窗口,可以显示测量结果,方便检测人员统计测量结果。
2.2 微型电子接插件尺寸测量方法的验证
本文选取了非接触式多元传感三维测量仪器(Optical Gaging products,OGP)测量仪测量后的20 个微型电子接插件为实验样本,以OGP 测量结果为标准,通过对比传统测量方法与本文测量方法的测量偏差值来验证本文尺寸测量方法的实际测量效果。对比试验中,传统检测方法与本文检测方法使用相同硬件设备条件,硬件架构如图8 所示。使用500 W像素相机,视野43 mm×35 mm,单像素尺寸约为0.017 mm,对每个接插件图片分别使用传统测量方法与本文测量方法进行指定区域对象的尺寸测量,并分别计算两种测量方法测得数值与OGP测量仪测得数值的偏差值。最终测量结果如表1 所示。
根据表1 中所展示的数据,绘制了两种方法测得的尺寸与OGP测量仪所测得的实际尺寸之间的偏差折线图,折线图如图9 所示,其中虚线为传统尺寸方法的偏差,实线为本文尺寸测量方法的偏差。
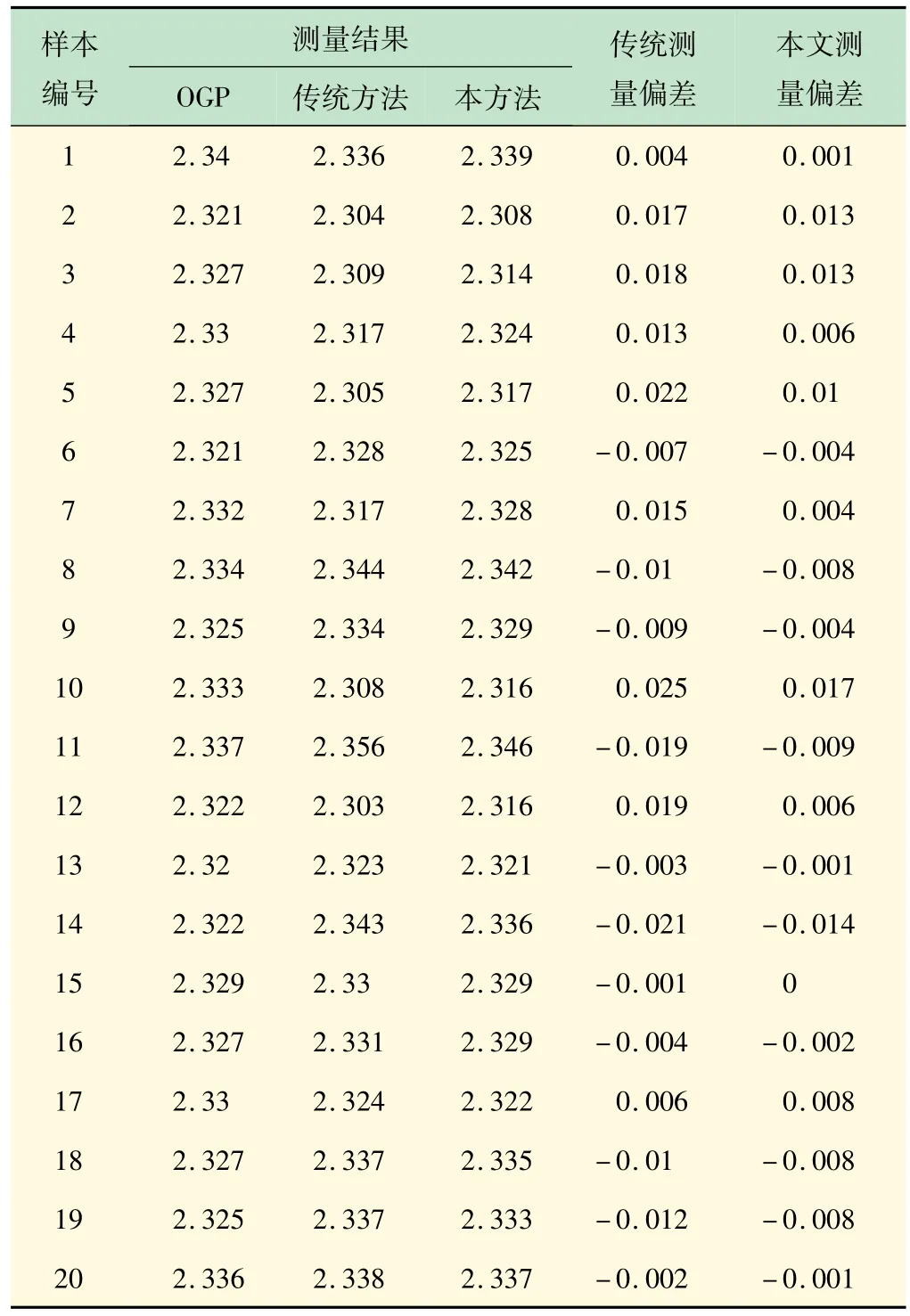
表1 微型电子接插件尺寸测量结果 mm
图9 显示了20 个样本分别使用传统方法与本文方法测得结果相对于实际值的偏差。从图中可以看出,本文提出的测量方法在测量准确度上有明显提高。其中,传统测量方法误差最大为0.025 mm,本文误差最大为0.017 mm,准确度提升了32%。
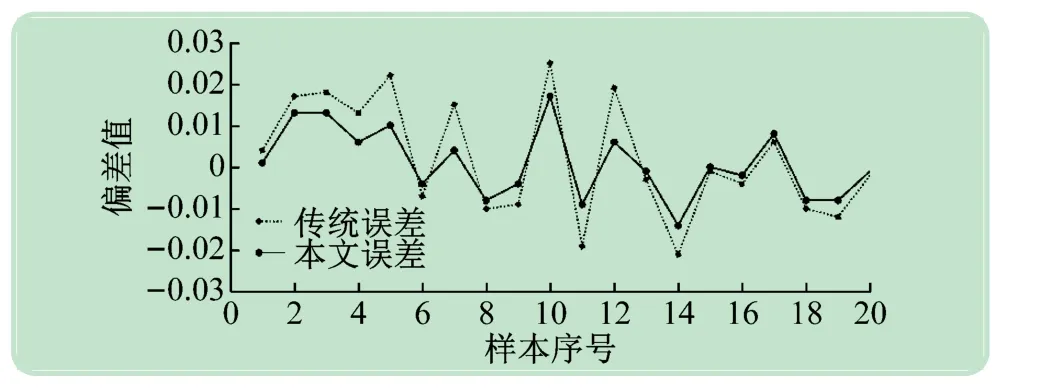
图9 偏差折线图
3 结语
本文针对传统检测方案存在微型电子接插件检测误差准确度不高的问题,提出一种新的微型电子接插件尺寸检测方法,该方法采用了快速定位的模板匹配算法、改进的自适应阈值Canny 算法、边缘拟合过程、相机标定与校准等一系列改进措施,减少了光线、微尘、非理想安装等因素对微型电子接插件的尺寸测量的影响。通过搭建实验软硬件平台,并以BK-3.0 微型电子接插件为被测对象进行验证,测量结果表明本方法的测量结果比传统检测方法测量结果在准确度上提高了32%,验证了本方法的有效性。

