遗传算法的涡旋光束畸变波前校正技术研究

梁 玮,周 峰,2,贺 君,曹智祥,元秀华,2

(1.湖南理工学院 信息科学与工程学院,湖南 岳阳 414006;2.华中科技大学 光学与电子信息学院,湖北 武汉,430074)

涡旋光束[1]具有轨道角动量(Orbital angular momentum,OAM),不同拓扑荷之间彼此正交,且理论上拓扑荷值可以无穷大,因而OAM是一种很有潜力的复用维度,成为大容量自由空间光通信的研究热点.2012年,Wang[2]等首次提出OAM模式复用机制,实现了4个OAM模式复用的 1.37 Tbit/s速率通信实验.Xie[3]等利用两束拓扑荷不同的拉盖尔高斯光束进行空分复用,实现了200 Gbit/s通信容量.Ren[4]等使用OAM复用与MIMO技术相结合实现16 Gbit/s毫米波通信.但是这些研究都没有考虑实际通信链路中大气湍流对OAM光束的影响,而严重时大气湍流能中断通信.为了降低大气湍流的影响,研究者提出了部分相干光传输[5]、大孔径接收技术[6]、波前校正[7]等一系列技术与方法.其中波前校正是最直接最有效的一种.

近年来,研究人员针对OAM光束波前校正展开了一系列研究与探索.Xie[8]等提出了一种基于Zernike多项式的随机并行梯度下降算法,实现了三个OAM模式复用的校正.Fu[9]等利用高斯光束探针的方法获取理想光场和畸变光场的光强分布，通过相位恢复算法求得OAM光束进行预补偿的校正相位.Li[10]等结合深度学习对OAM光束进行校正,结果表明该方法能使OAM模式纯度从0.19提高到0.61.但是,随机并行梯度下降算法容易陷入局部极值,GS算法对初始相位较为敏感,深度学习需要大量训练样本,因此需要寻求一种不易陷入局部极值、对初始相位不敏感、低运算复杂度的校正算法.遗传算法(Genetic Algorithm,GA)就具有不易陷入局部极值、初始相位不敏感的特性,因此,杨平[11]等利用遗传算法对畸变高斯光束进行校正,校正后的斯特列尔比值能够从0.032提高到0.96.然而利用遗传算法对畸变涡旋光束进行校正的研究未见报道.

本文基于无探针光束的自适应校正系统,结合Zernike多项式与传统遗传算法对涡旋光束进行畸变波前校正,并对交叉算子和变异算子进行对比研究,选取一组最佳的交叉变异算子对涡旋光束进行高质量的波前畸变校正.

1 理论基础

1.1 涡旋光束校正原理

涡旋光束的校正系统原理如图1所示.经过大气湍流后的畸变涡旋光束由成像相机采集光强分布图像,以光强相关系数作为遗传算法的适应度函数(即评价函数),通过算法搜索达到最优评价函数值时所对应的最佳校正相位,将其反馈给变形镜,完成闭环校正.

1.2 遗传算法

遗传算法是一种搜索算法,其原理是结合Darwin生物进化论学说,将寻优问题转化为类似物种之间的交叉、变异过程,保留较为优异的个体,淘汰差的个体,直至达到设定的优化目标值,其算法流程如图2所示.

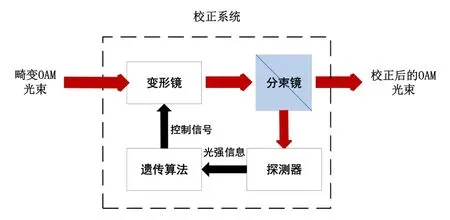
图1 OAM光束校正系统原理

图2 遗传算法流程

在常规基于遗传算法的自适应波前校正系统中,一般将变形镜驱动器电压作为算法种群个体,随驱动器个数增加,种群个体也将增加.这势必增加遗传算法的运算时间,进而延长波前校正时间.为了降低变形镜驱动器个数对波前校正实时性的影响,可将变形镜构建的校正相位用参数较少的Zernike多项式表示,即选择Zernike多项式的系数作为算法优化个体.其特点在于相对传统遗传算法而言,采用基于Zernike多项式的遗传算法提高了校正速度;相对于随机并行梯度下降算法,不易陷入局部极值.并且遗传算法中存在多种交叉变异算子组合,需要选取最优组合,本文通过选取最优的算子组合进行校正,进一步提高算法校正精度.

1.3 适应度函数

用遗传算法校正涡旋光束时,需要选择一个合适的性能指标,作为算法的适应度函数.但涡旋光束具有螺旋相位exp(ilφ),且中心存在相位奇点,光强分布成环状.常用的适应度函数,例如斯特列尔比、波前方差等已不再适用于校正OAM光束.由于OAM的远场光强分布与拓扑荷纯度正相关,因此光强相关系数可作为校正OAM光束的适应度函数,其定义为:

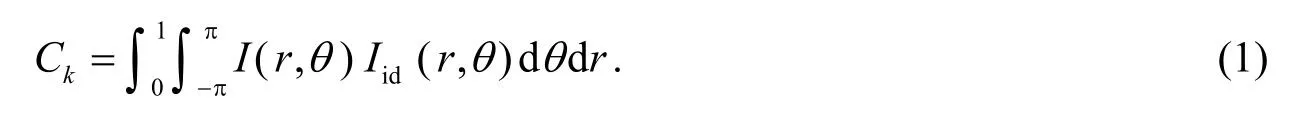
其中I(r,θ)为校正后的远场光强分布,Iid(r,θ)为理想的远场光强分布,相关系数越高,OAM光束的质量越好、模式纯度越高.

2 结果与分析

为了获得涡旋光束的最佳校正效果,首先分别对交叉算子和变异算子进行研究,对比在固定变异算子(或交叉算子)下,不同类型的交叉算子(或变异算子)的校正性能.然后选取最佳的交叉变异算子组合对畸变的涡旋光束进行校正,并验证其校正效果.最后对比了两点交叉和均匀变异、两点交叉和自适应变异、算数平均交叉和均匀变异三种组合下对单模和多模涡旋光束的校正性能.

2.1 交叉算子和变异的算子的选择

仿真实验的参量:束腰半径w0=3.5 ×1 0-3m,波长λ=1.55×10-6m,种群大小为100,选取前12阶Zernike多项式作为遗传算法的优化参数对象,采样点数为256×256,迭代次数为30次.

以畸变的单模涡旋光束(拓扑荷l=-1)为例,对比研究不同交叉算子、变异算子遗传算法的校正效果(图3).从图3(a)可以看出,两点交叉和随机二进制交叉算子具有更为优异的爬坡能力,而算数平均交叉和启发式交叉第一次爬坡能力较弱.从图3(b)可知,基于均匀变异、高斯变异、自适应变异算子的遗传算法校正后光强相关系数分别为0.62、0.71、0.79,说明自适应变异算子的校正效果优于其他两种.

图3 不同种类交叉算子(变异算子)的光强相关系数变化曲线

基于以上结果,选择两点交叉和自适应变异算子作为最佳算子组合,分别对畸变的单模和多模涡旋光束进行校正,并与算数平均交叉和均匀变异、两点交叉和均匀变异算子组合的校正效果进行对比.

2.2 单模涡旋光束校正

在不同畸变强度下,对单模涡旋光束(拓扑荷l=-1)进行校正,并对比三种交叉变异算子组合下的遗传算法的校正效果.仿真实验中采用Zernike多项式法产生相位屏,其畸变相位在-2～5 rad 范围内,认为畸变较弱,校正耗时、校正前后光强相关系数Ck和拓扑荷纯度见表1.

从表1可知,算数平均交叉和均匀变异、两点交叉和均匀变异、两点交叉和自适应变异组合算子校正后的光强相关系数分别能达到0.80、0.90、0.97,两点交叉和自适应变异算子组合的校正效果明显优于其他两种算子组合.

表1 弱畸变下单模涡旋校正结果

三种组合算子的遗传算法在较强相位畸变下(畸变相位范围为-4～10 rad)的校正前后光强相关系数、拓扑荷纯度的变化值和校正耗费时间见表2.两点交叉和自适应变异算子组合的遗传算法的光强相关系数能从0.19增加到0.79,拓扑荷纯度能从0.15增加到0.97,而算术平均交叉和均匀变异算子的遗传算法的光强相关系数只能增加到0.54,拓扑荷纯度只能上升到0.56,说明两点交叉和自适应变异算子组合在两方面都明显优异其他两种算子组合.

表2 较强畸变下单模涡旋校正结果

三种算子组合校正前后的远场光斑如图4所示.不难看出,校正后光强分布变得均匀,其环状光斑形状变得规整,尤其两点交叉和自适应变异组合的校正后的光斑与原始单模涡旋光束光斑最接近.这与上述光强相关系数的结论一致.

图4 单模涡旋光束校正前后远场光斑

2.3 多模涡旋光束校正

对畸变相位为-4～10 rad 的多模涡旋光束(拓扑荷l=1,-2)进行校正,对比算数平均交叉和均匀变异、两点交叉和均匀变异、两点交叉和自适应变异三种组合遗传算法的校正效果.

图5为固定选择算子为随机锦标赛算子,三种组合的遗传算法的光强相关系数的变化曲线.可以看出,两点交叉和自适应变异算子的遗传算法在该畸变情况下,光强相关系数能从0.16校正到0.78，而算术平均交叉和均匀变异算子只能校正到0.4.说明两点交叉和自适应变异算子的遗传算法对多模OAM光束的校正效果最好.

三种组合的遗传算法多模OAM光束校正结果见表3.可以看出,对多模涡旋光束而言,其拓扑荷l=1的拓扑荷纯度可以从0.4增加到0.6,拓扑荷l=-2的拓扑荷纯度可以从0.08增加到0.33,校正耗费时间差异不大.说明两点交叉和自适应变异算子组合对多模OAM光束的校正效果同样优于两点交叉和均匀变异算子、算术平均交叉和均匀变异算子组合.

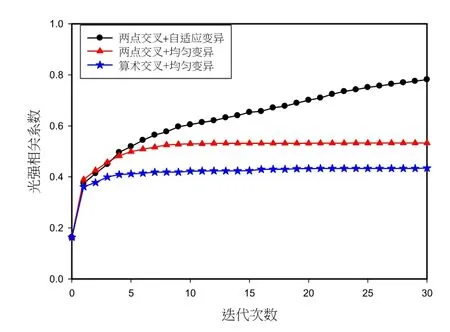
图5 基于三种组合算子的遗传算法Ck变化曲线

表3 较强畸变下多模OAM校正结果

三种算子组合校正前后的远场光斑对比如图6所示.从校正后的远场光斑可以看出,两点交叉和自适应变异算子校正后的光强增强,且光斑形状与原始多模涡旋光束一样呈清晰的花瓣状,而其他两种算子组合校正后的光斑不够规整.

图6 多模涡旋光束校正前后远场光斑

3 结论

本文针对无探针光束的自适应系统,采用结合Zernike多项式遗传算法对单模和多模涡旋光束进行校正研究,并对比了两点交叉、算术平均交叉和均匀变异、自适应变异的不同组合下的遗传算法的校正效果.实验结果表明,对单模涡旋光束而言,基于两点交叉和自适应变异的遗传算法的校正结果优于其他两种算法,在弱畸变下,校正后的光强相关系数能达到0.97;在较强畸变下,光强相关系数从0.19校正到0.79;拓扑荷纯度从0.15提升到0.97.对多模涡旋光束而言,在较强畸变下,基于两点交叉和自适应变异算子的遗传算法校正后光强相关系数从0.16增加到0.78.因此,采用两点交叉和自适应变异算子组合的遗传算法,有望促进高质量、大容量自由空间光通信系统的实现.