矩阵合同与矩阵相似的教学探讨

周潘岳

(湖南理工学院 数学学院,湖南 岳阳 414006)

矩阵合同与矩阵相似是高等代数中两个很重要的概念.在现有的教材和课堂教学中,很少把这两个概念放在一起来讨论.本文结合实际教学经验,从矩阵合同与矩阵相似的定义出发,进行类比讨论,并结合例子研究它们之间的关系.最后,将讲解过程录制成微课的形式,让学生更加清晰明了地掌握该知识点.

1 定义剖析

对矩阵合同与矩阵相似的定义分别进行阐述,并加以剖析,以便于比较两者的异同,深刻理解这两个概念.

矩阵合同设A,B是数域P上的n×n矩阵,如果存在数域P上的可逆n×n矩阵C,使得B=CTAC,则称矩阵A与B是合同的.

我们从定义出发来深刻理解这个概念.

(1) 定义中对矩阵C只要求存在,并没有要求唯一.

(2) 两个矩阵合同的前提条件是它们必须是同阶方阵.

(3) 在矩阵合同的定义中并没有要求矩阵是对称的,即两个不对称的矩阵也可能是合同的.

(4) 从定义中可以看出,如果两个矩阵是合同的且其中一个矩阵是对称的,那么另一个矩阵也一定是对称的.这个条件作为两个矩阵合同的必要条件往往用来证明两个矩阵不是合同的.

在实践教学中,学生总是很自然地认为合同矩阵一定是对称矩阵.这是因为合同矩阵的定义来源于二次型,任意二次型经过一个非退化的线性替换化为另一个二次型,这两个二次型对应的矩阵就是合同的,而恰巧这两个二次型对应的矩阵也是对称的.因此,学生总是错误地认为“若两个矩阵合同那么这两个矩阵一定都是对称矩阵”.事实上,这只是一个特例,矩阵合同的定义中并没有要求两个矩阵一定是对称矩阵.那么,在讲解矩阵合同的定义时教师应立即给出具体的例子以消除学生的误解.

矩阵相似设A,B是数域P上的n×n矩阵,如果存在数域P上的可逆n×n矩阵C,使得B=C-1AC,则称A与B是相似的.

我们也从定义出发,来深刻理解这个概念.

(1) 定义中矩阵C只要求存在,并没有要求唯一.

(2) 两个矩阵相似的前提条件是它们必须是同阶方阵.

(3) 从定义中可以看出,如果两个矩阵是相似的,则它们的行列式相等.但两个矩阵合同不一定满足这个条件.

2 矩阵合同与矩阵相似的关系

矩阵合同和矩阵相似的定义看似非常相似,仅在满足的条件上有差别.那么很自然会思考,它们之间是否有一定的关系或是能否互相推出呢？这是值得探讨和研究的问题.分析两个相似概念之间的关系也是更好地理解定义的一种常用的方法.

(1) 矩阵合同是否一定矩阵相似呢？

(2) 矩阵相似是否一定矩阵合同呢？

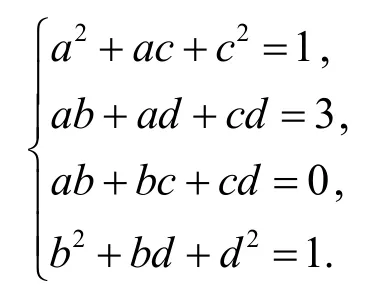
方程组中的第二个式子减去第三个式子,即得|C|=ad-bc=3,进而有 |C|2=9.由于CTAC=B,则有这与 |C|2=9矛盾.因此假设不成立,即A与B不是合同的.从这个例子可以看出,两个矩阵相似但不一定合同.

综上可知,矩阵合同与矩阵相似并没有必然的联系.

(3) 特殊矩阵之间的合同与相似

众所周知,任意一个方阵一定与本身既是合同的也是相似的.进一步我们探究满足什么条件的两个矩阵既是合同的又是相似的？

定理如果A,B是n阶实对称矩阵且它们有相同的特征值,则矩阵A与B既合同又相似.

证明不妨设A,B的特征值为λ1,λ2,…,λn,因为A,B均是实对称矩阵,则存在正交矩阵C1,C2,使得

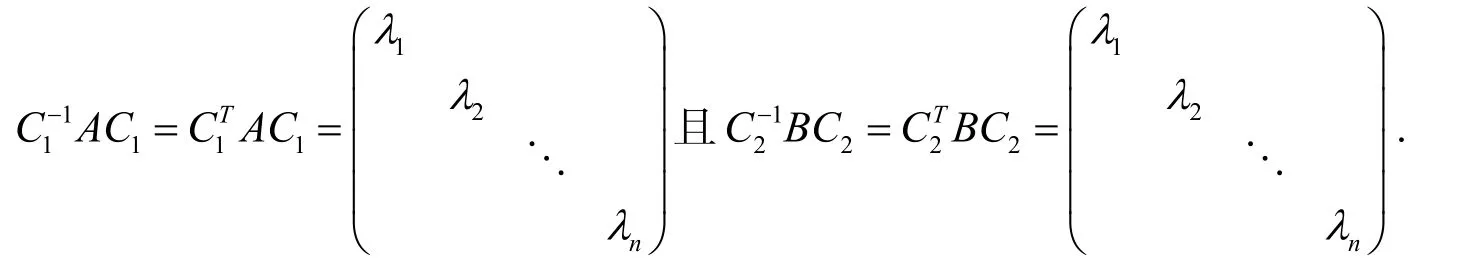
令C=C1,因为C2是正交的,那么也是正交的.因为、C1都是正交的,则C是正交的,从而有C-1AC=CTAC=B.因此A与B既合同又相似.

3 结论

高等代数课程是数学与应用数学专业的基础课程之一,也是考研的必考科目.而目前课程的现状是课时紧,任务重.在有限课时内将所有内容按部就班地讲完已不易,更不用说再讲解这些概念之间的联系与区别.但将知识点联系起来学习既可以加深印象又可以更好地理解,还能将零散的知识有机结合起来.针对现状,笔者建议将以上内容录制成微课视频,让学生利用课余的时间观看学习,作为课堂讲解的补充.如此既可以节约上课时间,又能留时间给学生自己思考,锻炼学生独立思考问题的能力,激发他们学习的主观能动性,达到双赢的效果.