基于灰色模糊物元预测的新乡市大气环境质量评价

王佳楠,程港桠,校园齐,李嘉伟,程启先

(1.山东师范大学 地理与环境学院,山东 济南 250358;2.信阳师范学院 地理科学学院,河南 信阳 464000;3.南京信息工程大学 环境科学与工程学院,江苏 南京 210044)

0 引言

大气环境是生态环境的重要内容,大气环境质量评价是大气环境质量规划与管理工作的必要基础[1].灰色系统理论在信息部分明确的研究中被广泛运用[2],一些学者将灰色系统理论的方法运用在大气与生态环境评价中,如灰色关联、灰色聚类、灰色预测等[3～5],但这类模型在样本量较多时不能保证其精度,限制了灰色系统理论的进一步拓展;部分学者尝试将人工神经网络[6,7]引入到大气与生态环境评价的研究中,试图弥补灰色系统理论的不足,但人工神经网络对样本数据量要求极高,即样本量对其精度有着直接影响,且易出现结果不直观、推理依据与过程不明确等问题.

灰色模糊物元分析是集灰色系统、模糊数学、物元分析等理论于一体的现状评价方法[8],并融入模糊隶属和可拓集合等概念,在不确定性或求解不相容等问题中尤为适用,现已应用于工程学、管理学等[9,10]领域;灰色模糊物元分析在适中样本量的研究中取得了较好效果,其结果直观、清晰、准确,但仍存在预测性评价较为薄弱的问题.本研究考虑将灰色预测模型与灰色模糊物元分析相结合,将其扩充为新的灰色模糊物元预测模型,能够弥补灰色预测模型在样本量增加时其精度下降的缺点,拓展灰色预测模型的应用范围.

本研究构建灰色模糊物元预测模型,通过对新乡市2015～2019年大气污染的面板数据进行大气环境质量评价,验证该方法在模糊环境下多指标优化问题中的可行性与有效性,以期为大气环境质量评价的相关研究提供一定的借鉴和参考.

1 研究区域与方法

1.1 研究区域

新乡市位于河南省北部、黄河海河流域交汇处,属于典型的暖温带大陆性季风气候,四季分明,夏季高温多雨、冬季寒冷干燥,年均降水量介于549.9～644.4 mm之间,年平均气温14℃,年均无霜期205天.新乡市是中原城市群的重要城市,经济总量位居河南省前列,是以电子、机械、化工等产业为主的工业城市,生态环境污染较为严重.近年来为开展大气污染治理工作,新乡市投入大量人力与物力,但治理效果并不显著,当前大气污染形势依旧严峻,大气污染治理工作任重而道远.

1.2 数据来源

本研究数据来源为新乡市生态环境局官方网站中的《新乡市空气质量月报(2015～2019年)》(https://xxhb.gov.cn/news/59),依据《环境空气质量标准(2012版)》[11]的要求,包括固态污染物和气态污染物2类,PM10、PM2.5、SO2、NO2、CO和O3这6个指标及其单位、权重等,具体情况见表1.

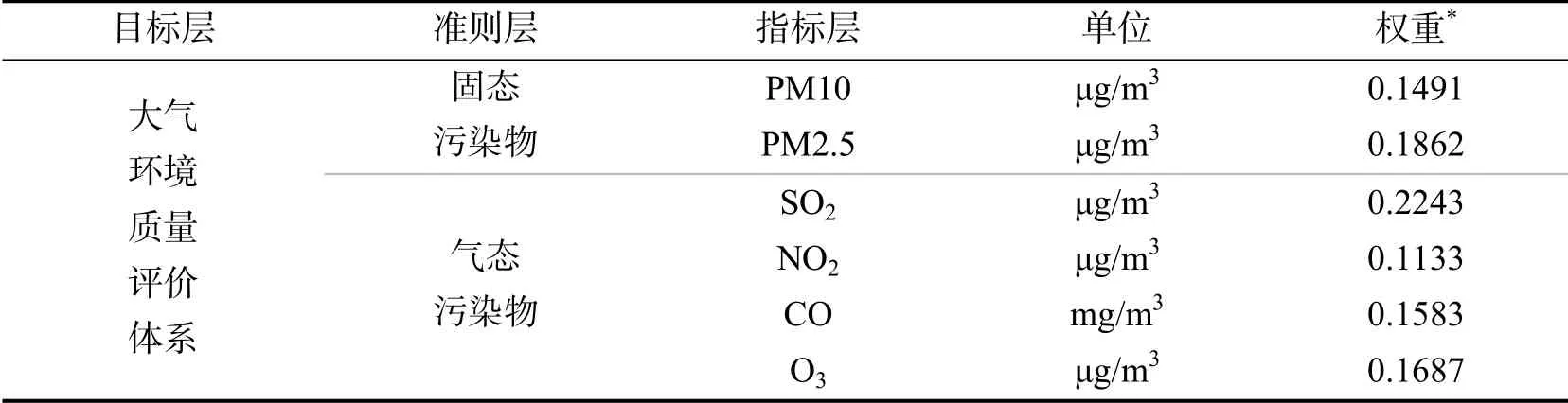
表1 评价指标体系

针对研究中存在的部分数据缺失情况,除CO外其余指标的缺失程度都较为轻微,缺失数据均采用SPSS 23.0中的“临近点的线性趋势”进行插值补全,并在补全后统计数据的最大值、平均值和标准差等数据特征,具体情况见表2.

1.3 研究方法

常见数据标准化处理方法有min-max法、Z-score法、归一化法和均值法等,常见的数据权重计算方法有Delphi法、AHP法、熵权法和均方差法等.考虑到运算的便捷性和准确性,本研究采用均值法和均方差法进行数据标准化处理和权重计算,公式如下[12,13]:

其中Xi′j是i时期j指标的原始数据,Xij是i时期j指标的处理数据,σj是j指标的均方差,是j指标的平均值,Wj是j指标的权重值.

本研究采用灰色模糊物元预测模型进行新乡市大气环境质量评价的实证研究.灰色模糊物元预测模型由灰色模糊物元分析和灰色预测模型两个部分组成,运用Matlab 2017对该模型进行运算和检验,部分公式如下[14,15]:

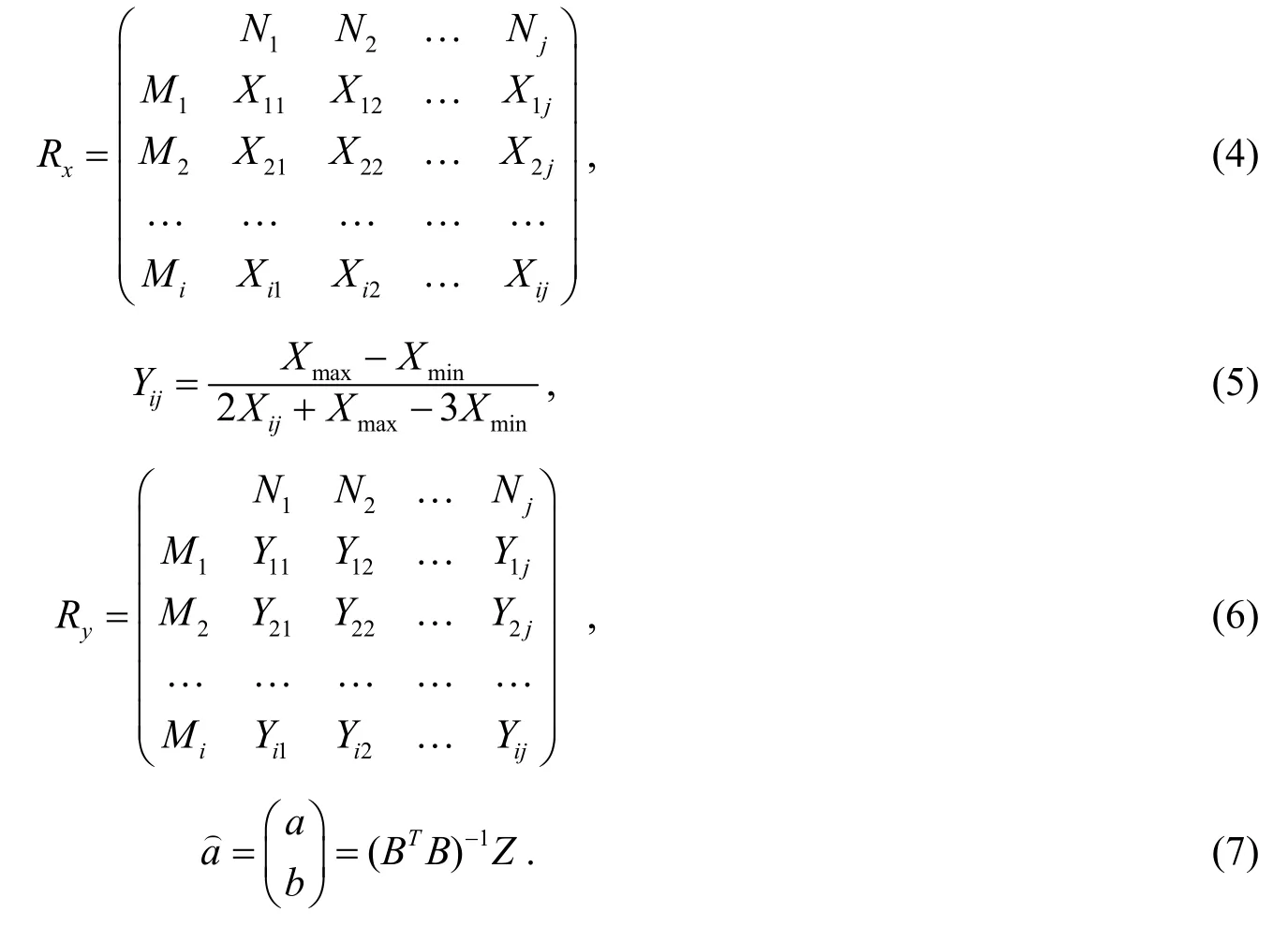
其中Mi和Nj分别为i和j的构成列,Xij和Yij分别为初始和结果的数值,Rx和Ry分别为初始和结果的矩阵,灰色预测模型GM(1,1)的参数采用最小二乘法求解,具体内容见文[15].

2 结果分析

2.1 样本描述分析

为了更直观展现指标样本数据的特点与态势,绘制了不同年度指标分析图(图1).结合SPSS 23.0中的“独立样本T检验”等内容,对研究时段内的指标样本数据进行检验与分析,具体内容见表3;其中季节划分采用闫军辉[16]等的方法:3～5月、6～8月、9～11月和12～2月分别为春季、夏季、秋季和冬季.

(1) 近5年新乡市PM10指标的数值为124.983 ± 12.035 μg/m3(95%置信区间,下同).由图1(a)可知,冬季和春季的PM10指标值较高,污染较为严重,除2015年12月份外,其他年际月变化趋势的差异不大;表3中数据显示,冬季和春季的PM10指标数值高于夏季和秋季,与图1(a)结果一致.

(2) 近5年新乡市PM2.5指标的数值为71.517 ± 8.600 μg/m3.由图1(b)可知,历年冬季PM2.5指标值均高于其他季节且差异较大,即污染主要集中在冬季,而年际间月变化趋势的差异不大;表3中冬季的PM2.5指标数值达到了110.533 ± 19.560 μg/m3,接近于其他季节指标值的2倍,验证了图1(b)中的指标分析结果.

(3) 近5年新乡市SO2指标的数值为29.150 ± 4.220 μg/m3.由图1(c)可知,2015年冬季SO2指标值显著高于其他季节,2016年和2017年春季SO2指标值显著高于其他季节,其他年份每月 SO2指标值变化差异不大,总体呈现冬季和春季污染较为严重态势,年际月变化趋势的差异较大,且近3年呈现出趋好态势;通过表3的数据可以看出,该指标值在四个季节中的差异较小,且夏季达到了四季中的最低值为19.133 ±4.100 μg/m3,与图1(c)中展现的结果保持一致.

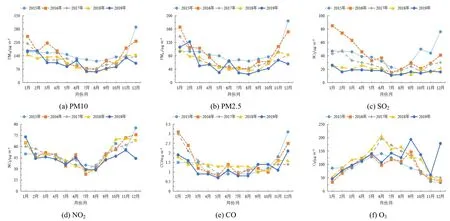
图1 不同年度指标分析

(4) 近5年新乡市NO2指标的数值为48.717 ± 3.565 μg/m3.由图1(d)可知,在秋季和冬季NO2指标值明显高于其他季节,污染较为严重,而年际月变化趋势的差异较小,呈现出相同的趋势;表3中的数据显示,NO2指标值在秋冬季节较高,分别为56.400 ± 5.370 μg/m3和59.867 ± 7.245 μg/m3,而春夏两季 NO2指标数值相对较低,与图1(d)有着相同的趋势.

(5) 近5年新乡市CO指标的数值为1.385 ± 0.142 mg/m3.由图1(e)可知,历年冬季CO指标值居高不下,尤其在2016年和2017年表现较为显著,可知污染主要集中在冬季,年际月变化趋势的差异不大,且近3年呈现出趋好态势;由表3中CO指标数值可知,冬季数值最高达到2.067 ± 0.343 mg/m3,接近于其他季节该指标数值的2倍,且其他季节的指标数值之间差异较小,与图1(e)中的CO指标月份分析趋势一致.

(6) 近5年新乡市O3指标的数值为104.967 ± 11.435 μg/m3.由图1(f)可知,春季和夏季的O3指标值明显高于秋季和冬季,变化曲线呈现出倒“V”的形状,可知春季和夏季污染较为严重,同时年际间月变化趋势的差异较大,且近3年呈现出趋差态势;表3中O3指标数值显示,春夏季指标数值显著高于秋冬两季,且夏季最高达到141.200 ± 18.510 μg/m3,但由图1(f)中可看出2019年O3指标数值异于其他年份的走势,在11月份降到最低值后又突然升高,而其他季节与图1(f)中的变化趋势相一致.

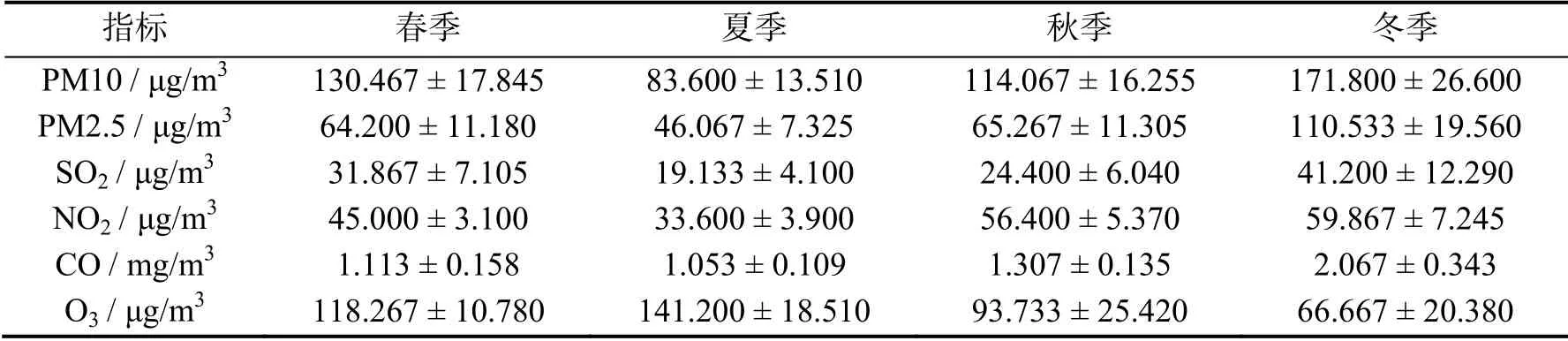
表3 不同季度指标分析

2.2 灰色模糊物元分析

依据式(1)～(3)进行计算,得出2015～2019年年际间月变化趋势分析和不同指标年度分析如图2和图3所示.

由图2可知,2015～2019年这5年间,总体呈现出夏季和秋季的分值高于冬季和春季的态势,说明新乡市这五年间大气环境质量在夏季和秋季均优于其他两季.2015年与其他年份月变化趋势的差异较大,并且在12月份达到了这5年间的最低值,大气环境质量较差.2016～2018年的月变化趋势基本相似,都在7月份达到了一年中的峰值,是大气环境质量最好的月份,2019年的整体分值高于其余年份,并于8月达到了峰值,表明新乡市2019年的大气环境质量优于其他年份.

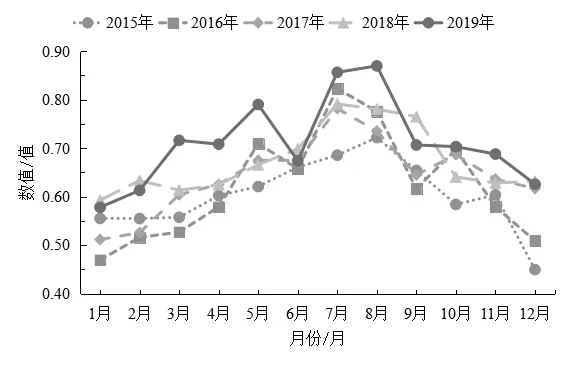
图2 2015～2019年年际间月变化分析

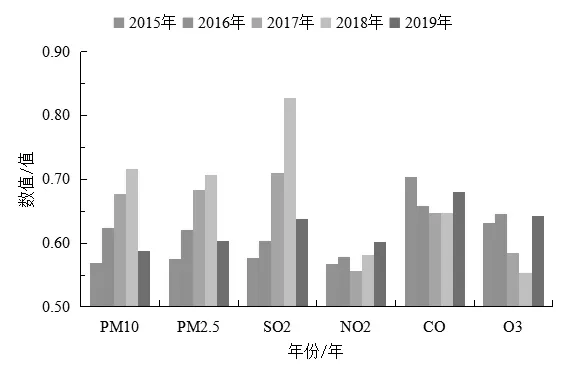
图3 2015～2019年不同指标年度分析

由图3可知,PM10指标分值、PM2.5指标分值、SO2指标分值在2015～2018年均呈现出逐步上升的态势,表明这些指标在大气环境中的含量逐步增加,污染加剧,其中SO2指标分值变化的幅度最大,但在2019年这些指标值均有较大幅度的下降,环境有所好转.NO2指标分值和CO指标分值在这五年间变化幅度较小,态势较为平缓,且NO2指标分值低于其他指标,在大气环境中的含量较为稳定;O3指标分值在2015～2018年呈现出逐步下降的态势并在2018年达到了最低值,但在2019年又迅速回升,波动较大.

2.3 灰色预测分析

通过灰色预测模型得到的分析预测结果见表4.2015～2019年的现状值与预测值之间的相对误差值分别为0.00、2.90%、2.10%、2.10%、2.30%,均低于一般要求,即≤5.00%,这证明了通过灰色预测模型进行分析预测的合理性和可靠性.通过该模型对2020和2021年进行预测,得到预测值分别为0.7608和0.8005,表明新乡市大气环境质量在2020年和2021年有着向好的态势.

表4 灰色预测分析

3 结语

(1) 本文在模糊物元分析的基础上结合灰色预测将其扩充为新的灰色模糊物元预测模型,利用该模型对新乡市2015～2019年大气环境中的6个指标PM10、PM2.5、SO2、NO2、CO和O3进行分析评价和预测,在数据处理时采用了均值法和均方差法,避免了主观因素对预测结果的影响.

(2) 将灰色预测模型得出的不同年份的预测值与现状值进行对比,发现误差值在一般要求之内.实例表明,针对大气环境自身的脆弱性[18]和复杂性[19],灰色模糊物元分析方法在此类评价中切实可行,能够较为准确地对大气环境质量进行分析和预测,解决了多指标分析评价时的不相容问题,借助数学模型和相关算法,能够确保大气环境质量评价预测的客观性及可靠性.

(3) 大气环境质量评价中的灰色模糊物元预测方法实用性较强,同时降低了传统评估预测方法中存在的主观性,此外上述方法的计算过程较为简便,能为研究者提供辅助支持,有着较好的应用前景.后续研究应当考虑将其拓展至诸如农村环境治理[20]、空气质量指数[21]等研究方向.