具有非线性发生率函数的随机SEIR模型性质研究

朱 哲，王 锋

具有非线性发生率函数的随机SEIR模型性质研究

朱 哲，王 锋

（萍乡学院 工程与管理学院，江西 萍乡 337000）

文章研究了一类具有非线性发生率函数的随机SEIR模型的动力学行为，利用随机微分方程理论探讨了随机扰动对模型轨迹的影响，最后列举了一个例子来验证得到的结论。结果表明，随机扰动有利于抑制疾病的发生。

SEIR模型；随机扰动；灭绝性

1 引言

2020年伊始，新冠肺炎疫情在中国暴发，随后肆虐全球，给世界带来了巨大的灾难。当疫情在武汉暴发初期，学者们利用不同传染病模型对感染人数进行拟合和预测[1–2]。传染病模型在疾病的预防和控制中起着重要的作用，因此很多学者研究了不同模型的各类性质[3–5]。Lan等[5]通过研究SIRS模型的性质阐述了医院病床等医疗资源对于疾病控制的重要影响。SEIR模型是传染病模型重要类型之一，它将群体分为易感者类（S），潜伏期类（E），受感染者类（I），恢复者类（R）。带有非线性发生率函数的模型可表达如下：

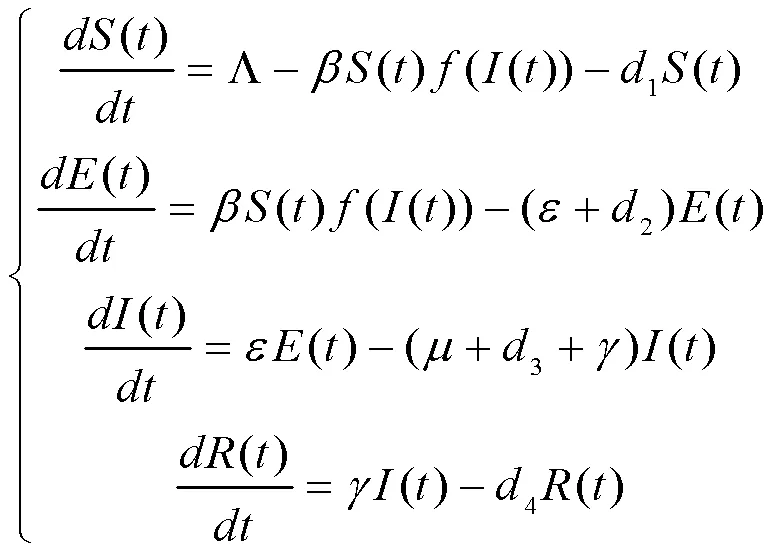
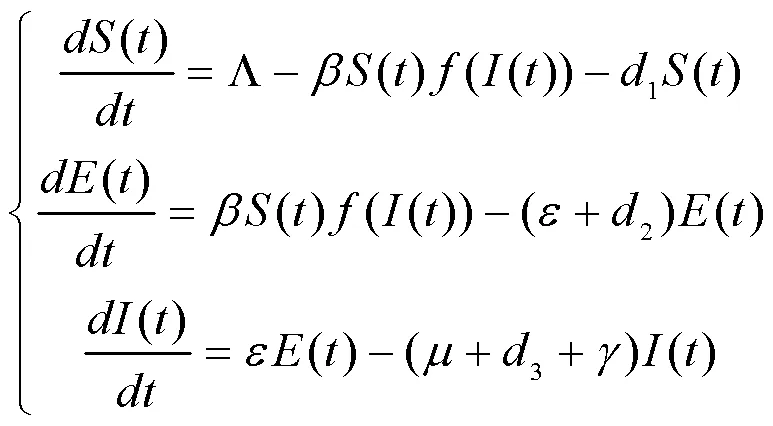
众所周知，生活充斥着各种随机因素，这些随机因素会不同程度的改变事务原本的轨迹。数学中常用布朗运动来刻画这些随机因素[5–6]。本文假设随机扰动为按各群体的比例计，具体形式如下：

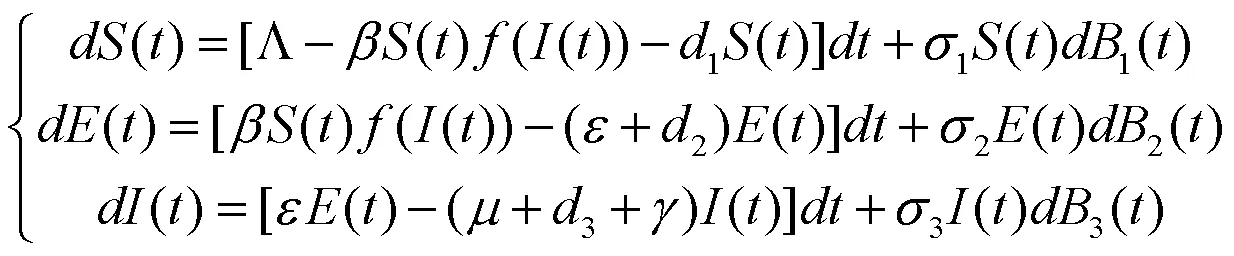
本文将研究随机模型（3）的动力学行为。第2节给出了随机微分方程的一些基本知识，第3节研究了随机扰动对模型行为的影响，第4节举出例子来验证第3节所得结果。

2 预备知识

3 模型（3）的动力行为

这一节将研究疾病灭绝性的条件。

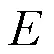
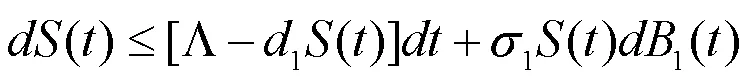
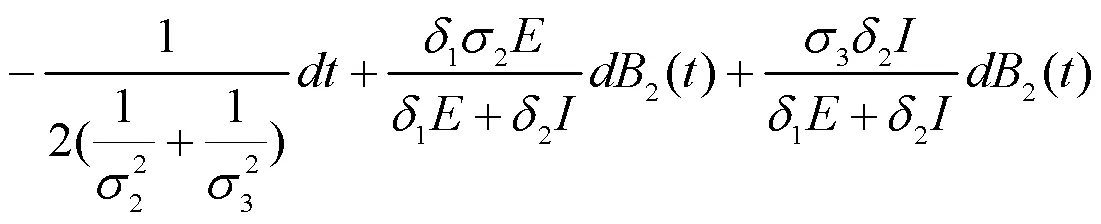
对（6）式从0到积分，并同时除以，得

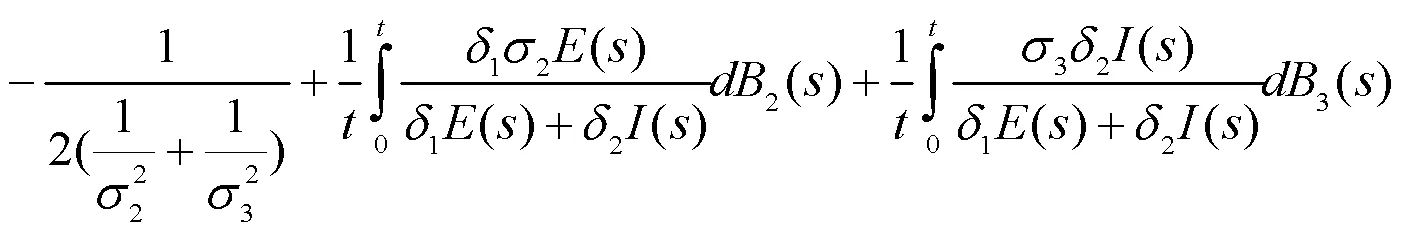
4 数值模拟

这一节将列举例子并给出其轨迹来验证前面所得结论。

图1 例1中确定型模型（2）的轨迹

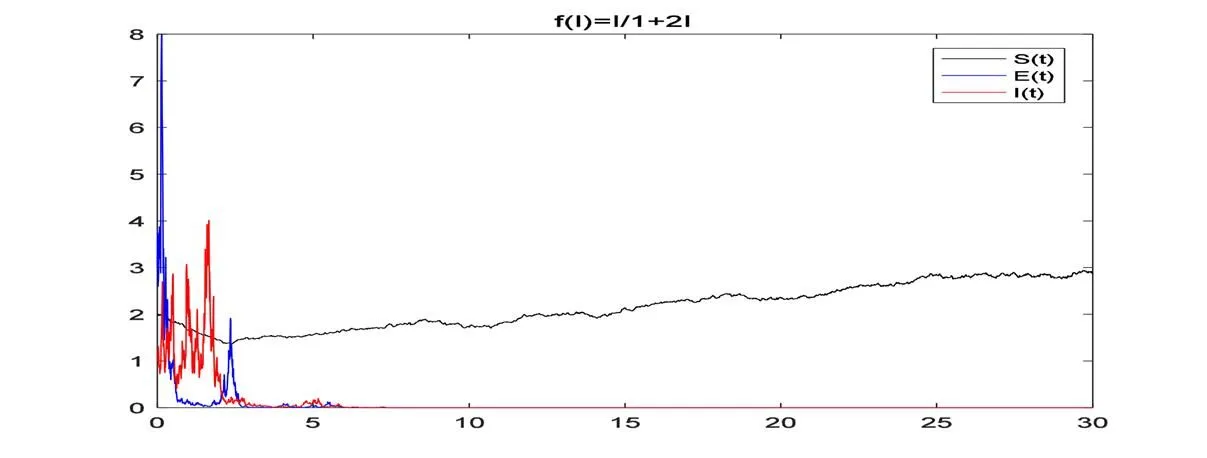
图2 例1中随机模型（3）的轨迹

5 结论

本文研究了一类具有非线性发生率函数的随机SEIR模型的动力学行为，并利用随机微分方程理论探讨了随机扰动对模型轨迹的影响，数值试验的结果表明，随机扰动有利于疾病的灭绝。

[1] 张琳. 新冠肺炎疫情传播的一般增长模型拟合与预测[J]. 电子科技大学学报, 2020, 49（3）:345–348.

[2] 赵序茅, 李欣海, 聂常虹. 基于大数据回溯新冠肺炎的扩散趋势及中国对疫情的控制研究[J]. 中国科学院院刊, 2020, 35（3）：248–255.

[3] Tornatore E., Buccellato S.M., Vetro P.. Stability of a stochastic SIR system[J]. Physica A, 354 (2005):111–126.

[4] Zhang Y , Fan K., Gao S., et al. Ergodic stationary distribution of a stochastic SIRS epidemic model incorporating media coverage and saturated incidence rate[J]. Physica A, 2019, 514: 671–685.

[5] Lan G., Yuan S., Song B. The impact of hospital resources and environmental perturbations to the dynamics of SIRS model[J], Journal of the Franklin Institute 2021, 358: 2405–2433.

[6] Mao X.R. Stochastic differential equation and applications[M] Horwood, Chichester, UK, 1997.

[7] Dreessche P , Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1—2):29–48.

[8] Liu Q., Jiang D , Hayat T , et al. Dynamics of a stochastic SIR epidemic model with distributed delay and degenerate diffusion[J]. Journal of the Franklin Institute, 2019, 356(13):7347–7370.

Study on Properties of Stochastic SEIR Model with Nonlinear Incidence Rate

ZHU Zhe, WANG Feng

(School of Engineering and Management, Pingxiang University, Pingxiang, Jiangxi 337000, China)

The paper studies the dynamic behavior of a class of stochastic SEIR model with nonlinear incidence rate, explores the effects of stochastic perturbations on model trajectories using stochastic differential equation theory, and finally presents an example to verify the obtained conclusions. The results show that the stochastic perturbation is beneficial to suppress the occurrence of the disease.

SEIR model; stochastic perturbation; extinction

O211.6；O29

A

2095-9249（2021）06-0001-05

2020-12-24

江西省教育厅科学技术研究项目（GJJ202713）

朱哲（1990—），男，江西萍乡人，助教，硕士，研究方向：概率统计及应用，金融数学。

〔责任编校：陈楠楠〕