在小学数学教学中落实“以学为中心”的策略


[摘 要] 在新课程改革实施过程中,教师从“以教为中心”转为“以学为中心”。教师对“学”的理解,既要关注学习者本身,又要关注学习本身。笔者从这两个维度阐述“蹲下来”“站起来”“放出去”“收回来”这四个导向,积极探索“以学为中心”的课堂教学路径。
[关键词] 小学数学;课堂教学;以学为中心
[作者简介]胡晓娟(1976— ),女,江苏南京人,南京市陶行知小学,高级教师,研究方向为小学数学教学。
陶行知先生认为,教书先生可分为三种:第一种先生只会教书,只会拿一本书要儿童来读、来记;第二种先生不是教书,乃是教学生,让学生被动地接受教师传授的知识;第三种先生不是教书,也不是教学生,而是教学生学,尊重学生的主体地位,发挥学生的主体作用,而第三种才是我们要做到的。
在新课程改革实施过程中,教师从“以教为中心”转为“以学为中心”。教师对“学”的理解需要关注两个维度:一是学习者本身,即学习者的身体发展、心理发育、认知特点、情感培养等因素;二是学习本身,即以动态的视角关注学生的学习过程,评价学习结果。基于上述分析,结合案例,笔者谈谈如何在小学数学课堂教学中落实“以学为中心”。
一、蹲下来——理解儿童
案例一:苏教版《数学》二年级下册“角的初步认识”
活动一:摸一摸
师:同学们,生活中有很多种角,你在哪些物体上看到了角?请你摸一摸,并说出你的感受。
生1:我在数学书上看到了角,我觉得角是直直的、尖尖的。
生2:我在黑板上看到了角,我觉得角是平平的、直直的、尖尖的。
师:同学们都有共同感受,认为角是直直的、尖尖的。
活动二:描一描
师:请你利用手中的物体,描出一个角来。
师:观察我们描出的角,你们发现直直的是什么?尖尖的又在哪里?
(引导学生明确,直直的是角的两条边,尖尖的是角的顶点)
活动三:画一画
师:现在请同学们借助直尺,画一个角,注意体现出角的两条边和一个顶点。
活动四:拨一拨
师:钟表上面也有角,你们发现了吗?
(展示钟表,让学生拨到1,指出此时角的顶点和两条边)
师:当指针拨到2时,与之前的角对比一下,你们有什么发现?拨到3、4、5时,你们又发现了什么?
(引导学生明确角的度数在变大)
师:现在不让你们拨钟面了,只让你们在脑袋中想一想,要想这个角的度数变大,你打算怎么做?如果把这个角的度数变小呢?
生3:把两条边靠拢一些。
生4:让两条边分开得更大一些。
(引导学生明确,角的大小确实与两条边张开的角度有关)
“角”对于学生而言,是一个既陌生又熟悉的概念。教师需要掌握学生的学情,了解其所知,分析其需知,强化其应知。从“摸一摸”活动中提取生活原型,在“描一描”活动中体现数学表征,再到“画一画”活动中概括图形特征,最后到“拨一拨”活动中回归生活,运用知识解释现象,发现问题,解决问题。
二、站起来——立足发展
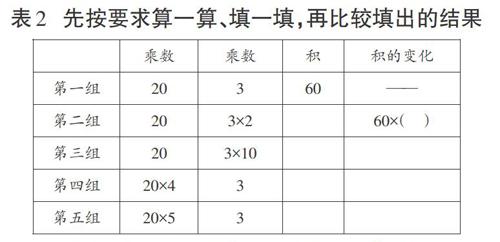
案例二:苏教版《数学》四年级下册“积的变化规律”
A设计:
师:同学们完成以下表格,比一比乘数有什么变化?积有什么变化?你还能接着举例吗?
生1:当20不变时,假设3×4,那么积是240,积的变化是60×4。
师:你们能概括一下发现的规律吗?
生2:一个乘数不变,另一个乘数乘以几,积就乘以几。
B设计:
师:同学们先填写表格,然后按照老师给出的三个问题,展开学习。
问题①:观察表中算式,是否存在一定的规律?说说你的猜想。
问题②:如何验证你的猜想?
问题③:你的结论是什么?
师:我们发现,一个乘数不变,另一个乘数乘以几,积也乘以几。大家是否还能提出新的猜想?
生1:一个乘数不变,另一个乘数除以几,积也除以几。
生2:一个乘数不变,另一個乘数加几,积会不会也加几?
生3:一个乘数乘以几,另一个乘数也乘以几,积会怎么样呢?
师:选择你们想研究的问题,像刚才那样验证,再来汇报你们的结论吧!
A设计涉及指令式问题,学生独立思考、自主探究的空间明显不足;B设计更关注对同类问题的引导,以教学为范例,指导学生深入研究。所以在教学实施中,更应推广B设计。
三、放出去——鼓励交流
案例三:苏教版《数学》六年级下册“圆柱的表面积”
①要求学生在方格纸上画出底面半径1厘米、高2厘米的圆柱展开图。
②分组交流:说说画出的圆柱展开图有什么不同?有什么相同?
③汇报反馈。
生1:圆柱的展开图都有两个半径为1厘米的圆形,还有一个长方形,长为2π厘米,宽为2厘米。
生2:不同之处在于,两个底面的位置不同。所以,我觉得左图不对,两个底面不应该在同一侧。
生3:我认为左图是对的,借助黏合剂就行了。两个底面的位置可以在一起。
生4:我觉得从节省材料的角度来考虑,左图可能更节约,两个底面凑在一起,挺节省材料的。
学习既是内化的过程,又是运用的过程;既是个体建构的过程,又是相互分享的过程。在交流中,学生能学会表达自己的观点,倾听他人的想法,在讨论中达成共识。教师需要根据教学目标,设计教学活动,强化学生合作学习的意识和能力。
四、收回来——专业引领
案例四:苏教版《数学》六年级下册“圆柱的体积计算”
师:给这一零件(如图3所示)涂色,需要涂色的面积是多少?
生1:分别求出两个圆柱的表面积,再减去两个小圆柱的底面面积。
生2:求出大圆柱的表面积,再求出小圆柱侧面的面积,最后相加。
师:两种解法都是对的,比较一下,哪种解法更加简便呢?
拓展:计算如图4所示的组合体的表面积。
小学生的思维水平会随着知识结构和认知水平而不断发展,是一个动态提升的过程。在这一过程中,教师的专业引领至关重要。从学科角度引导学生深度学习,从认知角度发展学生的思维能力,是教师应该“收回来”的责任。
综上所述,“以学为中心”即以学习者为中心,立足学生的发展,鼓励学生交流。教师应该以学生的“学”为中心,从专业视角、教育高度,引领学生全面发展。

