钢筋混凝土异形柱下独立基础验算程序研究*

孔子昂， 徐秀凤， 任传尧， 贾海涛， 王正云， 周 强

(1 浙江绿城建筑设计有限公司青岛分公司， 青岛 266071； 2 青岛黄海学院建筑工程学院， 青岛 266427; 3 青岛杰地建筑设计有限公司， 青岛 266071)

0 引言

在合院项目设计中，若采用矩形柱作为竖向受力构件，其往往会暴露在墙体之外，影响家具摆放，减小室内使用面积，不能满足人们对建筑审美和使用功能上的需求。同时，在某些位置，由于门窗洞口的限制，难以布置剪力墙，这时就需要采用异形柱作为替代和补充，异形柱能够有效地提升框架结构房屋的有效使用面积，尤其方便家庭装修，受到了房屋开发商和用户的青睐[1-2]。2017年12月1日正式实施的《混凝土异形柱结构技术规程》(JGJ 149—2017)[3](简称《异形柱规程》)进一步明确了异形柱的设计方法和原则，并增加了Z形柱的相关规定，同时提出楼梯间和电梯井也可以采用肢端设暗柱的异形柱，极大地扩展了异形柱的使用范围。

但是，目前异形柱下独立基础的设计在《建筑地基基础设计规范》(GB 50007—2011)[4](简称《地规》)等相关规范中没有明确规定，传统的辅助设计软件，如PKPM工具箱、Morgain等均不具有异形柱下独立基础的验算功能。虽然，理正工具箱在7.0以后版本中推出了相关功能，但在验算方法和原则方面存在诸多问题。同时，由于柱下独立基础局部破坏的特点[5]，手算工作量大，易出错，且难以形成计算书供他人检验，这使得异形柱下独立基础的设计一直是异形柱结构设计中的痛点和难点[6]，因此急需一款能够对异形柱下独立基础进行验算的程序。

本文结合中国《地规》、美国规范ACI 318-08[7]的相关规定，介绍了异形柱下独立基础的剪切和冲切承载力验算方法，对存在零应力区时的基底反力进行了分析，并采用AutoLISP语言开发了钢筋混凝土异形柱下独立基础验算程序，此程序可与AutoCAD软件进行窗口交互，自动进行冲切和剪切承载力的验算并生成计算书，为验证此程序的正确性，分别采用本文开发的程序、理正工具箱(7.0PB5版)、YJK(1.9.3版)等三种软件，并依据美国规范ACI 318-08相关规定，对L形、T形、十字形、Z形柱下独立基础算例进行了对比分析。

1 已有柱下独立基础验算程序现状研究

现行的结构设计软件中仅有YJK和理正工具箱7.0以后版本可对异形柱下独立基础进行验算，其中YJK(1.9.3版)将异形柱简化成外包矩形柱进行验算，设计方法过于简略。

理正工具箱(7.0PB5版)虽可验算矩形柱、圆形柱及异形柱(L形、T形、工字形、槽形、十字形)下的单柱和双柱基础，适用范围较广，但在验算异形柱下独立基础时存在一定的问题，如：将受冲切验算分为“整体破坏模式”验算和“局部破坏模式”验算(图1)，而我国《地规》在验算独立基础时，并不存在“整体破坏模式”，该种破坏模式仅在柱对板或筏板的冲切中需要验算。另外，“整体破坏模式”的计算方法有误，其公式仍采用《地规》第8.2.8条中独立基础的冲切验算公式，仅在计算冲切周长时与“局部破坏模式”有所区别，这种计算缺乏理论与试验根据，如需计算“整体破坏模式”，应按照柱对板或筏板的冲切计算方法进行计算。同时，理正工具箱(7.0PB5版)假设了两种破坏形态(图2)，其中“真实截面”破坏形态不合理，其与《地规》和美国规范ACI 318-08假定的破坏形态和试验结果均不相符。此外，冲切力的计算不符合《地规》第8.2.8条的规定，仅采用冲切阴影区域内的冲切力而未采用冲切基底净反力最大值乘以冲切阴影面积，降低了基础的安全储备。最后，理正工具箱(7.0PB5版)没有验算柱边宽高比的功能。

图1 理正工具箱(7.0PB5版)采用的两种破坏模式

图2 理正工具箱(7.0PB5版)采用的两种破坏形态

2 异形柱下独立基础验算方法

本文开发的异形柱下独立基础的验算程序可对《异形柱规程》规定的L形、T形、十字形和Z形四种异形柱(图3)下独立基础进行验算。

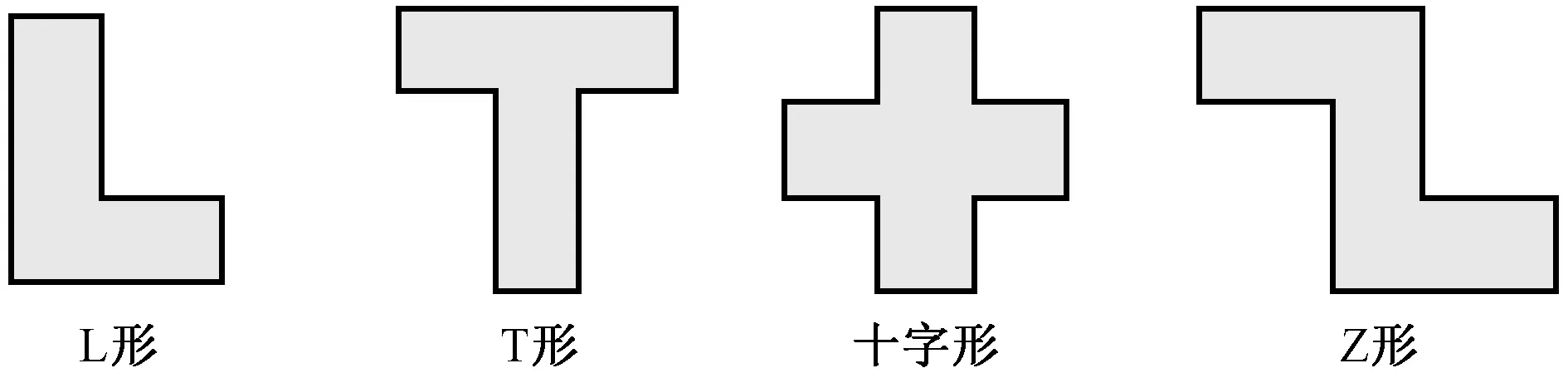
图3 异形柱的四种形状

2.1 受冲切截面及受剪切截面的确定

本文程序将冲切破坏锥体的斜截面作为受冲切截面；抗剪切截面定义为通过有效加载面各边且贯通整个基础截面的平面。此程序中有效加载面、临界截面和冲切锥底面参考美国规范ACI 318-08确定，即将异形柱外凸角点依次相连得到的多边形围成的截面定义为有效加载面，将此有效加载面向外偏移0.5h0(h0有效截面高度)得到临界截面，向外偏移h0得到冲切锥底面轮廓。四种异形柱的有效加载面、临界截面及冲切锥底面如图4所示。

图4 异形柱有效加载面、临界截面及冲切锥底面

图5 基础底面存在零应力区的三类情况

2.2 异形柱下独立基础的冲切和剪切验算方法

异形柱下独立基础冲切承载力和剪切承载力按式(1)和式(2)进行验算[2]：

(1)

(2)

式中各参数的含义参见《地规》第8.2.8条和第8.2.9条的有关规定。

根据《地规》的规定，柱下独立基础的冲切破坏模式为局部破坏模式，即在验算过程中，需要对冲切破坏锥体的最不利斜截面进行验算。由于最不利斜截面不宜确定，本文程序验算有效加载面每一条边所对应的受冲切及受剪切截面是否满足承载力要求，只有当所有截面均满足承载力要求时，基础才满足要求。

2.3 零应力区验算

《建筑抗震设计规范》(GB 50011—2010)[8](简称《抗规》)规定，“高宽比大于4的高层建筑，在地震作用下基础底面不宜出现脱离区(零应力区)；其他建筑，基础底面与地基土之间零应力区面积不应超过基础底面积的15%”。本文程序中也包含零应力区的验算。下文详细介绍当双向受弯基础的基底存在零应力区时的基底反力分布的计算方法。

当双向受弯基础的基底存在零应力区时，基底反力的分布存在三类情况[9]：第一类情况(情况A)，基础底面大面积与地基脱开，基础有三个角点应力为0，基底反力在空间中的形状为四面体，在基础底面的投影为直角三角形，其形心在基础底面的投影坐标为(ex，ey)，与三角形的形心重合，如图5(a)所示。此时直角三角形的两直角边，应分别小于相应基础边的边长。即：

(3)

由图5(a)可知情况A无法满足《抗规》要求，若在计算中出现此情况，本文程序将提示设计人员重新设计基础尺寸。

第二类情况(情况B和情况C)，基础底面与地基部分脱开，基础有两个角点应力为0，基底反力在空间中的形状为平放的三棱台，如图5(b)和图5(c)所示。以图5(c)所示情况C为例，根据三棱台的体积等于轴力，形心在基底的投影坐标为(ex，ey)，可得如下方程：

(4)

式中：pmax为基础边缘处最大地基土单位面积净反力；N为柱的轴力。

ey所在方程为l1的二次方程，首先对其求解，可以求解整个方程组，即：

(5)

同理，对于图5(b)所示情况B，方程组为：

(6)

方程的解为：

(7)

第三类情况(情况D)，基础只有一个角点应力为0，基础反力在空间中的形状为切掉一角的三棱台，如图5(d)情况D所示。根据力的平衡关系及几何关系，可以得到如下方程：

(8)

该方程组为二元四次方程，难以直接求解，本文程序采用Newton法[10]通过迭代函数对其进行数值求解，求解方法如下：

(9)

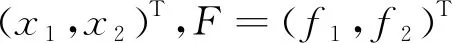
F(X)≈F(X(k))+F′(X(k))(X-X(k))

(10)

其中：

(11)

可得迭代方程：

(12)

其中：

(13)

非线性方程组一般有多个解，当选择不同初值时，Newton法可能会收敛到不同的解，这就要求初值与真值之间不能相差过大。实践表明，当初值选择由式(14)计算得到的值时，Newton法能够很好地收敛到真实解。

(14)

2.4 零应力区面积比验算公式

通过计算不同偏心距比下的基底零应力区面积比，可得到临界状态(零应力区面积比接近但小于0.15的状态)下两个方向偏心距比的关系，如图6所示。

图6 数值分析点组成的临界曲线及其拟合曲线

(15)

经数值计算验证，当两个方向的偏心距比满足式(15)时，基础的零应力区面积一定小于基底面积的15%。式(15)为设计人员快速布置基础提供了依据，大大简化了设计过程。

2.5 柱边宽高比判断

柱边宽高比定义为柱边到对应的基础边的距离与基础高度的比值。本文程序对异形柱的外包矩形进行验算，当外包矩形柱各边的柱边宽高比均小于等于2.5时，则认为异形柱下独立基础具有足够的刚度，使得基底反力呈直线分布的假设成立。

3 异形柱下独立基础验算程序

3.1 程序简介

本文研发的异形柱下独立基础验算程序采用AutoLISP语言编制，可与AutoCAD软件窗口交互，如图7所示，在输入荷载及独立基础的信息后对基础进行验算并生成计算书。

图7 本文程序与AutoCAD软件的交互窗口

程序适用于柱形状为矩形或四种异形柱(图3)的一阶阶梯形矩形单柱基础，基础的形心与柱的形心可不重合。柱的轴线(或边长)与基础的轴线(或边长)相平行，即不存在柱相对于基础的旋转。

3.2 程序模块说明

程序分为可视化输入、计算及结果输出三大模块，三个模块之间、子块和子块之间的逻辑关系如图8所示。

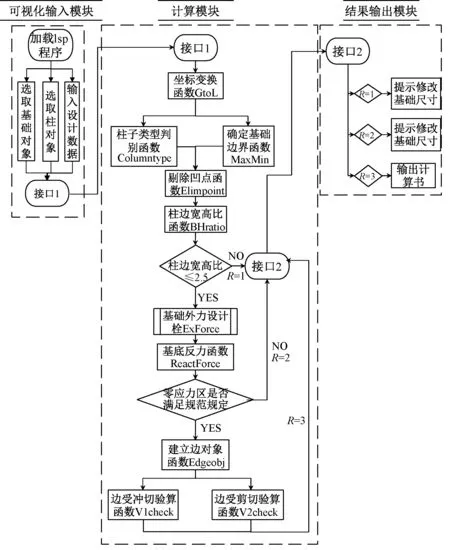
图8 本文程序流程图

可视化输入模块的功能在于，提示设计人员点选柱、基础的图形对象。通过对话框的形式，要求设计人员输入基础的高度，通过柱形心的轴力、弯矩和剪力的设计值，混凝土强度等级，以及基础顶面的埋置深度，将这些数据传递给计算模块。并告知设计人员程序的适用范围以及所采取的假设。

计算模块的功能在于，将整体坐标系下柱和基础节点坐标转换为以基础形心为原点建立的局部坐标系坐标；根据输入模块传入的数据，验算各柱边宽高比；计算通过基础形心的轴力、弯矩的设计值；计算基底应力分布，给出阴影区域范围内的基底净反力最大值以及基底净反力平均值，当存在零应力区时，计算零应力区面积；验算零应力区是否满足2.3节的规定；验算有效加载面各边是否满足冲切和剪切承载力要求；将输出的结果传递给结果输出模块。

结果输出模块的功能在于，根据计算模块传入的数据，输出txt格式的计算书。输出的计算结果包括基础和柱尺寸、外力设计值、钢筋和混凝土的材料信息、柱形心的局部坐标、基底反力最大值和平均值及最小值或零应力区面积比，以及各边冲切及剪切承载力的验算过程，并在计算中提示设计人员基础设计中存在的问题。

在以上三大模块中，加入了很多提示和报错功能，可以帮助设计人员了解程序所处的状态，这使得整个程序易于上手。

3.3 程序中相关函数简介

程序流程图(图8)中所应用到的主要函数功能如下：

(1)坐标转换函数GtoL。该函数以矩形基础为基准建立局部坐标系，以基础形心为原点，以通过形心平行于基础边的直线为轴，将基础及柱在整体坐标系中的坐标转换为局部坐标。当局部坐标系相对于整体坐标系逆时针旋转θ⊂(0,π)，局部坐标系原点在整体坐标系中的坐标为(x0，y0)时，可以得到局部坐标系(x′,y′)与整体坐标系(x,y)之间的关系为：

(16)

若局部坐标系相对于整体坐标系顺时针旋转θ⊂(0,π)，将-θ代入，可得转换关系为：

(17)

(2)柱类形判别函数Columntype。该函数用于判定柱的种类，为后续计算提供数据。

(3)确定基础边界函数。通过函数MaxMin确定基础顶点坐标，为后续计算的判定提供依据。

(4)剔除凹点函数Elimpoint。用于剔除异形柱的凹点，求得有效加载面顶点坐标，以此为基础进行各边的受冲切和受剪承载力计算。

(5)柱边宽高比函数BHratio。用于计算与判断异形柱外包矩形柱的柱边宽高比是否小于等于2.5。若不满足将终止程序，并提示设计人员重新设计基础尺寸。

(6)外力设计值函数ExForce。用于将柱形心处的外力系转换为基础形心处的外力系，通过基础埋深与剪力的乘积考虑由剪力引起的附加弯矩。

(7)基底反力函数ReactForce。用于计算基底反力的分布，给出基底反力最大值、基底反力平均值、零应力区面积等三个值，用于后续计算。若零应力区的面积不满足《抗规》要求，则结束程序，提示设计人员重新设计基础尺寸。

(8)边对象函数Edgeobj。以有效加载面积的各边为对象，计算其对应的受冲切截面面积、冲切阴影面积、冲切标记(是否需要冲切验算的记号)、受剪切截面面积、剪切阴影面积等五个数据，将这些数据传递给边受冲切验算函数V1check和边受剪切验算函数V2check，进一步验证各边是否满足承载力要求。

4 程序验证

为了验证本文开发的程序的合理可靠，分别采用本文程序、理正工具箱(7.0PB5版)、YJK(1.9.3版)，并依据美国规范ACI 318-08的相关规定，对四种形状的柱下独立基础进行了承载力计算。假设所有基础为正方形，基础形心与柱形心重合，且弯矩引起的两个方向的偏心距比均为0.1，其余信息如表1所示。计算结果如表2所示。

采用理正工具箱(7.0PB5版)时，参数“冲切计算截面形式”选择“外包截面”，参数“基底反力选用值”选择“最大值”来计算控制轴力，这表示采用阴影区域最大反力乘以阴影区面积计算外力。与《地规》计算方法相比，采用此方法时，剪力计算偏于保守，因此当基础承载力由剪切控制时，计算得到的控制轴力也较小。

四种异形柱下独立基础算例 表1

不同计算方法结果对比 表2

美国规范ACI 318-08中基础的剪切承载力Vc1、冲切承载力Vc2和最大冲切剪应力υmax分别由式(18)、式(19)和式(20)决定，剪切控制面在距离柱边0.5d处。

(18)

(19)

(20)

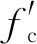
当基础厚度不变时，临界截面重心的位置(xcg,yxg)由式(21)决定：

xcg=∮xdl/b0,ycg=∮ydl/b0

(21)

以x轴受弯为例，由附加弯矩引起的剪应力分布如图10所示。从图中可看出，剪力传递的附加弯矩由竖向剪应力和水平剪应力共同承担，其中竖向剪应力的大小与y成正比，水平剪应力绕临界截面的各平面水平轴中心对称，且斜截面与竖向截面的曲率存在如下关系：

sinα′/sinβ′≈α′/β′=cosθ′

(22)

因此，斜截面的类极惯性矩为相同尺寸的竖向截面的cos2θ′倍。

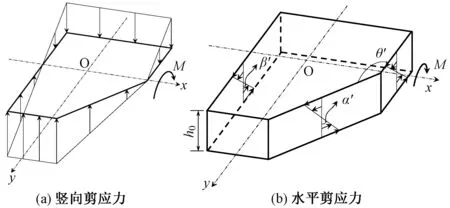
图10 由附加弯矩引起的剪应力分布

在计算中发现，YJK(1.9.3版)将异形柱转换为外包矩形柱进行验算，且在计算外力时，一律采用“真实值”，即外力等于阴影区反力平均值乘以阴影区面积，因此冲切验算结果偏不安全；同时YJK(1.9.3版)自动执行《地规》第8.2.9条：当基础尺寸大于柱宽加2h0时，不进行剪切验算。当采用理正工具箱(7.0PB5版)计算，参数“冲切计算截面形式”选择“外包截面”，参数“基底反力选用值”依次选择“最大值”和“真实值”，分别验算冲切承载力和剪切承载力时(需计算两次)，得到的结果与本文程序所计算的结果完全一致。

由表2可知，YJK(1.9.3版)计算的控制轴力明显偏大，采用其计算结果进行设计，基础偏不安全。当基础承载力受冲切控制时，理正工具箱(7.0PB5版)的计算结果与本文程序完全一致；当受剪切控制时，理正工具箱(7.0PB5版)计算结果较为保守，且理正工具箱(7.0PB5版)无法对Z形柱下独立基础进行计算。以本文程序计算结果为基准，等面积方法计算得到的L形、十字形、T形、Z形柱下独立基础的控制轴力的相差百分比分别为14.6%，5.5%，-2.0%，-28.0%，这说明等面积方法计算的结果既可能偏于保守也可能偏于不安全，因此在采用等面积方法进行简化计算时，应对基础尺寸留有余地。采用美国规范ACI 318-08计算得到的L形、十字形、T形、Z形柱下独立基础的控制轴力相对于本文程序计算结果的相差百分比分别为3.3%，26.6%，-3.0%，-6.1%，除十字形柱下独立基础计算结果较为保守外，其余结果与本文程序的计算结果接近，从侧面验证了本文程序的可靠性。

5 结论

(1)本文程序根据中国《地规》及美国规范ACI 318-08的相关规定，确定了L形、T形、十字形、Z形异形柱下独立基础的受冲切、剪切验算截面，以及截面冲切、剪切承载力计算公式。本文程序通过保证异形柱外包矩形的宽高比小于等于2.5，使得独立基础具有足够的刚度，为进一步计算基底反力提供依据。鉴于实际情况的复杂性，本文程序可验算有效加载面各边对应的截面是否满足承载力要求，以保证基础设计的安全可靠。本文程序的验算原则和方法简单合理清晰明了，具有很强的操作性，采用本文程序进行验算能够保证异形柱下独立基础安全可靠，且可使基础设计更加经济。

(2)本文程序可与AutoCAD图形文件互动，自动读取柱及基础信息，使设计人员在绘图的同时即能对基础进行验算，节约了设计时间。本文程序提供的计算书清晰明了，可供设计人员进行校对。本文程序能够适用于各种情况的异形柱下独立基础的承载力验算，也可用于形状类似的墙下独立基础的承载力验算。

(3)本文程序通过数值方法可准确计算当基底存在零反力区时双向受弯基础反力分布。且计算发现，当基础两个方向偏心距比的平方和小于等于0.046 9时，基底零应力区面积一定不超过基底面积0.15倍。该条件使得工程师可直接通过两个方向的偏心距比初步选择基础尺寸，减少了试算次数，优化了设计过程。

(4)采用本文程序与法对四种异形柱下独立基础进行对比计算。结果表明：由于YJK(1.9.3版)采用真实反力进行设计，因此得到的结果明显偏不安全；当理正工具箱(7.0PB5版)采用“外包截面”的破坏模式，并依次采用“最大值”和“真实值”分别计算冲切和剪切承载力时，与本文程序的计算结果一致，但需要进行两次运算；此外，理正工具箱(7.0PB5版)所采用的“真实截面”破坏形态与实际破坏模式不符，且无法验算Z形柱下独立基础；采用等面积方法进行简化计算时，应对设计结果留有余地；本文程序与美国规范ACI 318-08的计算结果相近，从侧面验证了本文程序的安全可靠。