基于声固耦合算法的塔釜持液塔器湿模态分析

李俊儒

（中石化宁波工程有限公司上海分公司，上海 200030）

自振周期的计算是塔式容器设计中的一项重要内容，其准确性直接影响着塔器动力学特性分析的可靠性。对于塔釜持液的塔器，它们在发生振动时会带动内部流场产生变化，而流场的变化又会反过来影响塔器的振动特性，形成了反馈的流体-结构相互作用的流固耦合[1]，此类结构的模态称之为湿模态。与之相对，不考虑流体的影响则称之为干模态。

湿模态是储液容器动力学特性的真正表征[2]，进行湿模态分析是防止此类结构发生共振的基础。目前，在海底管道[3]、发射装置模拟试验承压结构[4]等其他行业的湿模态分析中，多借助有限元软件进行流固耦合或声固耦合分析。其中，采用声固耦合算法处理流固耦合的问题较为简便、高效，其主要思路是将结构中的流体看作声学介质，仅需考虑流体体积应变的压力，不考虑流体的黏性力。当结构振动时在流固交界面上对流体产生负载，同时声压会对结构产生一个附加力[2]。

本文以一高径比H/D＞15 且高度H＞30 m 的等直径等厚度高振型塔器为例，塔器参数如图1 所示，采用有限元软件对塔釜持液塔器进行了基于声固耦合算法的湿模态分析，比较了湿模态与空塔干模态及现行标准NB/T 47041《塔式容器》[5]计算方法结果的差异，并指出了这种差异对于防止塔器出现横风共振的影响。

图1 塔器参数Fig.1 Tower parameters

1 分析模型

图1 所示塔器的内直径2 400 mm，筒体长度69 500 mm（T.L.线至T.L.线），裙座高度3 800 mm，塔器壳体及裙座名义厚度22 mm，腐蚀裕量为3 mm，设备总高73 922 mm，底部持液高度为h。该塔器的设计工况、载荷、材料等其他设计条件同《NB/T 47041—2014＜塔式容器＞标准释义与算例》[6]中的例3。

简便起见，在有限元仿真分析时只对裙座、筒体、流体区域建立模型，不考虑管口、内件、保温层、裙座防火层等附件，如图2 所示。需要说明的是，为了展示流体区域，图2 中筒体、裙座仅显示一半，实际分析时为全模型。

图2 分析模型Fig.2 Analysis model

仿真分析时，钢材密度取等效密度，等效密度ρe等于塔器的操作质量除于金属壳体体积[7]。空塔质量为101 867 kg，金属壳体体积约为10.77 m3，等效密度ρe为9 454 kg/m3。钢材的弹性模量取2×1011Pa，泊松比为0.3。

流体区域定义介质密度和声速两个参数即可，本文介质为水，密度为1 000 kg/m3，声速取1 670 m/s。

湿模态分析时模型的载荷、边界条件为：输入重力加速度，用于模拟液体晃动；裙座底部施加全约束；流体区域上表面定义为自由表面；流体与壳体接触的表面定义为流固界面。

另外，因预应力对结构自振特性的影响不明显，可以忽略，故无需事先进行静力分析。

2 空塔干模态及模型可靠性验证

在进行湿模态分析之前，为了掌握比较基准并验证分析模型的可靠性，先对不持液（即h= 0 mm）的空塔进行模态分析（此时为干模态），并与过程设备设计计算软件SW6（即NB/T 47041 附录B 矩阵迭代法）的计算结果进行比较。

因为塔釜没有液体，故有限元分析时需“抑制”分析模型中的流体区域。此外，在裙座底部施加全约束即可，无其他载荷和边界条件。

有限元和SW6 二者计算结果见表1，从表1 可以看出，两种方法的计算结果误差很小，各阶固有频率最大误差不超过2%。有限元分析得到的各阶频率及相应振型见图3，各阶振型与文献[6]的理论分析一致。这说明了本文分析模型是可靠的。

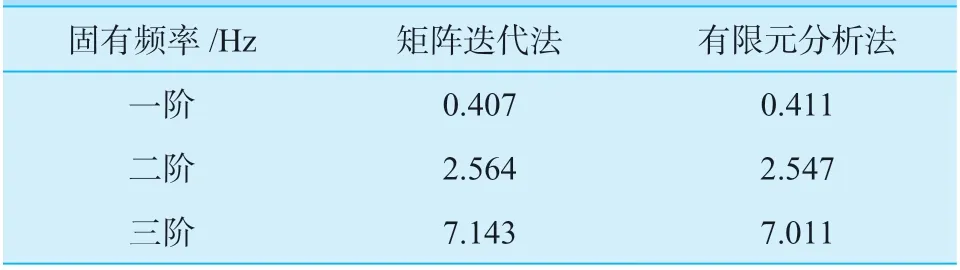
表1 空塔固有频率Table 1 The natural frequency of empty tower

图3 空塔干模态Fig.3 The dry mode of empty tower

3 湿模态分析

若干不同持液高度h（其中包括封头内曲面深度600 mm）的塔器湿模态前三阶固有频率见表2，从表2 可以看出：

表2 不同h 塔器湿模态固有频率Table 2 The natural frequency of wet mode of tower at different h

（1）h≤30 600 mm 时，持液高度的变化对塔器的前三阶固有频率影响较小；

（2）h= 800 mm 时，二阶、三阶固有频率最小；

（3）2 600 mm ≤h≤30 600 mm 时，持液高度的变化对塔器固有频率几乎没有影响；

（4）h= 30 600 mm 时，一阶固有频率略有下降；

而空塔干模态前三阶固有频率分别为0.411 Hz、2.547 Hz、7.011 Hz。比较发现，与干模态相比，湿模态的一阶固有频率几乎不变，但二阶、三阶固有频率下降得较多。以h= 5 600 mm 为例，湿模态二阶、三阶固有频率分别仅为干模态的24.2%和11.3%，振型如图4 所示。从图中可以看出，湿模态一阶振型与空塔干模态类似，最大振幅出现于塔器顶端。但二阶和三阶则不同，它们的最大振幅出现在流体区域的上部，二阶振型为两个对称的环向波，三阶为四个凹凸相间的环向波。塔釜积液不仅大幅度降低了塔器的高阶（二、三阶）固有频率，还改变了振型。

图4 h=5 600 mm 时塔器湿模态Fig.4 The wet mode of tower at h =5 600 mm

4 NB/T 47041方法的讨论

标准NB/T 47041 在计算塔器的自振周期时，仅将介质质量作为操作质量的一部分，与筒体、裙座、内件、保温、平台扶梯等“同等对待”，若介质为液体，则无法考虑其与壳体的流固耦合作用。

为比较NB/T 47041 方法与湿模态计算结果的差异，“抑制”有限元分析模型的流体区域，仅保留裙座和壳体组成的固体区域，并将塔釜持液高度h 范围内的液体质量计入该范围内的金属壳体等效密度。

以h= 5 600 mm 为例， 塔釜持液重量约为24 600 kg，金属壳体体积为0.86 m3，叠加到原有的金属壳体等效密度（ρe= 9 454 kg/m3）之上，得到h= 5 600 mm 范围内金属壳体“新的”等效密度为38 059 m3。计算得到的前三阶固有频率分别为0.411 Hz、2.542 Hz、6.917 Hz，如图5 所示。与湿模态的固有频率相比，一阶近乎相等，但二阶、三阶相差较大，见表3。另外，NB/T 47041 方法与空塔干模态的固有频率相差很小，一阶近乎相同，二阶相差不超过0.3%，三阶相差不超过1.5%。

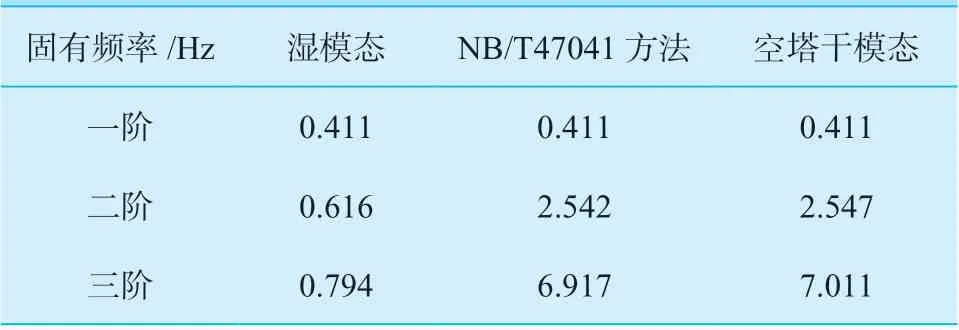
表3 h=5 600 mm 时不同方法计算得到的塔器固有频率Table 3 The natural frequency of tower calculated by different methods at h=5 600 mm

图5 h=5 600 mm 时NB/T 47041 方法计算得到的模态Fig.5 The mode calculated by NB/T 47041 method at h = 5 600 mm

可见，若按NB/T 47041 的方法，几乎看不出塔釜储液对于塔器固有频率的影响，这显然与事实不 符。

5 准确计算固有频率的重要性

对于高径比H/D＞15 且高度H＞20 m 的塔器，NB/T 47041 要求考虑高振型的影响，若H＞30 m还应计算横风向振动。横风向振动由卡门涡街引起，若旋涡脱落频率与塔器的任一阶固有频率一致时就会发生共振，会危及塔器的操作性能和安全性[8]。所以，横风振动是大型塔器设计时关注的重点，必要时应采取适当的减振措施。

共振时的风速称为临界风速，若塔顶风速大于某阶的临界风速，就应考虑该阶及其之前各阶的共振。而临界风速与自振周期成反比，即与固有频率成正比，固有频率越低就越容易发生共振。

对于塔釜持液的塔器，湿模态才是其动力学特性的真正表征。如果采用NB/T 47041 中的方法计算其固有频率，与湿模态分析结果相比，其二阶、三阶的值偏大，会导致“漏判”共振，导致设计偏于不安全。

因此，对于塔釜持液的塔器及其他盛装液体的裙座支撑式容器，应采用有限元分析手段进行准确的湿模态分析。

6 结束语

本文以一直径为2 400 mm、总高为73 922 mm的高振型塔器为例，建立有限元分析模型，进行了基于声固耦合算法的塔釜持液时的湿模态分析，分析表明：塔釜储液大幅度降低了塔器的高阶（二、三阶）固有频率及相应的共振临界风速，还改变了振型。

若按现行塔器标准NB/T 47041 的方法计算此类塔釜持液塔器的固有频率，与空塔相差很小，无法体现储液对塔器振动特性的影响，并且其计算得到的共振临界风速大于实际值，可能导致设计的误判，使得设计偏于不安全。