基于多变量时间序列模型的中牟县地下水埋深预测

孙俊志，张 娅，孙丰博，闫佰忠

1.河南省地矿局第二地质勘查院，河南 郑州 450018；2.河南省地矿局第二地质环境调查院，河南 郑州 450053；3.河北地质大学 水资源与环境学院，河北 石家庄 050031

0 引言

水资源是人类生活的先决条件，而地下水是水资源的重要组成部分，是构成生态环境的关键因素，也是社会稳定发展的保障。20世纪90年代初以后，地下水逐步成为河南省重要的供水水源，对保障河南省饮水安全、粮食安全和生态安全等具有十分重要的作用[1]。中牟县地处河南省中部偏东，紧邻河南省省会郑州市，近年来随着人口的增长和工业的发展，地下水开采量也大幅度提高[2]；地表水资源，如贾鲁河，已经变为季节性河流。地下水资源短缺已经严重制约了中牟县经济社会的可持续发展。

地下水埋深动态变化是一个繁杂的过程，是人类活动和自然因素相互影响、相互作用下的结果。地下水埋深预测模型基本类型有：系统分析方法、人工神经网络分析法、灰色系统模型、回归分析模型、相关分析模型等，这些模型在地下水埋深的预测中有一定的积极作用，但是这些模型的建模方法要求时间序列要具有平稳性和独立性，在反映地下水埋深动态的复杂性方面仍有一定的差距[3-5]。时间序列太复杂，得出的预测结果就不精准，一般用多变量自回归CAR模型代替CARMA模型，对动态系统实行统一建模分析[6]。本文讨论了影响中牟县地下水埋深的主导因素，并在此基础上依据CAR模型建立地下水埋深预测模型，为中牟县地下水资源的合理开发利用提供理论指导。

1 研究区概况

中牟县位于河南省中东部，面积1 393 km2，隶属郑州市，总人口约113.44万人，地理坐标为北纬34°26′～34°56′，东经113°46′～114°12′；中牟县西临郑州城区，东邻开封市，北部与原阳县接壤，由黄河隔开，南与新郑市、尉氏县相邻(详见图1)。中牟县属于温带大陆性季风气候，年均降雨量600.8 mm，年均蒸发量为1 500.6 mm，年平均气温14.4℃。中牟县河流众多，主要有贾鲁河、运粮河、七里河等。

中牟县地处黄淮平原，地形相对来说较为复杂，地貌多变。中部、北部受到河流影响形成了两大扇形槽状地带。中牟县南部、北部、西部地势高，东部地势偏低，土壤类型以粉砂土、亚砂土为主，境内地层上部为新生代第四纪松散沉积物，沉积岩岩性主要为黄河冲积物与洪积物[7-9]。

图1 郑州市中牟县交通位置图Fig.1 Zhengzhou Zhongmu district traffic location map

2 数据来源和研究方法

2.1 数据来源

本文的地下水埋深数据采用了中牟县水务局在境内布设的15个监测井的近13年数据资料；地下水开采量、年径流量来自郑州市2002—2014年的水资源公报；气温、降水量、蒸发量的数据来自河南省气象档案馆资料。

2.2 研究方法

2.2.1 Spearman相关分析法

Spearman相关分析是权衡变量之间依附性的非参数指标，主要利用单调方程来衡量因素间的相关性，即秩次的大小作线性相关分析，经常用希腊字母ρ来表示；相较于Pearson相关分析，Spearman相关分析不需要x、y服从双变量正态分布，所以适用范围要比Pearson相关分析更广[10]。

一个容量为n的样本数据，n个原始数据转化为等级数据，相关系数ρ为：

(1)

而相关系数r范围为-1～1之间；r>0，为正相关，r<0，为负相关，本文利用SPSS25软件进行Spearman相关分析。

2.2.2 多变量时间序列模型的构建

假定用m个变量的时间序列组建n阶的CAR模型，形式为：

yt=atyt-1+a2yt-2…anyt-n+b10x1,t+b10x11,t-1+b12x1,t-2…b1nx1,t-n+b20x2,t+b21x2,t-1…b22x2,t-2+…b2nx2,t-n+…+bm0xm,t+bm1xm,t-1+bm2xm,t-2…bmnxm,t-n+εt

(2)

式中，{an}、{bmn}为系数，其中m，n为正整数，yt，xm,t-n为时间序列变量，t为时间序列，t>1[11-13]。再进行递推最小二乘法估计参数：

(1)令

(3)

CAR模型一般形式为：

(4)

(5)

α为遗忘因子，取值为0.9～1.0之间。

利用N组观察值的CAR(n)模型计算残差平方和S(n):

(6)

(2)模型最高阶n的判定

CAR模型的判定是根据已知的N个样本(xj,t，yt，t=1，2，…，N；j=1，2，…，m)，从低阶到高阶递增式拟合CAR模型。对相邻两个CAR模型阶次增长是否合适采用F值检验法进行判断。在分析时取置信度α=0.05，得出相应临界值Fα，当相邻的FFα时，CAR(n)模型不合适。

(3)模型真实阶和时滞判别

按以上步骤得到合适的CAR(n)，但仍旧有一些不足。某些参数的系数可能为0，因此需要检验，首先剔除接近0的参数，再次运用递推最小二乘法建立含较少参数的新模型。若检验结果显著，那原来的CAR(n)模型为真；反之，以新建立的模型为真[14-15]。

3 地下水埋深影响因素分析

根据中牟县2002—2014年15个监测井的地下水埋深数据绘制出变幅图(见图2)。由图可知，中牟县地下水埋深年际变化较大，在2002—2014年13年时间里累计下降了2.79 m。地下水埋深下降主要分为3个阶段：2002—2006年间，地下水埋深从5.38 m升高至3.76 m，2004—2005年稳定在3.7 m左右，随后2006年又回落至5.39 m；2008—2010年，地下水埋深呈现稳定下降状态，从2007年4.28 m下降到2010年4.61 m，降幅为0.33 m；2011—2014年，地下水埋深大幅下降，从2011年4.47 m下降至2014年8.17 m，4年共下降3.7 m，下降速率为0.925 m/a。

运用Arcgis10.5将15个观测井2002、2005、2008、2011和2014年地下水埋深数据进行IDW反距离权重插值分析(详见图3)。由图可知，在这13年间中牟县地下水埋深最大区域为中部的城关镇与姚家乡和韩寺镇的北部，由2002年的10.64 m下降到2014年的14.28 m，降幅达到了3.64 m；东北区域的雁鸣湖镇和官渡镇的韩庄村是地下水埋深最浅的区域，但地下水水位仍呈下降趋势，雁鸣湖镇的水位由2002年的0.83 m下降到2014年的6.41 m，降幅达到了5.58 m，韩庄村的水位由2002年的2.46 m下降到2014年的3.87 m，降幅达到了1.41 m；中牟县南部乡镇的地下水水位经历了上升再下降的阶段，2002年平均水位5 m，2008年地下水位上升到最高，为4 m，随着开采程度的增加，到2014年地下水位持续下降，最南端的三官庙乡高低水位差值最大达到了8.59 m。

图2 中牟县2002—2014年地下水埋深变幅图Fig.2 Variation map of groundwater depth in Zhongmu district from 2002 to 2014

图3 中牟县2002、2005、2008、2011和2014年地下水埋深图Fig.3 Groundwater depth maps of Zhongmu district in 2002, 2005, 2008, 2011 and 2014

4 地下水埋深主要影响因素的提取

为了挑选出对中牟县地下水埋深变化影响程度较大的因子，利用Spearman相关分析法进行选取。选取2002—2014年中牟县地下水开采量X1、年降水量X2、年蒸发量X3、气温X4和年径流量X5作为输入因子，地下水埋深为y，利用SPSS25来进行双变量Spearman相关分析(详见表1)[16]。

表1 地下水埋深Spearman相关分析结果表Table 1 Spearman correlation analysis of groundwater depth

地下水开采量X1对地下水埋深的影响最大，为0.618；其次是年降水量X2、年蒸发量X3与地下水埋深的相关性较好，分别为-0.606和0.602；气温X4与年径流量X5显著性并不强，分别为0.412和0.484。

5 CAR模型的建立与应用

5.1 确定参数和建立模型

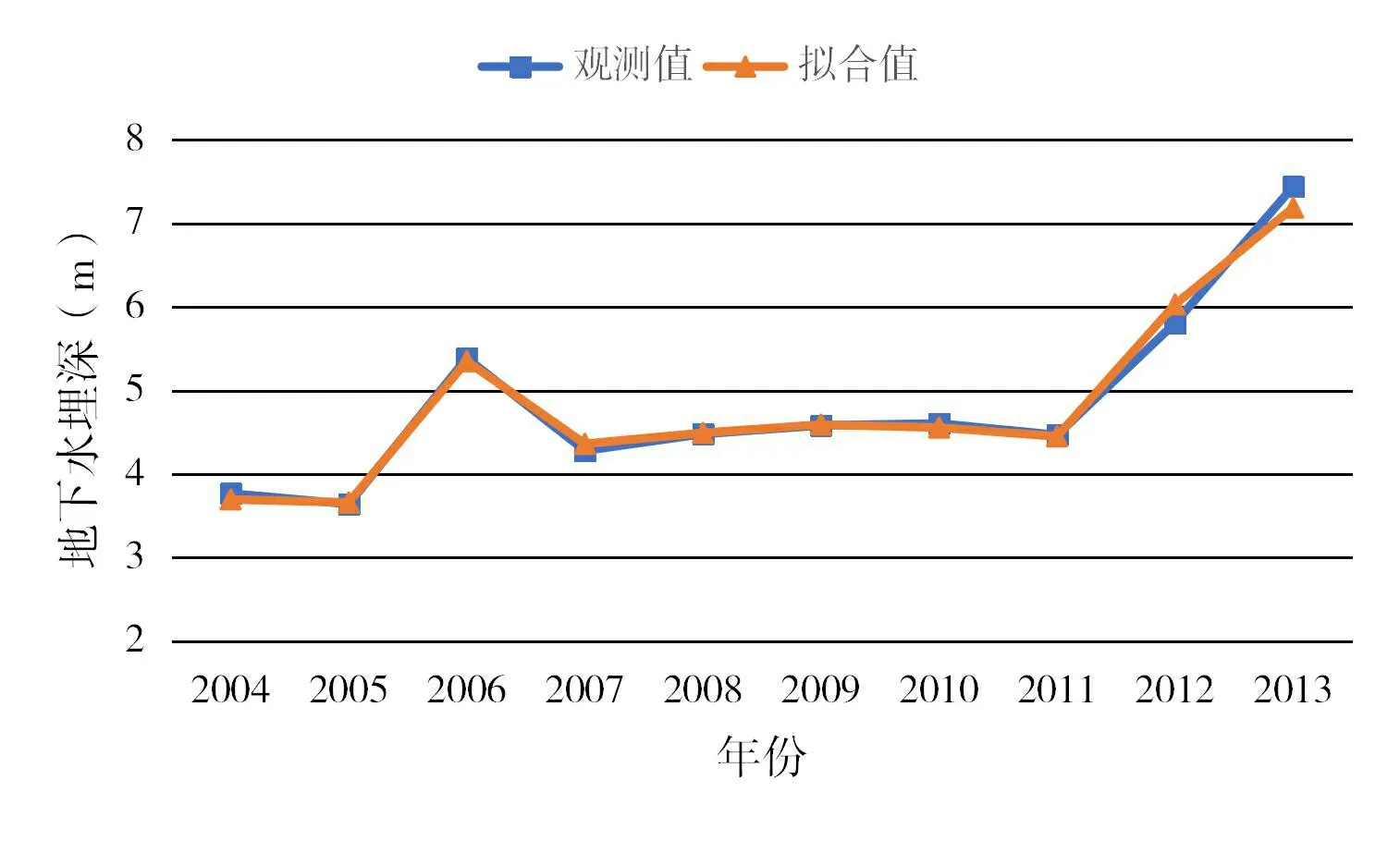
通过Spearman相关分析法我们可以得出下水开采量、年降水量、年蒸发量对中牟县地下水埋深有较大影响。把这三个变量作为输入变量，中牟县地下水埋深为输出变量，建立多变量时间序列CAR模型。其中，F=3.025，模型定阶的F检验值为0.767；残差平方和S=0.001 4，选定阶次并剔除不显著项后，模型残差平方和S=0.001 9，是否剔除不显著因子的F值为0.38，F(α=0.05)=19，F

Y(t)=9.38×10-1Y(t-1)+5.02×10-1Y(t-2)-1.99X(1,t-1)-1.02X(1,t-2)+6.6×10-3X(2,t)-7.8×10-3X(2,t-1)+1.6×10-2X(2,t-2)-9.7×10-3X(3,t-1)+7.4×10-3X(3,t-2)

(9)

式中：t为时间序列编号，t>1。

5.2 检验模型

采用2004—2013年共10年的中牟县地下水埋深数据观测值和以上模型的拟合值制作成图表(见图4，表2)来检验模型的预测结果。从模拟曲线和比较表中我们可以看出，观测值与拟合值吻合较好，相对误差较小，控制在正负3.5%以内。说明所构建的模型可以较好地反映中牟县地下水埋深的变化趋势，并且具有良好的预测性。

图4 地下水埋深观测值与拟合值对比曲线Fig.4 Comparison curve of observed and fitted values of groundwater depth

表2 地下水埋深观测值、拟合值和相对误差表Table 2 Table of observation, fitting and relative error of groundwater depth

表3 中牟县地下水埋深预测方案Table 3 Prediction scheme of groundwater depth in Zhongmu district

5.3 CAR模型的实际预测

依据中牟县的社会发展、气象条件的变化、地下水资源短缺等条件，将2014年作为基准年，根据地下水开采量、年降水量、年蒸发量等资料，拟定3种地下水开采方案，用CAR模型计算3种方案下中牟县地下水埋深变化情况(详见表3)。

由表3可知，地下水开采量减少10%，年降水量减少5%，年蒸发量增加5%时，地下水埋深将达到7.77 m；地下水开采量减少15%，年降水量减少10%，年蒸发量增加10%时，地下水埋深将达到7.63 m；地下水开采量减少20%，年降水量减少15%，年蒸发量增加15%时，地下水埋深将达到7.48 m；所以根据中牟县气候变化具体情形，减少地下水开采量，可以使得地下水埋深减小，对当地的地下水资源具有积极意义。

6 结论

(1)依据Spearman相关分析法，得出中牟县地下水开采量对地下水埋深影响程度最大，为0.618，其次为年降雨量和年蒸发量，分别为-0.606和0.602；科学合理控制地下水开采量对中牟县的农业发展，经济发展以及生态环境具有重要意义。

(2)观测值与建立的预测模型相比，相对误差均在3.5%以内，这说明CAR模型的预测精度高、效果好。预测模型表明，地下水开采量减少10%，年降水量减少5%，年蒸发量增加5%时，地下水埋深将达到7.77 m；地下水开采量减少15%，年降水量减少10%，年蒸发量增加10%时，地下水埋深将达到7.63 m；地下水开采量减少20%，年降水量减少15%，年蒸发量增加15%时，地下水埋深将达到7.48 m。

论文中建立的地下水埋深的多变量时间序列模型具有一定的局限性，地下水埋深是一个复杂的过程，论文选取的参数仅仅是影响因素较大的，不能代表所有的参数，因此模型的预测效果和精度还有一定的提升空间。进一步讨论地下水埋深的影响因素，提高模型预测效果和精度是此类研究的发展方向。