基于蚁群优化算法的应急避难场所选址模型研究

杜浩国，林旭川，张方浩，汤筱麒，卢永坤，曹彦波

(1.云南省地震局，云南 昆明 650224； 2.中国地震局工程力学研究所，黑龙江 哈尔滨 150080)

应急避难场所是地震发生后受灾居民紧急疏散的重要场所[1-2]，对城市安全和可持续发展有着很重要的作用，国内外越来越多的城市相继开展了应急避难场所的规划和建设工作。现有城市避难场所可分为公园、绿地、停车场、广场、学校操场[3]等，这些场所在规划和建设中没有考虑避难功能，数量分布不合理且不足以满足避难需求，因此研究应急避难场所快速有效的选址方法[4-5]，具有较强的实际意义和研究价值。

国内外众多学者针对应急避难场所选址问题上有过很多的研究，可大致分为传统的选址方法、基于ArcGIS技术的选址方法、基于智能优化算法的选址方法。首先是传统的选址方法，如黄典剑从应急避难场所的规划设计、内部硬件设施、外部软件环境3个方面出发，选定18个评价指标，构造了突发事件应急避难所应急能力影响因素的层次结构，建立了综合评价模型[6]；陈明利基于系统管理视角从工作人员素质、设备设施配置、支撑结构功能、应急响应能力4个方面建立包含19个特定指标的城市体育馆应急避难服务能力评价体系[7]；王东明等[8]在总结多次地震灾区经验教训和国内外部分城市应急避难场所建设经验的基础上，对应急避难场所的功能设计及运营管理提出了建议；这些传统的选址方法能从宏观和主观的层面对应急避难场所进行选址。在基于ArcGIS技术的选址方法，朱佩娟等[9]运用ArcGIS与元胞自动机相结合的方法，构建2015年人口空间分布模型和交通流量综合预测系统模型，从城市均衡发展以及最大限度发挥城市公共绿地防灾避难功能的角度，对公共绿地合理的服务半径和空间布局进行研究；Kar和Hodgson[10]采用ArcGIS栅格数据模型，综合洪灾影响区、危险源，与快速路、疏散通道和医疗卫生机构临近度，以及人口分布状况等因素，评价了南弗罗里达避难场所合理性；Yu[11]采用遥感影像提取的土地利用类型与人口普查数据，根据人口行为特征，分别评价白天与夜间避难场所满意度；将ArcGIS技术融入到应急避难场所选址方法中，有效提高了应急避难场所选址的精确度和可视化程度。最后是基于智能优化算法的选址方法，近年智能优化算法被广泛关注，因为它们能处理大量的数据，并且能大大提高空间优化搜索能力，能在合理的时间内找到近似最优解，所以越来越多地被应用到选址模型中，如张富[12]设计了求解避难场所个数、疏散时间、人员分配的平衡性、在疏散过程中不同线路的速度构建了数学模型问题的一个启发式算法；陈志芬等[13]分析了应急避难场所层次选址的决定因素和基本目标，建立了8个包含临时、短期、中长期三级层次的应急避难场所选址模型，模型通过Lingo优化软件求解确定出各层次避难场所的数量和具体位置，从而确定避难者在避难过程中的移动方向以及移向不同方向的人数；袁昀等[14]构建了多智能体进化算法，并将准备度指标引入应急设施选址问题中，综合考虑需求就量、离设施距离和距离决定的权重，对每个社区的应急服务覆盖程度进行量化，从而保证将应急避难场所设置在合理的位置；李强等[15]采用事故风险影响因子与疏散方向因素的道路容量需求(BLD)等方法来表示道路网络中的各节点疏散风险；ZHANG Nan等[16]选择了影响行人疏散道路风险的8个影响因子，包括道路节点度、宽度、安全性、电阻系数以及建筑的威胁、行人逆流、违章停车和交通流，基于复杂网络理论、电路理论和道路实际情况，建立了道路风险综合评价函数，分析了不同情况下行人疏散道路风险，绘制了风险分布图，直观地显示了风险水平。

以上的研究都取得了一定的成果，特别是智能优化算法的引入，对应急避难场所快速有效选址问题具有重要意义[17]，本文在传统选址的基础上，归纳总结了8个应急避难场所重要选址指标，并采用智能蚁群优化算法、遥感技术与ArcGIS相结合的方式构建了基于蚁群优化算法的应急避难场所选址模型，该模型能够有效提高城市应急避难场所选址的合理性和科学性。

1 研究方法及技术路线

1.1 技术路线

图1为基于蚁群优化算法的应急避难场所选址模型流程图，其中第一步数据收集，采用无人机遥感技术获取研究区遥感影像、DSM(Digital Surface Model)数字地表模型[18]；第二步数据处理，本文在阅读大量相关文献的基础上，归纳总结了8个应急避难场所重要选址指标，并以云南红河县城作为研究区，将不同选址指标加入到应急避难场所选址模型中；第四步蚁群算法与ArcGIS结合，采用智能蚁群优化算法、遥感技术与ArcGIS相结合的方式构建基于蚁群优化算法的应急避难场所选址模型；第五步对比分析，采用穷举法与实地调研方式对模型选址结果进行验证。

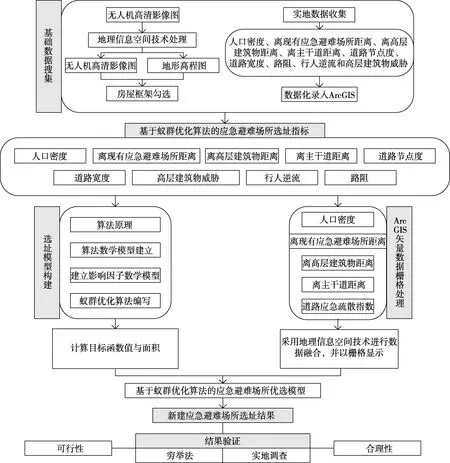
图1 基于蚁群优化算法的应急避难场所选址模型流程图Fig.1 The flow chart of studying on emergency shelter location model based on ant colony optimization algorithm

1.2 蚁群优化算法

1.2.1 蚁群算法数学模型

蚁群优化算法是模拟蚂蚁觅食的原理，设计出的一种群集智能算法。蚂蚁起初选择路径是随机性的[19-20]，可用数学模型公式(1)表示，即在t时刻，蚂蚁k从地点i去往地点j的移动概率[21-22]：

.

(1)

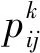
(2)

式中：dij表示地点i和地点j之间的距离；β表示蚂蚁在搜寻途中启发信息对蚂蚁下一步移动方向的影响程度(β≥0)；Tbs蚂蚁所能搜寻的所有地方。

对于不同信息素更新原则，M.Dorigo等曾经给出了3种类型的蚂蚁模型，分别为蚁量模型、蚁密模型和蚁周模型[23]，由于蚁周模型相比于2种模型具有较好的信息更新策略，因此本文选用蚁周模型进行算法信息更新，如公式(3)所示：

(3)

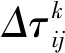
1.2.2 算法目标函数

蚁群算法目标函数综合了影响选址的各个指标，用于删选出应急避难场所选址最优解。每一只蚂蚁代表着相应的目标函数值，通过对比蚂蚁搜寻得到的目标函数值大小来进行应急避难场所的选址。由于城市用地的紧张，避难场所修建的面积与成本关系成正相关，因此本文通过对避难场所修建面积或费用进行设定，采用蚁群优化算法，求解出最优选址方案，目标函数见下式：

(4)

式中：Dstreet(i,j)表示第(i,j)栅格离主干道距离，η1和η2表示各选址指标影响系数；ρ(i,j)表示第(i,j)栅格的人口数量；a表示纵向栅格数，b表示横向栅格数；Dmin(i,j)表示第(i,j)栅格到离指定栅格之间的距离；S表示栅格所在实际面积；M为求解的栅格个数，t表示相关系数。

1.3 应急避难场所选址指标

中国地震局震灾应急救援司关于《应急避难场所的规划原则》中强调：(1)应急避难场所规划要与城市现状相结合，应结合城市现有的人口密度、建(构)筑物情况，建设用地情况，安全性等因素综合考虑和安排避难场所；(2)避难场所要有快速畅通的道路与之相联通，避难场所和道路的设计与安排应尽量利用已有的基础和条件，节约用地；(3)应急避难场所要有一定的面积，有助于设置应急设施如帐篷、简易厕所；(4)应急避难场所应远离高大建筑物。本文对以上选址标准进行总结分析，选取了8个易于获取数据的指标，分别为人口密度、离现有应急避难场所距离、离高层建筑物距离、离主干道距离、道路节点度、道路宽度、路阻和行人逆流。

1.3.1 人口密度

应急避难场所应建立在人口密集且人流量大的区域，有助于紧急状态下大面人员的疏散与安置。因此人口分布情况是规划避难场所时需要参考的重要指标，本文根据Yu J等[11]的人口估算公式，计算云南红河县城区每栋建筑物的人口数量，如公式(5)、(6)所示。

(5)

(6)

式中ρH(n)为第n个建筑物的夜晚人口；ρnighttime为在夜间总的居住人口；ρC(k)为第k个居委会的常住人口总数；SH(i)为第i个建筑物的占地面积；FH(i)为第i个建筑物的楼层数；M(k)为第k个居委会的建筑物数量；K为红河县城区内居委会的总数；N为红河县城区内建筑物的总数。

1.3.2 离现有避难场所距离

新建应急避难场所应与现有避难场所保持合理的距离。随着城市的快速发展，土地资源紧张，为了提高城市土地资源的有效利用率，新建的应急避难场所应与现有的应急避难场所保持一定的距离，分别服务不同的地域，避免土地资源的浪费[22-23]。

1.3.3 离高层建筑物距离

应急避难场所应与高层建筑物保持一定的距离，如果应急避难场所建立在高层建筑物较近的范围内，当发生地震时，高层建筑物的倒塌很可能毁坏应急避难场所，造成更多的人员伤亡。因此应急避难场所的建立应远离高层建筑物一定距离。

1.4 道路应急疏散指数

本文根据Zhang Nan等[16]的研究成果，将道路应急疏散指数作为一项重要选址指标。道路应急疏散指数是指在紧急状下疏散人群遇到的交通阻碍情况，包括行人逆流、道路宽度、路阻、道路节点度、高层建筑物威胁。

1.4.1 道路宽度

道路宽度决定了疏散人群的通过量，当发生地震时，道路越宽第一时间疏散的人数就越多。本文道路宽度为疏散道路面积除以疏散道路长度，如公式7所示：

RW=RS/RL.

(7)

式中：RW表示疏散道路平均宽度；RS表示疏散道路面积；RL表示疏散道路长度。

1.4.2 道路节点度

道路节点度是指该道路可以联通的道路节点数，道路节点度反映了道路可以访问的路口数量。如图2所示，路段AB两端分别为A点和B点，A点为T字型路口共有3个路段，所以规定A端的节点度为3，相应的B端的节点度为2，因此路段AB的总节点度为5。同理BC路段节点度为4，CD路段节点度为6。道路E端为封闭道路其节点度为0，因此路段DE的总节点度为4。紧急疏散过程中，道路节点度越大，疏散的安全性就越大，疏散人群就会集中于此路段。

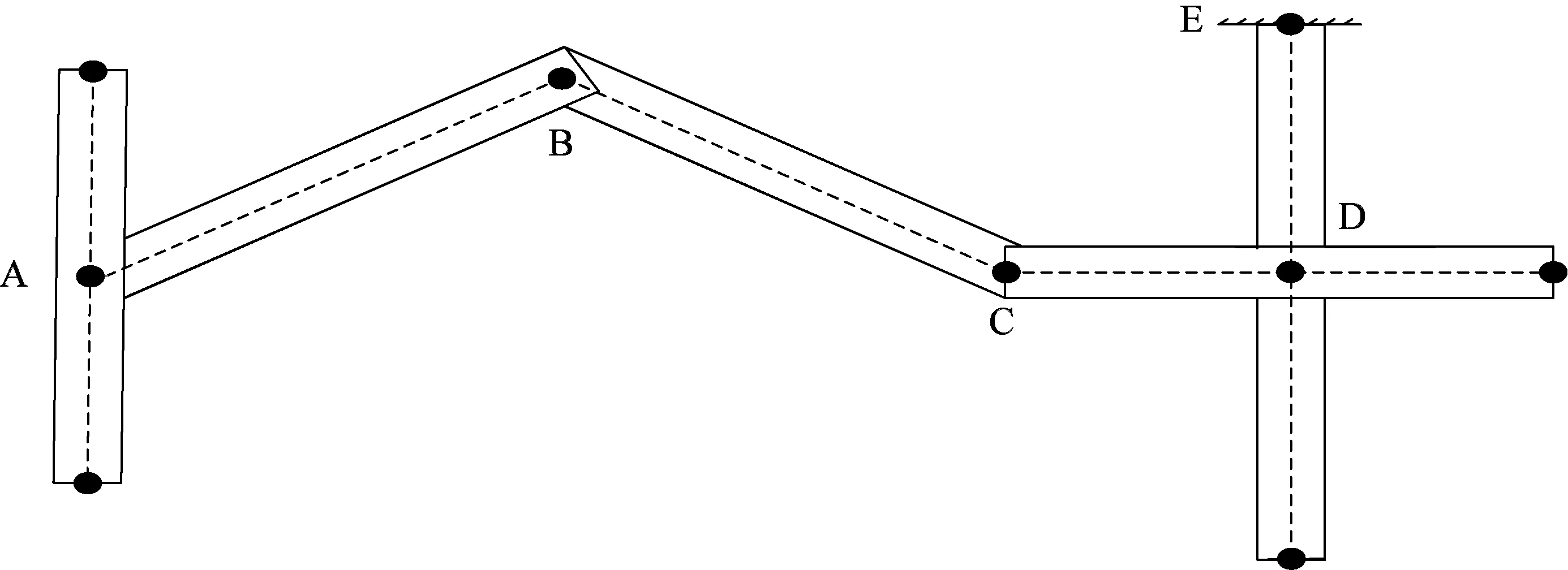
图2 道路节点度示意图Fig.2 The diagram of road degree diagram

1.4.3 道路电阻系数

本文将路网作为计算道路电阻的电子电路，用电路理论中的基尔夫定律计算道路电阻系数。道路的节点在电子电路中被视为节点，而道路被视为节点之间的电阻。此外，行人流被认定是电子电流，用道路电阻系数来反映道路疏散困难程度，路阻系数公式如下：

(8)

式中RL为道路长度，RW为道路宽度。

1.4.4 高层建筑物的威胁

当发生地震时，会造成高层建筑倒塌，对道路通行造成阻碍，即疏散道路越靠近高层建筑物，应急疏散风险越大，因此疏散道路应远离高层建筑物一定距离。高层建筑物对道路的威胁公式如下：

(9)

式中：N为疏散道路两边高楼数量，H(i,j)为建筑物(i,j)高度，D(i,j)为建筑物(i,j)离道路的距离。

1.4.5 行人逆流

在紧急疏散过程中，大部分疏散人群会向应急避难场所移动，但其中也会出现逆流的人群或车辆阻碍疏散，如救援人员和车辆的进入或返回寻早失散家人等情况。本文参考Zhang Nan等[16]的研究成果，行人逆流计算方法见下式：

(10)

式中Rpc为行人逆流影响指标，RW为疏散道路宽度。

1.4.6 道路应急疏散指数数学模型

本文综合5个选址指标路宽、道路节点度、路阻、高层建筑物的威胁和行人逆流，确定道路应急疏散指数数学模型，如公式(11)所示。

(11)

其中α，β是比例系数，参考Zhang Nan等[16]的研究成果，本文研究中α=0.5，β=2。

1.5 目标函数的确定

由于选址时需要考虑人群疏散的时效性，因此本文选取了8个选址指标人口密度、离现有应急避难场所距离、离高层建筑物距离、离主干道距离、道路节点度、道路宽度、路阻和行人逆流，并确定了目标函数，如公式(12)所示。

(12)

其中，a表示纵向栅格数，b表示横向栅格数；ρ(i,j)表示第(i,j)栅格的人口数量；Vr(i,j)为栅格i到栅格j路径的道路应急疏散指数；Dstreet(j)为栅格j到主干道的距离；Dhigh(j)为栅格j到高层建筑的距离；Dshelter(j)为栅格j离现有应急避难场所距离。目标函数值越小，应急避难场所选址条件越好。

2 数据来源与处理

2.1 研究区概况

红河县位于云南省南部，红河上游南岸，隶属红河哈尼族彝族自治州，是云南省地质灾害高易发区。境内河谷狭窄，地势大致中部高，南北低，山地面积大，主体位于红河流域与勐龙河流域之间的迤萨梁子顶端，是云南省典型的高原山地县城之一[24-25]。县城城区地质构造复杂，地处横断山脉纵谷区的南缘和哀牢山余脉地区，新构造运动强烈，峰峦起伏，沟壑纵横，冲沟发育，岸坡陡峻，软弱岩体发育[26-27]，人类过程活动强烈，地质灾害不断孕育。县城人口密度高，房屋建筑结构类型较多，抗震性能有待加强。红河县城区现有应急避难场所共计14个，但是由于城区人口密集程度高，现有应急避难场所还远远不能满足突发灾害时居民的避难需求，因此城区新建应急避难场所迫在眉睫，新建应急避难场所合理选址尤为重要。图3为通过无人机获取的遥感影像与基于ArcGIS地形矢量图。

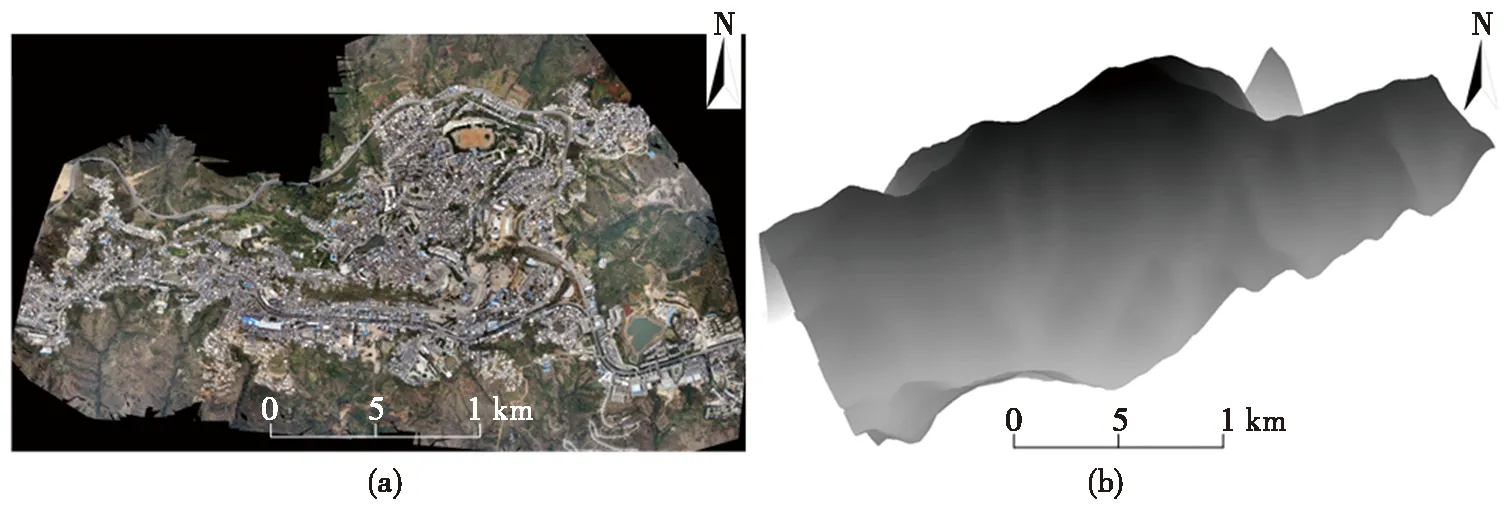
图3 红河县城无人机遥感影像和地形矢量图Fig.3 The UAV remote sensing image and terrain vector image of Honghe County

2.2 土地与建筑物数据矢量化

通过无人机遥感影像对红河县城区土地利用和建筑物进行矢量化，其中土地用途分类参考《城市用地分类与规划建设用地标准》和FEMA(美国联邦应急管理署)在HAZUS模型中提出的土地分类标准，提出表1的土地分类。图4(a)为红河县城区土地利用矢量图，图4(b)为红河县城区建筑物矢量图。

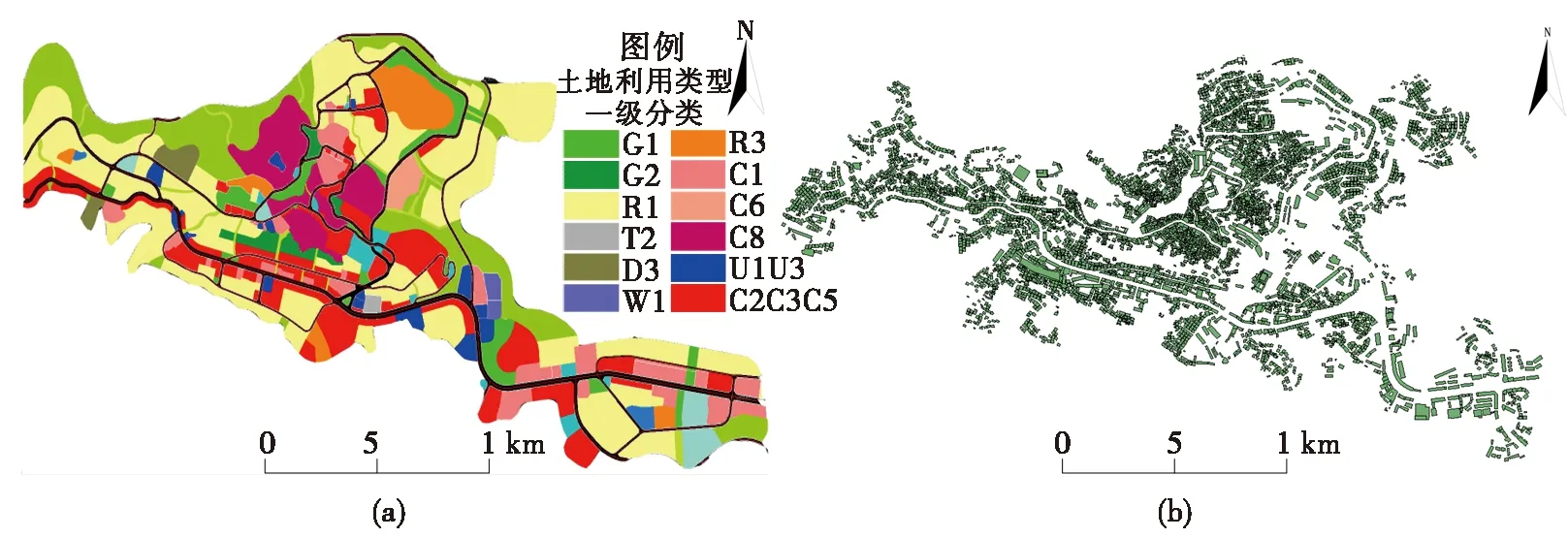
图4 红河县城区土地利用矢量图(a)和红河县城区建筑物矢量图(b)Fig.4 Vector map of urban land(a) and use building vector map in Honghe County(b)

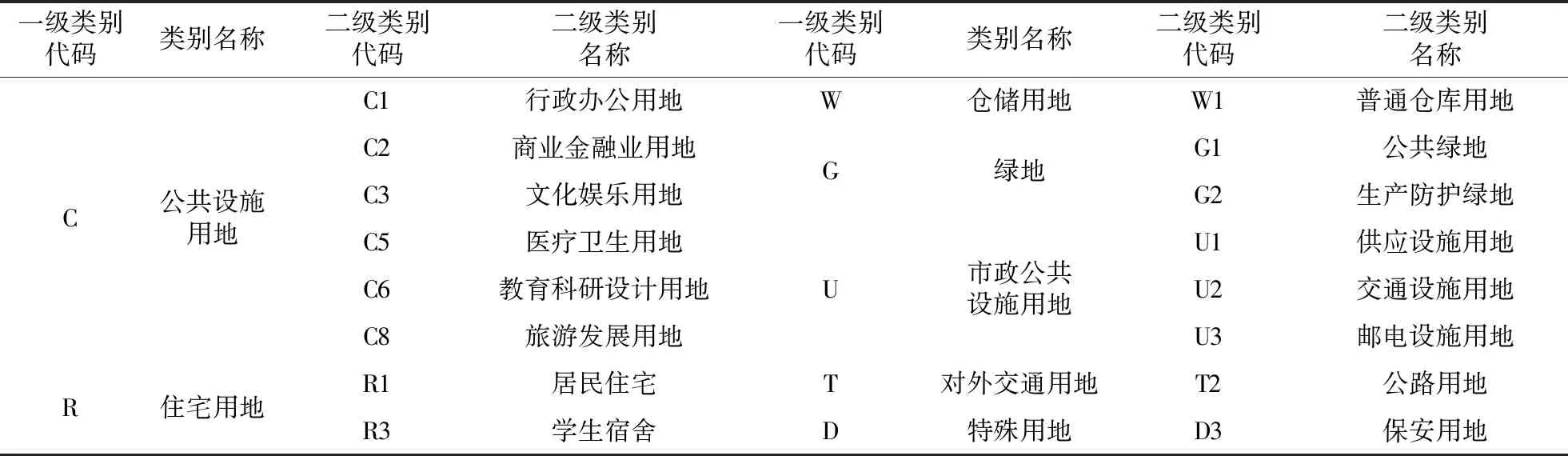
表1 城市用地分类代码表(部分)Table 1 The classification code table of urban land (Part)

2.3 人口密度

根据Yu J等[11]的人口估算公式(5)、(6)，计算红河县城区每栋建筑物的人口数量，得到图5(a)红河县城区建筑物人口分布图。本文选址模型是以栅格数据为基础，栅格数据的获取方式是通过ArcGIS将矢量数据转为固定栅格数据，如图5(b)为红河县城区建筑物人口分布栅格图，其中矢量图转换栅格图设置像元大小为40。

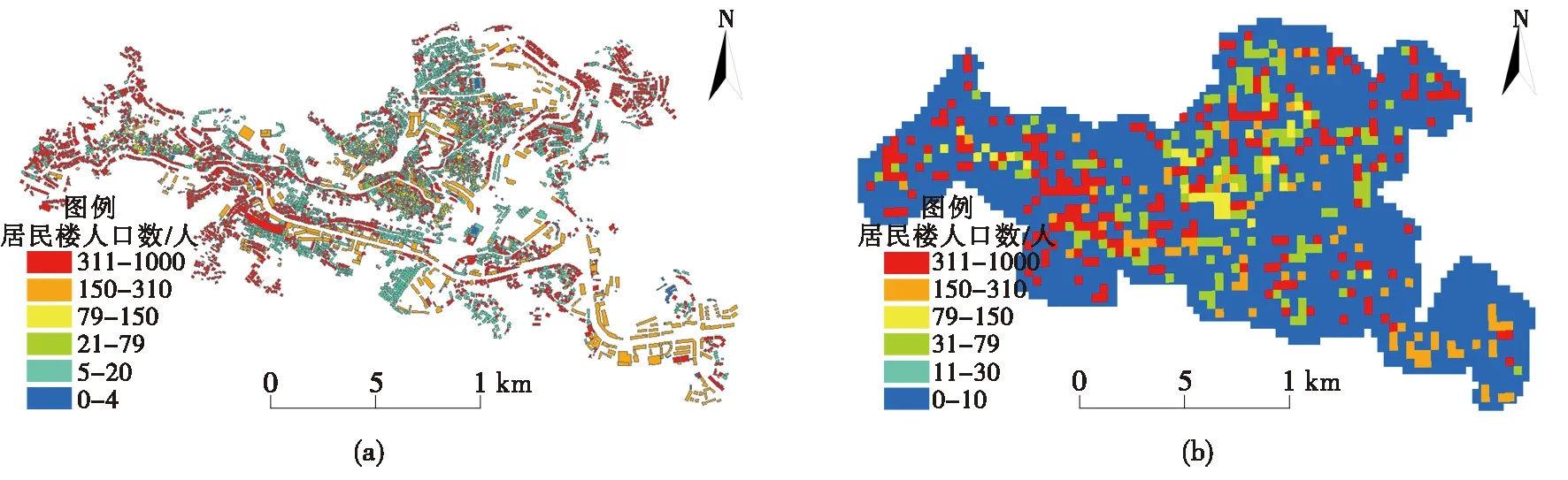
图5 红河县城区建筑物人口分布图(a)、人口分布栅格图(b)Fig.5 The building population distribution map(a) and Population distribution grid(b) in Honghe County

2.4 离现有应急避难场所距离

图6(a)为红河县城区现有应急避难场所分布图，此次选址模型将红河县城区中面积大于1 000 m2的公园、绿地、广场提取出来，作为待建应急避难场所。新建应急避难场所离现有应急避难场所距离计算方法：首先将红河县城区数据生成49×84的网格，即得到城区空间网格图；然后将网格图与现有应急避难场所分布图进行位置匹配，分别计算每个网格与现有应急避难场所的距离；最后将距离网格通过ArcGIS转化为栅格数，转化像元参数大小为40，得到图6(b)离现有应急避难场所距离的分级图。

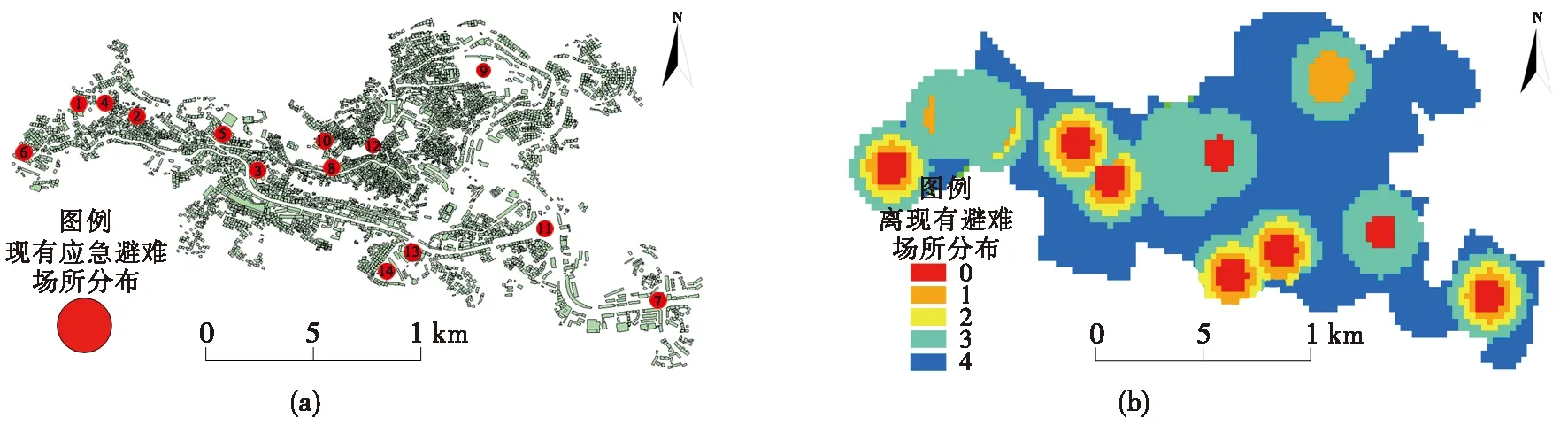
图6 红河县城区现有应急避难场所分布图(a)、离现有应急避难场所距离分级图(b)Fig.6 The map of existing emergency shelters(a) and the grading map of distance from existing emergency shelter in Honghe County(b)

2.5 离高层建筑物距离

应急避难场所的选址应离高层建筑物一定距离，即高层建筑物倒塌影响小的区域。本文删选出建筑物高度大于24 m的高层建筑物，如图7(a)为高度大于24 m建筑物分布图，并且将高层建筑物高度的一半作为倒塌影响大小的边界，将计算好的边界矢量数据转为栅格数据，转化时像元参数大小为40，得到如图7(b)所示的受高层建筑物影响的区域分布图。

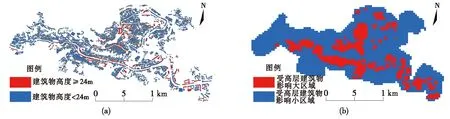
图7 高层建筑物分布图(a)、受高层建筑物影响的区域分布图(b)Fig.7 The distribution map of tall buildings(a) and the map of an area affected by tall buildings in Honghe County(b)

2.6 离主干道距离

新建应急避难场所离主干道距离计算方法：同离应急避难场所距离计算方法相同，首先将红河县城区数据生成49*84的网格，即得到城区道路空间网格图，如图8(a)所示；然后将网格图与城区主干道分布图进行空间位置连接，分别计算每个网格离主干道距离；最后将距离网格通过ArcGIS转化为栅格，转化像元参数大小为40，得到图8(b)离主干道距离的分级图。

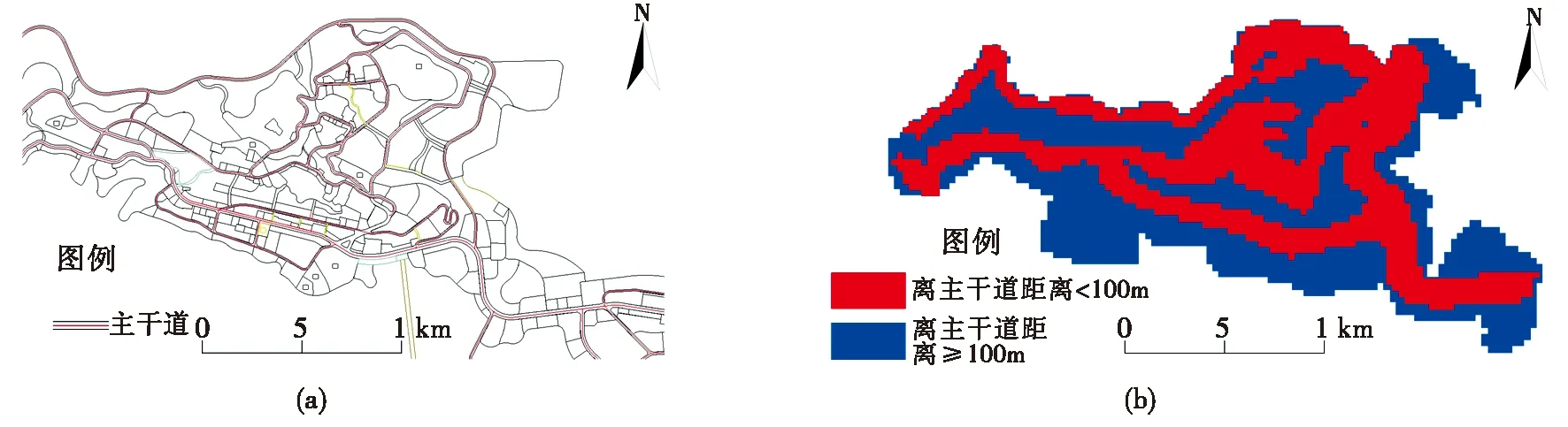
图8 红河县城区道路空间网格图(a)、离主干道距离的分级图(b)Fig.8 The road space grid(a) and the grading plan of the distance from the main road(b) in Honghe County

2.7 道路应急疏散指数

本文分别计算得到5个影响因素道路宽度、电阻系数、道路节点度、行人逆流和高层建筑物的威胁相对应的数据，并采用公式11计算得到每个路段的道路应急疏散指数，如图9所示道路应急疏散指数分级图。

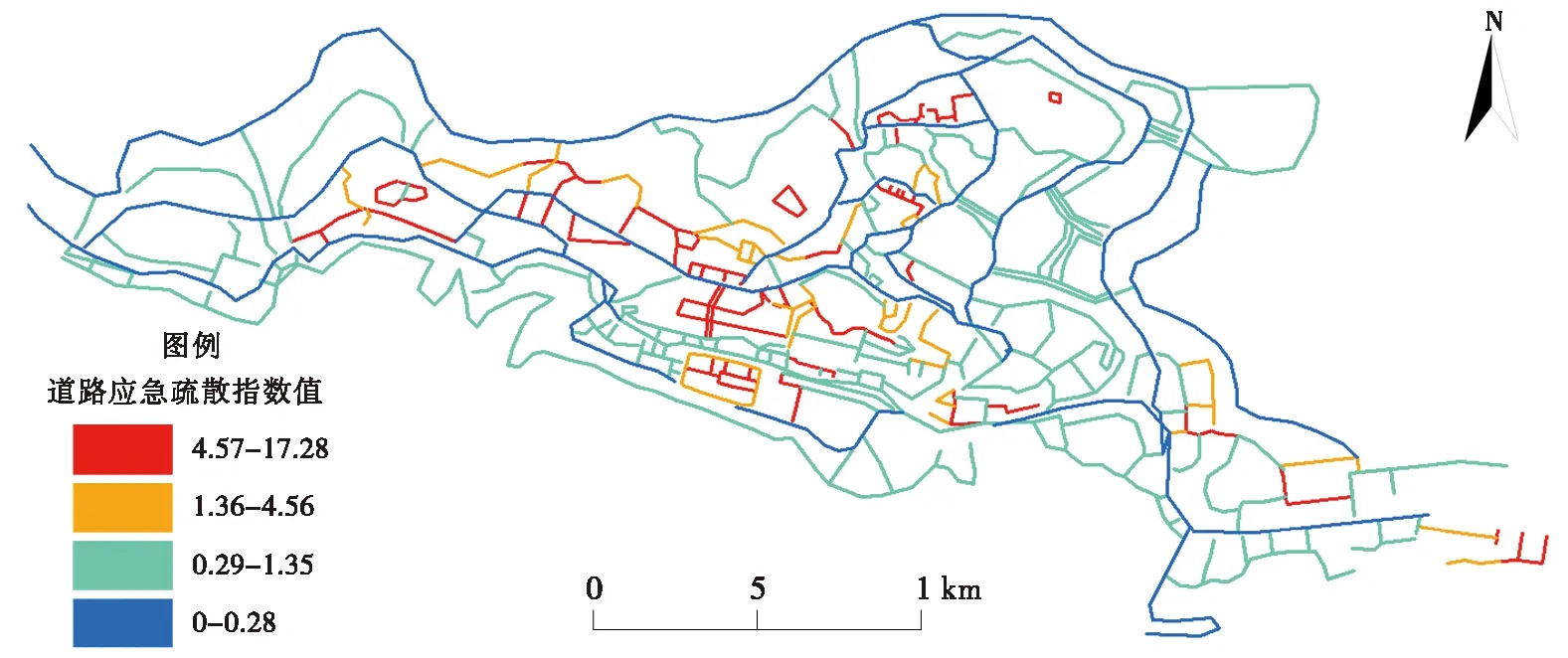
图9 道路应急疏散指数分级图Fig.9 The grading plan of road emergency evacuation index in Honghe County

2.8 蚁群算法参数设置

选址模型每组重复10次，取每组平均值进行比较，选址目标函数F越大说明蚂蚁经过数量越多，即为选址最优。计算中蚂蚁数量和重复迭代次数越多，选址结果越精确，但计算时间越长，因此合理的参数设置，使模型在可控的时间内就能得到精确的选址结果，本文参考了刘闻等[28]，吴鹏等[29]人研究成果，对模型参数进行设置：选址数量为2，蚂蚁数量为50，挥发因子为0.01，信息素初始值为40，信息素启发因子为1，期望启发因子为0.6，迭代最大重复次数为30。

3 结果

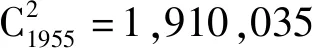
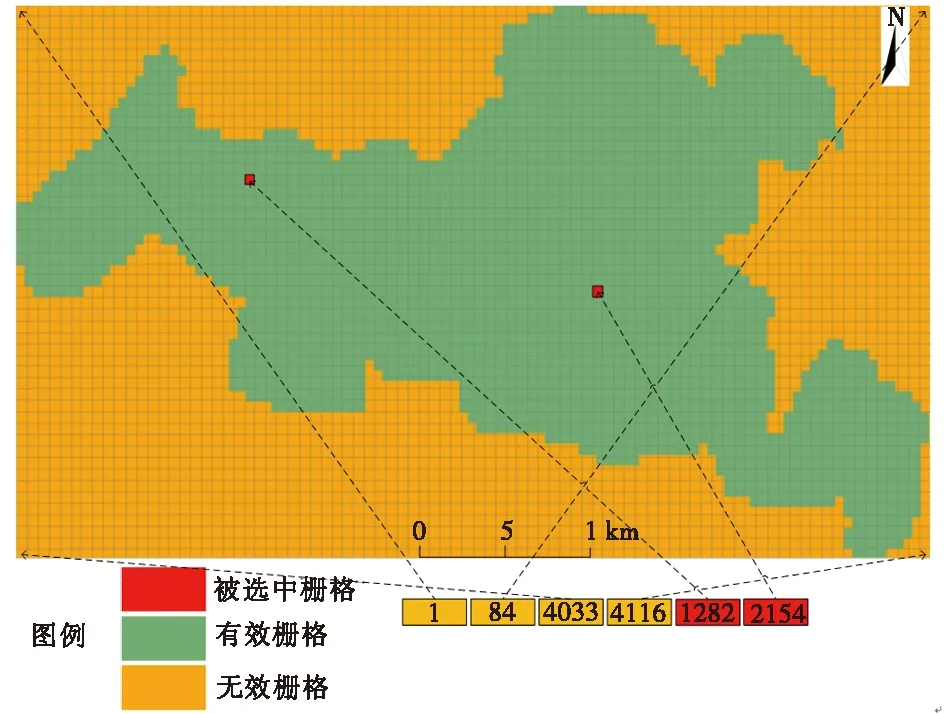
图10 基于蚁群优化算法的应急避难场所选址结果分布图Fig.10 The distribution map of studying on emergency shelter location model based on ant colony optimization algorithm

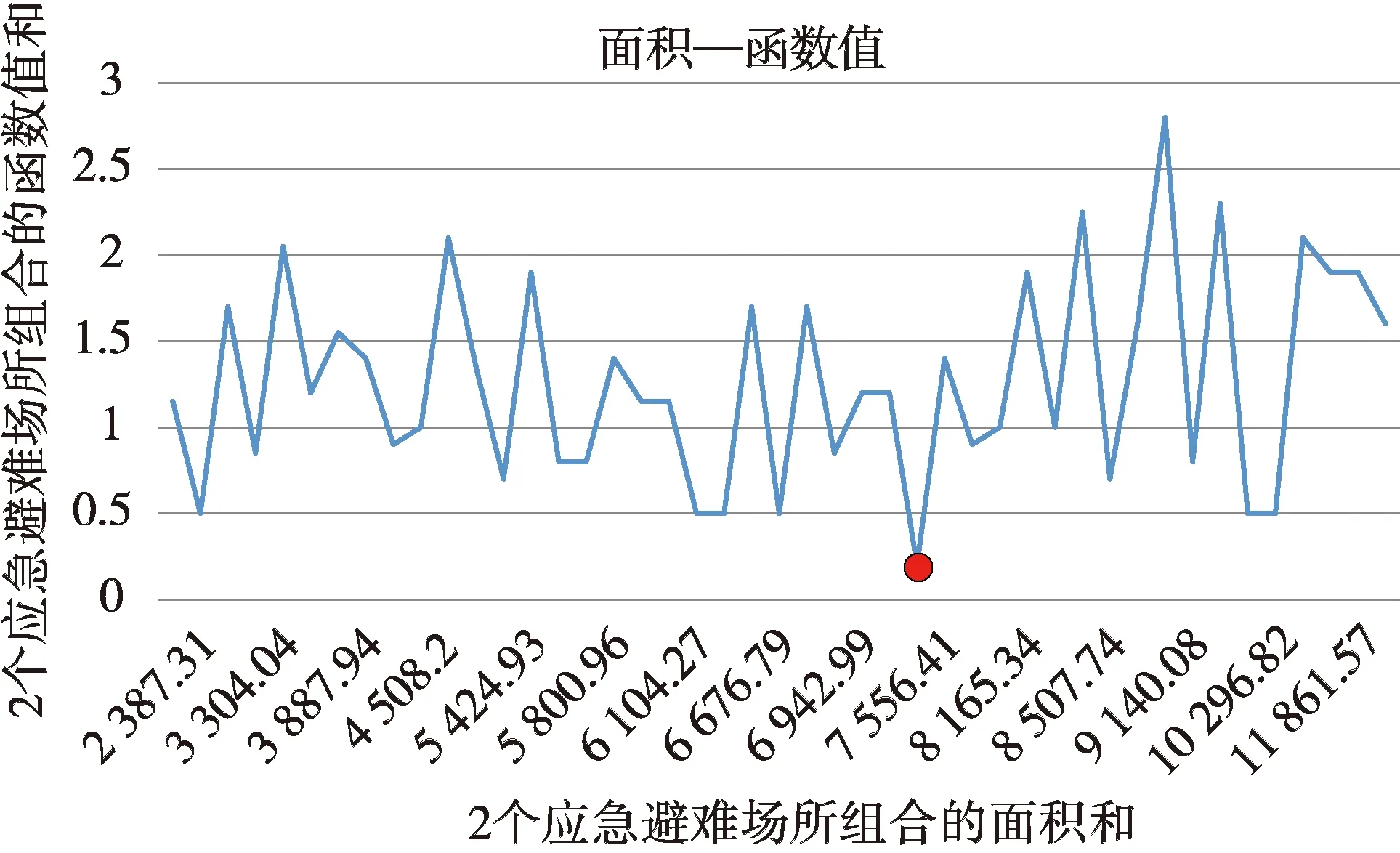
图11 45种组合方案面积与函数值对应关系Fig.11 The area of 45 combined schemes corresponds to the function value

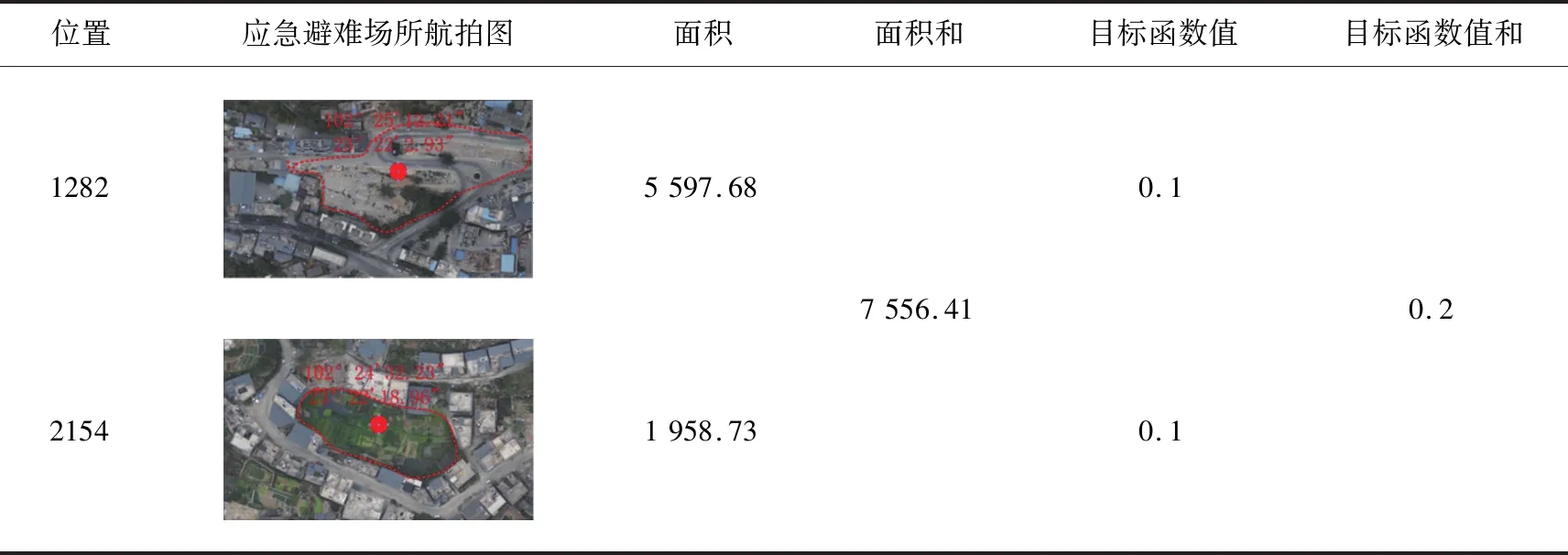
表2 应急避难场所选址结果Table 2 The results of emergency shelter site selection

4 讨论

4.1 穷举法对比分析

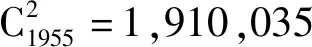
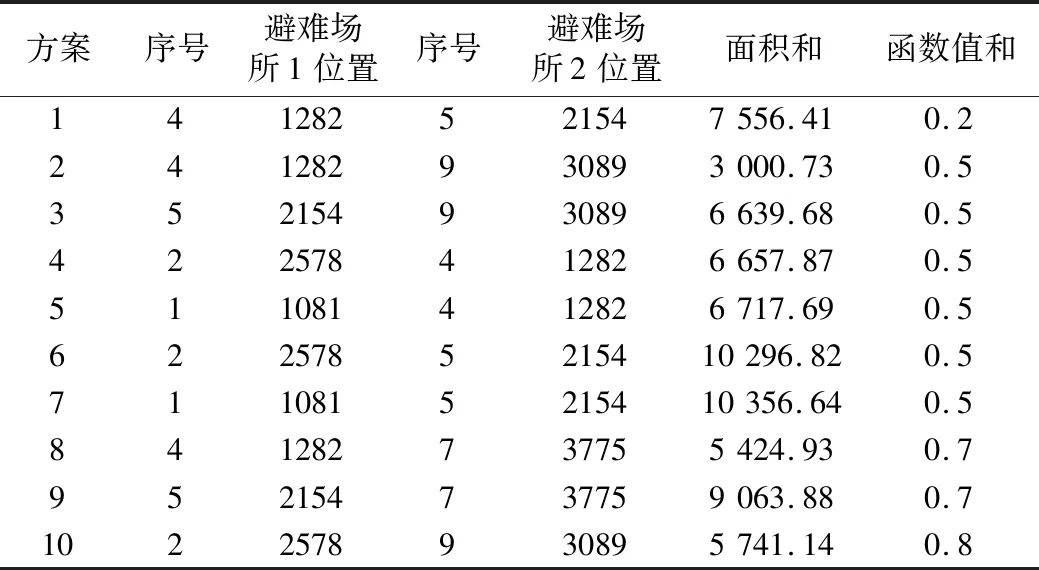
表3 前10组组合方案的函数值和面积Table 3 Function values and areas of the top 10 combined schemes

将以上10组穷举法选址结果进行相似位置叠加显示，得到如图12所示穷举法应急避难场所选址结果，其中序号为4(1282)和5(2154)的应急避难场所叠加次数最多，并且与基于蚁群优化算法的应急避难场所选址位置布局相似。结果表明，设置合适的算法参数，可使模型求得最优解，并且计算时间远远优于穷举法。

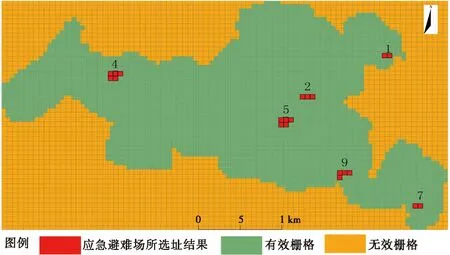
图12 穷举法应急避难场所选址结果Fig.12 The results of emergency shelter site selection of exhaustive method

4.2 实地调研对比分析

本文还采用实地调研的方式进行验证，将红河县城区除现有应急避难场所以外面积大于1 000m2的公园、绿地、广场提取出来，如表4所示，共计10个可待建应急避难场所空地。

表4 候选应急避难场所图片Table 4 The images of candidate emergency shelters

将10个待建应急避难场所位置信息与栅格图11进行位置匹配，得到图13(a)所示待建应急避难场所栅格图。将5个影响应急避难场所选址指标作为底图，叠加位置分布后进行显示，得到图13(b)底图为离现有应急避难场所距离栅格图，图13(c)底图为离高层建筑物距离栅格图，图13(d)底图为人口分布栅格图，图13(e)底图为离主干道距离栅格图，图13(f)底图为道路应急疏散指数分布图。从图13(b)中可以看出除应急避难场所3、8、10离现有应急避难场所较近以外，其余符合选址标准；从图13(c)中可以看出应急避难场所3、6、7、9、10属于高层建筑物影响范围内不符合选址标准，其余符合选址标准；从图13(d)中可以看出10个应急避难场所均处于人口密集区域附近均符合选址标准；从图13(e)中可以看出应急避难场所1、2、6、7、8、10离主干道距离大于100m不符合选址标准，其余符合标准；从图13(f)中可以看出应急避难场所6、8道路应急疏散指数较大不符合选址标准，其余从不同程度上符合选址标准。综上所述可得到应急避难场所4、5选址条件优越，与基于蚁群优化算法的应急避难场所选址结果相同，但实地调研选址方式相对于选址模型耗时较多，并且需要人工处理大量数据。

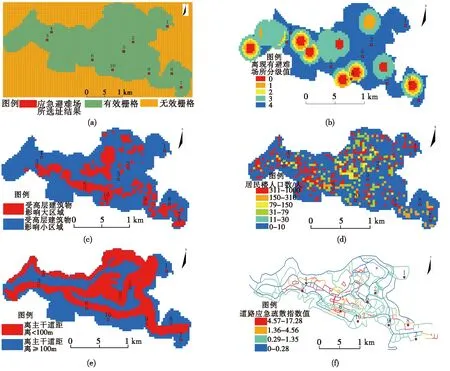
图13应急避难场所选址结果分布图(a)、离现有应急避难场所距离分级图(b)、离高层建筑物距离分级图(c)、人口密度分级图(d)、离主干道距离分级图(e)、应急避难场所选址结果道路风险指数分级图(f)
Fig.13 Emergency shelter site selection results distribution map(a)、the grading map of distance from existing emergency shelter(b)、the distance grading plan for tall buildings(c)、the grading map of population density(d)、the distance grading plan from main road(e)、the emergency shelter site selection result road risk index(f)

5 结论

(1)本文通过改进的蚁群优化算法、ArcGIS技术、遥感技术和选址指标相结合的方式，依据研究区域实际情况选取了8个应急避难场所选址指标，建立基于蚁群优化算法的应急避难场所选址模型。以云南红河县城作为研究区进行模型选址，采用穷举法与实地调研方式进行验证。其中引入道路应急疏散指数(道路宽度、电阻系数、道路节点度、行人逆流、高层建筑物的威胁)，有效增强避难场所选址的实时性、准确性、高效性以及选址结果的直观性和可视性。此外，ArcGIS 数据参照同一空间坐标系，利于集成化解决不同领域共享数据和结果的问题。

(2)在传统的选址方法中，通常采用ArcGIS中两个目的地之间的直线距离或者道路网络分析方法，计算得到每个群众疏散到应急避难场所需要的时间。但在疏散的紧急状态下会遇到道路的突发情况，比如行人逆流、救援队伍进入等等，因此本文提出道路应急疏散指数，相比于传统选址方法，能有效的优化、适应蚁群算法选址模型，对提高应急避难场所选址精确度和效率具有重大的意义。