基于CLSVSM的惩罚性矩阵分解及其在文本主题聚类中的应用

牛奉高，冯世佳，黄 琛

(山西大学数学科学学院，山西 太原 030006)

0 引 言

大数据时代下，信息量飞速增长，通过人工方式快速地在资料中查找有效信息难上加难。文本主题聚类发挥着不可忽视的作用，它是将一个文本集合划分成若干互异的簇，从而使每个簇内文本之间的相似性较大，而互异簇文本之间的相似性较小[1]。文档中包含的知识相当丰富，聚类之前首先要把无结构的文档知识表示为计算机可以识别的数据形式[2]。经典的文本表示模型是由Salton[3]提出的向量空间模型(VSM)，其文本空间是由一组正交向量所构成的向量空间[4]，但其忽视了词与词之间的语义关系，导致文本主题聚类精度不高；Wong[5]针对这一问题提出了一种广义向量空间模型(Generalized Vector Space Model， GVSM)，挖掘了词之间的共现信息，但仍未充分提取语义信息；牛奉高等[6]通过共现分析方法深度挖掘词之间的潜在语义，提出了一种共现潜在语义向量空间模型(Co-occurrence Latent Semantic Vector Space Model， CLSVSM)，其聚类效果优于VSM。然而，模型的维数较高，致使数据稀疏和计算复杂这一问题依旧存在。因此，对其进行降维处理是非常必要的。

矩阵分解对数据降维非常有效，通过矩阵分解得到原数据矩阵的低秩近似，是对原始数据内在结构特征的刻画[7]。常见的一种矩阵分解工具是奇异值分解，是很多经典算法(如潜在语义分析、主成分分析)的求解方法，在文本挖掘领域被广泛应用。但是一般情况下分解后的左右奇异向量中的元素为正或为负，没有0元素，此时结果通常是不能解释的[8]。于是，本文将惩罚性矩阵分解应用于文本资源，构建语义核来实现降维的同时提高聚类算法的性能。

惩罚性矩阵分解(Penalized Matrix Decomposition, PMD)是在2009年由Witten等[8]提出，并将其应用于稀疏主成分分析和典型相关性分析。此后，学者们将该方法应用于多个领域。Zhang等[9]利用PMD从微阵列数据中发现转录模块。Zheng等[10]将PMD应用于基因表达。王娟等[11]提出了一种基于PMD的文本软聚类算法，并用实验证明该方法在信息检索方面的效果。Liu等[12]提出了利用PMD稀疏方法来提取核心基因，并用实验证明了该方法的有效性。俞仙子等[13]提出了一种基于PMD的文本核心特征词提取方法，并证实得到的核心特征词更易被解释。邵作运等[14]实现了共词分析中基于PMD的特征词提取、软聚类和可视化。随后，Liu等[15]引入了全局散度矩阵，提出了基于类别信息的PMD。惩罚性矩阵分解，是对向量进行稀疏化惩罚，随后这种方法被广泛应用[16]。

1964年，Ajzerman等[17]探究势函数时，在机器学习中引进核函数，它的引入在一定程度上促进了支持向量机(SVM)的进步。此后，许多学者将核函数方法与聚类算法相结合[18]。核方法将数据对象映射到更高维的空间，然后利用它们变换之后向量之间的相互信息(如内积)来构建分类、回归和聚类。因此，用核函数方法应对高维的问题是有显著成效的。

计算文本之间的相似度时，增添语义联系，可以明显地提高聚类性能。因而，各个领域探究时将文本语义的核函数视为重点。2000年Siolas等[19]提出了语义核(Semantic Kernel)的观点，并将其作为支持向量机中的基础核。2002年，Cristianini等[20]基于LSA的思想，提出了潜在语义核。2005年，Mavroeidis等[21]给出了语义核函数的正式定义，并基于共现分析的理论构建了广义向量空间核。2010年，张玉峰等[22]又提出了基于WordNet的语义核函数。2013年，Nasir等[23]提出了语义平滑VSM，并实现了语义核的创建。2014年，Kim等[24]提出了一种语言独立语义(LIS)核，它能够在不使用语法标签和词汇数据库的情况下有效地计算短文本文档之间的相似度。2017年，Wang等[25]提出了语义扩散核，不仅考虑了共现知识，还利用了文档的类知识。2019年，徐炎等[26]结合HowNet通过本体库和内部统计特征构造语义核。

本文受以上PMD及语义核函数的启发，基于CLSVSM研究惩罚性矩阵分解，其有助于挖掘文本数据的本征结构，增强可解释性，提高了文本表示模型的聚类效果。基于PMD构建语义核函数，具体是依据CLSVSM得到的篇词矩阵应用PMD方法对特征向量进行稀疏约束，由此得到的词与词之间的共现矩阵是稀疏的且体现了核心特征词的语义信息。最后通过共现分析理论构建语义核，进一步挖掘了数字文本资源之间的语义关联，降低了计算复杂度。将本文提出的方法应用于数字文本资源的主题聚类研究，实验结果表明，该方法在降低矩阵维数的同时，减少了计算复杂度，提高了文本资源主题聚类的精度。

1 相关知识概述1.1 共现潜在语义向量空间模型

CLSVSM主要应用每个特征词之间的最大共现强度，对传统形式下高维稀疏0和1权重的文本表示模型进行语义补充。CLSVSM[6]构建过程如下：

首先，设有n篇不同文献组成的文献集，这些文献共有m个互异的特征词，组成特征词集，建立“篇-词”矩阵A=(aij)n×m。A中的元素取值采用布尔权重的方法。

其次，特征词之间的共现矩阵表示为C=AT·A，相应的共现强度矩阵计算公式如下：

(1)

最后，引进指标集Ii1={j|aij=1}，即所有aij=1的特征词j的集合。据此构建CLSVSM，其表达式为：

φ:diφ(di)=(qi1,qi2,qi3,…,qim)T∈Rm

(2)

其中，

(3)

1.2 惩罚性矩阵分解

Witten等[8]详细给出了惩罚性矩阵分解的计算规则，对矩阵Xn×p进行SVD，公式如下：

X=UDVT

(4)

其中，U和V这2个向量是正交的，D是奇异值矩阵。

PMD的方法是在U或V上进行约束，其目标函数为[8]：

(5)

其中，u是U的一列；v是V的一列；d是D的对角线元素；‖‖是Frobenius范数；P1和P2是凸惩罚函数，它们可以使用多种形式[8]。

单因子PMD的目标函数为：

(6)

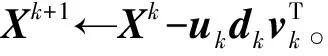
1.3 语义核

2005年Mavroeidis等给出了语义核的正式定义，对于文本表示模型，在构建语义核函数时，可以先对其进行简单的线性映射φ:φ(di)=Sdi,i=1,…,n,其中S称为相似性矩阵，表示文档中特征词的信息，S可以选择任何恰当形式的矩阵，得到语义核函数[21]，公式如下：

(7)

其中，矩阵P是对称的，Pij表示特征词i与j间的语义关系[21]。因此，特征词空间的语义关系也可以通过语义核函数来度量，不同的矩阵S构造的语义核函数也是不同的。

2 基于CLSVSM的惩罚性矩阵分解

2.1 利用PMD的理论分析

本文利用PMD的目的：1)对特征词样本施加惩罚，提取核心特征词，进而计算篇词矩阵的K-秩近似，重建原始文本数据；2)基于该分解方法构建语义核函数，进一步挖掘核心特征词之间的语义信息，降低文本表示模型的维数，减少计算复杂度。由于PMD基于稀疏约束，经过约束的大多数系数都会变成0，从而凸显出特征词样本的最主要部分，使高维矩阵更加容易识别和解释[27]。

对于CLSVSM中的n×p维的篇词矩阵X，用PMD将其分解成2个基本的矩阵U和V，即X～UV,它们分别是左奇异矩阵和右奇异矩阵，左奇异向量{uk}是矩阵U的一列，代表了相应特征词样本的表达模式，右奇异向量{vk}是V的一列，代表了特征词样本，如图1所示[12]。

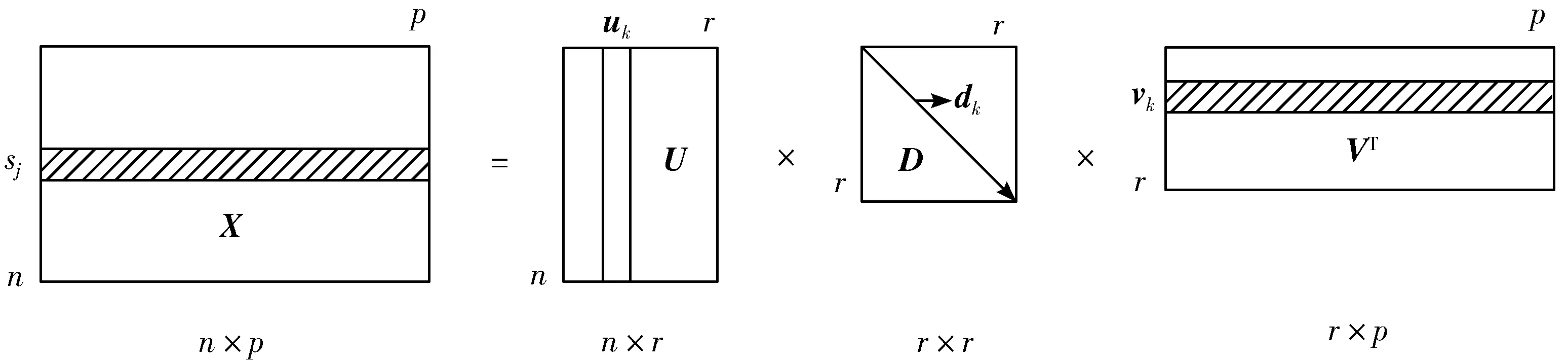
图1 基于PMD的文本数据分解模型

通常，文本数据的特征样本定义为原始样本的线性组合，特征样本应包含数据的本征结构。换句话说，每篇文档都可以看成特征样本的线性组合，因此可以在稀疏过程中找到能够表达所有文本的核心特征词，代表了所研究领域的热点及方向[14]。因此，本文通过计算原始文本数据的K-秩近似，提取数据的本征结构，使文本表示模型更合理、恰当，将其应用于文本主题聚类中，检验其聚类效果。

根据图1，矩阵X的第j行元素Sj，即p维的向量，是特征词样本{vk}的线性组合，计算公式如下：

(8)

然而为了重建原始数据，需要特征词样本，即p维向量。如上所述，X的第j行元素构成p维向量Sj。因此，样本Sj可以由特征词样本{vk}来表示。也就是说，在文本表示模型中，可以使用特征词集，即核心特征词，来代表文本。

2.2 基于PMD构建语义核函数

首先基于CLSVSM进行文档表示，其对应的“篇-词”矩阵表示为：

(9)

建立语义核函数的重要步骤是寻找相似性矩阵S。本文对“篇-词”矩阵X进行惩罚性矩阵分解，由前述可知，奇异矩阵V就反映出了篇词矩阵中相应的特征词中的信息。取前k个特征值对应的特征向量vk，使得抽取的信息能最大程度地解释特征词的信息[28]。

针对特征词向量非稀疏性导致解释性差的问题，本文基于PMD准则，在v上实施惩罚：P2(v)=‖v‖1≤c2，不对u进行约束，其目标函数为[8]：

(10)

k(di,dj)=φT(di)VkVkTφ(dj)

(11)

简称其为PMD_K，得到的核矩阵为：

K=XVkVkTXT

(12)

矩阵(12)也反映了两篇文本之间语义关系的相似性。基于PMD的语义核构建不仅对核心特征词间的语义信息进行合并，而且共现矩阵具有稀疏性，使得运算简便，避免了高维空间的复杂运算。

3 实验设计及结果分析

3.1 实验数据

文献数据向量表达相对比较准确，因此本实验在中、英文3类文献数据上进行。

中文数据均来自CNKI，第一类收集于信息科学下的3个学科，分别为“出版”“图书情报与数字图书馆”和“档案及博物馆”，简略处理，最终获得文献896篇，其中包括“出版”299篇、“图书情报与数字图书馆”298篇、“档案及博物馆”299篇，同时共获得2024个关键词。第二类是多类别不均衡数据，采集于5个类别，简略处理，最终获得文献共1650篇，其中“出版”360篇、“档案及博物馆”330篇、“图书情报与数字图书馆”380篇、“科学研究管理”300篇和“宏观经济管理与可持续发展”280篇，共包含关键词4256个。

英文数据收集信息来源于Web of Science，类别分别是“computer science information system”、“management”、“computer science interdisciplinary application”这3种，一共获得411篇文献，1889个文献关键词。

3.2 评价指标

对数据使用聚类算法聚类后，对结果进行优劣判断，本实验选择的评价指标是纯度(purity)、熵值(entropy)、F值(F-measure)。

本文将实验的文献分为k个类别，将其标记为Lj(1≤j≤k),使用聚类算法对文献集进行聚类后获得k个簇，将其标记为Cr(1≤r≤k)。假如实验的文档有n篇，类Lj中共有nj篇文档，簇Cr中共有nr篇文献，其中无差异的文献有nrj篇。评价指标纯度、熵值的计算公式如下[6]：

(13)

(14)

定义每篇文献i的准确率和召回率，计算公式如下[6]：

Pr=nrj/nr,Rj=nrj/nj

(15)

采用每篇文献的准确率和召回率的平均值表示聚类结果总的准确率和召回率，分别简记为P和R，计算公式如下[6]：

(16)

单独使用准确率或者召回率时，不能够全面衡量聚类效果的优劣。为了平等地看待准确率和召回率的影响，采取准确率和召回率的调和平均，记为F，计算公式如下[6]：

(17)

3.3 实验过程

本文利用各种方法进行文本主题聚类的主要实验步骤如下：

Step1将采集到的数据通过VSM、CLSVSM进行文档表示得到篇词矩阵，作为实验的基础矩阵。

Step2通过对基础矩阵进行SVD分解，求得矩阵的秩值，3类数据的秩分别为890、1642和405。

Step3基于CLSVSM构建核函数，详细构造方法见文献[28],使数据中的前K个特征值的和与所有特征值和的占比达到95%，将之简称为95%CLSVSM_K。

Step4基于CLSVSM的惩罚性矩阵分解研究，实现原始文本数据的重建，详见第2.1节。

Step5参考第2.2节，基于PMD构建语义核函数，得到核矩阵。

Step6通过以上步骤进行计算求得矩阵后，使用gCLUTO工具包中的Repeated Bisection(重复二分法聚类)、Direct(直接聚类)、Agglomerative(凝聚聚类)和Graph(图形聚类)这4种聚类算法进行聚类[29]。

实验过程如图2所示。

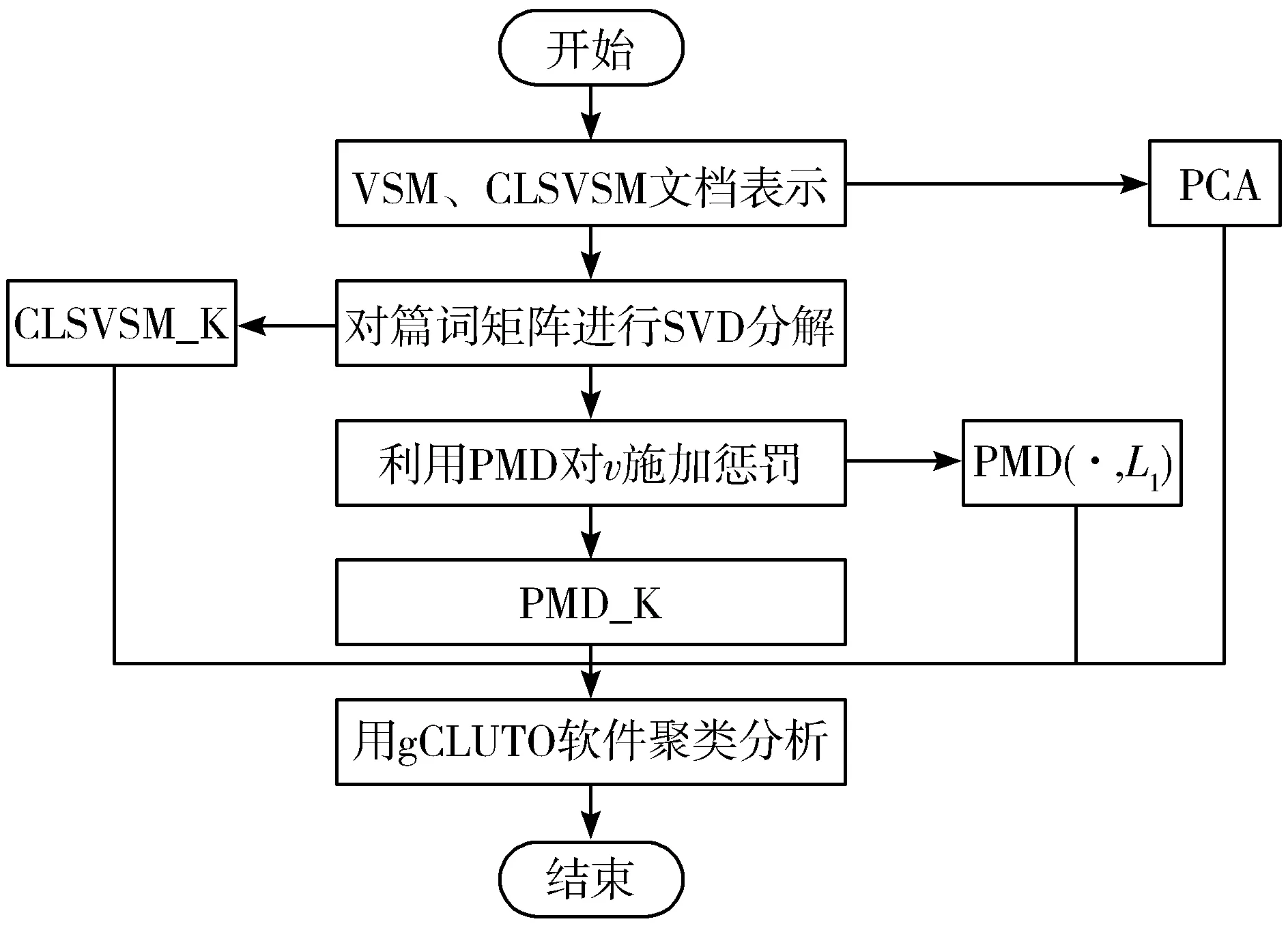
图2 实验流程图

3.4 实验结果

为了检验本文方法具有广泛适用性和有效性，本文将PMD(·,L1)和PMD_K这2种方法与经典的文本表示的降维方法PCA、95%CLSVSM_K进行实验比较。在VSM、CLSVSM这2个模型上用4种聚类算法对中、英文数据集分别进行30次实验，通过多次实验求得3个指标的均值来对聚类结果进行评价。熵值越靠近0，纯度和F值越接近1，表明聚类效果越好[6]。在第一个中文数据集上，分析对比结果如表1所示。表1中将实验的最优结果用※符号标记。

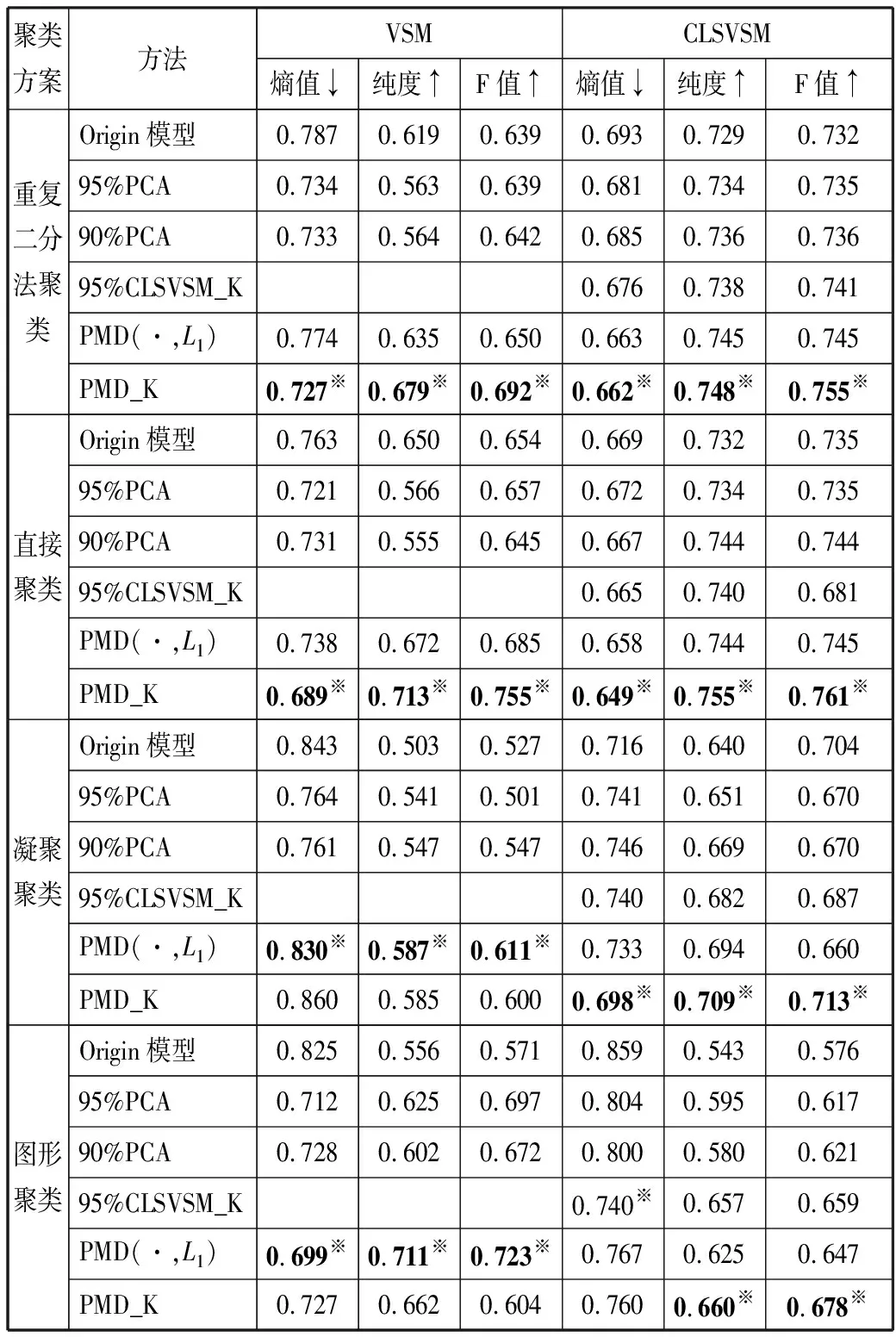
表1 第一个数据集在不同聚类方案上的聚类结果比较

从表1可以看出，对于2种不同的文本表示模型，不管用哪种聚类算法进行实验，本文提出的基于模型的PMD方法和构建的语义核，明显比原始的方法聚类效果更优。横向观察，除了图形聚类算法，基于CLSVSM上不同方法的各评价指标的结果均优于VSM。

利用重复二分法进行聚类，基于CLSVSM的惩罚性矩阵分解方法，即PMD(·,L1)实验比CLSVSM、95%PCA实验，纯度和F值各自增长率分别为2.2%、1.8%和1.5%、1.4%。在VSM模型上，构建语义核方法(PMD_K)与VSM、95%PCA、PMD(·,L1)方法比较，纯度达到0.679，分别提高了9.7%、20.6%和6.9%。同理，可以看出，在凝聚聚类和图形聚类算法上，本文提出的2种方法的优势。其中，直接聚类算法的结果表现最好。

由图3可知，基于CLSVSM，PMD_K在30次实验中的纯度明显高于95%CLSVSM_K曲线，同时也较其他曲线稳定，并处于最高位置，且与95%CLSVSM_K相比，F值提高21.9%。基于CLSVSM的惩罚性矩阵分解曲线在一定范围内处于较高位置，相较于CLSVSM、95%PCA曲线波动幅度较小。

图3 直接聚类下基于CLSVSM各个方法的纯度折线图

由图4可知，在VSM上，基于PMD构建语义核和基于VSM的惩罚性矩阵分解曲线明显高于其他曲线，且相较VSM，结果相对稳定。充分说明了本文方法的聚类性能更强。

图4 直接聚类下基于VSM各个方法的纯度折线图

表2 在第二个多类别数据集上的聚类结果比较

表2是在以上实验中表现较好的CLSVSM上，利用直接聚类算法进行实验的聚类结果比较。可以看出，在聚类效果上，各种方法在该多类别不均衡数据集上与第一个数据集上的表现基本一致。其中，基于CLSVSM的PMD实验的纯度和F值分别较CLSVSM提高了12.1%和13.9%，而熵值降低了15.0%。

之后，又在英文数据集上进行了多组实验，进一步检验方法的适应性和稳定性。采用以上实验中聚类结果较好的直接聚类算法，结果如表3所示。

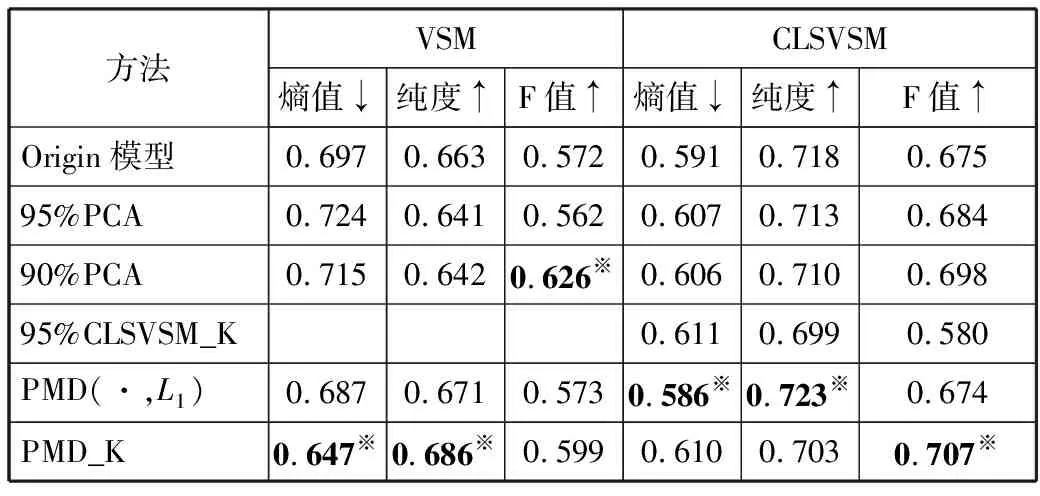
表3 在英文数据集上不同方法的聚类结果比较

从表3可以发现，本文方法的聚类效果依旧比较明显。在CLSVSM模型上，PMD_K方法求得的F值比95%CLSVSM_K求得的F值提高21.9%。且在各个评价指标下，数据实验的聚合效果均好于比较实验。

通过以上分析，使用PMD方法后的聚类效果明显较优，尤其是基于PMD构建语义核的聚类结果更优，原因在于进一步挖掘了词间的语义信息，并将其合并，降低了矩阵的维数，减少了计算复杂度。基于CLSVSM的惩罚性矩阵分解研究，通过提取核心特征词来重建文本数据，新的篇词矩阵代表了原始数据的本征结构，提高了文本表示模型的可解释性。在文本主题聚类应用中的结果显示，可以有效提高聚类性能。因此，可以把其推广应用到信息检索等领域，实现数字文献资源的高维聚合。

4 结束语

针对现有的文本表示模型稀疏和高维的问题，本文将惩罚性矩阵分解方法应用于CLSVSM，对特征词样本进行稀疏约束，计算矩阵的最优K-秩近似，挖掘数据的本征结构。通过共现分析理论，基于PMD构建的语义核函数(PMD_K)，深度提取核心特征词之间的语义信息，实现同义词的合并，在引入共现信息的同时又降低了文本表示的维数，减少了计算复杂度。实验结果表明，该方法与原始方法相比增强了文本主题聚类的效果，可以应用于文本资源的检索、文本分类和知识发现等领域。

今后，笔者将继续深入研究惩罚性矩阵分解方法，探索不同的惩罚函数的最优解，并比较其应用于不同数据集上的泛化性，以便用更合适的方法对数据矩阵进行降维，实现文本的有效聚类。