基于改进Floyd算法的网络舆情监测

李金泽,武文豪,李开航

(1.中国人民警察大学,河北 廊坊 065000； 2.济南大学,山东 济南 250000； 3.山东青年政治学院,山东 济南 250000)

0 引 言

随着互联网技术的不断发展，人们获取信息的方式已经突破了时间空间的限制，在网络大环境中，任何信息都可以在电脑上被查询到[1-3]。互联网信息具有多样化与全球性的特点，并且拥有着前所未有的独特环境[4]。在这个独特的环境中，人们逐渐适应了这种新型的传播介质，开始愿意在互联网中表达自己的意愿，网络舆情已经逐步开始替代传统的社会舆情[5]。网络舆情反映了互联网时代的独特舆论，其反映的是人们在互联网的意愿，属于舆情的一种表现形式，也是舆情在特殊渠道上的表达[6]。因为网络舆情是建立在互联网的互动性与开放性的基础上，所以网络舆情不仅拥有自身的独特性，同时也具有传统舆情的特征。舆情通常被理解为民意的综合表达，有时也会被描述为舆论的综合表现[7]。无论怎样对舆情进行理解，其大致的含义都不会有偏差，即群众的意见与态度。互联网发展至今，仍然有较多的政府工作人员还不适应互联网的应用，并不重视网络舆论，以致在网络舆情检测与收集上的体制不完善，并不能及时应对网络舆情危机，这些都阻碍了政府管理能力和办公效率的提升[8]。网络舆情监测工作的革新与发展已经上升至对负面舆情信息载体类型分布及舆情内容构成的研究,进而对我国政府舆情工作存在的不足提出建议[9]。为了使我国政府机关在互联网环境中的舆情管理能力得到提升，国内学者通过应用先进的监控技术与分析方法，以达到掌握群众思想动态的目的[10]。国外对网络舆情监测方面的研究起步较早，舆情分析技术与热点发现，目前国外对话题的跟踪与检测，以及文本倾向性分析技术是当前最为常见的2大内容。因此，本文探讨基于改进Floyd算法的网络舆情监测，重点加强对网络舆论的分析，达到能够应对社会突发事件的能力，保证社会的稳定发展。

1 Floyd算法的内涵

由于本文主要是针对URL参数和链路的耗时进行优化，从而达到全局优化的目的，该方式与Floyd算法根据某一节点求取另一节点最短路径的方式不谋而合。对于Floyd算法的基本思想而言，应该从单源最短路径和任意定点间的最短路径入手进行探讨[11]。若存在赋权有向图G=(V,E)，将G中的弧aij=(vi,vj)上的权定义为W(aij)=Wij，将s和t分别定义为G的起点和终点，设G中s到达t的路程为p，定义p内有弧的权之和为p的权，记作W(p)，那么:

(1)

再设G中s到达t的一条最短路程为p*，那么

W(p*)=min{W(p)|p为s到t的路程}

(2)

其中，取p值的最小值，即s到t的最短路程为p*，那么W(p*)则表示s到t的最短距离。在赋权有向图G中，求s到t的最短路程就是在求解最短路径问题。

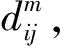
Floyd算法的计算开始于D0，通过D0对D1进行计算，再通过D1对D2进行计算，以此类推，最终通过DN-1计算出DN。计算方式如下：

(3)

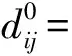
2 基于改进Floyd算法的模型构建

2.1 基于改进Floyd算法的控制策略

在分析网络舆情时，首先要对网络文本进行抓取，并对行为特征进行分析，将不同的行为特征进行分类，以根据不同的行为类型进行网络舆情检测[15]。标准Floyd算法是将节点之间的权值作为运算变量，对抓取相应文本并进行分析的这种较为复杂的网络舆情检测似乎有些不合时宜[16]。所以，本文对Floyd算法进行改进。标准Floyd算法的变量具有单一性，以路径作为计算结果，并在准确的数据源中提取出数据中的热门主题，分析其潜在舆情[17]。本文的改进算法将权值设定为可变的，依据系统的实时变化对权值进行动态调整，同时节点有一定的灵动性，并附带节点信息。Floyd算法对最短路径进行计算时，主要是运用每个节点的弧度值。但在进行网络舆情的检测时，要依据每个节点信息和网络的实时延迟信息对最小耗时进行获取，使得媒体信息匹配与搜索的效率进一步提高[18]。网络舆情检测系统可以较好地统筹协调子系统和整体系统，进而优化系统的性能，有效的早期监测预警是防范突发事件网络舆情蔓延扩散的前提条件[19]。

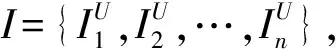
(4)

对子系统进行实时定位时，要根据当前网段与单元智能体的反馈信息进行确定，相邻子系统会接收到子系统的实时定位信息，其他相邻的子系统也会根据这个原理评估子系统之间的相互关联性，以对数据信息进行构建，提高数据查询的效率[21]。具体的表达式如式(5)：

IS=h(UNS,NNL,CCS,Γi,j)

(5)

其中，IS表示网段智能体定位信息；CCS表示内容主题集；NNL表示网络延迟值；UNS表示网络稳定值。网段相邻的智能体可以协调控制相邻的网段，可以在宏观上将网段智能体看作是单个的节点，而相邻节点可以用相邻网段智能体来表示[22]。如式(6)所示，对每个弧度的耗时进行计算后，以对搜索方案进行合理的制定。

(6)

系统整体协调策略主要是在获取子系统信息后，先对子系统的定位信息进行获取，并对比子系统之前的定位信息。根据定位信息的差距大小，分别作出相应的标记。由于每个子系统在全局智能体中，都可以看出是节点，因此各个子系统的耗时计算方法如式(7)：

(7)

2.2 Floyd改进算法在网络舆情中的应用

如图1所示，网络舆情图是由多个节点组成，图1中共有9个URL节点。

图1 网络舆情图

节点Ui到Uj所需要的时间可以用单权值βi表示，单权值βi又由2个节点间的差异所决定，如式(8)所示：

(8)

一般情况下，采用相邻URL地址的弧度来表示相邻节点间的Γi,j。对于节点1、节点2，Γi,j为节点1与节点2间的弧度大小，并且在不停地进行变化，主要由β1、β2的取值来决定，如式(9)所示：

(9)

若采用ΓA,B表示搜索起点A到终点B的耗时，那么由Floyd算法推导出Γi,j的几何形式如式(10)所示：

ΓA,B=f(Γ1,2,…,Γi,j)

(10)

在某些情况下，αi,j和ΓA,B也会有对应的关联，如式(11)所示：

ΓA,B=k×αi,j

(11)

对于Floyd算法在改进后的文本分析，若存在字符串“你在哪里where”，将字符串看作是5个线性的节点，分别为“你”“在”“哪”“里”“where”5个节点，如图2所示。

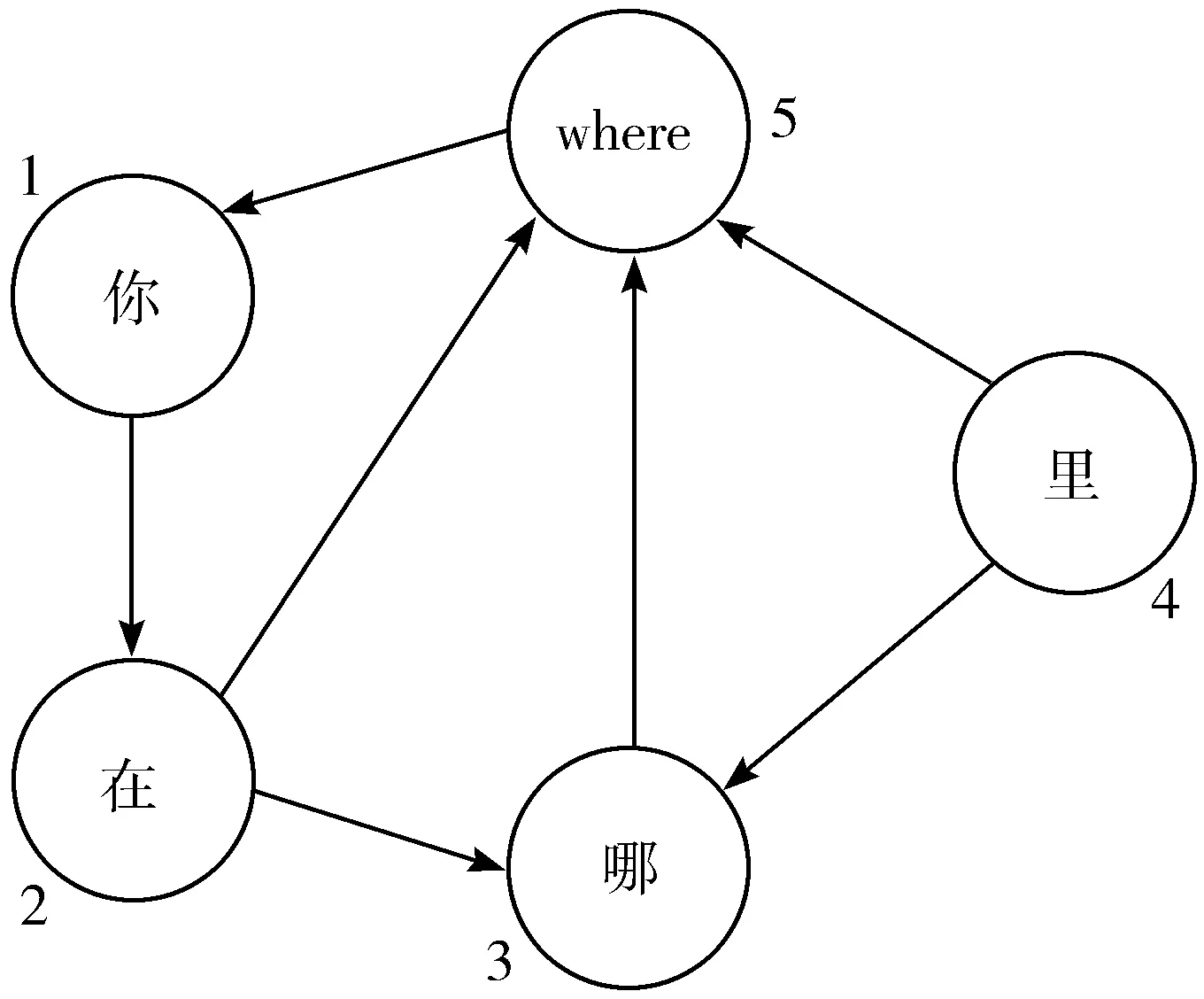
图2 网络舆情文本分析图

图2中，节点1、节点2不能构成词语，因此相关性较低，α取值较小；节点3、节点4则构成词语的可能性较高，因此相关性也较高，α取值较大。所以，节点路径存在3种可能性，分别为1→2→5、1→2→3→5、1→2→3→4→5。1→2→5路径虽然比较简单，但是具有较高的扩展性；1→2→3→5要应用算法的记忆功能，尤其是要预先知道节点3、节点4属于词语的情况；1→2→3→4→5是耗时最长的算法，但是路径却最为可靠。

影响网络舆情监测技术的因素主要包括URL文本重用率、文本的正确率以及文本的有效率[23]。URL的有效率可以体现抓取URL地址时的效率和准确率，反映了算法的有效性，表达式如式(12)所示：

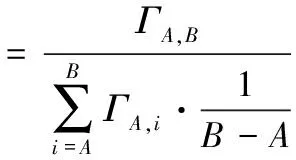
(12)

对URL文本进行分析衡量的一个重要指标就是URL文本的准确率，其表达式如式(13)所示：

(13)

URL文本重用率反映了各个URL之间的文本耦合度，若重用率低，则耦合度也低，表现出的性能就越好。其表达式如式(14)所示：

(14)

对于网络舆情系统的评价而言，不但要评价不同实例间表现出的不同性能，也要对不同算法的时效性进行对比[24]。

时效性主要对系统的便捷系数进行衡量，以及体现算法的时空复杂度情况，其表达式如式(15)：

(15)

3 实验与分析

本文将本地实验机房的主机作为实验环境，并采用VLAN对子网进行划分，赋予各个主机不同的子网号与IP。创建测试网页在不同的IP和网段上，其中包括了链接、视频、音频、图片以及文本各种媒体信息。结合本文建立的模型，将模型参数定义为各种媒体信息。

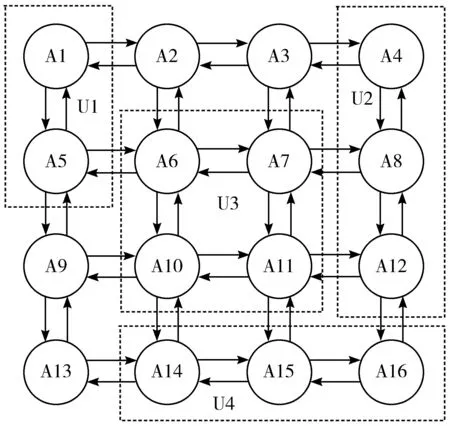
图3 网络舆情监测系统建模图

如图3所示，实验机房中包含了16台主机，应用VLAN将其划分成4个子网，网段U1包括了A1和A5主机，网段U2包括了A4、A8和A12主机，网段U3包括了A6、A7、A10和A11主机，网段U4包括了A14、A15和A16主机。利用以上实验条件对本文提出的算法模型进行验证。首先，应用Floyd改进算法对URL网页中的文本进行提取，并预处理获取到的文本信息，最后通过Floyd改进算法计算出实验结果。

表1 对比Floyd算法改进前后的时效性

如表1所示，改进后Floyd算法的时效性明显优于改进前的算法。本文的网络舆情相关数据均来自人民网和正义网正式发表的相关资料，以对提出的模型算法进行验证。

表2 传统single-pass、聚类算法、基于Floyd改进算法的分析结果对比 单位：%

表2针对3种不同指标对传统single-pass算法、聚类算法以及基于Floyd改进算法进行了对比，发现Floyd改进算法的各项指标均明显优于其他算法。

如图4所示，若只存在案例1和案例2时，案例较为精简，Floyd算法改进前后的差异性较小。但随着案例的增多，运算逐渐趋于复杂，Floyd算法在改进之后的时效性显著优于改进前。

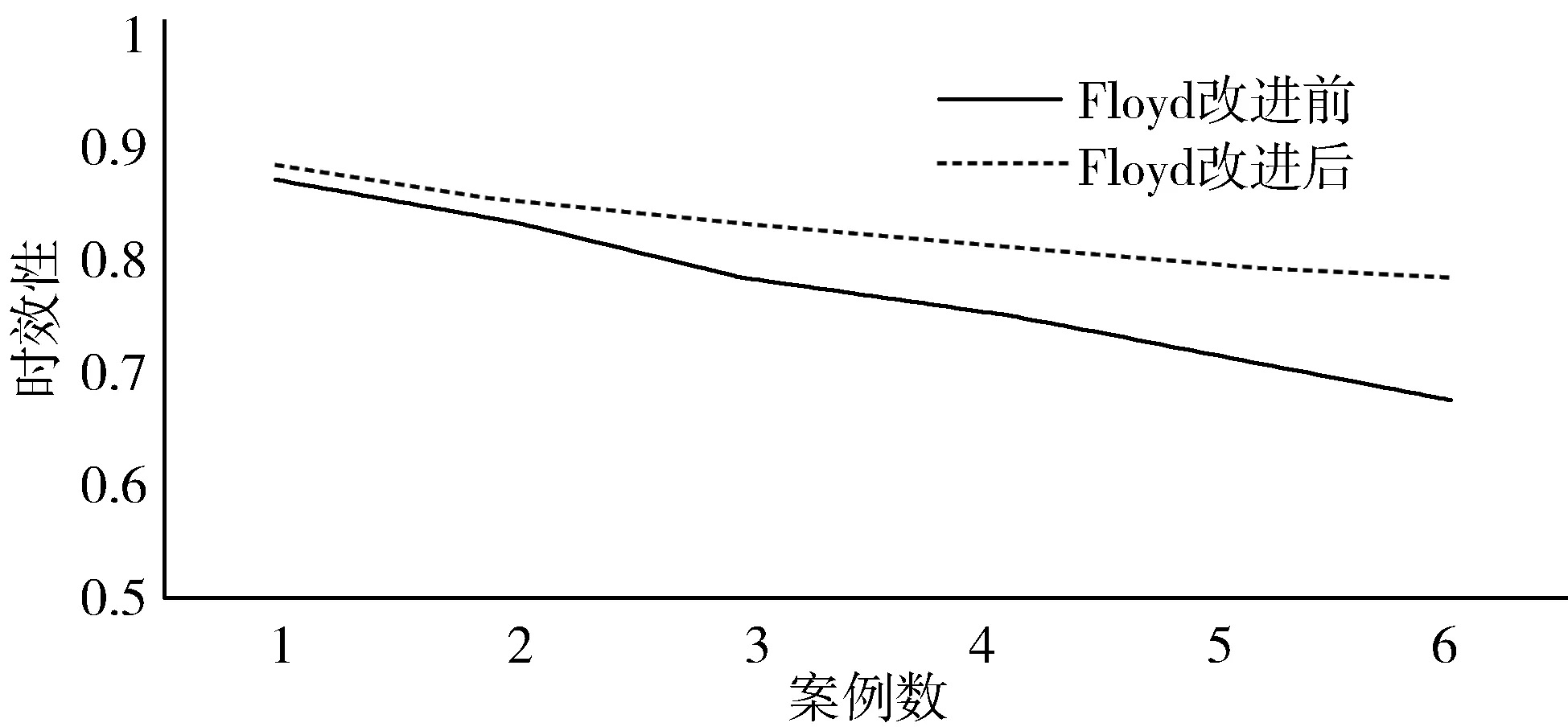
图4 Floyd算法改进前后的时效性对比

如图5、图6所示，在数据组较少时，Floyd改进算法的有效率和准确率明显优于其他算法；随着数据的增加，Floyd改进算法的有效率和准确率优势逐渐变弱，但仍然优于其他算法。

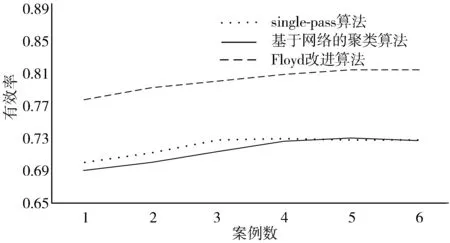
图5 各种算法的有效率对比

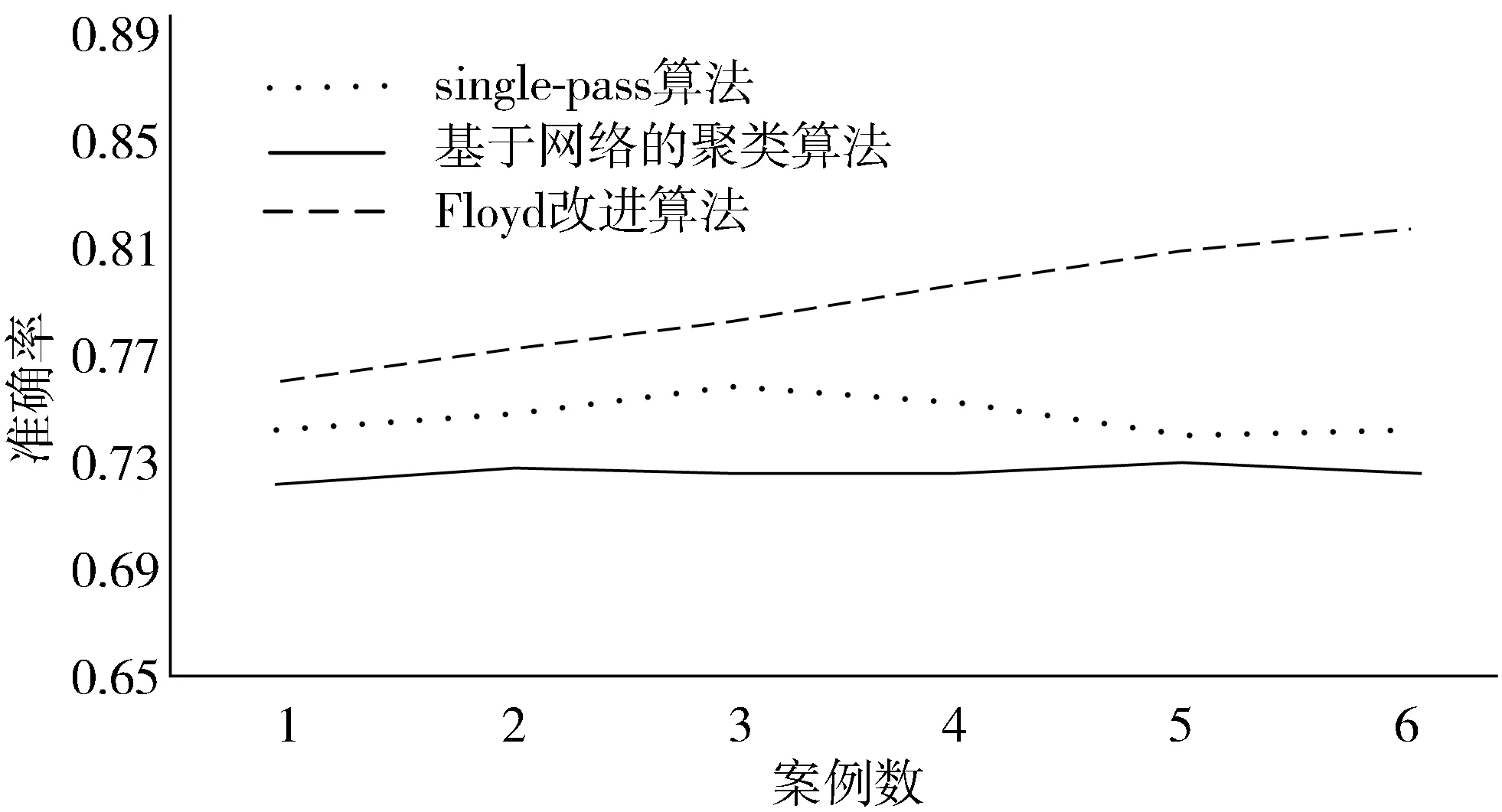
图6 各种算法的准确率对比

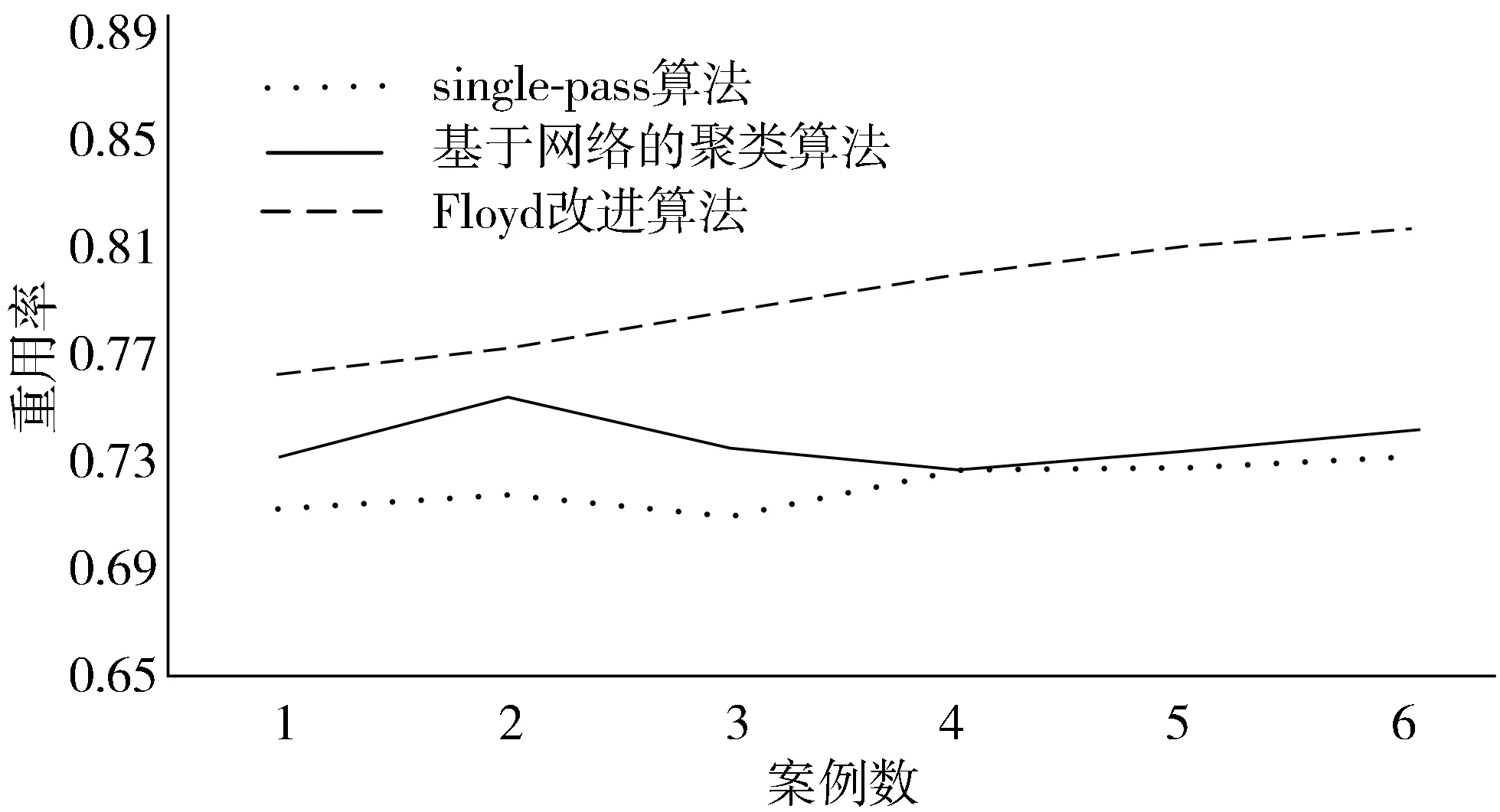
图7 各种算法的重用率对比

如图7所示，Floyd改进算法的重用率明显优于其他算法，但当实验数组达到一定上限时，仍然会出现重用率极限值。

4 结束语

本文在政府舆情监测领域提出了基于Floyd改进算法的控制策略与舆情监测应用模型，并针对3种不同指标对传统single-pass算法、聚类算法以及基于Floyd改进算法进行了对比实验。实验结果表明，Floyd改进算法的各项指标均明显优于其他算法。其中，若案例数较少时，Floyd算法改进前后的差异性较小。但随着案例数的增多，运算逐渐趋于复杂，Floyd算法在改进之后的时效性显著优于改进前；在数据组较少时，Floyd改进算法的有效率和准确率明显优于其他算法。随着数据的增加，Floyd改进算法的有效率和准确率优势逐渐变弱，但仍然优于其他算法；Floyd改进算法的重用率明显优于其他算法，但当实验数组达到一定上限时，仍然会出现重用率极限值。由于Floyd算法自身具有较高的时间复杂度，应用于大数据运算时效果较差，本文对于Floyd算法关于数据量较大时的运算探讨较少，在今后的研究中，会更关注Floyd算法在数据量较大时的改进优化，期望今后在技术上能够突破，开发出更加完善的舆情分析系统。