一种融合多维信息的移动社区发现方法

舒 鹏，杜庆伟

(南京航空航天大学计算机科学与技术学院,江苏 南京 211106)

0 引 言

近年来，随着移动互联网的迅速发展和移动设备的日益普及，已经涌现出不同类型的应用服务，例如Foursquare、微博等社交应用。移动网络中充斥着大量的用户数据，包括社交通信数据、上网信息和轨迹信息等。利用这些信息挖掘大型网络中节点之间的关系和社区结构可以发现用户的行为特征和关联，进而为实现信息的共享和热点推荐等提供智能决策[1]。

社区发现即挖掘网络中存在的群体结构[2]。目前，针对社会化网络领域的社区发现已有许多成果，主要有基于标签传播的算法[3]、基于模块度的算法[4-6]和基于图分割的算法[7]。然而，这些传统的社区发现算法通常仅考虑单一实体的连接结构而忽略了用户间的共同兴趣特征，难以保证社区结构的内聚性。在复杂异质的移动社区网络中不仅包含用户、地理位置、主题内容等实体，还包含用户间的各种偏好关系，如何高效地对复杂异质的移动社区网络进行社区发现成为关键问题。

本文通过分析移动网络使用详单数据(UDR)和移动用户社交数据中的用户间社交关系、地理位置偏好关系和主题内容偏好关系这三维信息分别构建社交相似网络、地理位置相似网络和主题相似网络，然后利用网络融合(Network Fusion， NF)方法融合多维相似关系构建用户相似网络，并运用有界非负矩阵分解(Bounded Nonnegative Matrix Factorization, BNMF)来确定最优的社区结构划分结果。实验结果表明，在复杂异质的移动社区网络中，本文提出的BNMF-NF方法能够高效发现用户社区结构。

1 相关工作

移动社区网络中一组内部紧密联系的用户形成移动社区，社区内部用户节点间的相互作用比社区和外部用户节点的相互作用更强。在移动社区网络中进行社区发现就是识别一系列节点的集合，使得移动用户集合内部的用户节点之间的相互联系更加紧密，而集合与集合间用户节点相互联系更加稀松。目前，社区发现研究已有许多成果，大致可分为以下4类：

1)基于模块度的社区发现算法。模块度是Clauset和Newman[5]提出的评价社区结构的指标，定义为每个社区内边权重与其期望之差的和，模块度越大表明社区结构越明显。基于模块度函数优化的Louvain算法[6]是该类算法典型的代表成果。

2)基于标签传播的社区发现算法。Raghavan等人[8]将节点归属社区抽象为标签，提出了基于标签传播的社区发现算法。

3)基于随机游走的社区发现算法。Rosvall等人[9]提出了基于随机游走的社区发现方法，将随机游走序列中的每个节点进行Huffman编码，同时对社区也进行编码，算法优化目标为2个部分编码的平均描述长度最小化。

4)基于图分割的社区发现算法。Kernighan和Lin提出了基于图分割的KL算法[7]。Girvan和Newman聚焦于社区结构特性提出了另一种基于图划分的GN算法[10]。

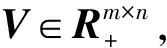
V≈WH

(1)

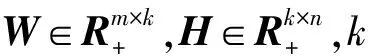
2 融合多维信息的社区发现方法

2.1 移动社区网络模型

移动社区网络中不仅包含用户-用户的社交关系，还包含了用户-地理位置偏好关系和用户-媒体偏好关系。本节根据用户间社交行为和移动网络使用详单数据来构建移动社区网络模型，下面给出具体定义。

定义1用户-用户社交关系网络。用户间的社交行为可简单表示为无向图结构，记为S=(U,O)，其中，U={u1,u2,…,uM}表示用户集，O表示用户社交关系的边集，O={oij|oij=(ui,uj),ui,uj∈U}，其中oij是ui和uj之间表示社交关系的边。

移动网络使用详单数据的格式如表1所示，移动用户通过基站访问网络内容时基站侧会进行记录，其中，开始时间和结束时间这个时间区间表示基站服务该访问请求的时长，基站位置为基站的地理经纬度信息，用户ID为加密的用户编号，访问内容即通过基站请求的网络内容。为了方便，本文对基站的位置进行标签化处理，以基站的编号代表基站的位置，基站位置集合记为L={l1,l2,…,lN}。另外，对于众多的网络内容进行主题归类，主题类别集合记为T={t1,t2,…,tF}。

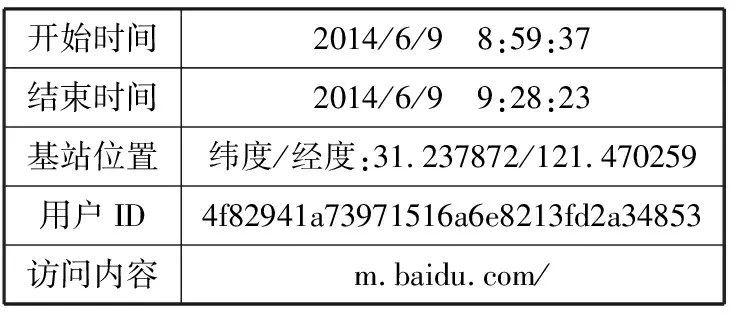
表1 移动网络使用详单数据

定义2用户-位置关系网络。根据UDR数据中的基站位置信息，用户与位置形成的偏好关系用网络表示为加权无向图P，记为P=(U,L,R)，其中，U表示用户集，L表示地理位置集，R表示图中关系边的权重关系集合，即R={rij|rij=(ui,lj),ui∈U,lj∈L}，其中rij表示用户ui对位置lj的偏好。统计一段时间区间内用户ui在每个基站的服务时长，作为该用户在各位置的滞留时长，滞留时长序列记为ηi=[ni1,ni2,…,niN]，其中ni1表示用户ui在位置l1的滞留时长，那么rij以ui在位置lj上的滞留时长占ui总滞留时长的比例表示：

(2)

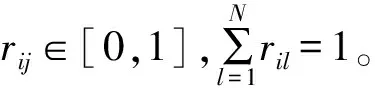
定义3用户-主题关系网络。用户通过基站访问内容的行为形成的关系网络可表示为加权无向图B，记为B=(U,T,W)，其中，U表示用户集，T表示内容主题集，W表示图中关系边的权重关系集合，即W={wij|wij=(ui,tj),ui∈U,tj∈T}，其中wij表示用户ui对主题tj的兴趣偏好。统计一段时间区间内用户ui访问的内容主题的频次，频次序列记为γi=[mi1,mi2,…,miF]，其中mi1表示用户ui访问主题为t1的内容的次数，那么wij以访问内容主题为tj的频次占ui总请求频次的比例表示为：

(3)

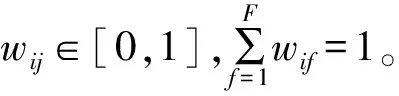
2.1.1 社交相似度网络

社交相似度指的是用户在社交拓扑上的连接紧密程度。在社交拓扑中若2个节点间连接数量越多且连接路径越短，则2个节点之间连接越紧密。基于以上原则，采用Katz算法[16]衡量社交相似度，不仅考虑2个节点之间的最短路径，还考虑2个节点之间的所有路径。同时，增加一个衰减因子α来控制不同长度的路径对2个节点之间相似度贡献值，具体如下:

(4)

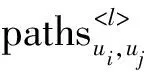
(5)

2.1.2 地理位置相似度网络

地理位置相似度指的是用户间在地理位置分布特征的相接近程度。利用余弦相似度表示为：

(6)

进一步地，地理位置相似度网络表示为：

(7)

2.1.3 主题相似度网络

主题相似度指的是用户间主题兴趣偏好的相接近程度。同样地，根据余弦相似度表示为：

(8)

进一步，主题相似度网络表示为：

(9)

2.2 BNMF-NF算法描述

对于上述多个相似网络的社区发现，本文提出的BNMF-NF算法首先通过加权网络融合的方式构建用户相似度网络：

V=(1-θ-ω)·Simsocial+θ·Simlocation+ω·Simtopic

(10)

其中，V表示融合后的相似网络，为了适应不同的场景加上θ和ω伸缩因子调整各部分的权重，例如当希望得到同一个校区的用户群体时，用户地理位置相似特征应占据较大的权重，当更希望得到具有相似主题兴趣的用户群体时，用户主题兴趣偏好的相似特征应占据较大的权重。对相似网络V进行非负矩阵分解，表示为：

(11)

其中，W为隶属度矩阵，其每行元素的值表示每个节点隶属于各社区的程度，k为预设社区个数。考虑在实际的社区结构中，网络中的节点通常不会同时属于多个社区[17]，因此对隶属度矩阵行向量施加l2范数约束以增强其稀疏性。同理，对H矩阵的列向量施加l1范数约束以增强其稀疏性。改进的有界非负矩阵分解如下：

(12)

其中，‖·‖F表示Frobenius范数，Wi,:和H:,j分别表示W的行向量和H的列向量，β和λ均为非负系数。目标函数(12)对于W和H整体而言是非凸的，使用交替最速下降法和迭代策略可求得其局部最优解，迭代更新式：

(13)

(14)

再对W(i+1)矩阵的各行进行归一化处理：

(15)

具体算法描述如下：

算法1BNMF-NF社区发现算法

输入：相似网络Simsocial、Simlocation和Simtopic，权重θ和ω，社区簇k，系数β和λ，误差ε

输出：隶属度矩阵W

1.通过公式(10)计算得到用户相似网络V

2.令i=1，随机非负初始化矩阵W(i)和H(i)，并由公式(15)归一化处理隶属度矩阵W(i)

3.REPEAT

4.通过公式(13)计算更新H(i+1)

5.通过公式(14)计算W(i+1)

6.由公式(15)归一化处理隶属度矩阵W(i+1)

7.ε(i+1)=|D(V‖WH)(i+1)-D(V‖WH)(i)|

8.i=i+1

9.UNTILi>imax或ε(i+1)≤ε

10.RETURNW(i)

3 实验与结果分析

3.1 数据集描述

本文选取中国电信运营商提供的某市匿名UDR数据集[18-22]，该数据集包含上万个用户，覆盖数千个基站，持续时间为一个月，以通信会话为基础，记录上万用户通过基站访问网络的行为。数据集的每个条目由匿名用户标识符、基站位置、会话时间、日期和月份组成。由于此匿名数据集缺少了用户社交关系等信息，另外选择Foursquare(NYC)数据集，该数据集包含了用户-用户社交关系和主题评论数据，并将这2个数据集通过映射组成新的实验数据集。由于数据集本身存在一些噪声数据以及访问稀疏的位置点，实验先对数据集进行过滤，将基站位置标签化并将主题进行分类，再筛选出请求数超过5条的用户及其拥有的社交关系。预处理完毕后，新的数据集包含2321个用户、2407个位置和378个主题。

3.2 对比算法与评价指标

为了验证本文提出的社区发现方法的有效性，选取如下算法进行对比实验：

1)Louvain：基于模块度优化的快速社区发现算法，只考虑用户节点的社交关系。

2)J-NMF: 程结晶等人[23]提出的一种联合矩阵分解的划分算法，在本实验中考虑用户社交关系和用户主题偏好关系进行联合矩阵分解。

3)BNMF-NF：本文提出的社区发现方法。

为了评价社区结构的划分质量，引入模块度Q值函数，定义为：

(16)

其中，V表示节点集合；M表示邻接矩阵；di和dj分别表示节点i和j的度；ci和cj分别表示节点i和j所处的社区，当i和j属同一社区时δ(ci,cj)=1，否则为0；m表示网络中边的总数。

除了衡量社区结构的划分质量外，主题兴趣的内聚性也是一种衡量社区划分内在特性的重要指标[24]，描述社区内所有用户的主题兴趣相似度定义如下：

(17)

其中，|EC|表示社区的边数，计算可知，当IC值越高时，社区的主题兴趣内聚性越好。

3.3 实验结果与分析

本实验主要关注算法在实验数据集覆盖位置中具有相似主题偏好的用户群体的划分效果，经多次选择并设置伸缩因子θ和ω均为0.4，使得位置偏好相似特征和主题偏好相似特征均占据更重要的角色。在社区结构特征评价上，比较了3种算法在实验数据上的实验结果。图1统计了不同社区规模下的用户数，Louvain算法只划分出13个社区，而J-NMF算法和BNMF-NF算法划分的社区数相当。

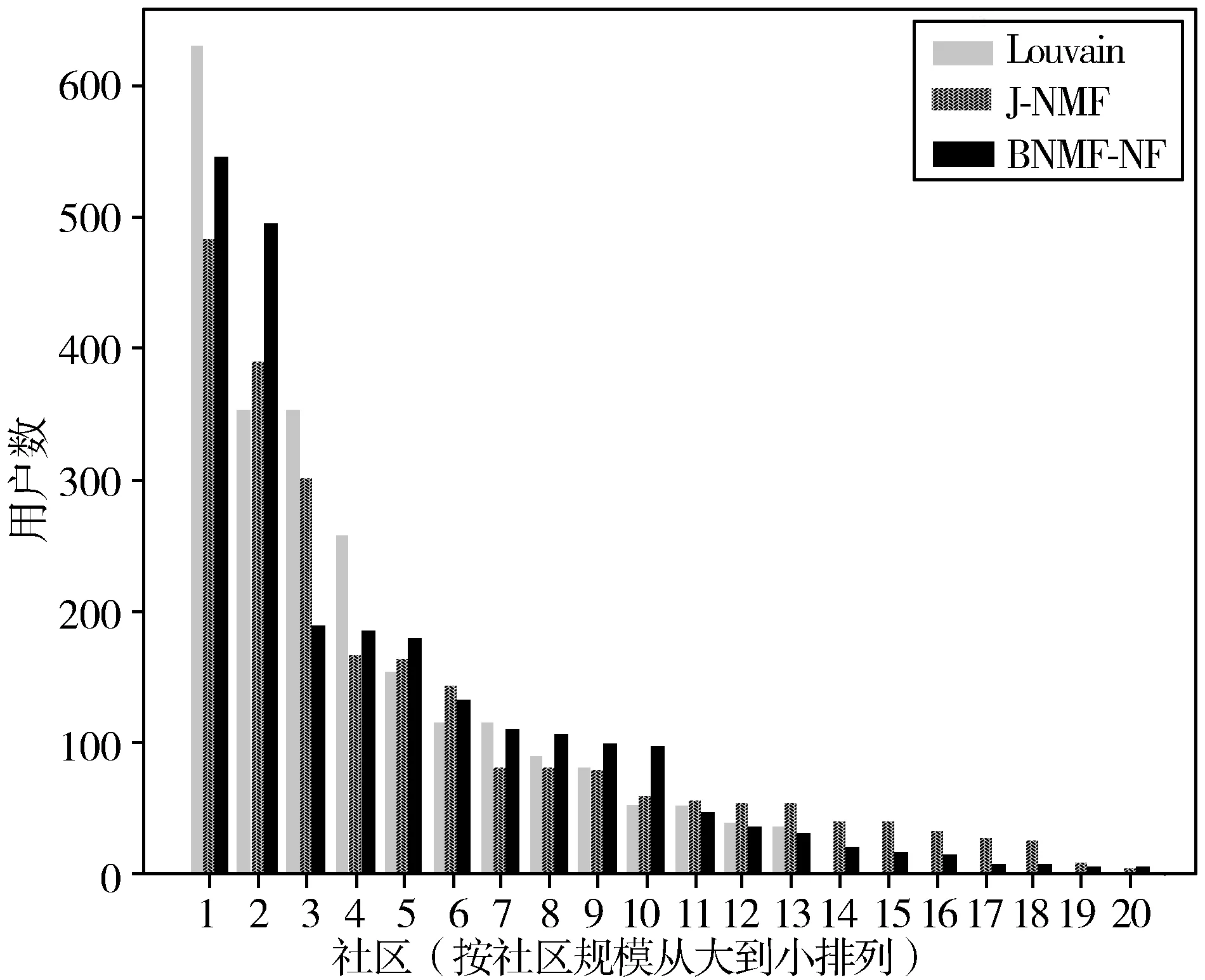
图1 不同社区规模下的用户数

表2给出了不同算法在多个社区簇参数下的模块度。

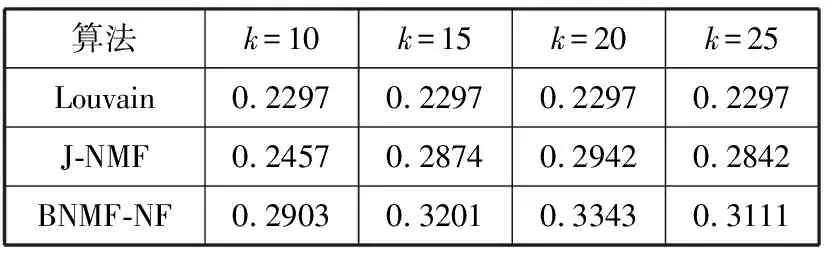
表2 3种算法在不同社区簇k参数下模块度对比

从表2可以看出，Louvain算法不受参数k的限制，根据式(16)所得到的Q值为0.2297，由于只考虑用户的社交关系，获得的模块度值均小于其他算法。另外，J-NMF算法和BNMF-NF算法模块度值都随着社区簇参数k的增大先增加再减小，在k=20时，模块度都达到最大值。比较实验结果发现，BNMF-NF算法相比J-NMF算法在不同社区簇参数下均能获得更高的Q值，故社区发现的效果更好。

为了评价社区内在的主题兴趣内聚性，本文比较了3种算法在数据集上获得的社区IC指标，结果如图2所示。不难看出，BNMF-NF算法所得到的主题兴趣相似度维持在0.4左右，高于其他算法。由于Louvain算法只考虑用户社交关系而导致社区主题兴趣内聚性较低。综上实验结果表明，本文提出的BNMF-NF算法所获得的社区不仅表现出紧密的外在结构特征，还能达到更好的主题兴趣内聚性。

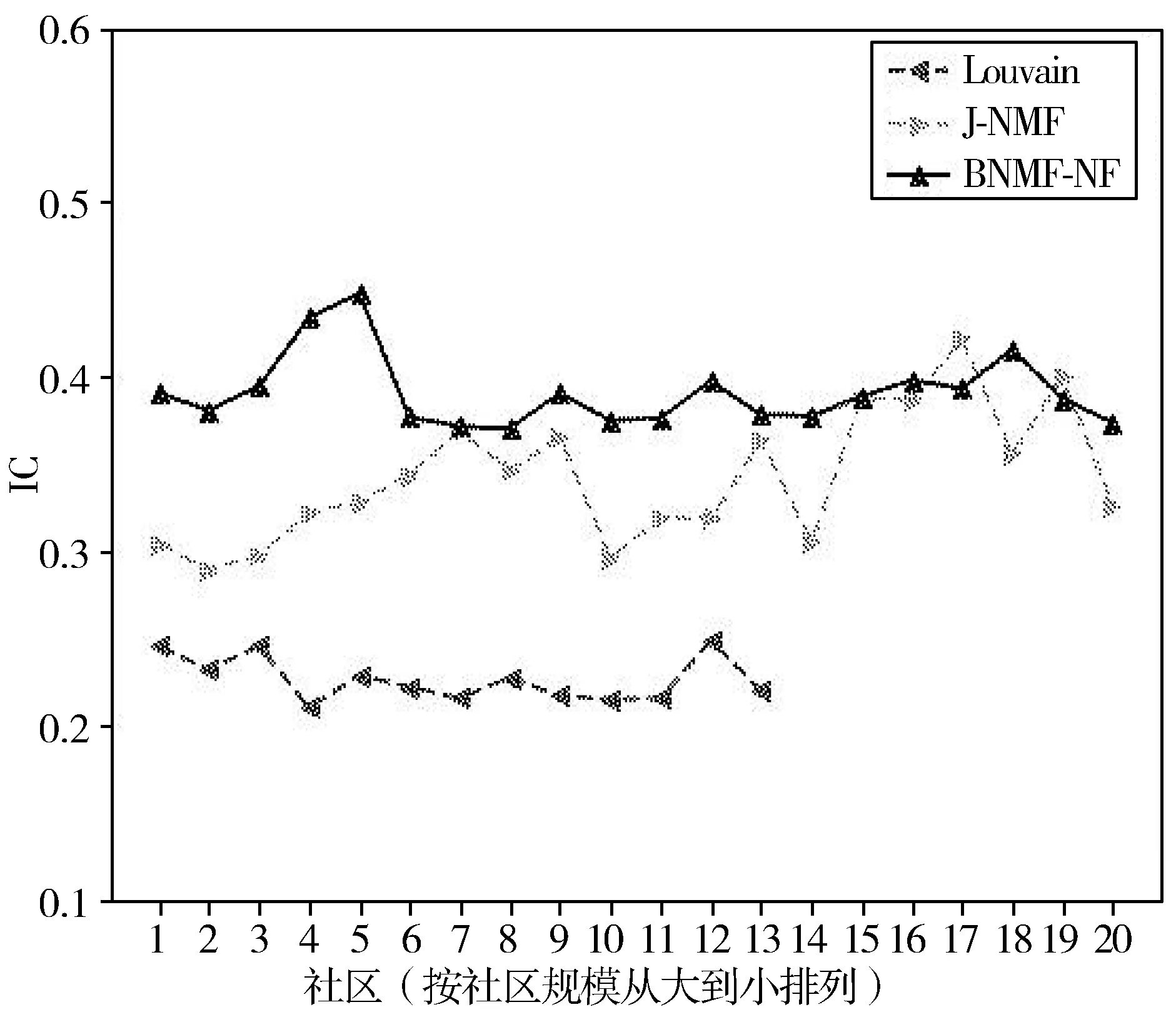
图2 社区主题兴趣内聚性

4 结束语

本文针对多维异质的移动网络提出了一种融合多维信息的社区发现方法BNMF-NF。具体地，从社交关系数据和移动网络使用详单数据出发，构建由移动用户、地理位置和内容主题等实体构成的异质网络模型，并利用网络融合的方法融合多维信息。改进了非负矩阵分解的稀疏性约束并采用交替最速下降法和迭代策略得到矩阵变量的迭代更新式，最终得到最优的社区划分结果。最后，实验结果表明，本文提出的BNMF-NF方法所获得的社区不仅表现出紧密的外在结构特征，还能达到更好的主题兴趣内聚性。

在未来的工作中，笔者将进一步优化网络融合过程，使得多网络融合能降低噪声，以后还考虑引入时间信息挖掘随时间而动态演化的社区结构。