基于高程归一化的布料模拟滤波算法

陈曦亮,王 雪,毕晓伟

(1.长安大学地质工程与测绘学院，陕西 西安 710064; 2.咸阳师范学院,陕西 咸阳 712000)

0 引 言

LiDAR(Light Detection and Ranging)技术是一种主动式的遥感技术，这一技术使用的是激光设备发出的脉冲信号照射到地面，记录每个脉冲信号从发出到打到地面点上返回所用的时间，利用时间和光速就可以计算出传感器设备到地面某点的距离，运用GPS全球定位系统和INS惯性导航系统确认激光发射中心的三维坐标和姿态倾角[1]。获得的点云数据有目标地面点的三维坐标信息，可以依次通过后续处理得到相关产品。这项技术具有可以全天候作业，可以获取常规摄影测量无法获取的困难地区的三维信息，作业周期短，生产费用相对较低，不需要昂贵的测图设备，在困难地区精度高于摄影测量的精度以及可以直接获取目标地物的DEM而不需要再次进行新的人工处理等优点[2]。

在对获取的点云数据进行处理的过程中，滤波的过程是相当关键的一步，如何找到一个最好的滤波方法是很多人研究的目的[3-4]。滤波方法有很多，具体可分为数学形态学滤波、TIN滤波、统计分析滤波、基于调整点云表面的滤波、分类与分割的滤波以及多尺度滤波等[5]，还有布料模拟滤波。每种方法都有其优缺点。基于分类和分割的方法比较适合城市地区，但对植被茂盛的地区有效性较低。TIN滤波的可靠性得到过很多证实，但对于地形不连续的区域滤波效果不太好[6]。统计分析滤波可以避免人为的参数调节，但稳定性较差。多尺度滤波借助多种策略对非地面点进行识别整合，对于平台地区效果较好，但对地形较复杂地区就不太适合。

2003年Zhang等[7]提出了一种渐进式的数学形态学滤波，该算法通过逐步迭代增大滤波窗口，并且根据坡度值动态变化高差阈值，但其地形自适应性较弱，设置高差阈值的时候也不能很好地顾及地形特点。2015年隋立春等[8]提出了一种改进的数学形态学滤波算法，提出了在“开”算子基础上增加一个带宽参数，提高了地形自适应性。2016年Zhang等[9]提出了通过计算机布料模拟的滤波算法。2018年，张昌赛等[10]对布料模拟的算法进行了适用性分析，给出了总结：布料模拟滤波算法具有效率高，在地形平坦地区精度也高，但在一些地形复杂的区域效果就欠缺一些。2020年，郑津津等[11]基于布料模拟滤波和随机森林进行了点云分类过程，并且提出了基于地面点进行高程归一化的思路。本文围绕这2种滤波算法来进行改进。利用这2类算法的特性来改进算法，使地面点和非地面点可以更高精度地分离，并适应多种地形。

1 数据预处理

在对点云数据进行滤波之前，需要对点云数据先进行一些预处理步骤，包括空间索引建立和一些粗差噪声点的剔除。

1.1 空间索引的建立

由于点云数据本身十分庞大，因此在数据处理前将数据本身进行一定的组织化是十分必要的步骤，本文采用空间格网索引结构来组织点云数据，本方法在2004年由Cho等[12]将其引入到 LiDAR 点云数据预先处理中。其基本原理是将离散点云所分布的区域用一个个大小相同的虚拟格网分开，每个格网就相当于点云的一个子空间容器，记录落入其中的点云子集。对于激光点云创建的虚拟格网如图1所示，其中，左图显示的是立体结构，黑点表示离散的三维激光点云各个点，灰色的立方体则表示所建立的其中之一的虚拟格网；右图则显示的是平面结构。白色小圆圈表示离散的激光脚点，正方形表示创建的虚拟格网。

图1 虚拟格网的空间索引

1.2 噪声点的剔除

点云数据中常见的粗差(噪声点)包括高位粗差和低位粗差，如图2所示，机载的LiDAR系统在飞行中受到了低空飞行物(如飞机、鸟类等)的影响，误将这些物体反射回来的信号当作了被测物体，高位粗差同时又叫做空中噪声点。低位粗差则是由于多路径因素影响又或者是激光测距仪自身的误差带来的极低点误差，低位粗差一般是低于实际地形的噪声粗差点，又称低点[13]。

去噪算法的原理：该算法对每个点的领域进行搜索，计算从一个区域点到周围相邻的区域点的距离，计算该区域点的平均距离和标准差，如果一个区域的距离平均值大于最大距离(最大距离=中值+标准差×标准差倍数)，则将该点视为噪声的点，通过选择适当的参数，如果某点和周围领域点的平均距离大于最大距离，可以将其视为粗差噪声点。消除在点云中的粗差[14]。

2 算法原理

2.1 渐进式数学形态学滤波

数学形态学理论用于LiDAR滤波的时候，有2种算子，即“开”算子和“闭”算子。“开”算子先进行腐蚀处理，再进行膨胀处理，“闭”算子则正好相反。本文使用开算子。腐蚀和膨胀操作如图3和图4所示。结构B为窗口模板[15]。

图3 腐蚀操作

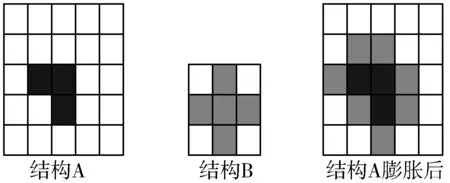
图4 膨胀操作

“开”算子的算法流程如下：

1)腐蚀处理。扫描搜索全部的LiDAR点云数据,以其中的一点为中心开一个W×W大小的窗口(搜索模板)，该窗口在整个的点云数据图像上进行逐行逐列的移动，这时记录各点的高程值并且进行比较，找到里面最小的那个值，使用这个最小的高程值代替扫描窗口中心点的高程值，直至所有点的高程都腐蚀完后才结束腐蚀步骤。

2)膨胀处理。再次扫描搜索所有的点云数据,使用和腐蚀操作同样大小的搜索窗口,并使该窗口进行逐行逐列的移动。此时,各个点的高程值均已被腐蚀操作时窗口内最小的高程值所代替,同样比较窗口各点高程值的大小，用窗口内高程值最大的值代替窗口中心点的高程值。继续循环该操作，直到所有点的高程值更新完毕。

3)地面点判定和提取。假设P点操作之前的高程值为Zp，dhT为要设置的阈值。开算子的操作结束后，对每一个激光脚点是否为地面点进行判断。其依据是：如果P点膨胀操作之后的高程值和其原始高程值Zp之差的绝对值小于或等于阈值dhT，则判定P点为地面点，若大于阈值就判定为非地面点[16]。

这里采用渐进式改变窗口大小的方法，其窗口大小随着迭代步长的增长而指数增长，关系式为Wk=2×pow(b,k)+1，其中，Wk为现窗口大小，b为设置的初始窗口大小，k为迭代次数。窗口大小增长到设定的最大窗口值为止。

利用研究区域的坡度值来进行高差阈值的计算。高差阈值dhT和坡度值s以及窗口大小Wk的关系如式(1)所示：

(1)

其中，C值表示单元格网的大小值。

2.2 布料模拟滤波

布料模拟滤波(Cloth Simulation Filtering, CSF)算法的过程可以看作是一种简单的模拟布料的物理过程。该算法假设在地表区域的正上方存在着一块虚拟布料，在重力的作用下该布料最终会覆盖在下方的地形表面上。假设这块虚拟布料足够柔软，则布料落下来的最终形状刚好便是对应下方区域点云的数字表面模型(DSM)。同理，如果把原始地形反向翻转过来，同时布料具有一定的硬度,则同样在重力作用下布料的最终形状就是点云的数字高程模型(DEM)[17]。布料模拟点云滤波算法的原理如图5所示。

图5 布料模拟滤波示意图

计算机里面所模拟的布料是由大量的离散节点构成的一个格网，格网中的节点相互联系并由连接线进行连接，同时假设各格网点均为具有恒定质量且无尺寸的质点，因此这种格网的方式也称作为质点弹簧模型[18]。要模拟布料在自由落体中某一时刻的形状，需要计算出各布料点的空间位置。假设各布料节点只在垂直方向进行移动，而且只受重力与邻近节点的相互作用力共2种力。当只考虑重力作用时，由牛顿第二定律可知，布料点的空间位置和其所受的作用力之间的关系可由式(2)确定：

X(t+△t)=2X(t)-X(t-△t)+G△t2/m

(2)

其中，m表示布料点的质量，G表示重力加速度常数，X(t)表示某一时刻的格网节点位置，△t表示时间步长。当时间步长和格网节点初始位置已知时，可以解算出格网节点的当前位置。

为了约束粒子在反转表面空白区域的反转问题，还需考虑粒子内部因素导致的位移 。任意选取2个相邻的粒子，如果2个粒子都是可移动的，则令二者往相反的方向移动同样的距离；如果一个是不可移动的，则移动另一个；如果两者具有相同的高度，则不进行移动[19]。位移量可以通过式(3)进行计算：

(3)

其中，d为粒子的位移量；当粒子可移动时，b等于1，不可移动时b为0；pi为p0的相邻粒子，n是点进行标准化到垂直方向上的单位向量(0，0，1)T。

布料模拟滤波算法的详细步骤如下：

1)上下翻转原始点云，对点云空间坐标进行转换。

2)设定格网分辨率，将原始点云进行虚拟格网化。把所有激光点与格网上的粒子在同一个水平面投影，找到每一个粒子的最邻近点，记录其投影前的高程。

3)对于每一个可移动的格网粒子，计算其受到重力影响产生的位移，并将该位置与其对应激光脚点的高程进行比较，若布料格网节点高程小于或等于激光脚点高程，则将该节点移动到激光脚点的位置，并标记为不可移动点。

4)计算各布料格网节点受邻近点作用力后需要移动的位移量。

5)重复步骤3和步骤4，当各节点的高程变化开始变得足够小的时候或者迭代次数达到最大，布料模拟过程就可以结束。

6)区分地面点与非地面点，如果LiDAR点与模拟粒子之间的距离小于预先设置的阈值，则认为其是地面点，反之则认为其为非地面点。

2.3 算法的改进

2.3.1 2种传统方法存在的问题

数学形态学算法的难点在于窗口大小的选取，窗口大小的参数决定了滤波的细节程度。窗口太大时，虽然基本能剔除大部分的建筑物等地物点，但是对一些地形复杂含有山地的陡峭地区时，容易将山顶信息剔除。窗口太小时，容易将一些尺寸较大的建筑物当成地面点保留。如图6所示。

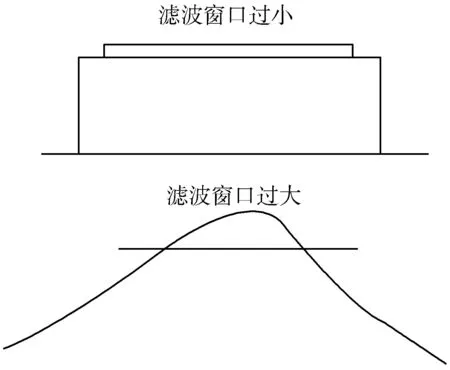
图6 建筑物和山地的窗口大小问题

除了窗口大小问题，还有高差阈值无法自动适应地形变化的原因，导致部分非地面点被识别为地面点而产生误差。比如，有坡度的区域由于高差阈值相应会增大，会导致斜坡上的房屋植被等非地面点被归类为地面点。

布料模拟滤波算法对于平坦地形地区的滤波效果十分良好，但是对于地形较为复杂的区域(如陡坡、山地等)或者低矮建筑物较多区域的效果不太好[20]。要么因为平地地区硬度参数设置过小或者迭代次数过多导致把一些低矮建筑物被算成了地面点，要么在陡坡山地地区因为硬度参数设置过大或者迭代次数过少导致山顶或者其他一些地形有变化区域的地面点被剔除，如图7所示。

图7 CSF算法易出现的2类错误

2.3.2 高程归一化

考虑到2种传统算法各自的缺陷，而布料模拟滤波算法最适应的地形为平坦地形，这种地形下能获得最好的滤波效果，能够保留大部分地面点的同时也能有效地过滤非地面点云。因此如何消除高程起伏带来的影响是关键，对点云数据进行一个归一化的操作，使得点云的高程值得到归一化，来消除崎岖地形带来的滤波精度影响。具体方法是先利用原始的点云数据粗分类的地面点生成DEM，利用DEM数据和原始点云数据进行归一化操作。

考虑到渐进形态学滤波在对地面点的正确分类方面的有效性，分离出的地面点点云大致反映了目标区域的地形变化特征，能够保留地形细节，因此采用渐进式数学形态学滤波所分离出来的地面点构建不规则三角网，选取点云格网中的最低点为种子点，和最邻近的2个点构建初始三角形，随后，各顶点分别寻找最邻近的一个点组成不规则三角网(TIN)表面，在三角网中提取栅格格网的值，在三角网中，格网落到三角形顶点时，直接获得三角形顶点的高度值，如果不在顶点，则该点的高度值通过线性插值方法获得，在三角形边的2个顶点上的采用2个顶点的高程内插，在三角形中的则采用各顶点高程内插[21]。

生成的DEM数据为TIF格式，将其和原始的点云数据结合进行高程归一化，通过每个点云所处的格网位置找到对应的DEM格网处，点云数据的原始高程值和粗DEM对应格网处的高程值的差值就是归一化的高程值。归一化之后要保存原始的点云高程值，用于滤波完之后的反归一化。然后对归一化之后的点云使用布料模拟滤波，具体的步骤在前面关于布料模拟滤波方法的介绍中已经给出，按照原有的步骤进行迭代循环，分离出地面点和非地面点，滤波结束后赋予原有高程值进行反归一化，得到结果。技术路线如图8所示。

图8 本文技术路线

3 实验结果及分析

实验所用的数据来自ISPRS官方网站的标准数据，选取samp51、samp12、samp52这3块区域，均为已经经过人工编辑分类好的标准数据，进行滤波前已经进行过粗差剔除，可以直接进行结果分析，一共选择了3组数据。实验采取C++/PCL+CloudCompare软件的编译方式进行，运行环境为Windows10系统。3个区域数据的基本情况如表1所示。

表1 研究区域点云基本信息

3．1 实验结果

samp51数据处理过程如图9所示，其中的内容从左到右、从上到下包括原始的标准点云数据、由渐进形态学滤波结果生成的DEM栅格数据、高程归一化处理后的点云以及最终的滤波结果。而本文方法相比渐进形态学和普通布料模拟滤波结果的比对如图10所示，可以看出，本文方法结果使得渐进形态学滤波中因高差阈值的不确定性或者窗口大小问题而未被剔除的部分非地面点被剔除，同时因普通布料模拟滤波而被错误剔除的一些有地形起伏变化的斜坡或者陡峭山地地面点云也得到保留，同理其他2个样本samp21和samp52的处理结果也类似，samp12结果和比对分别如图11、图12所示，samp52结果和比对分别如图13、图14所示。

图9 samp51的滤波处理过程

图10 samp51和本文算法的比对结果(左形态学，右布料模拟滤波)

图11 samp12的滤波处理过程

图12 samp12和本文算法的比对结果(左布料，右形态学)

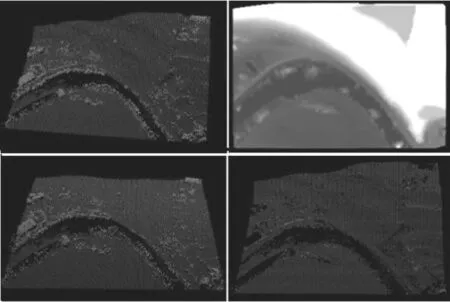
图13 samp52的滤波处理过程

图14 samp52和本文算法的比对结果(左布料，右形态学)

3．2 定量分析

为了验证算法的精度和可靠性，需要对最终的滤波结果进行一个定量分析。在定量分析中，把误差分为2类：Ⅰ类误差和Ⅱ类误差。Ⅰ类误差定义是地面点识别为非地面点的误差，也称作为拒真误差，Ⅱ类误差是非地面点识别为地面点的误差，也称作为拒伪误差。如表2所示，e和f分别表示标准数据中的地面点和非地面点的个数；n为数据点的总个数，而3种误差的计算公式如下[22]：

(4)

(5)

(6)

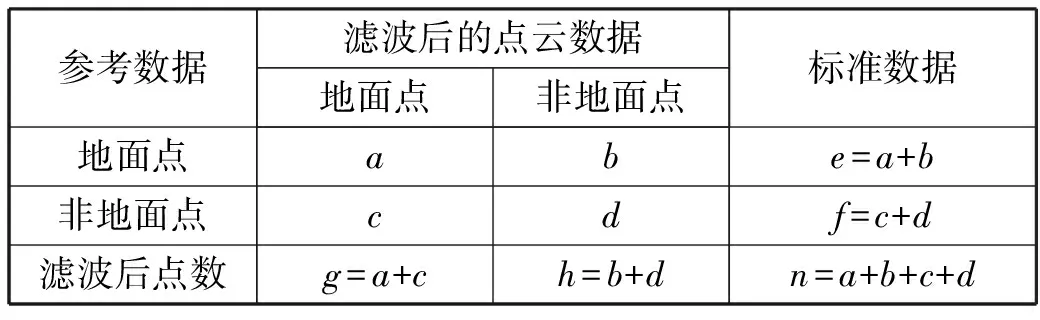
表2 滤波误差定义

将滤波结果和标准数据进行比对，本文实验所选取的参数在同一样本下都一致，根据点云密度范围确定格网大小，渐进形态学滤波的参数如下：坡度值根据地形变化选取，最小距离阈值为0.5 m，最大距离阈值为3 m，最大窗口值为10 m。布料模拟滤波的参数如下：距离阈值为0.4 m～0.5 m，迭代次数为500次，DEM格网大小为2 m或1.5 m。最后得到的结果经过计算后各样本各方法的结果如表3所示。

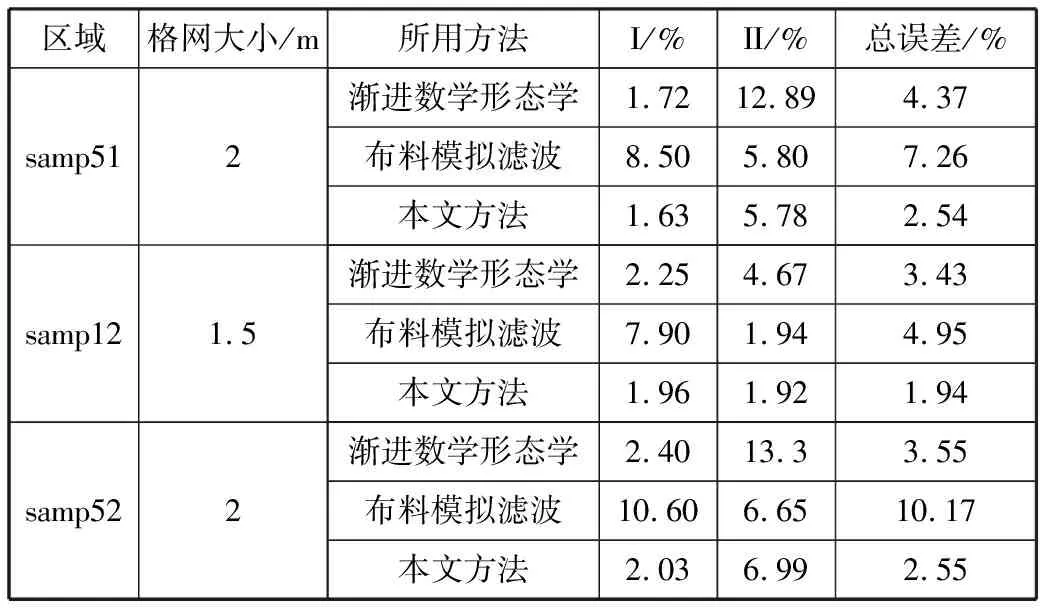
表3 各区域滤波实验误差统计结果

由表3结果可知，本文方法在进行高程归一化处理之后的点云再进行布料模拟滤波后结果均比传统的渐进形态学滤波和布料模拟滤波要好，相比渐进形态学滤波，在保证了Ⅰ类误差稳定的同时，降低了Ⅱ类误差，相比布料模拟滤波，在保证了Ⅱ类误差稳定的同时，降低了Ⅰ类误差。同时，总误差也均有降低。

将本文方法和近2年的其他相关改进算法作对比，只选择其他文中有关本文的3个研究区域的结果。选取了2020年周钦坤等[23]、2018年陈斐然等[24]改进的数学形态学滤波算法、2019年王逸超等[25]一种改进的多级曲面滤波，其结果如表4所示。

表4 滤波结果误差比较

结果表明，虽然本文算法个别的I类误差和II类误差可能相较其他方法更高，但总体而言，总误差都比其他几类方法低。

4 结束语

本文对原始点云数据进行了一个高程归一化的操作，解决了传统的布料模拟滤波和渐进形态学各自存在的一些问题，同时对滤波结果进行了对比验证，结果及分析表明：

1)对高程归一化之后的点云数据再进行布料模拟滤波，在地形复杂崎岖的地方有非常不错的效果，优于传统的渐进形态学滤波和布料模拟滤波，也优于部分其他的改进算法。

(2)本文方法依赖于生成的DEM精度，因此在处理之前进行点云粗差剔除是必不可少的步骤，本文采用了渐进形态学滤波作为获取DEM的前处理过程，也可以尝试其他算法比如渐进三角网加密。

3)本文需要人工设置DEM格网大小，步骤之间的自动化方面还有待加强。