改进线性平行黏结模型的宏细观参数关联性研究

李汪洋， 石 崇， 张一平， 陈闻潇， 张 坤

（河海大学岩土力学与堤坝工程教育部重点实验室/岩土工程科学研究所，南京 210098）

近年来，基于离散单元法研究岩石与岩体非连续性质成为岩土类数值分析的热点方向. PFC3D是当前应用最广的颗粒流离散元程序工具，其中线性平行黏结模型经常用来模拟岩石性质，在岩石损伤［1］、围岩稳定性［2］、节理岩体破坏机制［3-5］等方面已经诸多应用，但该模型在建立宏观参数与细观参数联系时非常困难，导致宏观试验与数值试验曲线难以吻合.

国内外学者针对土石混合体和岩石等材料，已经尝试了多种方法来确定细观参数和其宏观力学性质间定性或定量关系. Nardin 等［6］定性地研究了黏性材料细观参数及其宏观特性之间的关系. Potyondy 和Cundall［7］系统总结了平行黏结模型在Lac du Bonnet花岗岩隧道工程模拟中的应用，并给出了模型细观参数的选取方法. 刘良军等［8］基于研究线性平行黏结接触模型中的细观参数与单轴压缩试验应力-应变曲线及试样破坏形式的对应关系，将细观参数分为4类. 刘富有等［9］选择Flatjoint接触模型作为岩石模拟的基本模型，用单轴压缩和巴西劈裂数值试验测试岩石宏观参数，对数值试验进行正交设计，采用多因素方差分析和回归分析研究宏观和细观参数之间的关系. 刘相如等［10］基于平直节理接触模型，研究了接触面单元数N、平直节理模量Ec、平直节理刚度比kr、摩擦系数μ、平直节理抗拉强度σc、平直节理黏聚力c 和平直节理内摩擦角θ 7种细观参数对岩石宏观力学参数的影响.

通常采用PFC方法模拟岩石等高黏结材料的单轴抗拉强度都相对较高，导致单轴抗压强度和单轴抗拉强度比值（UCS UTS）为3～4. 而实际很多岩石的UCS UTS 常常超过10［11］，甚至达到20～30. 目前，多采用抑制颗粒旋转的簇平行黏结模型［12］来提高UCS UTS 值，但单轴抗压强度受簇中颗粒数影响较大. 本研究改进了常规平行黏结模型，建立了由13个参数控制的数值模型开展正交试验，分析了岩石宏细观参数间的定性与定量关系，建立了一种快速达到压拉比等宏观参数的标定方法.

1 线性平行黏结细观模型

1.1 常用的线性平行黏结模型

在采用数值方法研究岩石工程的破坏机理，尤其是模拟岩石材料时，线性平行黏结模型［7］使用最为广泛.

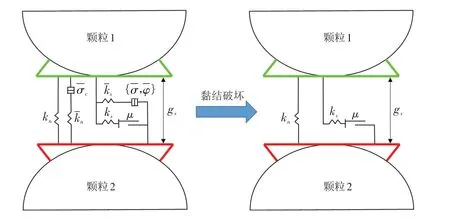
图1 线性平行黏结模型组成结构Fig.1 Microstructure of linear parallel bond model

线性平行黏结模型更新接触力和接触力矩的力-位移法则如下：

1.2 考虑细观特征分布的颗粒体系改进模型

基于线性平行黏结模型所计算得出的单轴抗拉强度往往较高，导致单轴抗压强度和单轴抗拉强度之比UCS UTS 为3～4［14］，无法满足很多岩石实际需求（UCS UTS 常常超过10）的客观限制. 出于提升压拉比的需求［15］，对线性平行黏结模型进行改进，将模型产生的ball-ball接触以不同填充基质配比随机分为强接触和弱接触两组［16］（图2）. 不同接触组的参数设置见表1. 表1中RE表示弱接触组黏结有效模量与强接触组值的比值，Rk表示黏结法切向刚度比与线性法切向刚度比的比值，Rσ表示弱接触组抗拉强度和黏聚力与强接触组值的比值.

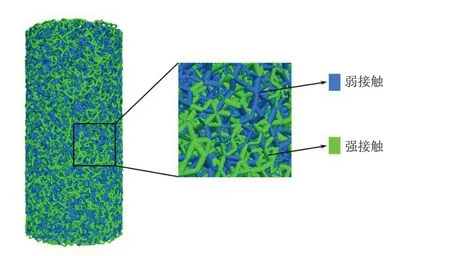
图2 模型强弱接触随机分布Fig.2 Random distribution of strong and weak contacts in the model

表1 模型不同接触组参数Tab.1 Parameters of different contact groups in the model

自然界中的岩石作为一种破坏程度不同的物质，Weibull 分布已被用来描述岩土材料的累积损伤［17-18］.它有两个优点：数值都为正，并且在距离尺度参数几个标准差范围之外的数值的概率接近于0，特别是在形状参数较大的情况下. 岩土材料的强度参数均为正，同一矿物在岩土材料中的强度参数略有差异. 本节采用Weibull分布来表示矿物间内部胶结强度的随机分布，威布尔分布的概率密度函数如下：

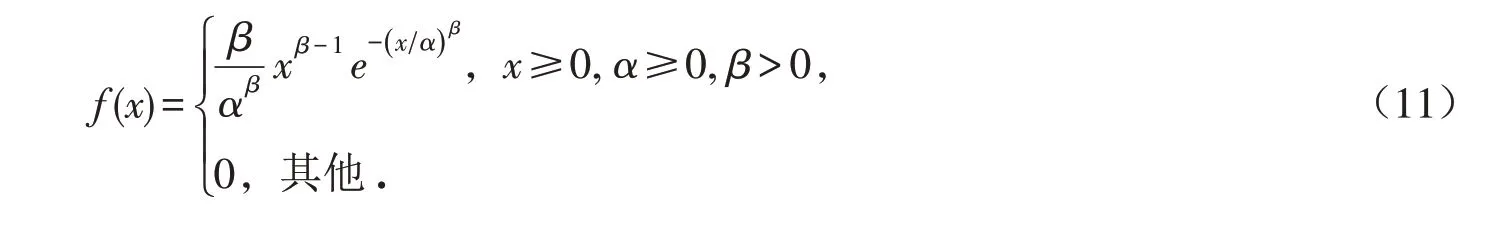
式中：α 和β 分别为控制概率密度函数均值和峰值的尺度和形状参数. 威布尔分布的概率分布函数见下式：

蒙特卡洛方法是一种以概率统计理论为指导的数值计算方法. 通过蒙特卡洛方法构造（0，1）区间上均匀分布的随机数f，然后生成一个服从威布尔分布的随机变量X. X的表达式如下：

因此改进模型由13个参数构成：黏结有效模量Eˉ*、线性有效模量/黏结有效模量E*Eˉ*、黏结法切向刚度比kˉ*、抗拉强度σˉc、黏聚力/抗拉强度cˉσˉc、摩擦系数μ、摩擦角φˉ、力矩分配系数βˉ、填料比例Rf、Weibull分布参数β、强度比例Rσ、模量比例RE和刚度比比例Rk. 其中Rf表示ball-ball 接触分组中弱接触组接触数与总接触数的比值，抗拉强度、黏聚力和黏结有效模量按表1赋值后再乘以Weibull分布的随机变量X，以实现离散效果，Weibull分布中参数α 设为1.0. 图3为不同β 取值下X的概率密度函数，可见随着β 的增大，X取值越来越集中于1附近.

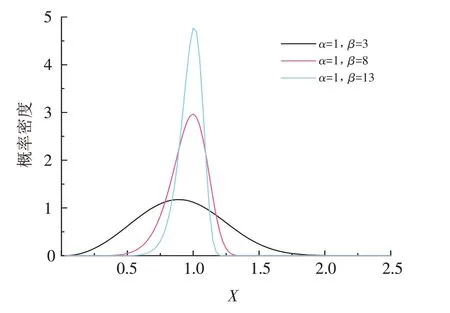
图3 不同参数值下变量X 的概率密度函数Fig.3 Probability density function of variable X for different parameter values

2 正交试验数值模拟

2.1 正交试验原理

正交试验设计是建立在概率论、数量统计和实践经验的基础上，寻求因素水平较优组合的一种简单、高效、快速的试验设计方法［13］. 在正交试验设计中，各因素的水平根据先验知识进行确定，然后进行全部因素水平的组合，再从所有试验点中依据正交性选择部分有代表性试验点来实施试验，选岀的这部分试验点构成一张正交表.

2.2 宏观和细观试验参数

根据室内常规三轴试验曲线，选取弹性模量E、泊松比ν、单轴抗压强度UCS、单轴抗拉强度UTS、内摩擦角φ、黏聚力c、裂纹损伤应力σcd作为试验的宏观参数. 考虑到对岩石高压拉比的要求，采用宏观参数单轴抗压与抗拉强度之比UCS UTS 来代替单轴抗拉强度UTS .

岩石体积应变压缩膨胀的拐点被称为裂纹损伤应力σcd，当应力超过σcd后，即使应力保持不变，也会有越来越多的微裂纹贯通导致岩石破坏，因此裂纹损伤应力σcd可以作为岩石的长期强度［19-20］. σcd对于单轴抗压强度UCS 来说是一个相对值，本文定义裂纹损伤应力水平指标σcdUCS 作为试验的宏观参数.

宏观和细观参数选取如表2. 如果能建立细观参数与宏观参数间的内在规律，无疑可以大大简化参数标定过程消耗的时间.

2.3 PFC3D数值试验

采用PFC3D数值方法进行压缩和拉伸数值研究，三维数值模型如图4. 试样为圆柱体，半径25 mm，高度100 mm，四周和上下施加墙体进行固定. 试样颗粒共23 719个，最大粒径1.5 mm，最小粒径0.5 mm，孔隙率0.35.

表2 线性平行黏结模型宏细观参数Tab.2 Macroscopic and microscopic parameters of linear parallel bond model

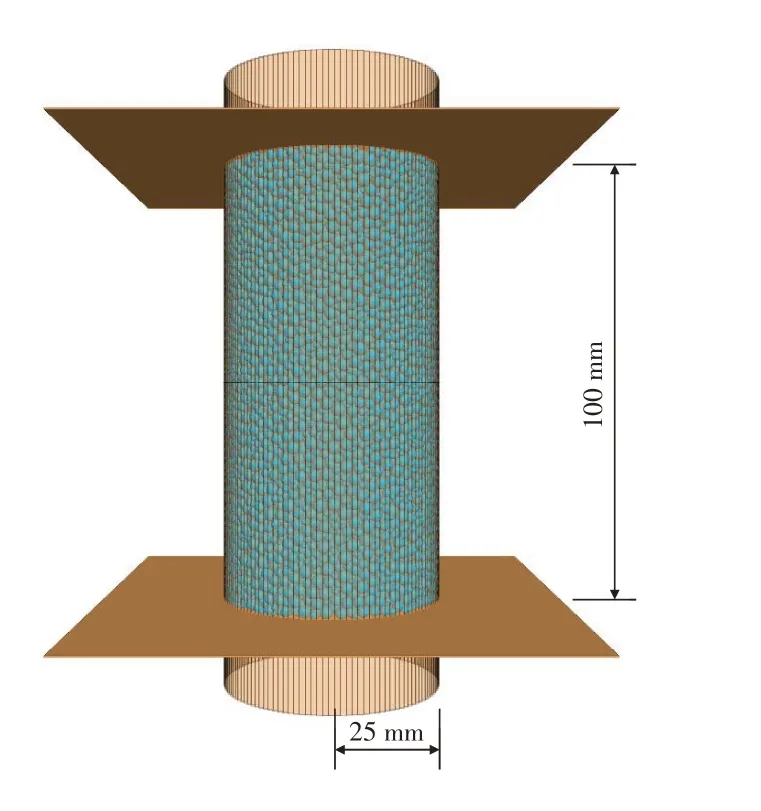
图4 三维数值模型Fig.4 Three-dimensional numerical model

对模型进行单轴压缩和单轴拉伸数值试验，应力-应变曲线如图5a和b所示. 图5c和d为单轴压缩的体积应变和泊松比与轴向应变的关系曲线. 根据结果曲线确定宏观参数单轴抗压强度UCS 和单轴抗拉强度UTS，弹性模量E 取轴向应变0.05%和0.15%间的割线斜率，见式（14）；泊松比ν 取轴向应变0.1%和0.2%对应值的平均，见式（15）；裂纹损伤应力σcd取体积压缩膨胀转化点对应的轴向应力. 最后进行三轴压缩试验，根据莫尔圆确定黏聚力c 和内摩擦角φ .

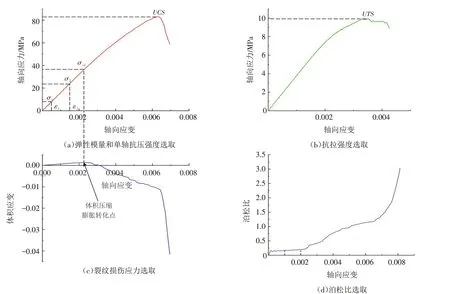
图5 宏观参数确定Fig.5 Determination of macroscopic parameters

2.4 正交试验设计

选取表2中的13个细观参数作为正交试验研究因素，每个因素选取3个水平，各因素的因素水平见表3，7个宏观参数作为参数标定的指标. 选择正交表L27313安排数值试验（表4）.

表3 因素水平表Tab.3 Factor level table

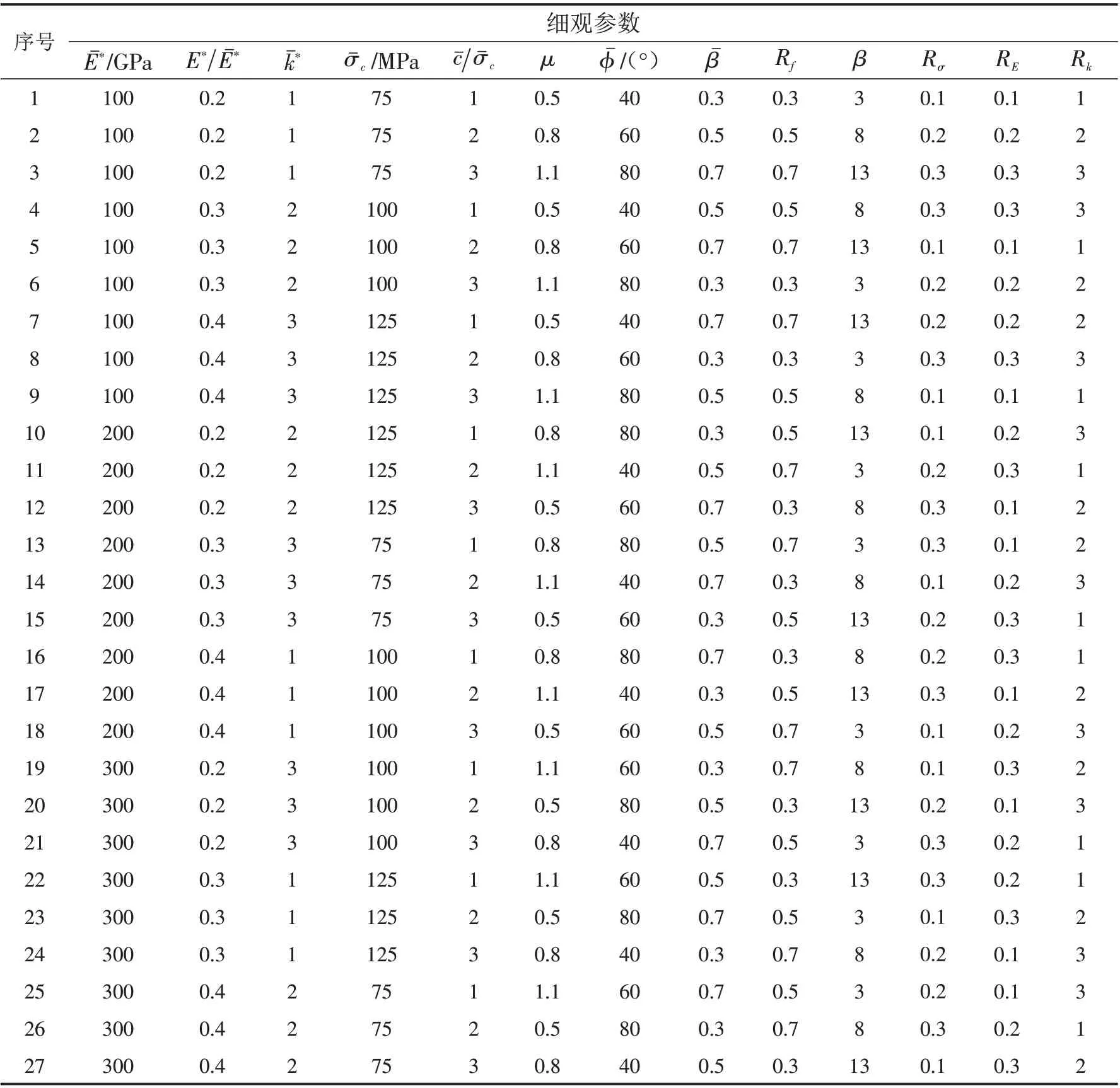
表4 正交数值试验方案Tab.4 Orthogonal numerical test scheme

3 正交试验结果分析

按照表4进行PFC3D单轴压缩、单轴拉伸及三轴压缩（围压1 MPa）的数值试验，得到试验结果（表5）.宏观参数中压拉比UCS UTS 范围为3～19，可以很好地满足实际岩石的要求.

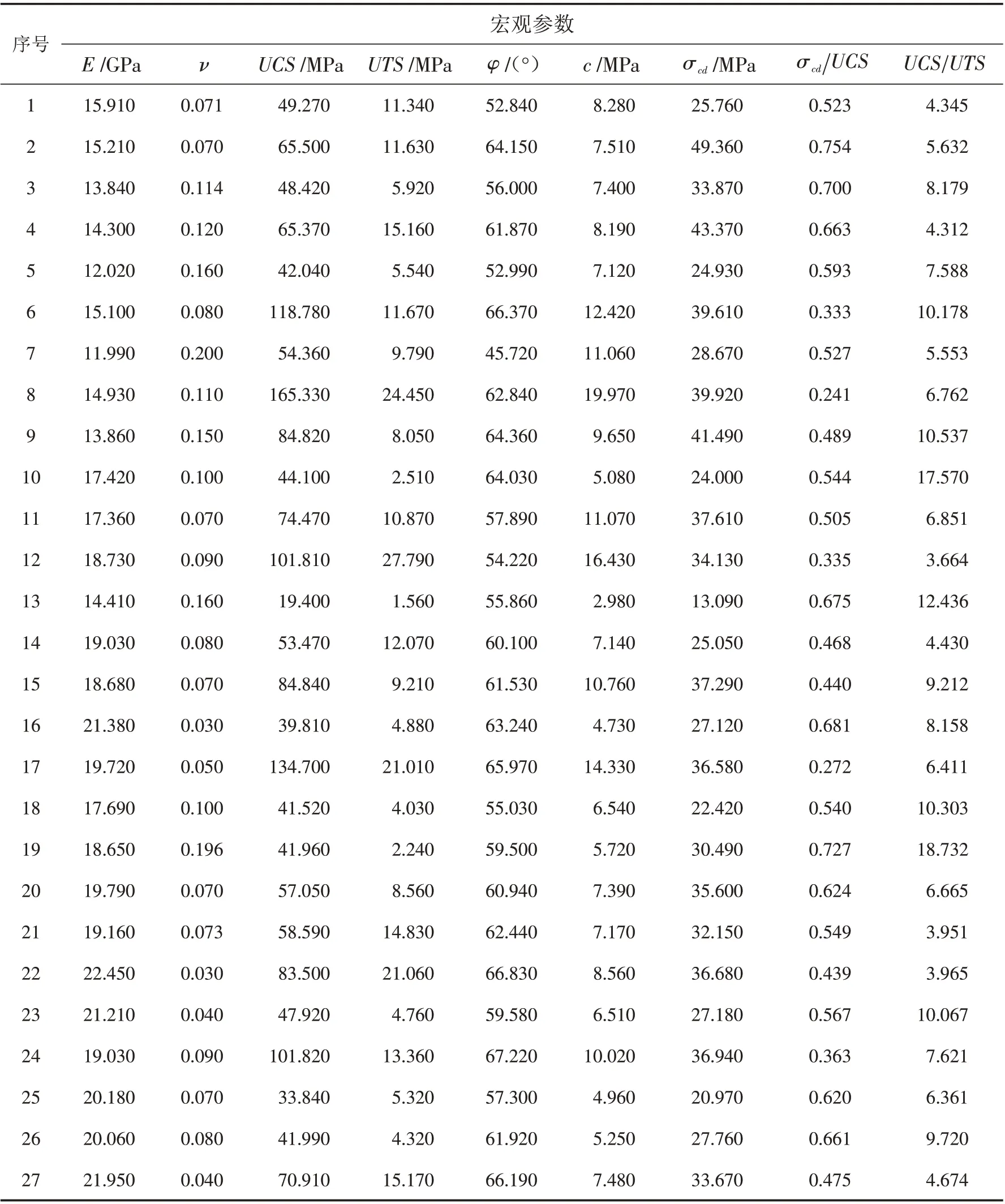
表5 正交数值试验结果Tab.5 Orthogonal numerical test results

3.1 各因素相关性分析

采用皮尔逊积矩相关系数计算各细观参数和宏观参数之间的相关性，如式（16），计算结果见表6.

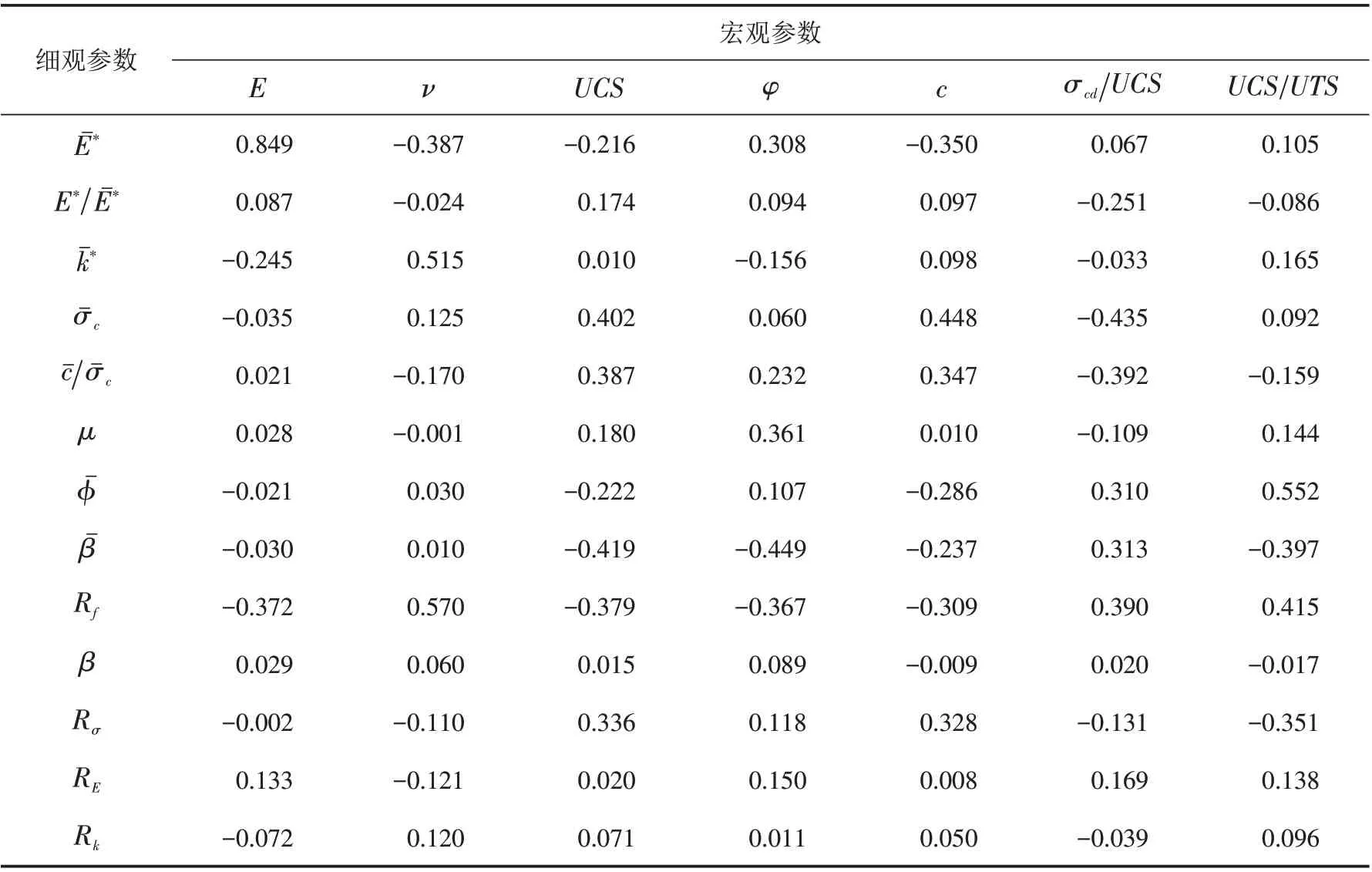
表6 皮尔逊积矩相关系数Tab.6 Pearson product-moment correlation coefficient

3.2 多元回归分析

根据图6可以得到各宏观参数的主要影响因素，分析如下：

根据上述分析，用岩石宏观参数的主要细观影响因素对其进行多元线性回归分析，拟合公式见式（17）～（23）.

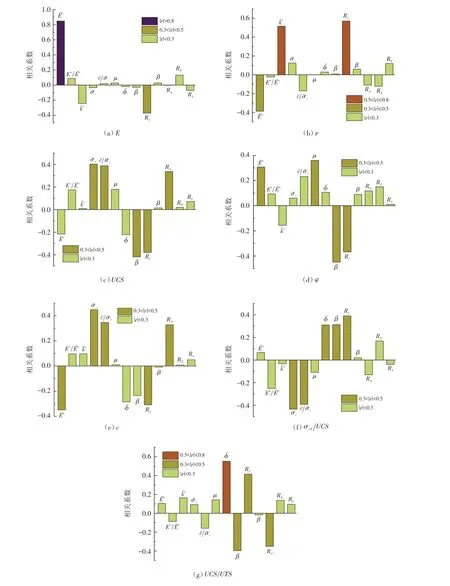
图6 各宏观参数对应相关系数Fig.6 Correlation coefficients corresponding to each macroscopic parameter

从上述拟合公式可以看出，除式（20）外，其他公式的R2大于0.7，拟合效果较好，说明宏细观参数间的线性关系比较明显；式（20）的R2较小，拟合效果一般，说明宏细观参数间关系复杂，不能简单地用线性关系来描述，需进一步分析.

图7为宏观参数φ 与对应各细观参数的试验平均值的关系曲线，散点表示试验值，点线表示各组宏观参数试验结果的平均值，椭圆表示置信度为95的置信区间.

从图7可以看出，μ 和Rf与内摩擦角φ 呈现出一定的对数关系，对其进行非线性曲线拟合，再结合其他变量进行拟合后的结果如式（24）.

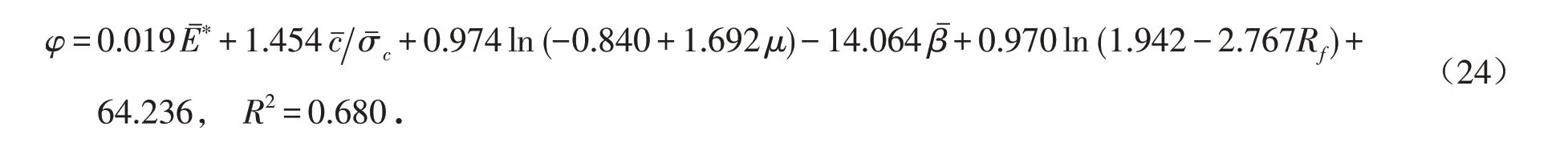
综上，经过修正后的宏细观参数间的拟合公式见式（25）～（31），E 单位为GPa，UCS、c 单位为MPa，φ 单位为（°）：

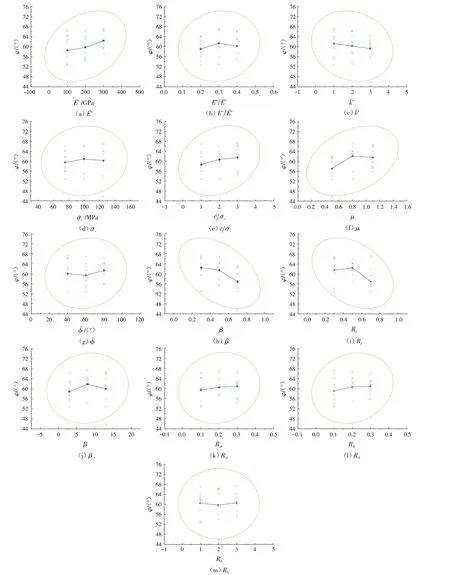
图7 宏观参数φ 与各细观参数试验平均值关系曲线Fig.7 Curves between macroscopic parameter φ and mean values of test results of each microscopic parameter

4 细观参数快速标定实例

依据文献［21］对灰砂岩常规三轴压缩试验结果得到的宏观力学参数进行模型细观参数标定，UCS UTS值取为12.

基本标定步骤如下：

3）进行PFC初步数值模拟，通过单轴压缩、单轴拉伸以及三轴压缩试验得到宏观参数. 根据初步模拟值和试验值的差值以及宏细观参数间的趋势关系调整细观参数，减小误差，最终达到理想效果. 细观参数最终取值见表7.

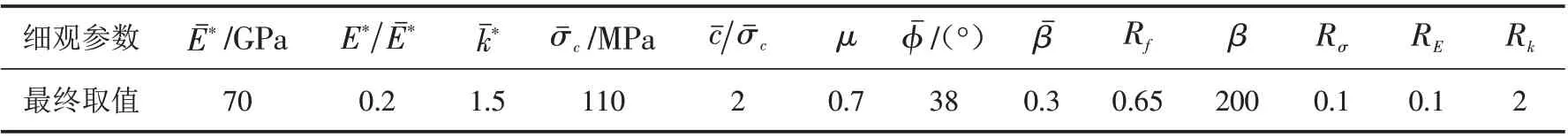
表7 灰砂岩模型细观参数最终取值Tab.7 Calibration values of microscopic parameters of grey sandstone model

数值模拟与室内物理试验得到的宏观参数对比如表8，误差除σcdUCS 外均在7%以内，表明快速标定方法是可行的.

图8为单轴压缩情况下，数值模拟与室内物理试验得到的应力-应变曲线，模拟结果与室内试验结果基本相符.

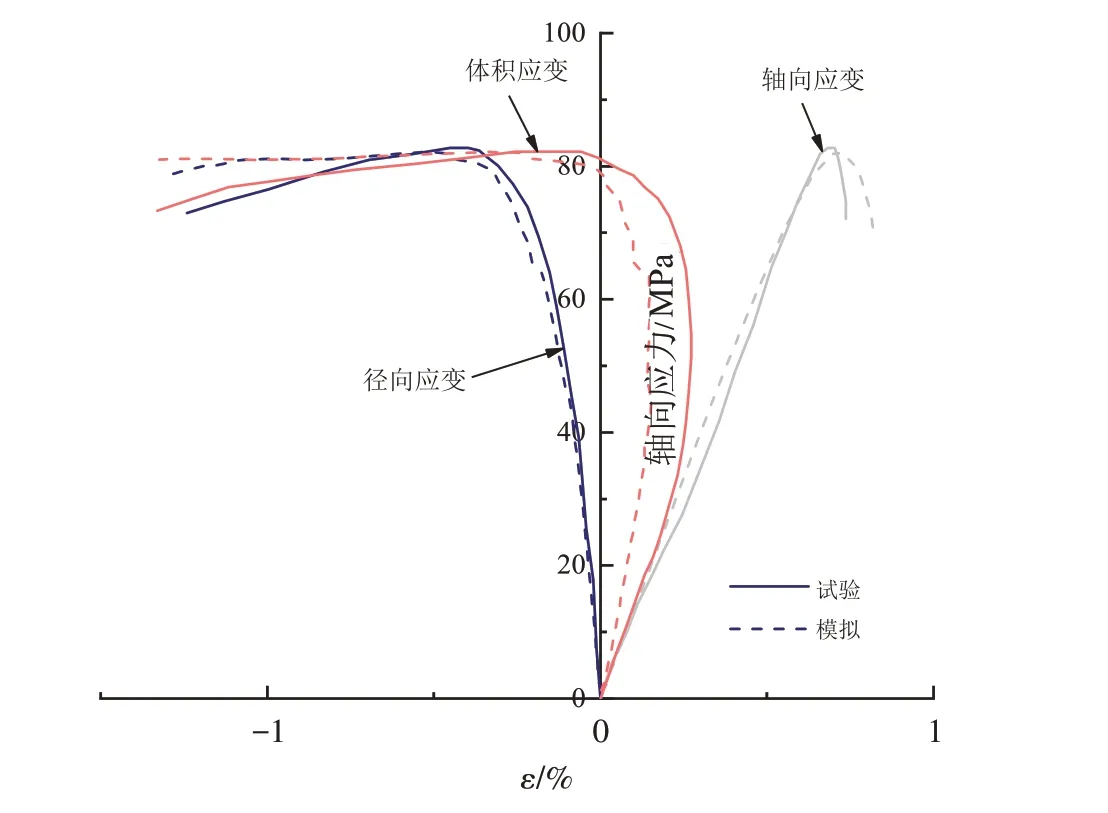
图8 单轴压缩应力应变曲线Fig.8 Stress-strain curves under uniaxial compression

5 结论

以改进的线性平行黏结模型作为颗粒接触本构模型，对PFC3D模型进行正交数值试验，研究了线性平行黏结模型13个细观参数与岩石7个宏观参数间的关系，并探讨了PFC3D线性平行黏结模型细观参数的标定方法，得出以下主要结论：

1）通过对线性平行黏结模型的改进措施，可以有效提高数值模拟结果的压拉比UCS UTS，满足实际工程中岩石的需要.

2）关联性研究表明，宏观参数与模型细观参数关系较复杂，个别参量无主导因素. 此时可先假定一部分参数取值，如E*Eˉ*、kˉ*、βˉ、Rf等，再利用标定出的规律确定主要细观参数，可以大大简化标定过程.

3）利用所得出宏观、细观参数之间的关系，依据灰砂岩的室内物理试验结果对线性平行黏结模型的细观参数进行颗粒流标定，模拟结果与室内试验结果基本相符，表明可用该方法标定岩石力学参数.