双主梁钢板组合梁截面剪力滞效应研究
邵真宝 ,王佐才 ,2
(1.合肥工业大学土木与水利工程学院,安徽 合肥 230009;2.安徽省土木工程防灾减灾工程技术研究中心,安徽 合肥 230009)
1 引言
在中小跨径桥梁中,双主梁式新型钢板组合桥梁的技术经济优势逐渐显露,在桥梁工程建设中的应用越来越多。然而,作为一种新型桥梁截面形式,用传统规范对其进行设计计算难以保证计算精度,新截面形式表现出的相关力学性能还有待深入研究。根据以往研究经验,钢板组合梁桥受弯时,翼缘板内纵向正应力并不一定会如初等梁假定一样沿翼缘板宽度方向均匀分布,在一定条件下反而会表现出明显的剪力滞后效应,即受弯翼缘板内纵向正应力在截面横向呈不均匀分布。考虑到双主梁钢板组合梁的结构形式,混凝土桥面板与两个工字钢梁连接,主梁间距较大,与单个主梁的钢—混凝土组合梁相比,应力不均匀分布的情况将会更加显著,因此非常有必要研究其剪力滞效应。
对于剪力滞效应的求解,可以采用能量法和最小势能原理,根据变分法原理推导出组合梁基本微分方程,进一步代入一定边界条件和相应的荷载工况,即可求解出组合梁截面各点的应力闭合解。
固镇至蚌埠高速公路工程九湾浍河特大桥引桥部分即为钢板组合梁桥,引桥采用分幅布置,单幅采用两片主梁,即为本文所述双主梁钢板组合梁截面形式,选取为本文研究对象。
2 双主梁钢板组合梁截面翼缘板纵向正应力解析解
本文的研究对象为双主梁钢板组合梁,横截面构造见图1所示。引入直角坐标系,将组合梁截面形心设为坐标原点,将组合梁纵向桥跨方向设定为坐标轴方向,将组合梁截面竖向设定为坐标轴方向,坐标平面与梁的对称平面重合。

图1 双主梁钢板组合梁截面图
2.1 基本假定
①钢材和混凝土材质均匀,各向同性且本文只研究材料处于弹性受力阶段的情形。
②假定组合梁在对称竖向荷载作用下,组合梁中和轴位置确定方法仍按照初等梁理论来计算。
③组合梁承受荷载,钢梁腹板的剪切变形对受力的影响忽略不计。
④假定钢梁与混凝土板的竖向位移一致,即挠度相同。
⑤假定组合梁混凝土板和钢梁是完全刚性连接,不考虑二者之间纵向的相对滑移,即忽略截面滑移效应。
⑥假定混凝土板只考虑纵向正应变和剪切变形,竖向应变、横向应变和板平面外剪切变形均很小,可以忽略不计。
2.2 控制微分方程的建立
变分法分析剪力滞效应的首先要选定合适的剪力滞翘曲位移函数。以便能够准确描述剪力滞后的影响。国内外学者尝试过多种函数形式,通过改变不同剪力滞翘曲位移函数形式进行推导理论公式研究截面剪力滞效应,对比发现,采用二次函数形式描述混凝土板纵向位移模式已足够精确。有学者提出,在选定截面剪力滞翘曲位移函数时,需要考虑截面轴力自平衡的问题,同时文献[11]也表明,对抛物线型翘曲位移函数进行考虑轴力平衡的修正与否,对剪力滞效应计算精度的影响并不大,本文采用文献[11]的结论,不予考虑。
根据上述原因,本文选取的混凝土板纵向翘曲位移函数形式为二次抛物线,以梁的挠度,混凝土板的纵向位差函数为未知数,表示混凝土板的纵向位移,假定混凝土顶板纵向位移为、混凝土悬臂板的纵向位移为。
具体如式(1)
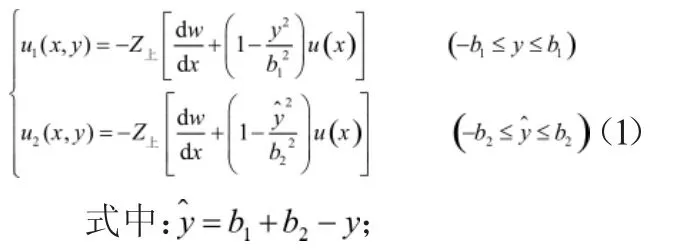
u(x)——混凝土板的纵向位移差函数;
b——混凝土板顶板宽度的一半;
b——混凝土板悬臂板宽度。
根据最小势能原理,在外力作用下,结构处于平衡状态。当有任何虚位移时,体系总势能的一阶变分为零,即
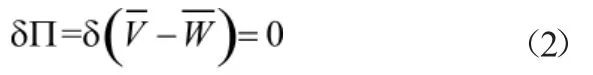
式中:


各项势能的计算如下:

式中:
w——组合梁的竖向挠曲位移。
体系形变势能包括

式中:


E——混凝土弹性模量;
G——混凝土剪切模量;
t——混凝土板厚度;
ε——混凝土板主梁内侧的混凝土板纵向正应变;
ε——混凝土板主梁外侧的混凝土悬臂板纵向正应变;
γ——混凝土板主梁内侧的混凝土板纵向剪切应变;
γ——混凝土板主梁外侧的混凝土板纵向剪切应变。
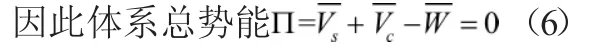
由应变位移关系有
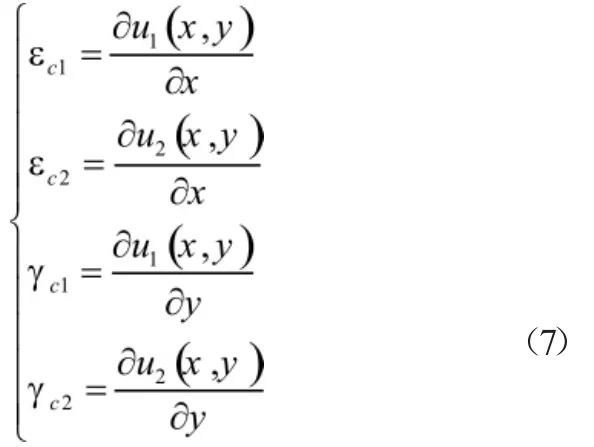
将式(1)代入式(7)中得到
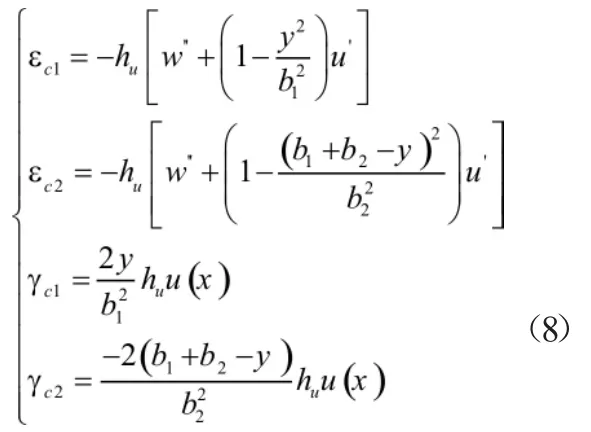
将式(8)代入式(5)中得到

式中:
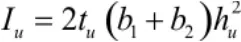

I——钢梁对组合梁换算截面形心轴的惯性矩。
将式(3)、(4)、(9)代入式(6)中得到
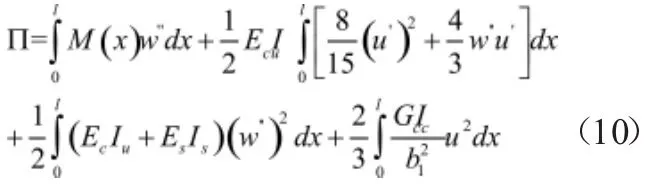
将(10)求变分,得到下列微分方程:

对上式整理得

并令其等于零,即δΠ=0,得到下列微分方程及边界条件:

整理式(13)并令
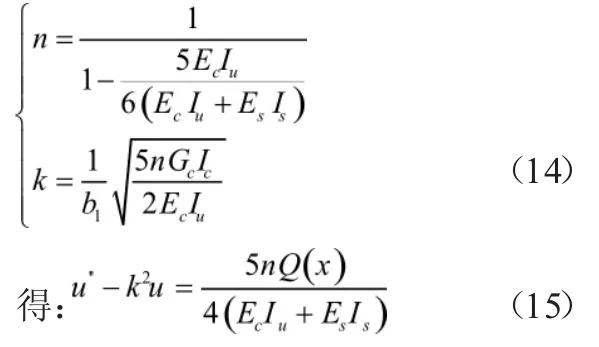
方程一般解的形式为

其中特解u*仅与剪力Q(x)的分布有关,系数C与C可以由组合梁代入具体的边界条件确定。
式(16)即为双主梁钢板组合梁剪力滞效应的控制微分方程。因此,考虑剪力滞效应影响的混凝土板弯曲正应力:

根据一定的边界条件,按控制微分方程解得 u(x),代入式(17)即可得到应力解析解。
3 特定边界条件下
3.1 简支梁在集中荷载作用下解析解,如图2所示

图2 简支梁承受集中荷载
在 0≤x≤a时

在时
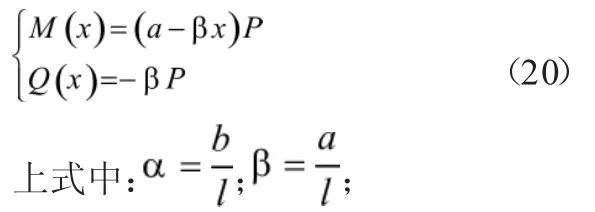
在0≤x≤a时,将式(19)代入式(16)得到混凝土板纵向位移差函数的控制微分方程为:

在a≤x≤l时,将式(20)代入式(16)得到混凝土板纵向位移差函数的控制微分方程为:
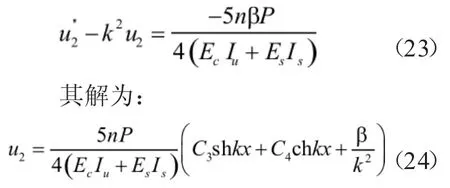

连续条件:x=a,u=u
x=a点上,变分中的边界条件为:

根据上述边界条件及连续条件,得:

解上面连续方程得到:

将式(27)代入式(22)和式(24),可以求得:

从而有简支组合梁在集中荷载作用下应力解析解:

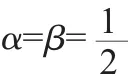

3.2 简支梁在均布荷载作用下解析解,如图3所示
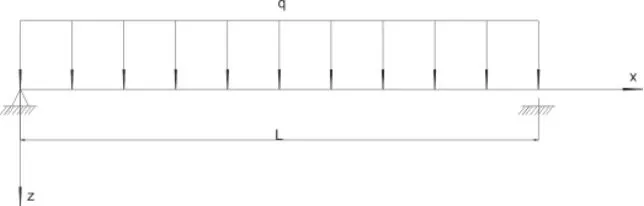
图3 简支梁承受均布荷载
弯矩与剪力方程为:

将式(34)代入式(16)得到混凝土板纵向位移差函数的控制微分方程为:
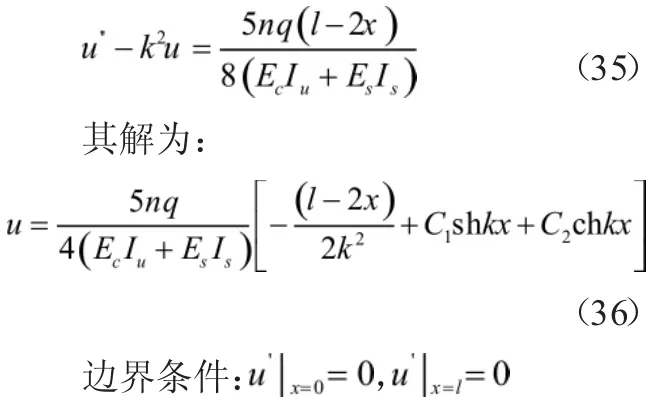
根据上述边界条件得:

将式(37)代入式(36)得:
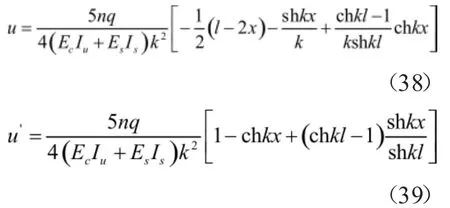
从而有简支组合梁在均布荷载作用下应力解析解:

简支组合梁跨中截面正应力为:

4 算例分析
算例采用简支边界,为双主梁钢板组合梁简支梁,计算跨径为,组合梁具体截面尺寸,如图4所示,桥面板采用弹性模量为的C50混凝土材料,钢梁为弹性模量为的Q345D钢。混凝土主梁内侧混凝土板宽度的一半,悬臂板宽度。运用本文前面推导的理论公式,计算出混凝土桥面板截面形心轴上各点应力值。

图4 算例组合梁的1/2横断面图/mm
采用大型通用有限元软件ANSYS建立算例双主梁钢板组合梁桥的有限元分析模型。本文钢板组合梁桥面板材料为混凝土,采用ANSYS中实体单元SOLID65单元模拟,主梁钢材为Q345D,采用ANSYS中shell181单元模拟。建立算例的ANSYS有限元分析模型,如图5所示。对算例进行计算分析,得到在相应荷载工况下混凝土桥面板纵向应力。
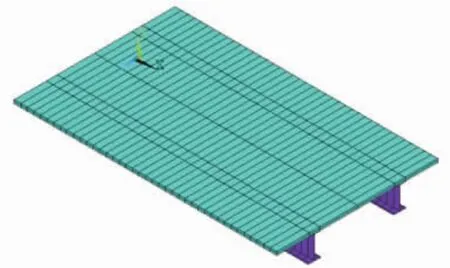
图5 双主梁钢板组合梁桥有限元模型
根据所得混凝土桥面板各点正应力值,可以作图得到混凝土桥面板正应力横向分布图,用合力大小不变的原则,可以据此得到一个应力平均值,根据剪力滞系数的定义,用横截面各点的实际应力除以该值,所得计算结果即可作为各点的剪力滞系数来描述组合梁截面的剪力滞后效应。
算例组合梁在跨中集中荷载作用下,分别通过建立有限元模型计算分析和运用本文推导所得公式计算下得出的混凝土桥面板剪力滞系数,如图6所示。算例组合梁在均布荷载作用下,在有限元和本文公式计算下得出的混凝土桥面板剪力滞系数,如图7所示。

图6 集中荷载作用下双主梁钢板组合梁剪力滞系数比较图

图7 均布荷载作用下双主梁钢板组合梁剪力滞系数比较图
从图6、图7可以看出,本文公式计算所得解析解与有限元分析结果吻合较好,有效验证了本文所得理论公式的精度和适用性。
对双主梁钢板组合梁,图6、图7说明主梁位置处存在显著正剪力滞效应,考虑剪力滞影响很有必要。
5 结论
①本文推导了双主梁钢板组合梁简支梁在均布和集中荷载作用下,弹性阶段的应力解析解,通过算例得到相应的剪力滞系数。
②与有限元法分析结果相比,按本文分析得到的结果吻合良好,用变分法分析双主梁钢板组合梁的剪力滞是可靠的。
③对于双主梁钢板组合梁简支梁桥,混凝土桥面板内存在显著的剪力滞效应,其影响不应忽略。

