受天气与交通事故影响的安全路线选择模型

章诗琪，魏斐斐，范馨月

贵州大学 数学与统计学院，贵阳550000

随着云计算、大数据和物联网等技术的发展，城市交通领域提出了“智慧交通”的概念，国内各大城市都由“智能交通”建设向“智慧交通”建设转变。简单来说“智慧交通”系统就是能够提示用户什么时间该做什么事。车辆导航就是智慧交通的一种重要体现，用户只需要输入起点和终点，系统就会给你规划较优出行路线，驾驶员所需要做的就是听着导航提示安全驾驶。

目前导航路线的选取方法主要是基于距离最短或时间最短两种，导航为了降低计算复杂度，忽略了车辆在行驶过程中，路线上交通状态的变化情况，导致所提供的路线并不一定是最优路线。行程越长，实际行程时间与参考时间的误差越大。

交通系统是典型的不确定系统，一方面，如恶劣天气、交通事故等能够导致交通网络供给侧的不确定性，从而影响交通网络通行能力退化；另一方面，如特殊事件、时间因素等会导致交通网络需求侧的不确定性[1]。交通供给和需求侧的波动性会导致路段的出行时间在一定范围内随机变化，而且这种变化会显著影响出行者出发时间和路径选择。

传统意义上最短路径问题的定义是在给定的OD（Origin-Destination）中，找到一条具有最少通行时间或者花费的路径。这类问题已经引起了多个领域（如交通运输、交通通信等）专家和学者的关注，并对其进行了广泛研究。由于交通流量、天气的变化，以及交通事故发生的概率等不确定因素，都会使通行情况发生很大的变化。交通状况受到很多不确定因素的影响，如交通事故、信号灯失灵以及天气变化等。对这些不确定的影响因素的探究过少，会使得当前路径规划对于行驶状况的预估存在较大误差。

当前较为常用的求解最优路径法有EBSP*算法[2]、精英蚁群算法[3]、Dijkstra算法[4]、A～*算法改进[5]、平行四边形限制最短路径算法[6]等。它们在空间复杂度、时间复杂度、易实现性及应用范围等方面各具特色[7]。但是最佳路径分析作为交通网络分析中最基本最关键的问题，它不仅仅是一般地理意义上的距离最短，还需要保障以“人”为主观的安全因素，因此针对当前时间最优或路径最优的路线研究模型忽略了最重要的“安全”问题，这类单因素路径研究最优选择模型相对而言就比较过时了。

针对上述原因，利用近几年的贵阳市交通事故情况、天气影响因素，综合考虑道路安全路径规划。为保障国家和人民生命财产安全，确保公路畅通，预防事故的发生，需要在原有导航中完善安全因素选择影响，给出行者提供更加合理安全的出行路线。

如图1所示，本文将对天气数据和交通事故数据进行预处理，根据处理结果选出有代表性的区域和路段，对其建立模型，用泊松分布模型去计算每个交通事故易发点发生交通事故的概率，再用加权方法和马尔可夫模型计算每条道路不发生交通事故的概率作为安全系数，最后将计算结果进行对比，为出行者提供决策。

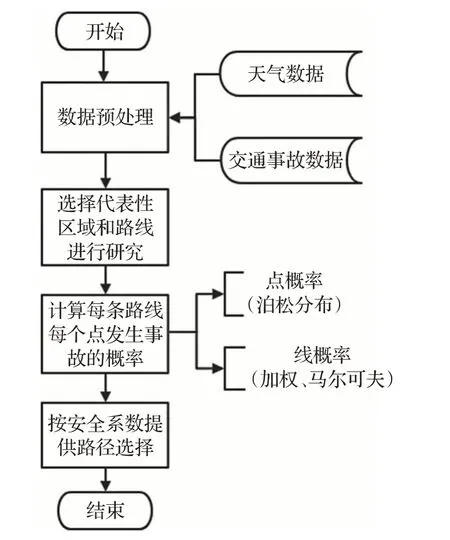
图1 工作流程图

1 数据来源

数据来源于贵阳市交通管理局事故鉴定中心2017年8月至2018年4月的交通事故数据以及贵阳市政府数据开放平台贵阳市天气数据。

贵阳市交通事故数据包含了交通事故发生地点、发生时间、事故车辆、事故描述等信息，由于每发生一起交通事故，就会产生一条数据，数据较多，故对交通事故数据按事故发生点进行统计，结果发现贵阳市观山湖区交通事故的分布较为均匀，故选取观山湖区作为研究对象，并按事故频数整理出发生交通事故较多的地点作为事故易发点。贵阳市天气数据包含2017 年8 月至2018年4月每天的天气类型、地点、气温等信息，由于气象局的天气数据不能精确到小时，故只对日数据进行研究。

贵阳市位于东经106°27'，北纬26°44'，海拔高度在1 100 m左右，常年受西风带控制，属于亚热带湿润温和型气候，2017年8月到2018年4月贵阳市的雨天和阴天占比较重。而雨天道路路面湿滑，会增加交通事故的发生几率。尽管雪天也会增加交通事故的发生几率，但贵阳市雪天较少，数据不足以支撑，因此仅对晴天、阴天及雨天进行研究，但本研究可以对其他地区进行推广。将天气数据与事故数据进行汇总之后得到的结果如表1所示，得到10个事故点9个月内的交通事故在不同天气下的发生频数，可以看出阴天和雨天发生的频率较高。

表1 贵阳市观山湖区交通事故频数表

2 道路交通事故发生概率计算方法

2.1 泊松分布

由于单位时间内出现的事件流服从泊松分布，单位时间内一段路上发生的交通事故数近似服从泊松分布，交通事故的发生数量X 是随机的，则其概率密度函数为[8]：

式中，k=0,1,2,…，λ 为泊松分布的参数，λ ＞0。由于参数λ 未知，而求解方法通常基于经典的参数估计，但需要大样本的支持，且不容易满足条件。

事实上，许多待估计的参数并不是完全未知，人们可以根据过去的经验了解一些关于这些参数的信息。贝叶斯方法将观测数据与从以往经验中推断出的一些间接信息相结合，弥补了样本量小的缺陷，在样本量小的情况下做出了更合理的参数估计。

贝叶斯方法[9]将待估计的参数本身视为随机变量，因此从经验中可以推断出该参数也服从一定的分布，称为先验分布。在获得样本之后，总体分布、样本与先验分布通过贝叶斯公式结合起来得到一个关于未知量λ的新分布，称为后验分布。任何关于λ 的统计推断都应该基于λ 的后验分布进行。因此可以利用贝叶斯估计来得到λ 的估计值，进而计算出每个交通事故点发生交通事故的概率[10]。

泊松分布参数λ 的先验分布常取为Gamma 分布，其密度函数为：

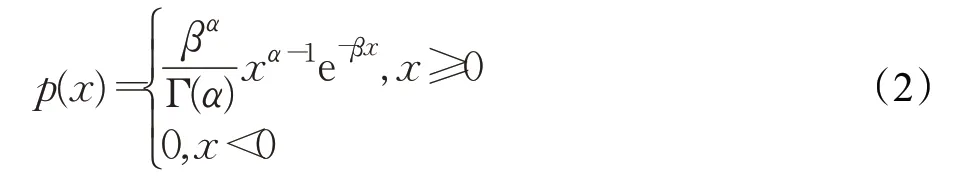
X 与λ 的联合分布为：

其中，k=0,1,2,…,λ ＞0。于是边际分布为：

其中，k=0,1,2,…,λ ＞0,α ＞0,β ＞0。式（4）是负二项分布，可以把整个路径上9个月的事故总数在各事故地点中的分布看作是该负二项分布的一个样本。由于负二项分布的均值为E(k)=α+α/β,方差为Var(k)=α(β+1)/β2,如果用样本均值和样本方差分别代替E(k)和Var(k)，仍记作E(k)和Var(k)，故用矩估计法对α 和β 估计量为：

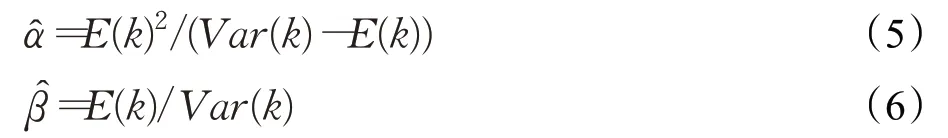
由贝叶斯估计的共轭分布特性，泊松分布参数λ 的后验分布仍为Gamma 分布。取后验分布的均值作为泊松分布参数λ 的估计量，则λ 贝叶斯估计为：

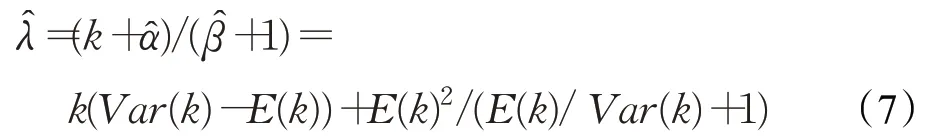
2.2 马尔可夫模型

将每个事故点看作X ，设{Xn,n ∈N+}为一随机序列，时间参数集N+={0,1,2,…}，其状态空间S={a1,a2,…,aN}，若对所有的n ∈N+，有

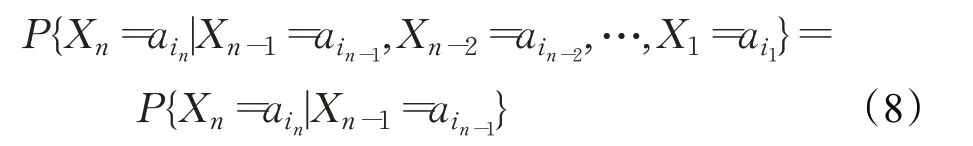
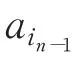
在实际问题中，时常需要知道系统的转移情况，故引入转移概率[12]：

其中i,j ∈S。式（9）中的转移概率pij(m,n)表示已知在时刻m 系统处于状态ai，或说Xm取值ai的条件下，经n-m 步后转移到状态aj的概率。也可以是在已知系统在m 时刻处于状态i 的条件下，在时刻n 系统处于状态j 的条件概率。

转移概率具有如下的性质：

由式（9）可知转移概率是一个条件概率，故式（10）是显然的。又由于

对于马尔可夫链，其k 步转移概率满足下面的切普曼-科尔莫戈罗夫方程：

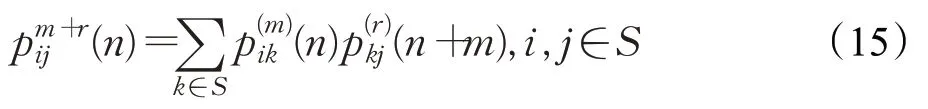
也即在开始状态i，经过m+r 步转移到j 状态，必须要从i 状态先经过m 步到达状态k，在经过剩下的r 步到达状态j。

3 安全系数计算的模型构建

3.1 事故点发生交通事故的概率

对2017 年8 月至2018 年4 月的交通事故数据进行假设检验[13]，检验其是否服从泊松分布，原假设为该数据服从泊松分布，备择假设为该数据不服从泊松分布。通过检验得到结果，p 值为1，若给定显著性水平α=0.05，p 值远远大于0.05，故而接受原假设，认为所需数据是服从泊松分布的。针对观测窗口内的所有实验数据即每个地点发生交通事故数服从泊松分布，可以从所有实验数据中选择一块分布均匀的实验区域数据进行细致建模。

针对所有实验数据，选择分布均匀的观山湖区数据进行观测，在导航软件中输入白云区行政中心和北京西路，如图2所示自动获得3条路径，找出3条路线中所经过的交通事故易发点，共10个点：第一条路线为白云区白云南路—白云区白金大道—观山湖区长岭北路—观山湖区长岭南路—观山湖区金阳医院—观山湖区龙泉苑街；第二条路线为白云区白云南路—白云区白金大道—观山湖区会展城—观山湖阳关大道—观山湖区世纪城；第三条路线为白云区白云南路—白云区白金大道—观山湖区长岭北路-观山湖区阳关大道。

图2 导航路线图

利用整条路线上每个月发生的事故数得到样本均值为27.875，样本方差为138.563，带入泊松分布的模型中，得到概率p=0.082。根据此法，得到3 条路径上所有事故发生点在单位时间内发生车祸的概率，但同一地点在不同路线的点概率不一定完全相同。

从表2 中可以看出观山湖区阳关大道在单位时间也即一个月中在不同天气下发生交通事故的不同次数的概率，但看不出明显趋势，因此对观山湖区阳关大道雨天单位时间内分别发生1次到100次事故的概率进行计算，并画出其概率密度图像。

表2 观山湖区阳关大道单位时间内发生事故次数概率表

如图3所示，观山湖区阳关大道单位时间也即一个月内发生交通事故次数的概率会随着次数的增加而增加，但达到一定次数后概率会随次数的增加而减少，而这个次数就是其分布的均值，而位于均值附近概率较大，符合泊松分布的特征。

图3 观山湖区阳关大道雨天发生交通事故概率密度图

3.2 整条道路发生交通事故的概率

求出每个事故点发生交通事故的概率后，需要利用点概率去寻求每条路线的线概率。考虑到每个点对一条路线发生交通事故的贡献值是不同的，其中一种较简单普遍的思想是，将每个交通事故点的发生事故概率值乘以对应的事故率做一个加权：

其中，i=1,2,3 表示3 条路线，j=1,2,…,k 表示每条路线上的事故发生点。利用此思想，可以得到3条路线在晴天、阴天、雨天3 种天气情况下发生交通事故的概率值。由于发生交通事故的概率越大，选择的驾驶路径越不安全，反之，不发生交通事故的概率越大，驾驶的安全程度也会越高。因此将不发生交通事故的概率作为选择路径的安全系数，这样可以更简洁直观，也就可以求出3条路线的安全系数值。

另一种思想就是利用上述的马尔可夫模型，将泊松分布中算出的事故点概率计算转移矩阵之后，也可得出3条路线在晴天、阴天、雨天3种天气情况下不发生交通事故的概率值，也即安全系数。

从表3的计算结果来看，当用加权方法求取安全系数时，在晴天时，第一、二、三条路线的安全系数分别是0.883 5、0.923 9、0.930 7，第三条路线安全系数最大，也即整条道路不发生交通事故的概率最大。因此晴天的时候应该选择安全系数大的第三条路线。同理阴天时选择第二条路线，雨天时选择第二条路线。

而当使用马尔可夫模型求取安全系数，在晴天时，第一、二、三条路线的安全系数分别是0.837 6、0.964 3、0.926 8，第二条路线安全系数最大，要选择第二条路线。同理阴天时选择第三条路线，雨天时选择第三条路线。

表3 推荐路径安全系数表

从上述两种方法均可以看出，不同天气下发生交通事故的概率有差距。

由于加权方法和马尔可夫模型方法所求得的各条路线的安全系数值有差异，故对于不同方法，决策者可以挑选其中概率最大状态作为考虑问题的出发点，选择对自己最有利的行动方案，即最大决策法[14-15]，取安全系数值最大的线路作为不同天气分类下的推荐安全路线。因此将表3 中不同天气下相同路线的最大安全系数提取之后得到表4。从表4中可以看出，不管是晴天、阴天和雨天，第二条路线的安全系数均大于第一条和第三条，分别为0.964 3、0.962 0、0.953 9，因此最终可以认为导航软件推荐的3条路径中，第二条路线是安全系数最高的，在出行过程中选择导航中的第二条路线最安全。

表4 推荐路径最大安全系数表

从导航软件推荐的路线来看，虽然导航软件推荐第一条路线，但第一条路线花费的行驶时间较长，距离相对于第二、三条路线也会更长。在现实生活中，车辆行驶的路线距离越长，经过的交通事故易发点会越多，使用的时间也越长，也会使得驾驶安全系数下降。而第二条路线的距离是最短的，驾驶时间也最短，其安全系数也最大。

4 总结

导航软件的路线基本基于路线距离最短、红绿灯最少、拥堵程度最小来推荐，往往忽略了道路上交通状态的变化情况，例如交通事故的发生。交通事故的发生不但会威胁生命财产安全，也会导致交通拥堵，使推荐的最优路线消耗更长的时间。

本文基于以月为单位的9个月数据进行研究，由假设检验得知单位时间内交通事故的发生数量服从泊松分布，因此建立泊松分布模型对道路上交通事故易发点发生交通事故的概率进行计算，并对不同点发生交通事故的贡献不同进行加权，求取整条道路发生交通事故的概率；而后发现事故点发生交通事故符合马尔可夫特性，故而建立马尔可夫模型计算整条道路不发生交通事故的概率，将两者的计算结果进行结合比较，在由最大决策法推荐的三条路线中，第二条路线安全系数最高，距离也较短，出行更应该选择第二条路线。

本文针对以人为本的安全路线选择规划推荐，充分考虑了所经道路中所有历史事故发生点以及不同类别天气对每条路线发生交通事故的贡献情况，计算出更为智慧安全的交通路线。如果可以提供更长且较细致的观测窗口内的数据，则可以提供更为精准的实时路线规划。如果可利用数据增大时，考虑将天气数据从日数据精细到时数据，利用每小时更新的当前天气情况，制定更为精准可靠的当前天气状况下的安全路线规划选择，模型预测的道路安全系数值将更为准确，更能有效降低交通事故发生率，减少交通拥挤所带来的资源消耗，满足人们的出行需求，实现“智慧交通”。

导航公司如果考虑将该模型算法加入导航推荐路线算法中，更能增加各导航软件的使用体验，可以提高最优路线的可靠度，为出行者提供更加科学、合理的优性决策，以此提升用户的信任度，增加用户量，提高自己的竞争力。