管道内检测器里程轮定位数据预处理算法设计
谢 雁,汪 伟,党 博,张 营,安 岑
(西安石油大学,西安 710065)
流体输送管道在工程领域应用广泛。为保证管道的正常运行,需要定期对在役管道进行损伤检测。管道内检测技术作为管道损伤检测的关键技术之一,为管道维护和管道完整性评价提供了重要参考[1-2]。在进行管道损伤检测作业时,需要对管道损伤位置进行实时定位,并且当内检测器在作业过程中遇到卡堵等故障时能够得到及时处理。解决上述问题的关键在于能够对工作中的内检测器进行有效地跟踪、定位。
国内外对管道内检测器的定位技术已经进行了大量的研究[3-8]。里程轮定位法是一种行之有效的定位方法,在管道内检测器定位方面得到广泛应用。在此基础上,融合多传感器定位技术,增加地面标记器,可以有效地提高管道内检测器跟踪定位的准确性。里程轮是安装在管道内检测器上用来记录里程的主要装置之一,其数据的准确性对管道内检测定位信息具有重要的影响[9-11]。
1 里程轮定位原理
管道内检测器利用管输介质驱动检测器在管道内运行,实时检测和记录管道的变形、腐蚀等损伤情况,并准确定位。里程轮装置安装在管道内检测器的尾部,当内检测器在管道中前进时,里程轮在弹簧预紧力的作用下紧贴管壁转动,将内检测器在管道中的轴向运动转换为里程轮的转动,使用传感器记录里程轮转动的圈数,将该圈数数据转换为内检测器在管道中的行进距离。里程轮定位原理如图1所示。
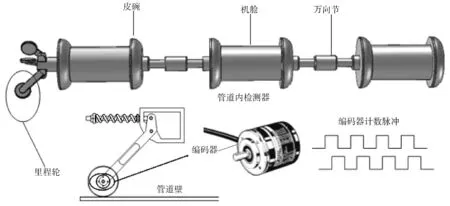
图1 管道内检测器结构及里程轮定位原理
在里程轮定位方法中,将里程轮和编码器同轴连接,里程轮每转动1圈,就会输出固定数量的脉冲。通过编码器记录脉冲数和里程轮的周长,可以得到内检测器在管道中的行进距离和速度等位置信息。为了提高里程轮定位的准确性和减小偶然性因素的影响,一般会在检测器上沿周向均匀安装多个里程轮来进行定位。理想情况下,里程轮的转动距离即为内检测器在管道中的行进距离。实际中,里程轮受管道内结蜡、油污、缺陷、焊缝等因素的影响,容易出现打滑等现象,导致里程轮数据存在测量误差,需要对其进行预处理。
2 里程轮定位数据预处理算法
管道内检测器在管道中工作时,里程轮数据会受到管道环境中随机因素的影响而存在随机误差。因此,可以从数学统计的角度出发对其数据进行处理,从而得到系统的最优估计。卡尔曼滤波算法提供了一种比较高效的、可用于计算的递归方法来实现对过程状态的估计,并且使得估计均方误差最小,可以有效地减小数据中随机误差的影响,适合里程轮定位数据的预处理。卡尔曼滤波是一种最优估计理论,其算法在时间域内,根据系统的观测数据,利用线性系统状态方程对系统状态进行最优估计。
卡尔曼滤波算法的思想是首先根据被测对象数学模型,以k-1时刻的最优估计X(k-1|k-1)为准,预测k时刻的状态变量X(k|k-1),同时又对该状态进行观测,得到k时刻的观测量Z(k),根据Z(k)对预测状态进行修正,得到k时刻的最优估算值X(k|k)。
基于卡尔曼滤波的管道内检测器里程轮定位数据预处理算法设计思想:通过一段时间间隔,计算这段时间间隔内的位移增量ΔS,将位移增量ΔS作为系统的测量值输入到卡尔曼滤波器,输出为系统状态的最优估计值。所以,可以将光电编码器检测位移过程描述为一个离散时间的随机过程,且测量过程中,过程噪声和测量噪声为互不相干的高斯白噪声,满足卡尔曼滤波的数学要求。卡尔曼滤波的基本思路如图2所示。

图2 卡尔曼滤波的基本思路
基于卡尔曼滤波的里程轮定位数据预处理算法数学建模过程如下。
状态方程:
X(k)=AX(k-1)+BU(k)+W(k)
(1)
X(k)=X(k-1)+W(k)
(2)
观测方程:
Z(k)=HX(k)+V(k)
(3)
Z(k)=X(k)+V(k)
(4)
式中:X(k)是k时刻的系统状态;U(k)是k时刻对系统的控制量,这里不考虑系统的控制作用,U(k)=0;A和B是系统参数矩阵,系统的状态不随时间变化,所以这里A=1;H是测量系统参数矩阵,包含噪声的观测量是状态变量的直接体现,所以这里H=1;Z(k)是时刻的观测值;W(k)和V(k)分别表示过程噪声和测量噪声,它们是高斯白噪声,协方差是Q和R。
根据第k-1时刻状态的最优结果X(k-1|k-1)预测第k时刻的状态X(k|k-1):
X(k|k-1)=AX(k-1|k-1)+BU(k)
(5)
X(k|k-1)=X(k-1|k-1)
(6)
根据第k-1时刻的误差协方差P(k-1|k-1)估计第k时刻的误差协方差P(k|k-1):
P(k|k-1)=AP(k-1|k-1)AT+Q
(7)
P(k|k-1)=P(k-1|k-1)+Q
(8)
式中:P(k|k-1)是X(k|k-1)对应的误差协方差;P(k-1|k-1)是X(k-1|k-1)对应的误差协方差。
计算卡尔曼增益Kg:
Kg=P(k|k-1)HT(HP(k|k-1)HT+R)-1
(9)
Kg=P(k|k-1)(P(k|k-1)+R)-1
(10)
计算系统k时刻的最优估计值X(k|k):
X(k|k)=X(k|k-1)+Kg(Z(k)-HX(k|k-1))
(11)
X(k|k)=X(k|k-1)+Kg(Z(k)-X(k|k-1))
(12)
计算系统k时刻的误差协方差P(k|k):
P(k|k)=(I-Kg·H)P(k|k-1)
(13)
P(k|k)=(I-Kg)P(k|k-1)
(14)
卡尔曼滤波算法作为一种最优化自回归数据处理算法,其算法可以分为2个部分:时间更新方程和测量更新方程。时间更新方程根据被测对象的数学模型,按照前一时刻最佳估计来预测当前时刻的状态估计;测量更新方程根据当前时刻观测结果,对预测状态进行修正,得到当前状态的最佳估计。
3 试验和结果分析
3.1 仿真分析
根据卡尔曼滤波算法流程编写程序进行试验。在试验过程中,选择100个测量值,验证算法的性能。卡尔曼滤波算法试验结果如图3所示。

图3 卡尔曼滤波算法试验结果
可以看到,相对于直接取用传感器的观测结果作为目标状态的值而言,通过卡尔曼滤波后获得的状态最优估计值要更加准确,状态波动小,较为稳定,更符合实际中管道内检测器的运行过程。
相对误差如图4所示。在本次试验中,直接观测结果与真实值之间的相对误差在8%以内,通过卡尔曼滤波算法确定的值与真实值之间的相对误差最大控制在2%以内,并且算法在迭代多次以后,算法趋于收敛,相对误差基本控制在1%以内,可见应用卡尔曼滤波算法处理过的里程轮数据其准确度更高。

图4 相对误差
3.2 误差分析
卡尔曼滤波算法在进行滤波时,也会产生误差,其误差主要包括:
1)模型误差。
在进行卡尔曼滤波时,由于对系统的特性了解不全面,使得所建立的数学模型不能充分地反映系统的动态特性,因此所建立的模型与实际不符,导致模型误差。
2)过程噪声协方差和测量噪声协方差取值造成的误差。
在进行卡尔曼滤波时,需要对过程噪声协方差和测量噪声协方差进行取值。从理论上来看,通过对整个系统过程的观测是可以得到准确的测量噪声协方差的值。由于没有办法直接对过程状态进行观测,所以无法得到准确的过程噪声协方差的值,有时只能通过选择给系统引入一定的不确定性,从而建立1个简单的过程模型而产生可以接受的结果。通过对以上2种情况的描述可以看出,在没有1个合理的标准来选择系数的情况下,可以通过调整滤波器的系数来调整系统的整个性能。
3)线性拟合误差。
在进行卡尔曼滤波时,需要所研究的对象是1个线性系统,但在实际中这样的系统往往难找。因此,一般都是通过对所研究系统进行线性拟合得到。由于线性拟合具有不确定性,会使卡尔曼滤波算法产生线性拟合误差。
4)其他误差。
在进行卡尔曼滤波时,计算机的舍入误差,离散化引入误差,如果有输入的话,输入的误差也会影响滤波的结果。
4 结语
本文研究的是基于卡尔曼滤波的里程轮定位数据预处理算法,根据里程轮定位数据误差,对里程轮运动状态进行建模,通过仿真试验,应用卡尔曼滤波算法进行里程轮数据预处理。仿真结果表明,该算法能较好地对里程轮数据进行预处理,抑制噪声干扰,提高里程轮数据的准确性,对管道内检测器准确定位具有重要作用。本次试验是仿真试验,测试数据不能完全代替实际数据。未来考虑更加符合实际管道环境,同时融合其它传感器信息,获得最佳估计算法。

