发明人专利文献耦合与发明人德温特分类号耦合比较研究——以非专利实施主体为例

宋艳辉，邱均平

（1.杭州电子科技大学管理学院，杭州310018；2.杭州电子科技大学中国科教评价研究院，杭州310018）

1 引言

文献计量学发展至今，许多文献计量学研究方法提出较早，并且经过了充分的研究与发展，已经相当成熟。然而，专利也是一种文献，将文献计量方法拓展到专利文献，探讨专利计量方法，是一件有意义的工作。发明人专利文献耦合源自文献计量学中作者文献耦合，作者文献耦合则是论文文献耦合基础上提出的。文献耦合，是指两篇论文引用了同一篇文献而形成了一种同引用关系，即耦合关系。文献耦合最早是由Kessler[1]于1963年提出来的。作者文献耦合将耦合的分析提升到作者层面，而不仅仅停留在论文层面，以论文的作者作为主要的对象[2]。拓展到作者层面后，文献耦合就变成了一种动态关系，随着论文的变化，作者文献耦合也在动态的变化，因此，作者文献耦合分析变得更加具有分析意义[3]。专利发明人如论文作者一样，具有强烈的标签意义。一般认为，论文作者的研究多为相对固定的，当然，一位作者可能拥有多个研究领域，研究领域也有可能发生迁移，但短时间就发生重大变化以及频频发生变化的可能性并不大。因此，论文作者成为了很多文献计量学者的重要分析与计量对象。

专利发明人之于专利，正如论文作者之于论文。专利发明人也往往具备相对固定的技术研究方向，因此，专利发明人是非常具有分析与计量价值的。除了专利文献容易发生耦合外，德温特分类号也是极易耦合的，在德温特数据库中，德温特分类号[4]是德温特调用大量的专业人士，将收入到德温特数据库中的专利信息进行深度加工，把来自不同国家不同语言的专利信息统一翻译成英语，尤其是对晦涩难懂的题名与摘要信息都以简明易懂的英语表达出来，并对专利的内容、新颖性和应用等方面进行提炼总结。其对每项专利都分配至少一个专利代码，有的专利涉及多个专利分类代码，人们可透过代码很容易辨析出专利所属的技术领域。因此，专利发明人、引文文献和德温特分类号构成了专利耦合的重要分析单元与关联关系，本文试从比较的角度，探究其之间的耦合关联关系。

2 国内外研究现状述评

国内外关于专利耦合的研究表现为三个方面的特征：①多为专利文献耦合。即以引文作为媒介建立耦合关系，借此测度技术相似性[5]、发掘技术机会[6]、识别新兴技术[7]，并对可能出现的技术突破进行预见[8]，或者侧重于企业的竞争情报分析[9]。②多为专利权人耦合研究。如温芳芳[10]曾经提出以专利权人类号耦合进行科学合作的探测，Huang等[11]较早使用专利耦合探讨高新技术，颜端武等[12]以专利耦合方法研究技术创新网络，Sternitzke等[13]将专利耦合与社会网络分析结合起来，进行过类似研究还有国内的陈云伟等[14]。③有对比研究，多为专利耦合与专利共被引的比较及融合。其中有代表性的是高楠等[15]建议融合专利共被引和耦合方法进行前沿识别，李睿等[16]从聚类的可操作性、稳定性、协同性等方面比较专利共被引与耦合方法。

从目前的研究可以看出，1994年Narin[17]最早提出专利计量的研究，之后Huang等[3]和孙涛涛等[9]进行了专利耦合的研究。关于专利耦合的研究远远没有成熟，还有很多值得研究的角度以及研究不足之处。例如，①大多数研究多侧重于方法的应用，对方法本身的探讨略显不足，也即是对基础理论研究不足。②多从专利权人角度进行耦合研究，实际上，专利发明人是专利的研发者，但并不一定就是实际拥有者，即并非专利权人，因此，对于具体研究专利的技术内容方面，或者其他的特定研究目的，专利发明人比专利权人将更有分析价值，能够得到更多的研究结论。③目前，有少数专利分类号耦合的探讨，如温芳芳[10]，但这些研究还是远远不够的，需要继续向前发展。因此，基于以上的研究不足，本文提出，从专利发明人的角度进行专利耦合的研究，从方法本身的探讨角度进行专利发明人文献耦合与专利发明人德温特分类号耦合的分析比较研究。德温特分类代码，是严格按照分类标准进行标注的，包含3个大类：工程、电子电气、化学，下分许多部，部下又分子类，共包含188个子类。德温特分类体系，由类→部类→子类构成一个完整的层级分类体系。如t01（digital computers）就是表示数字计算机技术领域，为子类层面的技术领域。本文的发明人德温特分类号耦合就是在子类层面的耦合。

3 数据来源与方法

德温特数据库（Derwent Innovations Index，DII）是本文重要的NPE专利数据来源。德温特数据库提供1963年以来至今的数千万条专利信息，而且是每周更新一次[18-19]。数据样本主要是NPE专利，NPE（non praticing enties）为非专利实施主体，其获取专利不以具体实施为目的，NPE将专利视为可以流转的商品，依靠专利交易活动赚取利润，其专利运营行为既可能是正当商业行为，也可能是滥用专利权的专利投机行为。选择非专利实施主体专利为例，主要是我们对其比较熟悉，以及其专利价值一般比较高，有利于我们对两种方法进行充分的讨论。我们的数据检索，采取高级检索途径，检索项为专利权人。以专利权人名称进行检索，可以避开非标准代码的非独一无二性，很多企业享有同样的非标准代码等问题。获取Eolas、Wi-Lan、Rambus、DataTreasury等NPE的 专 利 数 据[20]，共 获 得4624条专利数据，建立专利数据集，即样本数据。

与作者文献耦合分析相类似，发明人专利文献耦合表示，2位发明人在发明专利中因为引用了同一专利技术或者同一科学文献而形成了一种关系，我们称之为发明人专利文献耦合，需要指出的是，专利引文中既包含专利文献，也包含科学文献，发明人专利文献耦合也将科学文献计算在内。发明人类号耦合类似于作者学科耦合与作者关键词耦合，是指2个发明人使用了同一个分类号而建立的关系，这里的分类号为德温特分类号，一个德温特子类类似于科学文献中的一个学科或者一个主题词。在本文的研究中，我们对发明人专利文献耦合分析，命名为Inventor Bibliographic-Patent-Coupling Analysis，简称IBPCA；Bibliographic-Patent-Coupling意思是，耦合对象中既包含科学文献，又包含专利文献。发明人类号耦合分析，命名为Inventor Patent Classification-Coupling Analysis，简称IPCCA。

在耦合的计算方面，Zhao等[21]为每位作者分别建立数据集，数据集中包含作者的所有参考文献，两位作者数据集中相同的参考文献数量即二者之间的耦合频次。在IBPCA的计算中，发明人与作者是相对应的，论文中的参考文献与专利中的专利文献与科技文献是对应的：发明人—作者、论文参考文献—专利文献+科技文献。在IPCCA的计算中，每一个德温特分类号相当于一条专利引文，同样可以将分类号抽取出来建立数据集，跟专利引文数据集的建立过程与方法基本一致，其计算方法也是一样的。本文研究方法主要采用相关分析、因子分析、可视化分析方法。相关分析主要考察IBPCA、IPCCA的耦合总频次、平均耦合频次、最大耦合频次的相关性水平。因子分析主要是通过因子模型与残差分析考察IBPCA与IPCCA的拟合优度水平，通过因子载荷分析主要考察IBPCA与IPCCA在因子主题探测与发现上的异同。而可视化分析通过中心性测度发现因子主题的重要性以及相近与关联度，K核分析可以进一步探测核心主题。

4 实证分析

4.1 核心发明人析取

本文以普赖斯定律作为核心专利发明人的选定标准，统计NPE专利数据中的发明人，分两次统计：仅仅考虑第一专利发明人与考虑所有发明人。如果是仅仅考虑第一发明人，专利发明最多的是WARE,FA，拥有专利数量为144，则根据公式计算而得到m=8.99。如果考虑全部作者，专利发明最多的仍是WARE,FA，拥有专利数量为296，即nmax=296，根据公式计算而得到m=12.89。这2种方式，拥有的共同作者有68位，仅考虑第一发明人得到的74位核心专利发明人中，只有6位不在其中。虽然考虑了全部发明人之后，发明人数量多了很多，核心发明人也随着增多了起来，但是，通过第一专利发明人确定的核心专利发明人也同样是有效的。因此，我们进一步筛选出的这68位作者基本可称为NPE专利的杰出代表。此外，另一个相似之处是，这两种方式，确定的核心专利发明人所拥有的专利量，占所有专利总量的比例是相当的。仅考虑第一作者的占比为34.0568%，而考虑所有作者的占比为35.7052%。因此，专利发明人及其专利呈现一种良好的集中与离散分布。两种方式相互印证我们的结果是可信的。

4.2 耦合频次分析

分别计算每位发明人的耦合频次，如表1所示。平均耦合频次=耦合总频次/所有发明人-1，最大耦合频次为发明人在与除自身之外其他发明人建立的耦合频次中的最大值，自耦合采取自己最大耦合频次+1的方法，+1是为了增加自己与自己耦合的亲密性。表1显示，在IBPCA中，耦合频次最高的3位发明人是WARE,FA、HAMPEL,CE、ZERBE,JL，同时也是平均耦合频次最高的3位发明人；在IPCCA中，耦合频次最高的3位发明人为WARE,FA、BEST,SC、ZERBE,JL，同时也是平均耦合频次最高的3位发明人。我们发现，IBPCA中排名第1位与第3位的发明人同时也是IPCCA中的第1位与第3位。发明人较高的耦合频次，体现了发明人较高的研究活力，能够与其他发明人建立较多的耦合关系，因此，WARE,FA、HAMPEL,CE、ZERBE,JL、BEST,SC这些发明人是NPE专利技术中比较活跃的研究者。最大耦合频次又可称为最强耦合强度，表示了发明人与发明人之间的相似程度，只有2位发明人的研究极为相似才会反复地引用同一专利文献，或者反复地被归类于同一分类号。表1显示，IBPCA的最大耦合频次对为WARE,FA—BARTH,RM；IPCCA的最大耦合频次对为WARE,FA—PEREGO,RE。在最大耦合频次方面，WARE,FA依然表现出较高的研究活力，在IBPCA与IPCCA中，WARE,FA都是最强耦合强度对象，只是其发生对象有所不同。在IBPCA中，WARE,FA的最大耦合对象为BARTH,RM，与PEREGO,RE的耦合频次为575，排在了第3位，说明其与PEREGO,RE依然是非常相似的。在IPCCA中，WARE,FA的最大耦合对象为PEREGO,RE，与BARTH,RM的最大耦合频次为50，排在了第4位。因此可以认为，在IBPCA中的最大耦合频次对，在IPCCA中依然是较高的耦合频次对；而在IPCCA中最大耦合频次对在IBPCA也可以保持较高的耦合频次。通过以上分析，可以看到，IBPCA与IPCCA在耦合频次计算方面还是有一定的相似性，至少在高频次的发明人计算上呈现这种现象，那么从整体上分析是否仍然呈现出良好的相似性，即在较低频次的发明人耦合上也是否呈现这种态势，可以从下文的进一步分析中得到。

4.3 耦合相关分析

为进一步从整体上探析IBPCA与IPCCA的相关性水平，我们对68位发明人在IBPCA与IPCCA中的耦合频次以及耦合排名进行相关性分析，如表2所示。所有的相关性水平都是在0.01水平上的测度，Sig.值都远远小于0.01，即表示相关性是显著的。平均耦合频次是在耦合总频次的基础上计算而得到的，因此，耦合总频次与平均耦合频次的相关性是1，表示完全相关。其排名的相关性也是平均耦合频次排名跟最大耦合频次排名的相关系数也为0.817。这说明在IBPCA中，耦合总频次跟最大耦合频次之间是存在明显的相关性的，耦合总频次较高，最大耦合频次也容易较高。耦合总频次排名、平均耦合频次排名跟最大耦合频次排名的相关系数也都为0.927。这说明相关性是很高的，发明人在耦合中频次具有较高的排名，在最大耦合频次中也往往是拥有较高的排名。此外，发明人耦合频次排名的相关性要略高于频次值的相关性。在IPCCA中，发明人耦合频次排名的相关性跟频次值的相关性是相当的。在IPCCA中，耦合总频次与最大耦合频次的相关系数为0.751，耦合总频次排名与最大耦合频次排名的相关系数为0.749。这2个数值是极为接近的。在IPCCA中，发明人的耦合总频次比较高，最大耦合频次也是容易比较高的；发明人的耦合总频次排名较高，则发明人的最大耦合频次排名也容易较高。还可以发现，无论是IBPCA，还是IPCCA中，耦合频次（耦合总频次、平均耦合频次）与最大耦合频次都是存在较高的相关性的，耦合频次排名（耦合总频次、平均耦合频次）与最大耦合频次排名也都是存在较高的相关性的；但在IPCCA中，这种相关性水平要略低于IBPCA。换言之，发明人在IBPCA中，具有较高的耦合频次或者拥有较高的排名，则比IPCCA更容易获得较高的最大耦合频次及其排名。

表1 发明人耦合频次分布（前10位）

表2 耦合频次及排名相关性分析

加入专利量与专利量排名之后的相关性分析。可以看到，在IBPCA中，专利量与专利总频次、平均耦合频次的相关性要大于IPCCA。IBPCA的相关系数为0.779，而IPCCA的相关系数为0.570。而在专利量排名与耦合总频次排名、平均耦合频次排名的相关性相差不大，分别为0.479、0.579。这说明，在IBPCA中，专利量与耦合总频次、平均耦合频次的直接相关性更大一些，发明人拥有多的专利发明，其在耦合方面更易获得较高的耦合频次。而在排名方面，相比IPCCA，IBPCA则并不明显。在专利量及其排名与最大耦合频次及其排名的相关分析系数上（0.780、0.711，0.414、0.591）看，IPCCA则比IBPCA更具优势，也就是说，相对于专利文献耦合，在IPCCA中，拥有较多发明的发明人，更容易获得较高的最大耦合频次，在专利量排名较高，那么最大耦合频次的排名也往往具有较高的名次。

以上的相关分析并没有区分同一发明人在2种方法中的异同，实际上，分析同一发明人在不同方法中的表现，则更能体现着2种方法的异同点[5]。为进一步挖掘IBPCA与IPCCA的相似性，分析IBPCA与IPCCA的共有发明人，如表3所示。数据反映，显著水平是在0.01上的显著相关，Sig.远远小于0.01，表示相关性是存在的，IBPCA与IPCCA并非毫无关联。IBPCA与IPCCA的发明人耦合总频次相关系数是最高的，为0.618。IBPCA与IPCCA的发明人耦合总频次排名的相关系数为0.568。这表示，发明人在IBPCA与IPCCA中的耦合行为还是基本趋于一致的，发明人在IBPCA中的耦合总频次跟IPCCA中的耦合总频次在一定程度上是相关的，而发明人在专利文献耦合中的耦合频次排名与同一发明人在专利类号耦合中的频次排名也是保持了一定的相关性，也就是说变化并不大。

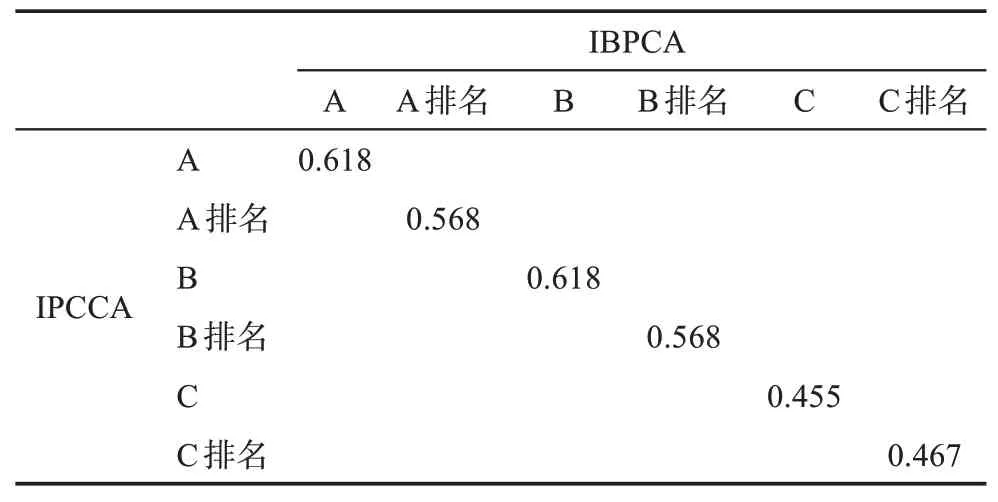
表3 IBPCA与IPCCA相关性对比分析

平均耦合频次是根据耦合总频次计算而得，因此，平均耦合频次与耦合总频次在IBPCA与IPCCA中的相关性分析结果保持一致。发明人在IBPCA与IPCCA中的最大耦合频次相关性分析结果分别为0.455；发明人在IBPCA与IPCCA中的最大耦合频次排名的相关性分析结果为0.467。这2个数值是极为接近的，而且相关系数并不高。这说明在最大耦合频次方面，IBPCA、IPCCA并不是一种强相关性关系。分析发现，有很多发明人在IBPCA有着良好的表现，而在IPCCA中表现并不佳，如SPINAR,B在IBPCA中的最大耦合频次排名为3，而在IPCCA中的却排在了63位，相差60位。这些发明人都会弱化发明人在IBPCA与IPCCA中最大耦合频次的相关性。当然，大多数发明人在IBPCA与IPCCA中的最大耦合频次及排名还是有着一定的相关性的。

4.4 IBPCA VS.IPCCA因子分析结果比较

分别构建68位发明人的IBPCA矩阵与IPCCA矩阵。对角线为发明人的自耦合[22]，对角线采取最大耦合频次加1的方式是较为合理的。分别对IBPCA矩阵与IPCCA矩阵进行相似性转换，消除数据在数量级与量纲上的差异。将相似矩阵导入SPSS进行因子分析，因子提取选用主成分分析。因子分析的旋转方法为直接Oblimin方法[23-25]。

4.4.1 模型拟合及残差分析

对IBPCA矩阵与IPCCA矩阵进行因子分析，碎石图如图1所示。从碎石图上看，IBPCA与IPCCA的模型拟合结果优度都比较理想。一条拟合优度理想的碎石图表现为，首先呈现陡峭地下降，并形成一个弧度，最后变成一条水平的直线。IPCCA的拟合结果要更优于IBPCA，因为IPCCA的曲线更为陡峭、急剧的下降，弧度的衔接更为平滑而直接，最后的直线也更水平。IPCCA碎石图也显示，曲线从第6个节点开始转为水平；IBPCA碎石图显示，从第10个节点之后在逐渐转平，但具体哪个节点并不能完全看出。IBPCA共提取了12个因子，共解释了90.138%的总方差；而IPCCA仅仅用5个因子，就解释了97.327%的总方差。相对于IBPCA，IPCCA可以用更少的因子，解释更多的总方差，方差的解释力度要更好。主成分分析模型提取的因子也一般是呈现由高到低的顺序排列，IBPCA提取的第一个因子也是最高的因子的特征值为23.672，占比34.811%的总方差，对应于图1a的第一个起点；IPCCA提取的第一个因子则为36.597，占比53.820%，并对应于图1b的首起点。IPCCA的第2个因子的特征值为20.695，占总方差的30.434%，即右图的第2个下降的节点，该节点距离第一个节点较近，高踞在上端，这2个节点就累积解释了总方差的84.254%。而IBPCA除第一个因子具有较高的解释力度外，其他11个因子的解释力度皆为一般水平。

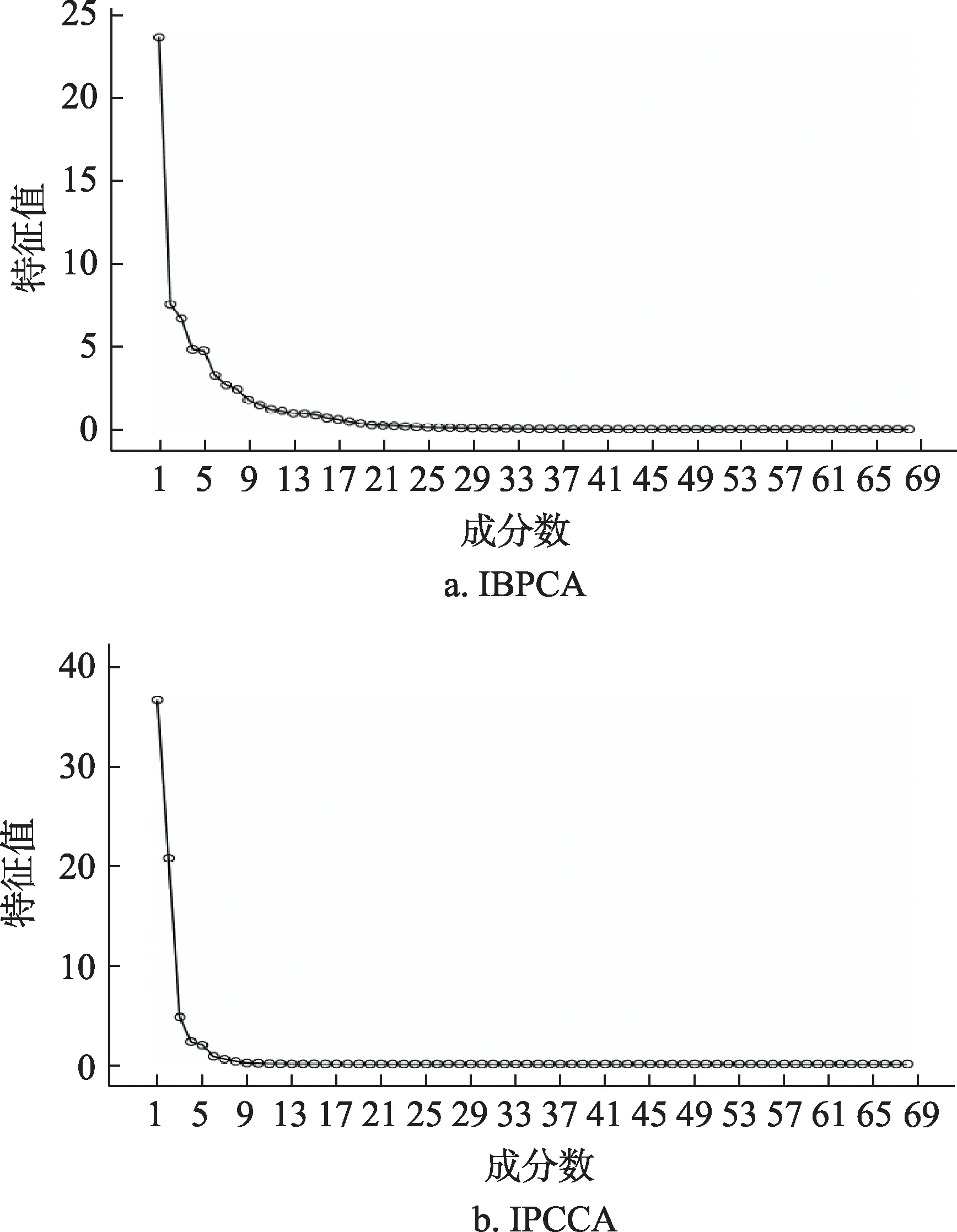
图1 因子拟合碎石图

本文从残差与公因子角度进一步分析比较IBPCA与IPCCA的拟合优度。IPCCA计算观察到的相关性和重新生成的相关性之间的参考，发现有20（0%）个绝对值大于0.05的非冗余残差；IBPCA计算观察到的相关性和重新生成的相关性之间的参考，发现有95（4%）个绝对值大于0.05的非冗余残差。因此，从残差上也显示IPCCA的结果要优于IBPCA。IPCCA通过因子分析提取的公因子也要比IBPCA理想。IPCCA的公因子变动范围为0.716～0.999，最高公因子为0.999，最低公因子为0.716；而IBPCA的公因子变动范围为0.482～0.992，最高公因子0.992也小于0.999，而最低公因子0.482也小于0.716。因此，从公因子变动范围、最高公因子、最低公因子上都显示IPCCA要优于IBPCA。

4.4.2 余弦相似度比较

余弦相似度（cosine similarity）是用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。重点考虑的是向量在方向上的差异而不是距离或者长度上的差异。如图2所示，对于向量d1、q、d2。如果d1、q、d2为二维空间的向量，那么d1与q、q与d2的余弦相似度为

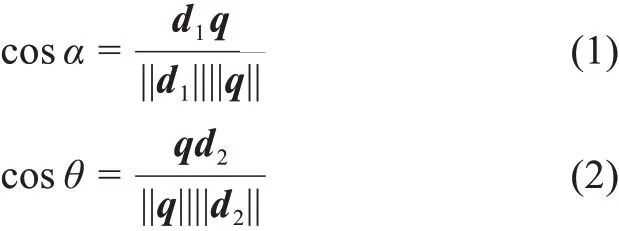
如果d1与q为坐标轴向量，轴坐标值分别为（m1,n1）、（m2,m2）那么d1与q的余弦相似度为

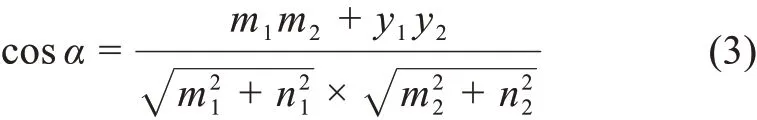
同理，可得到q与d2的余弦相似度。

如果d1=（X1,X2,…,Xn），q=（Y1,Y2,…,Yn），则

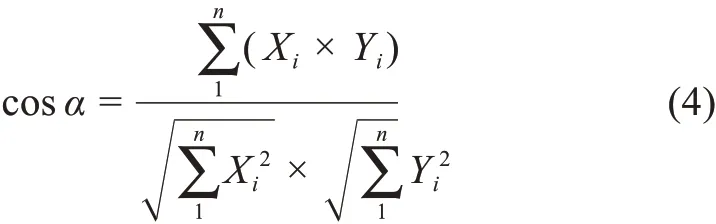
图2 余弦相似度图例

基于以上的理论，运行SPSS对IBPCA矩阵与IPCCA矩阵进行余弦相似度测度。结果显示，共有4624对数据，数据百分之百有效。这4624对数据是一一对应的关系，通过对4624对数据的计算与比对，结果表明IBPCA矩阵与IPCCA矩阵为相似矩阵，相似度为0.396。这是对原始数据矩阵的余弦相似度计算结果。我们认为，原始数据存在着较大的数据差异而会在一定程度上影响结果的表达，为消除数据在数量级与量纲上的差异，将相似性转化后的矩阵进行余弦相似度计算。计算结果果然要比原始矩阵的计算结果理想很多，相似性大大增强。因此可以说，通过对IBPCA与IPCCA矩阵余弦相似性的计算，基本可以断定IBPCA与IPCCA并不是毫无关系，是具有一定的相似性的。上文中，从耦合总频次、平均耦合频次、最大耦合频次等方面的相关性分析论证了IBPCA与IPCCA是相关的，可以说是从宏、中观层面的论证；而余弦相似度深入到每一个数据的比对与计算，可谓是从微观层面的论证IBPCA与IPCCA的相似程度。这都证明了IBPCA与IPCCA并非没有关系，而是具有一定关联的。

4.4.3 因子载荷分析

因子标签的确定，通过检查最高载荷发明人，考察最高载荷发明人与其他发明人（尤其是高载荷发明人）之间的高频次耦合对，分析这些发明人之间的共性，尤其是研究引发这些高载荷发明人发生耦合的专利文献内容，并咨询相关领域的专家学者，来确定因子的内容，IBPCA因子载荷分析如表4所示。

因子1：最大载荷发明人为CONNORS,DP，与WENTINK,M的耦合频次为76，与DALLY,WJ的耦合频次为46，与MAENG,J的耦合频次为40，与WARE,FA（载荷排名16）的耦合频次为最大耦合频次95。数字计算机与数据静态存储。因子2：最大载荷发明人为GARLEPP,BW，与ZERBE,J的耦合频次为276，与STOJANOVIC,VM的耦合频次为160，与STOCKHAM,MA耦合频次43，与WERNER,CW的耦合频次64。其中涉及最多的是信号生成与分布（TO1K）因子3：最大载荷发明人为SPINAR,B，与STANWOOD,KL的 耦 合 频 次 为1689，也是最大耦合频次为1689，与ONG,AE的耦合频次为181，与VOGELSANG,T的耦合频次为16。其中大量涉及的内容是数字信息传输（W01A），为通信领域。为避免混淆，区别于因子11（数据存储与传输，偏重计算机与半导体领域），定义该因子为通信数字信息传输。因子4、因子5不存在高载荷发明人，最大载荷发明人分别为LEE,W、BENYASSINE,A。因子6：最大载荷发明人为HYNECEK,J，主要检查HYNECEK,J与COK,RS、HOSSAIN,M的共同技术研究来确定因子为半导体与集成电路。因子7，也不存在高载荷发明人，重点研究SU,H、GAO,Y共同的专利发明。因子8、因子9、因子10、因子12因子载荷普遍体低于0.4，并不存在高载荷发明人。因子11，最高载荷发明人为WEBSTER,MA，涉及最多的是数据存储与内存、互连、数据传输（T01H）、数据静态存储（U14A），可以看到，虽然二者属于不同的大类，但内容还是有很多交叉的，因子内容可以归纳提炼为“数据存储与传输”。因子4、因子5、因子7、因子8、因子9、因子10、因子12。本文集中统一标注因子内容，因为研究发现这7个因子都是源自SHLOMOT,E、GAO,Y、SU,H、THYSSEN,J、BENYASSINE,A这5位发明人，这些因子是相对独立的，且因子载荷分布比较均匀。因子标签的确定我们首先主要考虑最高载荷发明人与耦合频次最高的发明人之间的共性研究，当因子之间发生冲突时，如因子10与因子12的最高载荷发明人，以及最高耦合对可能同为SHLOMOT,E、GAO,Y，我们再考虑第2或者第3载荷发明人的研究。如此下来，确定因子标签为，因子4为“计算机语音处理”，因子5为“一般语音处理”，因子7的载荷作者过少并且载荷值过低难以确定研究内容，以“未查明”来表示，因子8为“便携式手机”，因子9为“噪音处理”，因子10为“编码与信息论”，因子12为“数据转换与传送”。

表4 IBPCA因子载荷分析

IPCCA因子载荷分析如表5所示。因子1：LAU,BC是最大载荷发明人，最大耦合频次为22，LAU,BC与KIZER,JM耦合频次为19，与STARK,DC的耦合频次为21，与KIM,J的耦合频次为16，与BEST,SC的耦合频次为22。因子2：GAO,Y是最大载荷发明人，最大耦合频次为51，与CONNORS,DP的耦合频次为27，与MONRO,DM的耦合频次为51，与SHLOMOT,E的耦合频次为30。因子3：分析高耦合发明人共同的技术研究，尤其是BELL,M与ARMSTRONG,BA研究发现，耦合最多的是数据存储与内存、互连、数据传输（T01H）、数据静态存储（U14A），因子内容可以归纳提炼为“数据存储与传输”，既涉及数字计算机领域，又涉及半导体与电子电路，是二者的交叉领域。因子4：只有2位发明人，分别是STOCKHAM,MA、HIDER,RC。STOCKHAM,MA是最大载荷发明人，而最大耦合频次对象也恰好是HIDER,RC，频次值为4。分析STOCKHAM,MA与HIDER,RC交合的研究，多为B大类的环系化合物研究。因子5：耦合较多的技术领域为：液晶显示器（U14-K01）、光学（X26）。因子内容可以为“LCD光学研究”。

4.4.4 可视化分析

运用NERDRAW对因子矩阵进行可视化展示。因子用圆形节点表示，发明人用方形节点表示。圆形节点与方形节点之间的连线，表示该发明人在该因子上具有载荷，且载荷值要大于0.2才会出现。连线的粗细代表因子载荷值的大小。因子用统一的颜色表示。方形节点的颜色代表不同的点中心性，红色表示点中心性为1，军绿色节点表示点中心性为2，粉色节点表示点中心性为3，黄色节点中心性为4，深蓝色节点的点中心性为5，荧光色节点的点中心性为6。节点的大小代表中间中心性。

在IBPCA可视化图谱（如图3所示）中，通过中间中心性分析之后，可以发现3个比较重要的因子：数字计算机、通信数字信息传输、数据存储与传输。通过后文的K核分析，也会发现这3个因子是最为重要的。这3个因子相互作用，交织在一起。联系通信数字信息传输、数据存储与传输的发明人是VTANWOOD,KL，ARYANFAR,F。联系数字计算机、数据存储与传输的发明人比较多。联系数字计算机、通信数字信息传输的发明人是WENTINK,M。数字计算机与“半导体与集成电路”也是比较密切的，有很多联系发明人。

表5 IPCCA因子载荷分析

图3 IBPCA可视化图谱(彩图请见http://qbxb.istic.ac.cn/)

在IPCCA可视化图谱（如图4所示）中，最为重要的因子为：数字计算机、通信数字信息传输。这也是相互作用最强的2个因子。中间有众多的发明人相互联系，这跟IBPCA是不一样的。IBPCA仅有一位发明人联系，2个因子之间的相互作用明显比较弱。“数据存储与传输”与数字计算机的作用比较强，中间联系的发明人有W00,SC、TSERN,EK、SHAEFFER,I、OH,KS、PEREGO,RE、BARTH,RM。“数据存储与传输”与通信数字信息传输的相互作用也比较强，中间联系的发明人有MONRO,DM、SHUSTER,GS、MAENG,J、COK,RS。这几位发明人同时也是联系数字计算机与通信数字信息传输的重要发明人。

可以看出，IPCCA探测到的最为重要的因子为：数字计算机、通信数字信息传输，在IBPCA中都有探测到。IPCCA探测到的数据存储与传输，在IBPCA也有探测到，该因子在IBPCA是中重要因子。IPCCA探测到的LED光学研究，在IBPCA中并未探测到。IBPCA探测到很多小的因子，如便携式手机、一般语音处理、计算机语音处理、编码与信息论、数据转换与传送、噪音处理等，在IPCCA中也查询不到。因此，可以说，IBPCA能比IPCCA探测到更多因子，尤其是小的因子。因子之间的相互作用也是不一样的，在IPCCA相互作用强，未必会在IBPCA中表现出强作用力；在IBPCA中作用力强，也未必会在IPCCA表现出强作用力。

本文进一步进行K核分析，可以得到更为核心的研究领域及发明人。分别进行K=1与K=2,5的计算就可以看到IBPCA的核心研究领域（因子）有4个分别是：数字计算机、通信数字信息传输、数据存储与传输、半导体与集成电路。而进行K=3与K=1,2的计算，IPCCAK也发现了3个核心研究领域：数字计算机、通信数字信息传输、数据存储与传输。因此，可以看出IBPCA与IPCCA发掘的核心领域大体是相当的。

5 结论

本文以NPE专利为例，探析发明人专利文献耦合与德温特分类号耦合，主要的研究结论如下：

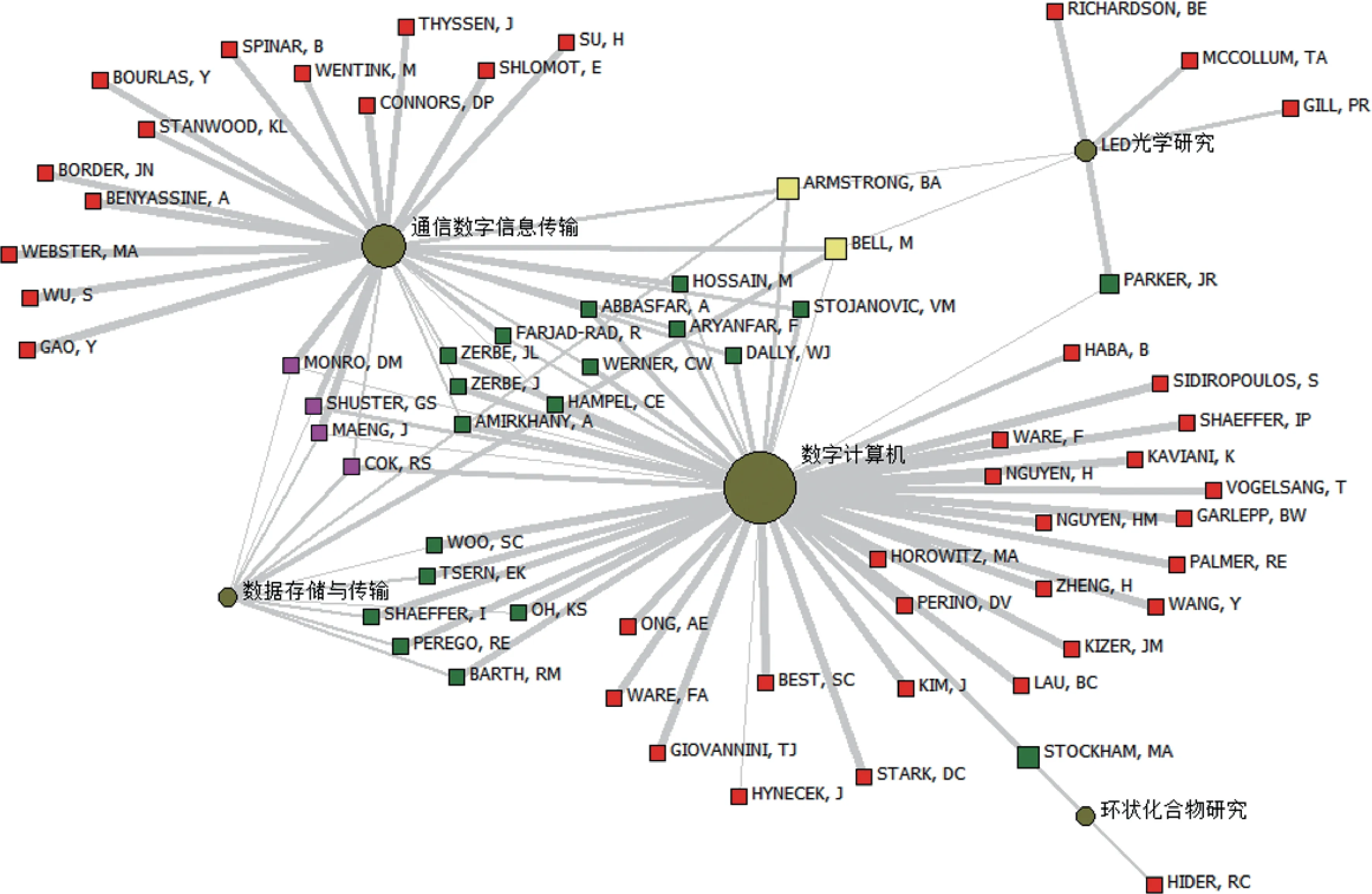
图4 IPCCA可视化图谱(彩图请见http://qbxb.istic.ac.cn/)

（1）从专利量及其排名、耦合总频次及其排名、平均耦合频次及其排名、最大耦合频次及其排名的相关分析结果显示，IBPCA与IPCCA是具有相关性，相关水平会略有不同。例如，耦合频次与最大耦合频次都是存在较高的相关性的，耦合频次排名与最大耦合频次排名也都是存在较高的相关性的，而最大耦合频次在二者之中却呈现弱相关，平均耦合频次与耦合总频次趋于一致。

（2）IBPCA与IPCCA的模型拟合结果优度均比较理想。IPCCA的拟合结果更优于IBPCA。IPCCA可以用更少的因子，解释更多的总方差，方差的解释力度要更好。公因子变动范围、公因子大小等也显示IPCCA要优于IBPCA。余弦相似度从微观层面揭示了IBPCA与IPCCA的相似程度。

（3）IBPCA能比IPCCA探测到更多主题，在规模较小的主题上发现更具优势，规模小的主题往往体现了前沿领域。IBPCA与IPCCA中主题的相互作用会有差异，强弱难辨，即在IPCCA相互作用强，未必会在IBPCA中表现出强作用力；在IBPCA中作用力强，也未必会在IPCCA表现出强作用力，需要进一步的实证研究。

（4）IBPCA与IPCCA发掘的NPE核心领域大体是相当的。IBPCA的核心研究领域有4个分别是：数字计算机、通信数字信息传输、数据存储与传输、半导体与集成电路；而IPCCA也发现了3个核心研究领域：数字计算机、通信数字信息传输、数据存储与传输。这些主题基本代表了NPE研究的核心所在。

本文是文献计量学方法向专利文献领域拓展的有益尝试，并希望专利耦合最终能像文献耦合那样成为成熟的方法得以广泛应用。本文提出的发明人专利文献耦合与发明人德温特分类号耦合在未来能够在专利文献结构探测方面发挥重要作用，而且这两种方法各有特点，也各有优势，如果能结合起来使用将会取得比较好的研究结论。同时，本文也存在一定缺点和不足：一是仅仅选择了德温特数据库进行实证研究；二是人名虽然根据机构进行过清洗，但难免会有错误与遗漏。这些不足之处有待在未来工作中做进一步完善。