基于DBSCAN与HL相结合的晶圆成品率预测研究
姚晓童,李 林
(上海理工大学 管理学院,上海 200093)
成品率是半导体制造过程中一项重要的工艺性能指标,精准预测晶圆成品率对于改进生产工艺、减少晶圆制造损失具有重要意义。
目前成品率建模大多基于影响成品率的关键参数,如缺陷数量、大小、电性参数等。文献[1]考虑缺陷概率密度分布建立了经典的泊松成品率预测模型,由于模型结构简单,应用最为广泛,但预测准确度较低。文献[2]考虑缺陷分布存在过度分散性,对文献[1]进行了改进,建立了广义泊松分布模型预测晶圆成品率,提高了成品率的预测精度。文献[3]基于缺陷类型、大小、位置等基本信息建立因果统计模型,进行成品率的预测,并提出了成品率优化策略,但由于缺陷数据量庞大,模型求解困难。文献[4 -5]考虑晶圆电性测试的关键参数,以最小化测试参数和预测误差为目标,选取显著特征向量,进而预测晶圆成品率,但电气参数数据对象多,对象间关联性强,导致模型预测准确度较低。文献[6]基于成品率历史数据提出一种混合聚合–熵–共识的模糊协同智能算法,首先得到成品率预测区间,然后用反向传播网络去模糊化得到成品率的预测值,具有较好的预测精度。影响晶圆成品率因素众多,数据量大且关系复杂,但缺陷数据仍然是成品率建模最具影响力的因素[7]。
为提高预测精度以及确定晶圆缺陷来源,部分学者考虑晶圆缺陷的聚集性建立成品率预测模型。文献[8]考虑晶圆缺陷的邻近效应,利用缺陷模式建立成品率模型,具有较高的预测精度。文献[9 -10]通过分析晶圆图,识别缺陷模式,帮助管理者确定减少缺陷任务的优先级以提高晶圆成品率。以上研究表明,考虑晶圆缺陷聚集特性,不仅可以快速查找缺陷来源,且模型预测精度高。但以上成品率模型均是在晶圆水平进行建模,仅考虑晶圆缺陷的一种模式。晶圆生产过程复杂,一片晶圆通常会存在多种缺陷模式,在晶圆水平进行建模在一定程度上降低了模型的预测准确度,难以获得全面的缺陷损失来源。实际生产过程中,缺陷数据存在嵌套结构[11],即同组晶片缺陷模式具有相似性,现有文献大多都没有考虑缺陷数据嵌套结构特性。
本文考虑缺陷聚集性和数据的嵌套结构,首先用基于噪声的密度聚类(density-based spatial clustering of applications with noise,DBSCAN)算法识别缺陷模式,将缺陷计量数据按缺陷模式在晶片水平汇总,基于缺陷模式和缺陷数量建立多水平逻辑回归(Hierarchical Logit,HL)晶片失效概率模型,研究引起晶片失效的主要缺陷模式、关键工序,进而完成成品率的预测。
1 问题描述
在半导体行业中,计算机辅助制造会产生海量数据集,通常每个数据集不能直接用来预测成品率,需要对不同数据集进行有效整合,如何获得可行数据是成品率建模复杂的原因之一。本文所用数据集为产线缺陷监控系统数据和电气参数测量数据。缺陷监控系统有两种:一种是以缺陷为单位的缺陷记录数据库,该系统主要记录了缺陷的大小、缺陷的类型以及缺陷的位置等基本信息;另一种为缺陷分析工程师使用光学显微镜扫描晶圆得到晶圆图(wafermap),分析晶圆图可以识别不同的缺陷模式,例如线性缺陷、团状缺陷等,帮助工程师定位缺陷来源。电气参数测量数据指在晶圆加工完成后,对晶圆上每个晶片进行针测,以检查晶片的性能,根据针测结果将晶片划分为不同的bin值。考虑晶圆缺陷聚集特性,本文用DBSCAN算法对晶圆缺陷进行聚类获取晶片缺陷模式;将在线缺陷检测系统中的缺陷在晶片水平进行汇总,即获得每个晶片缺陷数量;根据晶圆针测数据集获取每个晶片bin值,最后将晶片缺陷模式、晶片缺陷数量以及晶片bin值3个数据集进行整合,得到适用于成品率建模的数据集。
基于缺陷计量数据成品率建模通常会假设缺陷数据是独立的,但在晶圆实际生产过程中,缺陷数据是呈嵌套结构存在的,例如晶片嵌套在晶圆上,晶圆组合在批次中。因此,不同批次或者不同晶圆上的晶片并不是相互独立的,晶圆嵌套结构数据如图1所示。图中:ynijkt表示第t个产品、第k个批次、第j个晶圆、第i个组别的失效晶片;nj表示第j个晶圆失效晶片的数量;N表示失效晶片总数。在该结构中,不同组的缺陷数据呈差异性,同组缺陷数据呈聚集性,HL模型可以解决嵌套结构数据组间非独立性与组内聚集性[12]。为此,本文建立了HL成品率预测模型,该模型还可帮助企业识别显著性批次、组别,以快速定位关键工序。

图1 多层次晶圆结构Fig.1 Multi-level wafer structure
2 晶圆缺陷模式识别
2.1 晶圆缺陷聚集特点及划分依据
晶圆缺陷聚集性表现为具有明显的簇、缺陷点集中和簇中点密度大。晶圆缺陷模式主要分为随机缺陷、局部团状缺陷、线性缺陷、边缘环状缺陷以及粒子缺陷。5种缺陷模式划分[13]的主要依据如表1所示。

表1 5种缺陷模式主要特点及划分依据Tab.1 Main characteristics and classification basis of 5 defect modes
基于噪声的密度聚类算法可由密度可达关系找出最大密度相连的集合,不需要指定聚类个数,在有噪声的情况下可识别出任意形状的簇。
2.2 DBSCAN聚类算法
假设邻域为ε,聚类密度阈值为 minPts,缺陷点集为T={oi},i=1,2,···,6,对缺陷点进行相关定义。
a.邻域:缺陷点o1,o2∈T,如果点o2与o1的距离不大于ε,则o1的 领域可表示为Nε(o1)={o2∈T|d(o1,o2)≤ε},d为缺陷点之间的距离。
b.核心对象:如果缺陷点o1的邻域内至少存在minPts个缺陷点,则o1是一个核心对象。
c.密度直达:如果缺陷点o2在 缺陷点o1的邻域内,且o1点 为核心对象,则称o2由o1的密度直达。
d.密度可达:存在缺陷点序列o1,o2,o3,o4,o5,o6。在这个序列中,每一个缺陷点都与它前一个缺陷点密度直达,则称o1与o6密度可达。
e.密度相连:如果缺陷点o1与缺陷点o6密度可达,缺陷点o2与缺陷点o6密度可达,则o1与o2密度相连。
f.簇:由所有密度可达的缺陷点导出的最大密度相连的点集合为一个簇。对于不属于任何一个核心对象邻域的缺陷点标示为噪音点。
通过实验法调整邻域 ε与密度阈值 minPts完成晶圆图所有缺陷点聚类,形成分类簇。将分类簇根据表1划分缺陷模式(将小于密度阈值的缺陷点划分为粒子缺陷),获得各个缺陷点分类。
3 Hierarchical Logit模型
逻辑回归模型常用于晶圆成品率建模,但它的基本假设为数据是相互独立的。考虑晶圆缺陷数据嵌套结构和聚集性,本文使用多水平逻辑回归构建晶圆成品率模型。多水平逻辑回归是广义混合线性模型的一种。
广义混合线性模型主要由抽样模型、结构模型和连接函数3部分组成。抽样模型是指反应变量服从某一指数族分布,本文晶圆成品率为二分类问题(晶片pass/fail),定义 φnijkt为第t个产品、第k个批次、第j个晶圆、第i个组别、第n个晶片的失效概率,yj代 表第j个晶圆上有mj个缺陷晶片的失效晶片数量,则yj服 从有mj次实验、每次实验成功概率为 φn的二项分布

采用Logit连接函数,即

式中,ηnijkt为晶片失效概率的对数发生比,ηnijkt=。 φnijkt取值范围为(0,1),当φnijkt>0.5时,晶片失效。
结构模型是解释变量与自然参数的线性表达式,与广义线性模型不同的是,广义混合线性模型的结构模型包括随机效应与固定效应两部分。当不定义随机效应时,广义混合线性模型变为广义线性模型。通过晶片组合在晶圆上,晶圆嵌套在批次上,批次嵌套在产品层建立嵌套变量,假设不同层次不同组别的晶片是相互独立的,同组内晶片具有相似性。在批次层、晶圆层和组别层建立嵌套变量的随机截距模型,在产品层引入晶片大小变量,构建非随机变化斜率与截距模型。
多层次晶圆晶片失效概率的对数发生比综合线性模型为[12]

式中:wt表示晶圆特征尺寸;xnijkt表示晶片缺陷数 量;π00000为 截 距 项,πl0000(l=1,2,3,4,5)表 示 第l个缺陷模式的自然参数;π00001表示产品大小的自然参数; πl0001(l=1,2,3,4,5)表示产品层与个体层交互效应的自然参数;r0ijkt,e00jkt,u000kt分别表示失效概率对数发生比在批次层、晶圆层、组别层的随机效应参数。
第j个晶圆成品率Yj可表示为

式中, E(φj)表示在第j个晶圆上晶片失效概率的期望值。
使用SAS 9.1软件NLMIXED过程构建模型。选用极大似然估计算法与对偶拟牛顿优化算法进行模型求解,使用比值比(odds ratio)解释特征向量对晶片失效概率的影响,如式(5)所示。比值比代表当晶片为第l个缺陷模式时,缺陷数量增加一个单位会影响晶片失效概率的增加值。选用Pearson卡方统计量与AIC信息准则指标评价模型拟合优度[13]。

式中:QOR表示被检验的解释变量的比值比;odds表示晶片失效发生概率与不失效概率之比。
4 仿真实验及结果分析
本文缺陷数据样本选自某晶圆厂实际生产线监测系统,包含 3种不同工艺尺寸产品,15个批次,30个晶圆。3种不同工艺尺寸产品分别可划分出2480,848,533个晶片。首先对30个晶圆图进行密度聚类,共识别出4578个缺陷晶片。将产品1与产品2作为训练集,产品3作为测试集。训练集数据共包括3599个缺陷晶片,测试集数据共包含979个缺陷晶片。
4.1 晶圆缺陷模式识别
基于DBSCAN对每个晶圆图进行聚类,根据实验法确定邻域ε,聚类密度阈值 minPts,部分晶圆缺陷晶片聚类结果如坐标图图2所示。

图2 晶圆聚类结果Fig.2 Wafer clustering results
每张晶圆图具有多种缺陷模式,结合表1可知:图2(a)属于环状缺陷与随机缺陷;图2(b)属于线性缺陷;图2(c)属于随机缺陷和局部团状缺陷。根据晶圆图获取每个缺陷晶片的坐标、缺陷模式、到中心的径向距离,并根据径向距离对晶片分组,分组界限为半径的一半。
4.2 数据聚合及异常值检测
本文将在线缺陷测量数据与晶片针测数据基于晶片缺陷模式进行整合,以获取适用于缺陷建模的数据。部分缺陷原始数据如表2所示,加粗部分为位于同一晶片上的不同缺陷的数据。利用Excel数据透视表功能对其进行聚合,缺陷测试数据与晶片针测数据整合后的数据如表3所示。根据晶片聚类结果,对表3数据进行整合,整合后的数据为HL模型的输入数据,如表4所示。
为了提高预测精度,对数据进行分析与预处理,将异常值在数据中剔除。对训练数据集进行统计分析,每个晶片中存在缺陷均值为2.8,中位数为1,分位数为1,分位数为2,最小值为1,最大值为144。可见,在训练数据集中存在大量异常值。为消除异常值对模型的影响,采用one-side trimmed均值异常值检测方法剔除异常值。该方法统一了数据集中的均值与中值,其效率优于中值法异常值检测[14]。本文设置p值为5%,根据统计分析结果,95%的晶片缺陷数在5以内,所以将晶片缺陷数大于5的晶片样本在训练集中删除。为验证模型方法的有效性对测试集数据不作处理。

表2 缺陷原始数据Tab.2 Defect raw data
4.3 回归结果分析
4.3.1 Logit回归

表3 聚合后数据Tab.3 Aggregated data
为了探讨该数据集是否需要使用多水平Logit回归,首先对训练集数据作一般Logit回归分析。模型输入参数为产品编号、批次编号、晶圆编号、组别、晶圆特征尺寸以及缺陷模式,其中晶圆特征尺寸为标准化后的数值。实验结果表明,模型拟合优度检验Pearson卡方p值为0.009,但预测准确率达90.83%,表明模型没有充分利用样本数据,模型拟合优度表现不优,AIC指标值为2423.61。Logit模型显示晶圆1、晶圆2、组别3、组别7、组别9、组别15、组别19、组别23、随机缺陷模式、团状缺陷模式、线性缺陷模式、环状缺陷模式以及粒子缺陷模式因子具有显著性(p<0.1)。

表4 模型分析数据Tab.4 Model analysis data
4.3.2 Nested Logit回归
考虑缺陷数据嵌套结构,在Logit回归模型中加入嵌套变量,Nested Logit模型输入参数为产品编号(批次编号)、批次编号(晶圆编号)、晶圆编号(组别)、晶圆特征尺寸以及缺陷模式,输入数据集为剔除异常值后的训练集。与Logit模型相比,Nested Logit模型给出了更加精确的信息,不仅识别出重要的批次、晶圆信息,同时给出产品1的批次1与其他批次有显著差异,批次1中的晶圆1、晶圆2有显著差异。对于同一片晶圆,不同组别晶片失效概率差异较大,这些信息可以帮助企业工程师找出潜在的质量偏差,进而在制造过程中进行故障排除。在显著性水平 α=0.1下,Nested Logit回归模型识别出产品1(批次1)、批次1(晶圆1)、批次1(晶圆2)、晶圆1(组别2)、随机缺陷、团状缺陷、线性缺陷、环状缺陷以及粒子缺陷解释变量具有显著性。Nested Logit回归模型的Pearson卡方p值为0.128,表明Nested Logit 模型对数据拟合较优,AIC指标值为1902.191。该模型AIC指标值小于Logit 回归模型的AIC指标值,p值更加显著,表明Nested Logit回归模型优于一般Logit回归模型。
根据Nested Logit回归模型显著性因子构建晶片失效概率模型,由于产品编号、批次编号、晶圆编号、组别等变量对于每个数据样本都是不同的,因此利用随机缺陷、团状缺陷、线性缺陷、环状缺陷以及粒子缺陷因子构造晶片失效概率模型为

式中,ηn=−4.4321+1.4199xn+1.4203xn+1.377xn+1.1566xn+0.8149xn。
4.3.3 Hierarchical Logit回归
Nested Logit回归模型的基本假设为同组内的晶片是相互独立的,但在晶圆生产过程中所产生的系统缺陷通常是集群存在的,且Nested Logit回归模型没有考虑产品层与个体层的交互效应,在实现多产品的混合预测方面有待进一步考察。
本文所构建的HL回归模型的固定效应参数包括晶圆特征尺寸、缺陷模式、晶圆特征尺寸与缺陷模式交互变量,随机截距模型参数为产品编号(批次编号)、批次编号(晶圆编号)、晶圆编号(组别)。结果显示:随机效应参数中晶圆编号(组别)和产品编号(批次编号)具有显著性,协方差估计分别为(0.2584,0.1053),表明缺陷模式斜率受产品层和组别层(晶片失效概率组均数)影响较大;但批次编号(晶圆编号)不具有显著性,表明在批次层和晶圆层晶片失效概率组间差异不大。在显著性水平 α=0.1下,HL模型识别出产品1(批次1)、晶圆1(组别2)、晶圆2(组别2)、随机缺陷、团状缺陷、线性缺陷、环状缺陷以及粒子缺陷、晶圆特征尺寸、晶圆特征尺寸以及随机缺陷、晶圆特征尺寸以及团状缺陷、晶圆特征尺寸以及线性缺陷、晶圆特征尺寸以及环状缺陷解释变量具有显著性(p<0.1)。 Pearson卡方p值为0.79,模型的拟合优度提高,在显著性0.05下,该模型基于缺陷数据拟合晶片失效概率是合适的。AIC指标值为1692.5,小于Logit 回归模型AIC指标值与Nested Logit回归模型AIC指标值,因此,HL回归模型拟合更优。
在显著性水平 α =0.1下,使用固定效应参数因子构建晶片失效概率,模型为
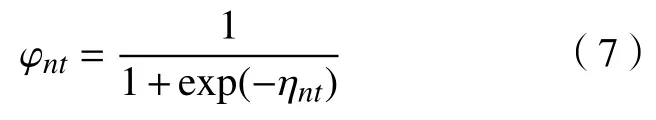
式中,ηnt=−4.4155+0.553wt+1.5424xn−0.2498wt·xn+1.3376xn−0.2159wtxn+1.3267xn−0.2433wtxn+1.138xn−0.1694wtxn+0.6889xn。
4.4 成品率预测及分析
根据模型(6)与模型(7)预测测试集晶片失效概率,通过式(4)计算每个晶圆成品率。HL回归模型、Nested Logit回归模型与Seed’s模型对测试集中每一个晶圆的缺陷晶片pass数预测值,如图3所示。图4展示了HL回归模型、Nested Logit回归模型与传统成品率预测模型Seed’s模型[1]对测试集中每个晶圆成品率的预测情况。
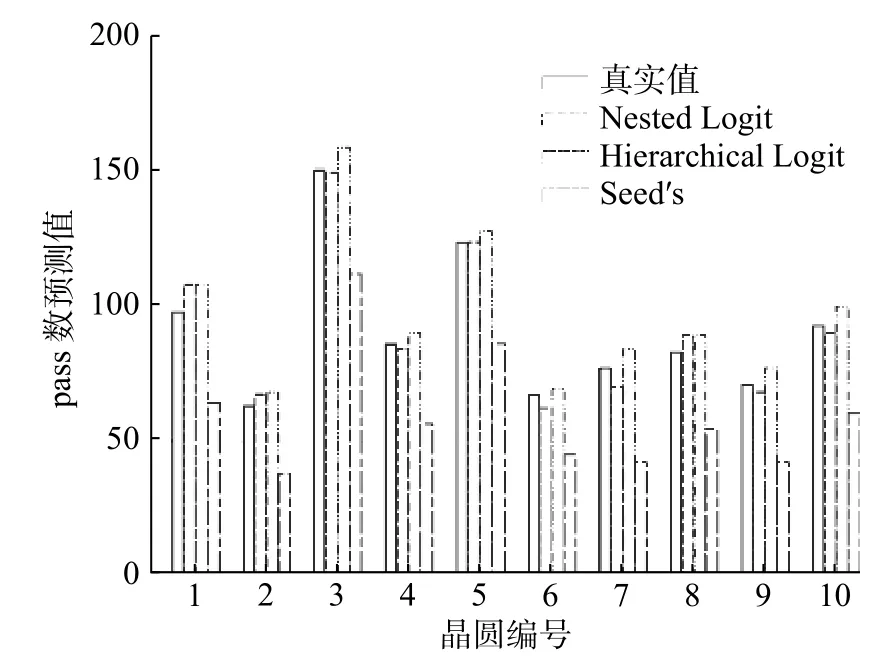
图3 晶圆预测通过数Fig.3 Number of wafers predicted to pass
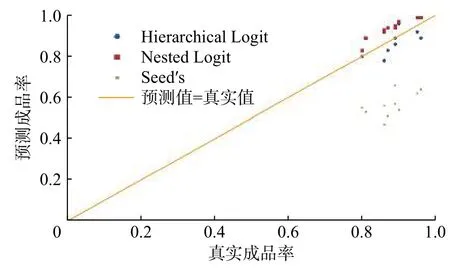
图4 测试集晶圆成品率预测值Fig. 4 Predicted yield of the test set
由图3和图4可以看出Seed’s模型成品率预测值低于成品率实际值,而低估成品率会增加厂商缺陷分析成本。Nested Logit回归模型的成品率预测值比真实值高,预测偏差比Seed’s模型低,预测准确率较高。因此,考虑晶圆生产过程的嵌
套结构可以提高成品率预测精度,同时可辅助工程师决策,但未考虑产品层与个体层的交互效应和缺陷数据的组内聚集性,可适用于单一产品的预测。本文提出的HL模型成品率预测值与实际值最为接近,预测偏差远小于Seed’s模型,比Nested Logit回归模型预测更加精确,可适用于不同产品成品率预测,具有更高的预测能力与可行性。
根据HL模型实验结果得出,缺陷分析工程师应重点关注产品1的批次1。分析产品1批次1,晶圆缺陷模式多为团状缺陷且晶片缺陷数量多,团状缺陷主要发生在刻蚀工艺和光刻工艺,可检查各工艺步骤,通过实验排除法确定缺陷来源。根据缺陷模式比值比,团状缺陷模式对晶圆受缺陷限制的成品率影响最大,晶片缺陷数量每增加一单位,缺陷失效概率增加4.27,其次为线性缺陷模式、环状缺陷模式与粒子缺陷模式。晶圆特征尺寸与受缺陷限制的成品率呈负相关,即晶圆特征尺寸越小,对缺陷控制要求越高。
5 结 论
基于缺陷计量数据构建晶片失效概率模型,进而预测成品率。首先采用基于噪声的密度聚类算法对缺陷点聚类,获得缺陷模式;考虑缺陷聚集性与缺陷数据的嵌套结构,构建HL模型预测晶片失效概率。该模型考虑了晶片水平更加具体的信息,违背了更少的Logit回归模型的假设,具有更高的预测精度。同时考虑了产品层与个体层的交互效应,可适用于不同产品的混合预测。
下一阶段研究可以考虑更多的影响因素提高模型的预测能力,如缺陷大小、缺陷类型等,并针对各缺陷模式对成品率影响进行更深入的研究,提出指导半导体生产线加工与调度决策的可行性策略,提高芯片质量,降低芯片成本。

