好评奖励的有限理性经济策略与演化博弈分析
李明琨,葛艺博
(上海大学 管理学院,上海 200444)
随着互联网快速的发展,电子商务作为新型的商业运作渠道,逐渐颠覆传统商业营销模式。相较于商家占主导的传统信息传播形式,在虚拟的网络购物平台中消费者更倾向于利用以用户生成内容(user generated contents)为核心的评价系统进行信息交换与口碑传播。潜在消费者利用在线评论内容获取产品信息[1],降低购买风险和不确定性[2]。商家依靠评论内容促进产品销量[3],尤其是新上线产品的销量[4],以此提升知名度和品牌效应。第三方平台则根据用户评价内容对店铺进行流量管理。通过累积动态评分来判断商家的受欢迎度,并给予优秀商家更多的流量[5]。这种评价规则无疑导致卖家优者更优,劣者更劣。评论内容不仅关乎到消费者的购买决策,更关乎到商家在平台中的“存亡”。为了在激烈的市场竞争中不被淘汰,商家已不满足消费者自发的分享购物经验,而是通过推出“好评返现”、“好评返券”等新的好评奖励机制,试图刺激消费者的评论积极性,由此提高店铺的动态评分。
从营销的视角,商家可通过各种形式的奖励策略激励已有顾客将所购商品以口碑传播的形式推荐给潜在顾客[6]。好评奖励可为消费者带来优惠,为商家带来销量,为第三方平台带来点击量,因此,此类营销方式一经推出便被广泛使用。然而,消费者在奖励刺激下给出的评论信息可能存有不实的状况[7]。本应以“信任”为基础发展起来的电商市场逐渐充斥了为“挣好评”而出的虚假信息,部分评论成为变了味的推销。究其原因,有学者认为是消费者见小利而忘大义、助纣为虐导致的结果[8];也有学者将其归结于商家的逐利性[9],并站在“商业贿赂”的角度阐述卖家好评奖励行为对自身、消费者及市场造成的危害[10]。这些研究的一个基本假设前提是消费者及商家的完全经济理性,即逐利。然而,奖励对消费者撰写评论有着更为复杂的影响[11]。消费者亦可能出于对商品不尽满意后的损失厌恶及补偿心理给好评拿奖励,或是出于对平台“差评骚扰”的担忧而妥协[12]。另一方面,贿赂性好评的存在使得消费者重新审视在线评论的价值[13],越来越多消费者甚至忽略好评只关注差评,这又使得商家需斟酌使用其营销手段。
对好评奖励的研究可以从消费者的视角探讨口碑传播及消费者推荐意愿的影响因素。如张德鹏等[14]利用社会心理学,证明顾客参与对口碑推荐意愿有显著的调节作用。戴国良[15]研究发现,满减、特价、秒杀等不同促销方式对消费者口碑传播意愿有不同的作用。谢毅等[16]则认为消费者的口碑传播意向会受品牌信任和品牌情感的共同影响。以商家好评奖励行为为重点,可探讨卖方的非伦理行为及其产生的影响。如黄苏萍等[17]聚焦国内在线评论呈现极度正向偏移分布的偏差现象及形成机制,认为商家经济奖励是消费者正面评价的主要动机。同样,沈超等[18]通过仿真实验也论证了商家诱导行为会提高商品好评率,进而获得竞争优势。然而,王晓蓉等[19]研究发现奖励披露会降低消费者对产品的信任度。李研等[20]基于心理抗拒理论,也证明了被迫好评会消极影响消费者的整体满意度,并抑制其后续购买行为。
可见,在现实生活中,消费者的评论行为并不仅仅取决于对产品或服务本身的满意度,而是根据整个交易过程中的感知收益和感知成本来权衡的。消费者的好评动机可能是因为拥有了较满意的产品或服务,也可能是为了获得“额外奖励”所带来的喜悦感[21],或是出于有限理性下的损失厌恶心理[22]。电商好评奖励策略与消费者推荐行为之间可能存在动态博弈的过程。根据奖励形式的不同,好评奖励通常有现金奖励和优惠券奖励,好评奖励的效果在一定程度上取决于奖励的设计和奖励的形式[23]。对于商家而言,为激励消费者发表产品评论提供经济回报,需要考虑财务成本和产出效益[24]。相较于现金奖励,好评返券可以拉动回头客创造一定比例的二次消费[25]。对于消费者而言,返现是其更加偏爱的方式[26],然而引发的贿赂性虚假评论的争议亦更大,商家需考虑政府惩罚风险及争议的负面影响。而返券要求消费者必须进行二次消费,通常还有使用的时间、场所以及购买产品类别等方面的限制,激励效果有限。商家与消费者群体如何选择策略获得更大的收益,是一个群体不断探索和演化调整的结果。因此,本文区分好评返现与好评返券策略,进行博弈的推演及比较分析。
通过总结以往文献,消费者在线评论与商品本身的质量、消费者心理、回报收益均有一定的相关性。本文基于以往研究,综合考虑产品质量、消费者心理预期以及奖励报酬等参数,并增加平台监控及政府惩罚机制,研究基于现金奖励与优惠券奖励两种好评奖励方式对消费者推荐意愿不同程度的影响,构建商家与消费者群体的演化博弈模型。分析商家与消费者在好评奖励策略中的群体行为和发展趋势,并通过对参数进行分析,找出在不同情境下影响商家与消费者行为的主要因素。
1 博弈模型构建
1.1 基本模型描述
本文主要考虑电子商务环境下商家实施好评奖励策略对消费者推荐意愿的决策影响,可以看作是双方主体博弈的结果。因此,假设在线评论平台上,商家为激励消费者好评推荐而采取的策略集为{好评返现,好评返券},消费者可采取的决策包括“给予推荐性评语”和“不给予推荐性评语”,其策略集简称为{推荐,不推荐}。
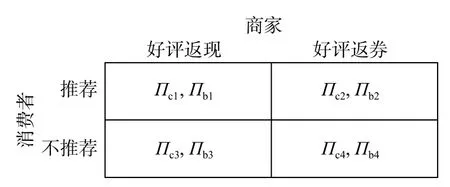
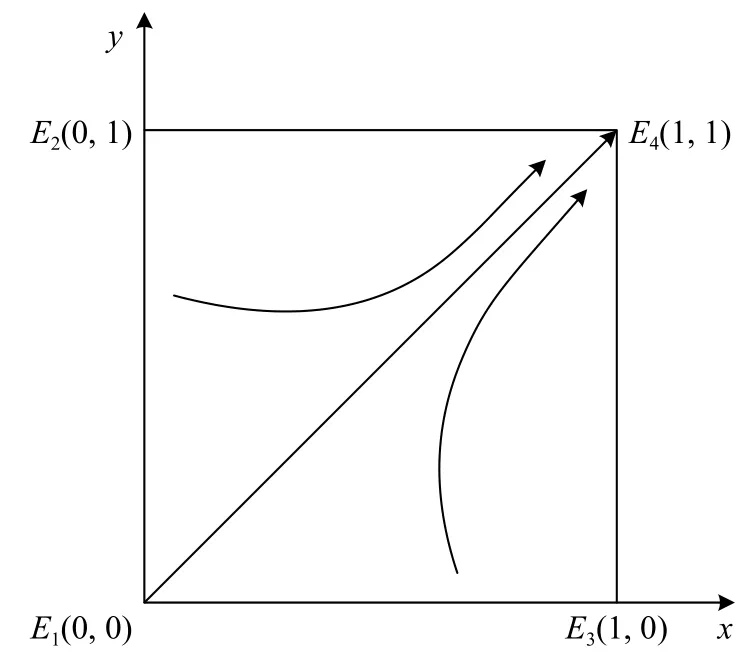
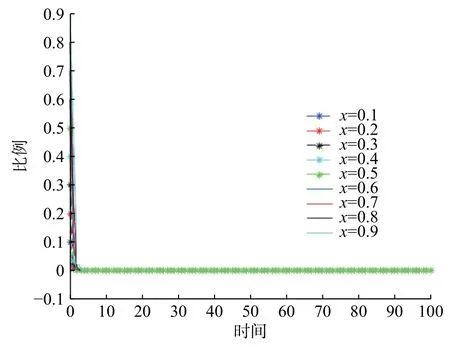
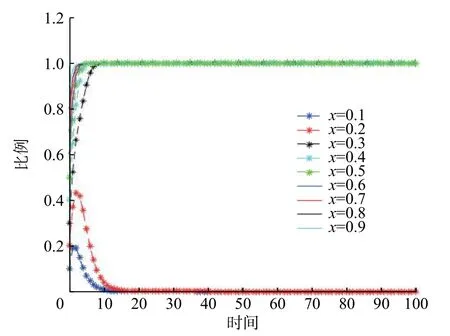
假设市场中存在商家群体以p单位的价格出售质量为q(q 一次成功的交易完成后,消费者可以选择是否进行推荐评价。假设消费者好评推荐策略能为商家带来的总潜在效益值为 λ(λ>0)。在商家承诺好评返现的前提下,消费者好评推荐可获得a单位的奖励金。在现实中,消费者如果进行非诚信推荐,要承担包括对低质量商品索赔的权益、推介的可信度、社会群体的受认可度等方面的信用代价,因此给予非诚信推荐者r1(r1>0)单位的信用惩罚。同时,商家疑似商业贿赂的行为将受到网络平台的监管和处罚,罚金为r2(r2≥0)。若满意度较高的消费者不给予推荐,意味着放弃a单位奖励金。而满意度较低的体验者不给予推荐,可以平衡较差的购物体验所带来的不满意度,从而获得f1(f1>0)单位的心理效益。商家因消费者不推荐行为损失f2(f2>0)单位的返现效益。 如果商家承诺好评赠送店铺优惠券,实施好评推荐行为的消费者将获得b单位的店铺优惠券。由于优惠券的效益在实施二次购买行为时才会生效,为分析问题方便又不失合理性,本文假设消费者若想获得优惠券收益,必须在首次消费的基础上进行多消费,用 β(0≤β≤1)表示消费者二次消费的比率。现实生活中会存在一定比例满意体验者放弃二次购买机会,假设这将损失 γb单位的优惠效益,γ(0≤γ≤1)表示消费者用优惠券二次购买商品的成本损失系数,同样会给予不诚信推荐者r1单位的信用惩罚。满意度较低的体验者不推荐行为可以平衡较差的购物体验所带来的不满意度,从而获得f1(f1>0)单位的心理效益。商家因消费者不给 予好评推荐需承担的返券效益损失为f3(f3>0)。 假定消费者购买该产品后表现为满意和不满意两种状态的概率分别为 θ 和1 −θ(0<θ<1)。消费者采取“推荐”策略的概率为x,采取“不推荐”策略的概率为 1 −x,其中,0≤x≤1;商家采取“好评返现”策略的概率为y,采取“好评返券”策略的概率为1 −y,其中,0≤y≤1。根据以上假设,构建商家与消费者博弈行为的收益矩阵,如图1所示。 图1 商家与消费者好评奖励博弈收益矩阵Fig.1 Payoff matrix of business and consumers on rewards for favorable reviews 图中,Πc,Πb分别代表消费者与商家的收益函数,不同策略行为中,消费者收益函数表达式分别为 如果消费者选择推荐策略,那么收益函数是Πc1和 Πc2。 式 (1)和 (2)之间的差异在于返券策略下要获得推荐收益需要在首次购买的基础上多消费。在不推荐策略下,消费者的损失收益值是Πc3和 Πc4唯一的区别。同样,在不同奖励策略下,商家收益函数表达式分别为 考虑到现实情况,商家给予现金奖励时容易被监管部门检测到商业贿赂性行为并受到相应的惩罚。因此,Πb1与 Πb2之间除了基础收益不同外,惩罚成本也是一项差异。 在电子商务平台中由于双方信息不对称,商家与消费者之间的行为决策很难实现完全理性。消费者个体行为的差异将导致在策略选择过程中存在部分消费者不选择完全理性博弈的均衡策略,而是通过不断地学习、模仿、试错等动态调整过程作出决策,最终达到一个稳定的均衡结果。商家也会根据好评奖励策略带来的总收益和总风险大小不断地调整策略,采取对自身最有利的行动,这与演化博弈思想一致。因此,基于复制动态的演化博弈分析方法,由图1可知,参与博弈的消费者选择“推荐”策略和“不推荐”策略的期望收益Uc1,Uc2,以及消费者平均期望收益Uc分别如下所示: 同理,参与博弈的商家选择“好评返现”策略和“好评返券”策略的期望收益Ub1,Ub2,以及商家的平均期望收益Ub分别如下所示: 假设种群中使用某一策略的个体在种群中所占比例的增长速度是该策略的相对适应性,适应度高的策略会在种群中发展。令F(x)表示消费者群体中选择“推荐”策略的复制子动态,即采用“推荐”策略的比例随时间的变化率。为便于公式书写,令 φ =(1+θγ)b+βp(θα1+θα2−α2),运用非对称复制动态演化方式,得到x的复制动态方程分别为 同理,用F(y)表示商家群体选择“好评返现”策略的复制子动态,运用非对称复制动态演化方式,得到y的复制动态方程分别为 式(15)和式(16)表明,仅当x=0,1或时,消费者选择“推荐”策略的概率是局部稳定的。仅当y=0,1或x∗=时,商家选择“好评返现”策略的概率是局部稳定的。因此,进一步 整 理 得 到 系 统 有E1(0,0),E2(0,1),E3(1,0),E4(1,1),E5(x∗,y∗) 5个局部均衡点。 本文在Friedman[27]提出的雅克比矩阵判断均衡点稳健性的基础上得到,复制动态方程可以用公式来表示。分别对x,y求偏导得到雅克比矩阵表达式为 各均衡解对应的雅克比矩阵J及其行列式Det和迹Tr如表1所示。 表1 各均衡解所对应的雅克比矩阵表达式及行列式和迹Tab.1 Jacoby matrix expressions and determinants and traces of each equilibrium solution 在本博弈中,A=f2−f3;B=f2−f3+b−a+(θ−1)r2−β(p−q);C=(1−θ)(r1+f1)−φ;D=(1+θ)a−φ。 以往很多研究都指出,与优惠券相比,现金奖励更能激起消费者的推荐意愿[28]。如果商家采取返现奖励策略所需承担的成本及损失低于返券奖励策略,即当参数满足条件: 这 时 系 统 中 存 在4个 均 衡 点E1(0,0),E2(0,1),E3(1,0),E4(1,1)。 并且A<0,B>0,C<0,D>0。将均衡条件代入表1中,E4(1,1)是该条件下的演化稳定策略,如图2所示。商家普遍趋向于“返现”策略,消费者则在现金的诱导下均实施“推荐”行为。 图2 A <0,B>0,C <0,D>0时均衡解的复制相位图Fig. 2 Phase diagram of the equilibrium solution when A<0 , B>0,C<0,D>0 然而对于商家来说,实施现金奖励通常比实施优惠券奖励所承担的运营风险更高[29],即当参数满足条件: 系 统 中 存 在E1(0,0),E2(0,1),E3(1,0),E4(1,1),E5(x∗,y∗)5 个均衡点。在这种条件下,B 图3 B 除以上情景外,有学者从心理账户的角度认为“好评返现”往往比“好评返券”更容易引起消费者的疼痛感[30]。尤其对不满意度较高的正直消费者来说,当发现收到的商品与评论不符时,便会认为所谓的“好评”都是商家花钱买来的,更加会激起这类消费者的报复心理。他们会放弃获得奖励的机会,不发表评论,甚至用更差的言论来拒绝给予商品推荐。在这种背景下,返现给商家带来的损失f2大 于返券给商家带来的损失f3,当参数满足条件: 如图4所示,系统中存在4个均衡点E1(0,0),E2(0,1),E3(1,0),E4(1,1)。其中,均衡点(0,0)的DetJ>0,TrJ<0为该条件下的稳定均衡解。均衡点 (0,1)和 (1,0)的 DetJ<0,均 衡 点 (1,1)的TrJ>0,所以这3个均衡点均不稳定。最终的演化策略为商家“好评返券”,消费者“不推荐”。这种均衡策略对商家来说没有任何意义。 图4 A >0,B<0,C >0, D <0时均衡解的复制相位图Fig.4 Phase diagram of the equilibrium solution when A>0,B<0,C>0,D<0 基于现实情况从商家的角度考虑,当参数关系满足条件: 从消费者的角度考虑,当复制动态方程参数满足: 演化稳定路径如图5所示,系统中同时存在两个稳定均衡点分别为E1(0,0)和E4(1,1)。E2(0,1)和E3(1,0)是 不稳定的均衡点,而E5(x∗,y∗)是该状态下系统的不稳定鞍点。将商家与消费者所满足的参数条件同时代入表1中,利用雅克比矩阵判断出的演化路径与此一致。由此得知,商家与消费者最终的演化稳定状态还取决于二者不同的初始状态及环境。 图5 B >A>0, D >C>0时均衡解的复制相位图Fig.5 Phase diagram of the equilibrium solution when B>A>0,D>C>0 通过以上分析可以看出:商品的价格、成本、奖励额度、消费者不推荐时带来的负面效益值、政府监控及平台惩罚成本等均会对商家群体最终的稳定均衡状态产生影响;而产品体验满意概率、奖励收益、信用成本等均会影响消费者最终的策略选择。以下所有分析讨论均建立在条件(20)和 ( 21)的基础之上。 当参数满足条件 (20)和 (21)时,系统进入局部稳定状态,收敛于(0,0)或 ( 1,1)。 对商家来说,(1,1)点是帕累托最优均衡点, (0,0)点是帕累托劣均衡点。其演化方向取决于图5所示的面积SΔE1E2E3与SΔE2E3E4的 大小。当SΔE1E2E3>SΔE2E3E4时,商家群体选择“好评返券”的概率大于选择“好评返现”的概率,消费者群体选择“不推荐”的概率大于选择“推荐”的概率。当SΔE1E2E3 接下来根据情景对商家损失值f2,f3,消费者信用成本r1,商家惩罚风险r2这4个参数进行分析,讨论其对系统演化路径的影响。 某种新品刚上市时,急切需要消费者的口碑宣传来为其打开市场。如果消费者不支持推荐会严重影响新品未来的销售市场,相对于占据一定市场份额的畅销品来说,对商家造成的损失更大。随着新品上市时间的增加,商品的销量及评论数量趋于稳定,消费者不推荐策略对商品的影响逐渐降低,商家损失值f2或f3也会逐渐减小。当参数满足条件( 20)和 (21)时易知: 随着f2的 逐渐减小,SΔE2E3E4逐渐增大,鞍点E5会 逐渐向( 0,0)点靠近。最终商家选择“返现”的概率越来越大,消费者选择“推荐”的可能性越来越大,系统向理想的均衡状态E4(1,1)收敛的可能性较大。 随着f3的 逐渐减小,SΔE2E3E4逐渐减小,鞍点E5会 逐渐向( 1,1)点靠近。最终商家选择“返券”的概率越来越大,消费者选择“不推荐”的可能性越来越大,系统向理想的均衡状态E4(1,1)收敛的可能性较小。 消费者在进行不诚信推荐时要承担一定的信用惩罚。这些损失包括消费者对不满意商品索赔的权益、其评价的可信度、社会群体的受认可度等。面积SΔE2E3E4对不诚信消费者信用惩罚成本求导得 面积SΔE2E3E4是消费者信用惩罚成本的减函数。社会信用体系给予不诚信推荐者信用惩罚越大,区域面积SΔE2E3E4越小,消费者选择推荐策略的概率逐渐减小。 商家采取好评返现策略往往要面临较高的政府或平台的惩罚风险。随着政府对电子商务市场诚信环境监管力度的大力提升,平台也发布评价新规,禁止商家实施非法好评返现策略。 面积SΔE2E3E4是商家受政府及平台惩罚风险的减函数,随着政府惩罚力度的增强,商家采取好评返现需要承担的风险成本越来越高,区域面积SΔE2E3E4逐渐减小。商家群体的期望利润降低,返现能力不足,进而采取好评返券激励策略的概率逐渐增大。此时,消费者因商家返券而改变自己推荐意愿的可能性并不大,依旧按照自己的满意度进行推荐与否的策略选择。这种情况下产生的评论更具有信度,对电商市场而言,这种返券激励不失为好的营销手段。 以上数学分析证实了在不同情境下,商家损失值、消费者信用成本以及商家惩罚风险都会影响博弈双方最终策略的选择。有学者认为,消费者对购物体验的满意度是促使其发表在线评论的主要影响因素[20,31]。而基于本文的研究内容,在不同种类好评奖励的刺激下,消费者对商品本身的满意度对其推荐意愿的影响作用如何,需要进一步讨论。 为了更加直观清晰地了解均衡状态的演化过程,本文运用Matlab软件求解消费者对商品本身满意度偏低、对商品本身满意度适中、对商品本身满意度较高3种情形下商家采取好评返现和好评返券两种不同策略倾向对消费者推荐意愿的影响。通过变动参数范围进行数值仿真,直观分析θ在不同初始状态下商家及消费者策略选择的演化路径。 前期已为 θ赋值多组数据进行仿真实验,为了更加明显地展示出演化路径,本文选取仿真效果最明显的一组参数:θ=0.3,θ=0.5,θ=0.7,分别作为消费者对商品本身满意度偏低、对商品本身满意度适中、对商品本身满意度较高3种情形的概率。 为模拟商家奖励策略与消费者推荐策略的动态演化过程,所有参数赋值均大于零且满足条件(20)与(21),即f2−f3>0,b−β(p−q)>a+(1−θ)r2,(1+θ)a>(1−θ)f1>φ>0。模型中的其他相关参 数 及 初 始 赋 值 为a=5,b=8,p=120,q=100,β=0.1,γ=0.1,α1=0.1,α2= 0.9,r1=5,r2=1,f2=5,f3=3。 假定消费者对商品本身满意的概率 θ=0.3,为满足条件(20)与条件(21),f1取值为2。商家初始返现的概率y=0.3y=0.3时,消费者不同初始推荐概率随时间变化的动态演化过程如图6所示。在这种情境中,消费者对商品本身的感知性价比较低,随着时间的增长消费者趋于理性,商家采取返券策略很难达到激励消费者给予推荐甚至进行二次购买的目的。因此,无论初始推荐概率x为多大,最终消费者群体均会倾向于“不推荐”策略。 图6 消费者对商品满意度为0.3且商家初始返现概率为0.3时的演化路径Fig. 6 Evolution path for consumer satisfaction of 0.3 and merchant's initial cashback probability of 0.3 当商家初始返现的概率y=0.7时,消费者不同初始推荐概率随时间变化的动态演化过程如图7所示。由图7可知,x的临界值位于0.8~0.9之间。当消费者对该商品的初始推荐概率x大于临界值时,最终的演化状态为1,即消费者最终都会选择“推荐”策略。当消费者对该商品的初始推荐概率小于临界值时,最终演化状态为0,即消费者最终都会选择“不推荐”策略。由此说明,即便消费者对商品本身的感知性价比不高,只要商家初始返现概率足够大,便有机会使消费者做出“推荐”策略。消费者愿意用现金收益弥补商品本身给自己带来的损失。 图7 消费者对商品满意度为0.3且商家初始返现概率为0.7时的演化路径Fig.7 Evolution path for consumer’s satisfaction of 0.3 and merchant's initial cashback probability of 0.7 假定消费者对商品本身满意的概率 θ=0.5,为满足条件 (20)与 条件 (21),f1取值为5.3。商家初始返现的概率y=0.3时,消费者不同初始推荐概率随时间变化的演化过程如图8所示。在这种情境中,x的临界值位于0.8~0.9之间。消费者对该商品的初始推荐概率x大于该临界值时,最终的演化状态为1,即消费者最终都会选择“推荐”策略,当消费者对该商品的初始推荐概率小于临界值时,最终收敛于0,即消费者最终都会选择“不推荐”策略。这说明消费者对商品本身感知性价比适中时,商家普遍采取返券策略对消费者的激励效果并不显著。 图8 消费者对商品满意度为0.5且商家初始返现概率为0.3时的演化路径Fig. 8 Evolution path for consumer satisfaction of 0.5 and merchant's initial cashback probability of 0.3 当商家初始返现的概率y=0.7时,消费者不同初始推荐概率随时间变化的动态演化过程如图9所示。由图9可知,x的临界值位于0.4~0.5之间。在现金奖励的激励下,消费者对该商品的初始推荐概率x大于临界值时,最终的演化状态为1,即消费者最终都会选择“推荐”策略,消费者对该商品的初始推荐概率小于临界值时,最终演化状态为0,即消费者更倾向于按照自己最初的意愿进行评价。 图9 消费者对商品满意度为0.5且商家初始返现概率为0.7时的演化路径Fig. 9 Evolution path for consumer satisfaction of 0.5 and merchant's initial cashback probability of 0.7 假定消费者对商品本身满意的概率 θ=0.7,为满足条件 (20)与 条件 (21),f1取值为17。商家初始返现的概率y=0.3时,消费者不同初始推荐概率随时间变化的演化过程如图10所示。由图10可知,x的临界值位于0.6~0.7之间。消费者对该商品的初始推荐概率x大于该临界值时,最终的演化状态为1,即消费者最终都会选择“推荐”策略。当消费者对该商品的初始推荐概率小于该临界值时,最终收敛于0,即消费者最终都会选择“不推荐”策略。在这种情境中,消费者对商品本身的感知性价比较高,即使初始返现概率不高,消费者依旧愿意给予推荐。 图10 消费者对商品满意度为0.7且商家初始返现概率为0.3时的演化路径Fig. 10 Evolution path for consumer satisfaction of 0.7 and merchant's initial cashback probability of 0.3 当商家初始返现的概率y=0.7时,消费者不同初始推荐概率随时间变化的动态演化过程如图11所示。消费者初始推荐概率x的临界值位于0.2~0.3之间。消费者对该商品的初始推荐概率x大于该临界值时,最终的演化状态为1,即消费者最终都会选择“推荐”策略;消费者对该商品的初始推荐概率小于该临界值时,最终演化状态为0,即消费者更倾向于按照自己最初的意愿给予评价。这种情况下,消费者对商品本身的感知性价比较高,商家又在高概率下采取直接返还现金的激励策略,消费者很容易便会达到“推荐”状态下的稳定均衡。 图11 消费者对商品满意度为0.7且商家初始返现概率为0.7时的演化路径Fig. 11 Evolution path for consumer satisfaction of 0.7 and merchant's initial cashback probability of 0.7 观察图6~11可知,在其他参数一定的情况下,消费者初始推荐概率x大于临界值时,收敛速度会随着初始推荐概率的增大而逐渐加快,使其更加迅速地收敛于 (1,1)点 。当初始推荐概率x小于临界值时,收敛速度随着初始推荐概率的减小而逐渐加快,初始推荐概率越小,收敛于 (0,0)点的速度越快。此外,消费者是否给予商品推荐不仅取决于初始推荐概率的大小,还与对商品本身性价比的满意度及商家返现概率大小有关。横向对比图6和图7、图8和图9、图10和图11便可以发现,当消费者对商品本身满意的概率处于同一水平时,仅考虑返现与返券两种激励策略,商家群体更高概率的返现行为比更高概率的返券行为更能激励消费者进行推荐。纵向对比图6、图8与图10(或图7、图9与图11)发现,当商家返现(或返券)概率一定时,消费者对商品本身满意的概率值θ越高,x临界值就越低,系统越容易收敛于(1,1)点,消费者选择推荐策略的可能性也就越大。 在网络购物市场中,好评奖励策略被良莠不齐的商家广泛使用,使当前在线评论系统受到严重挑战,也给网络购物的市场反馈与信用评价体系带来较大争议。本文在有限理性假设的基础上,将商家及消费者信用成本融入到演化博弈的收益矩阵中,考虑了商品本身对消费者的影响及商家奖励对消费者行为的影响。通过分析不同情境下商家的策略选择及消费者的行为演化情况,并分析不同情境下参数变化对演化过程的影响,得到以下主要结论: a.商家的策略选择取决于商品的销售利润、奖励成本、消费者不推荐时带来的负面效益值、政府监控及平台惩罚成本的综合收益。商家的初始返现概率对消费者的推荐概率也有显著的影响。而消费者最终的推荐行为与信用成本,奖励额度、对商品本身的满意度等参数有关。相对于商家奖励,消费者更加重视自己对商品本身的满意度。 b.消费者不诚信评价获得的返现净收益随着信用成本的增加而减少。这些信用成本包括消费者对不满意商品索赔的权益、其评价的可信度、社会群体的受认可度等。若社会信用体系的建设使消费者必须付出这些代价去获取一些金钱回报,将大大降低其不诚信推荐的意愿,有利于抵制贿赂性推荐奖励的发生。 c.政府或网络平台对商家信用监管的重视,会使得商家以金钱奖励换好评的贿赂性行为代价增加,而商家期望利润的减少会进一步降低其提供返现的能力。因此,针对非诚信评价行为,政府或平台对商家的监管与惩罚有利于遏制或减少贿赂性奖励行为的发生。 d.通过实验分析可得,商品本身性价比较高,导致消费者初始满意概率较大时(例如满意度θ=0.7),商家好评奖励不失为一种有效的营销手段。实施奖励行为不仅可以增加商家自身收益,还可以激励消费者积极为潜在顾客提供参考意见。但如果销售的是低质量产品,消费者初始满意度只有θ=0.3,给予推荐评论的可能性很小,商家难以采用返券策略来激发消费者的二次购买,必须提高返现率才可能买来一些“好评”推荐,此时的好评奖励便成为商业贿赂行为。因此,在实践中,商家要想更好地利用好评奖励,应当首先保障自身产品能给顾客带来较高的满意度,不宜单纯依靠奖励来刺激消费者进行好评推荐。在消费者对产品本身满意概率较高的情况下,好评奖励手段更多体现为激发消费者的推荐评价意愿,获取更多有实质内容的店铺评价信息。而在消费者对产品不满意情况下,以奖励换推荐的行为可能会适得其反,使消费者更不信任店铺评价内容,更不愿意进行非诚信推荐。 本研究将商家和消费者的信用成本及平台的奖惩机制融入到演化博弈的收益矩阵中,改变以往仅聚焦于在线评论本身或商家贿赂行为的研究思路,将研究视角转向商家与消费者两者间的博弈行为,为后续相关研究提供新的角度。例如可加入新的博弈方,构建商家、消费者、第三方平台间的三方博弈模型,利用演化路径系统地分析监管及惩罚机制在好评奖励中所起的作用。1.2 收益矩阵的构建

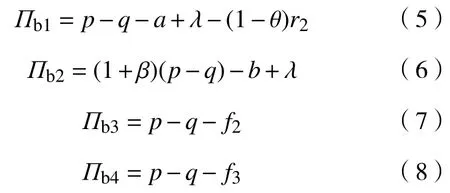
1.3 动态方程求解


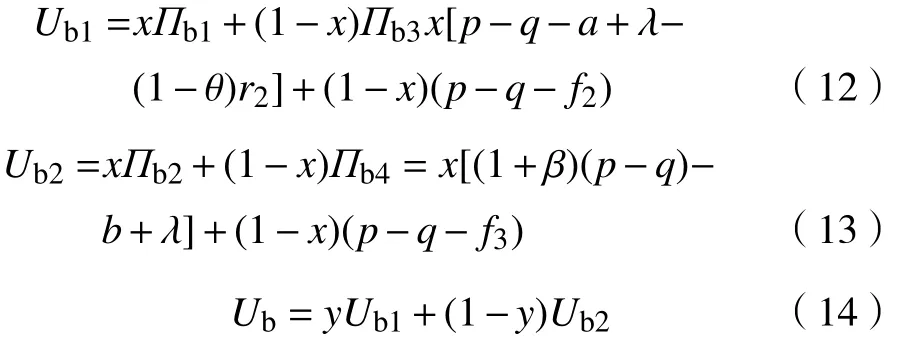




1.4 模型稳定性分析








2 演化博弈分析

2.1 不推荐给商家造成的损失


2.2 风险成本

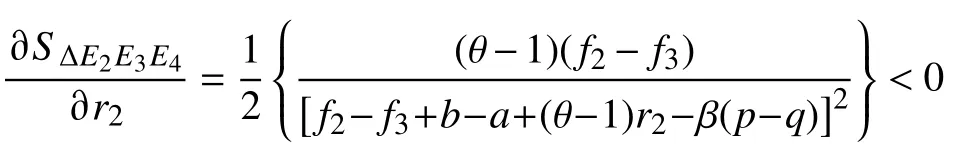
3 数值仿真
3.1 消费者对商品本身满意度偏低

3.2 消费者对商品本身满意度适中


3.3 消费者对商品本身满意度较高

4 结 论

