应用模拟退火算法进行电动汽车转向传动比的 设计研究*
牛 晶
(天水师范学院机电与汽车工程学院,甘肃 天水 741001)
引言
主动前轮转向技术(AFS)是先进辅助驾驶系统很重要的一个方面,影响汽车的主动安全[1-3]。基于分布式4WD电驱动底盘结构的主动前轮转向技术更易于实现车辆的驱动防滑和制动防抱死,能有效地提高车辆的操纵稳定性[4]。
这种转向系统一般集成在电动助力转向系统(EPS)上,通过助力电机和双行星齿轮机构执行前轮附加转角控制,实现车辆循迹、主动避障和提高车辆的横摆稳定性。现阶段,国内外对AFS研究的核心问题主要集中在前轮附加转角应当基于何种规律施加控制,而这是决定转向品质的关键[5-7]。传统转向系统中,转向系的传动比是定值,会导致车辆低速工况下转向费力,轻便性差,而高速工况下,转向灵敏性差,无法同时满足车辆在不同工况下对转向灵敏性和轻便性的双向需求。
为此,本文基于分布式4WD电驱动汽车底盘结构参数建立了三自由度非线性前轮主动转向动力学模型;考虑影响转向传动比的工况因素,设计了采用固定横摆角速度增益和固定侧向加速度增益可变权重共同控制的理想传动比规律;应用模拟退火算法(SA)对控制参数进行了动态优化;最后,通过仿真实验对比了理想传动比规律下车辆响应与固定传动比车辆响应,为今后分布式4WD电驱动底盘主动前轮转向系统的设计与开发提供了一定的理论基础。
1 三自由度非线性前轮转向动力学模型
1.1 前轮角输入至整车横摆输出的两轮模型
假设车辆在前轮转角δf输入下作圆周运动,建立如图1所示的转向动力学模型。图1中,车速V,在车辆质心处分解为沿x轴的分量Vx和沿y轴的分量Vy,质心侧偏角β,轮距B,轴距L,前后轮驱动力Fxk(k=1,2分别代表前、后轮),前后轮侧向力Fyk。前后轮驱动力Fxk由驾驶员通过油门踏板由轮毂电机驱动力矩控制。
为了方便研究,忽略次要因素,作如下假设:
1)忽略空气阻力的作用;
2)忽略悬架的作用,只考虑车辆的平面运动和由路面不平引起的垂向运动;
3)车辆前后轮的侧偏特性一致;
4)车辆纵向速度保持不变。
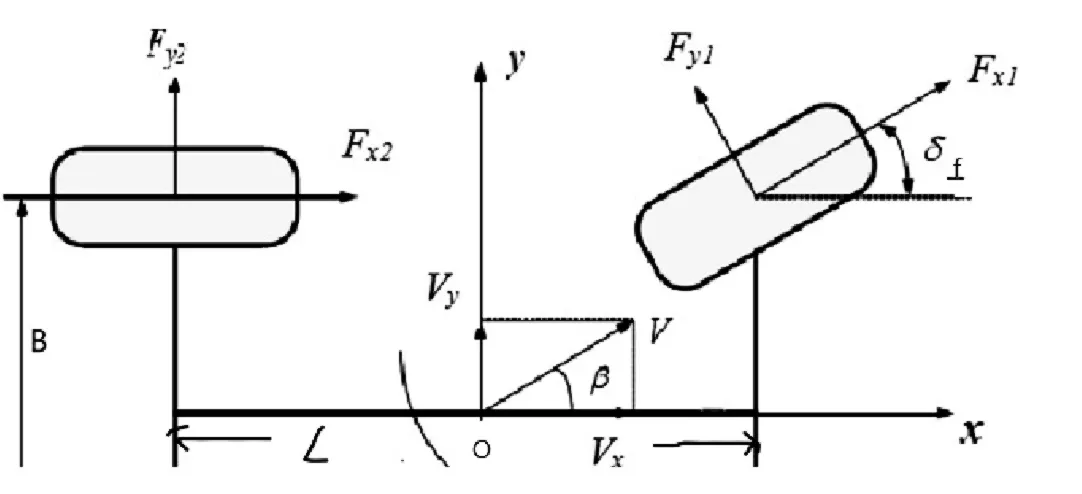
图1 车辆两轮转向模型
根据实验证明,轮胎与地面之间作用的侧向力Fyk是一个非线性力,其大小受侧偏角影响[8]。文中采用郭孔辉院士提出的“统一模型”[9]建立Fyk(α)与侧偏角α的关系,其中忽略纵向滑移的存在,模型如式(1)(2)所示:

式中,α是轮胎侧偏角,Fzk是前后轮的法向载荷,ky是轮胎的侧偏刚度,μ是轮胎的摩擦系数,E是轮胎材料的弹性模量,质心距离前轴中心a,质心距离后轴中心b。
实验对象整车主要参数详见下表1。
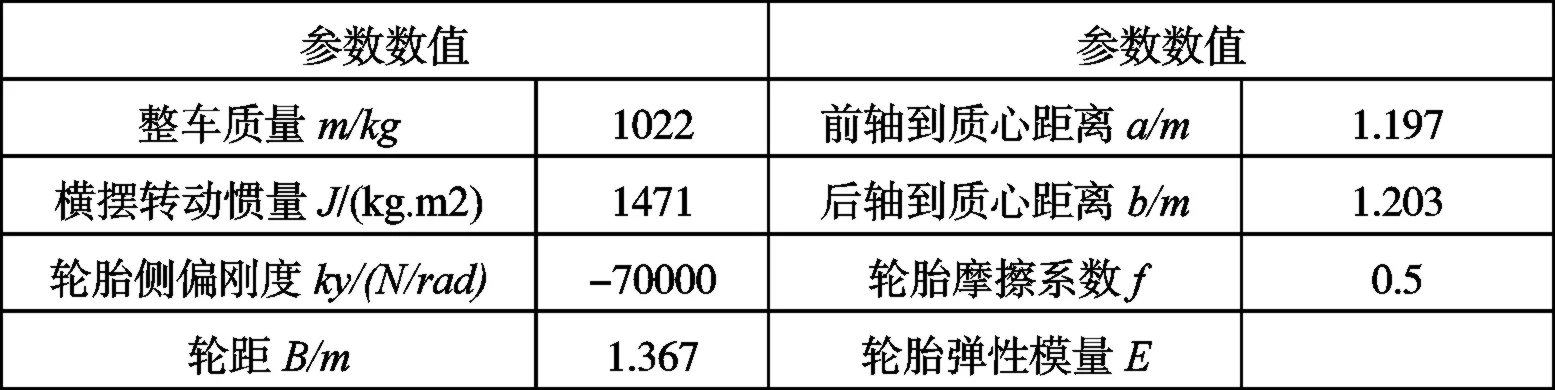
表1 某分布式4WD纯电动汽车主要参数
根据达朗伯原理,建立车辆三自由度非线性动力学方程如下:
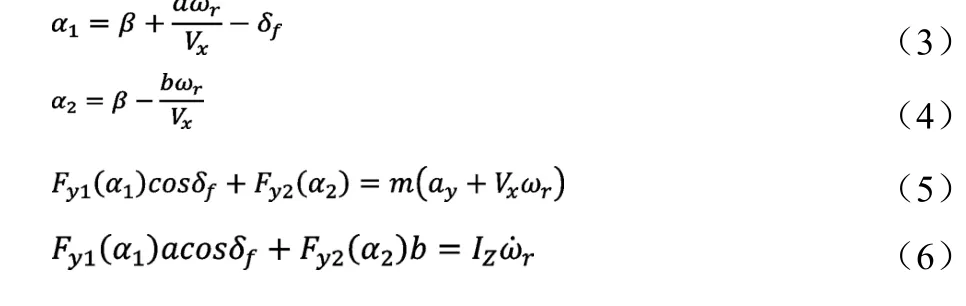

式中,α1、α2分别是前后轮的侧偏角,IZ是整车绕Z轴的转动惯量,ωr是车辆质心处的横摆角速度,ay是车辆质心处的侧向加速度。
1.2 转向盘角输入至前轮角输入模型
本文研究的转向系统包括两个执行机构,即主动前轮转向执行机构(AFS)和电动助力转向执行机构(EPS)。整个转向系统包括两个电机,一个产生前轮附加转角,一个位于齿轮齿条转向器中,起助力作用,具体结果见图2。最终主动前轮的转向角由两部分叠加,即驾驶员作用在转向盘上的角输入δp和AFS机构的前轮附加转角δd组成,其中转角叠加机构为一双行星齿轮机构,见图3所示。
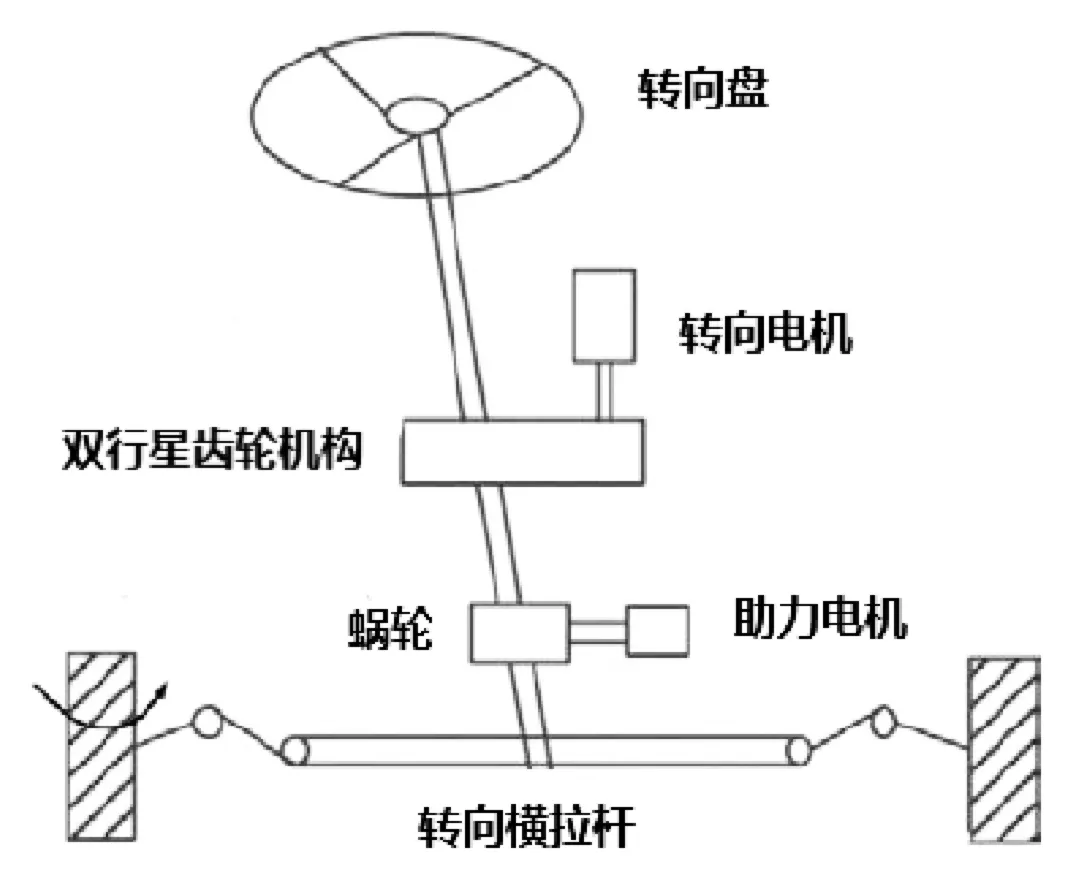
图2 转向系统机构

图3 双行星齿轮机构
文中转向盘,路感电机、转向执行电机的数学模型均建立[10-12],篇幅有限,本文不再赘述。
2 理想转向传动比控制规律
2.1 理想转向传动比的概念
对于前轮转向汽车,将转向盘转角δsw与前轮转角δf之比定义为转向传动比i,如式(8)所示:

传统汽车的转向传动比是一个定值,由汽车的结构参数决定,主要由转向器传动比和转向梯形传动比构成。这种情况下,转向特性随车速大范围变化,表现出低速情况下转向轻便性不足,高速情况下转向灵敏性不足的缺陷[13]。因此,为了改善这个缺陷,必须通过不断变化的传动比使转向特性呈现出与车速无关的固定比例关系,即满足在各种工况下汽车都具有相同的转向特性,从而减轻驾驶员的操纵负担,一般将这种变化的传动比定义为理想转向传动比。
2.2 理想转向传动比的设计
三自由度非线性车辆模型在转向盘角阶跃输入后最终将达到稳态等速圆周行驶状态。一般,常用横摆角速度增益和侧向加速度增益来衡量车辆的转向品质。通过下图4-6所示的转向仿真模型,可以得到更符合实际情况的横摆角速度增益和侧向加速度增益。


式中,P和Q是权重系数,且P+Q=1。
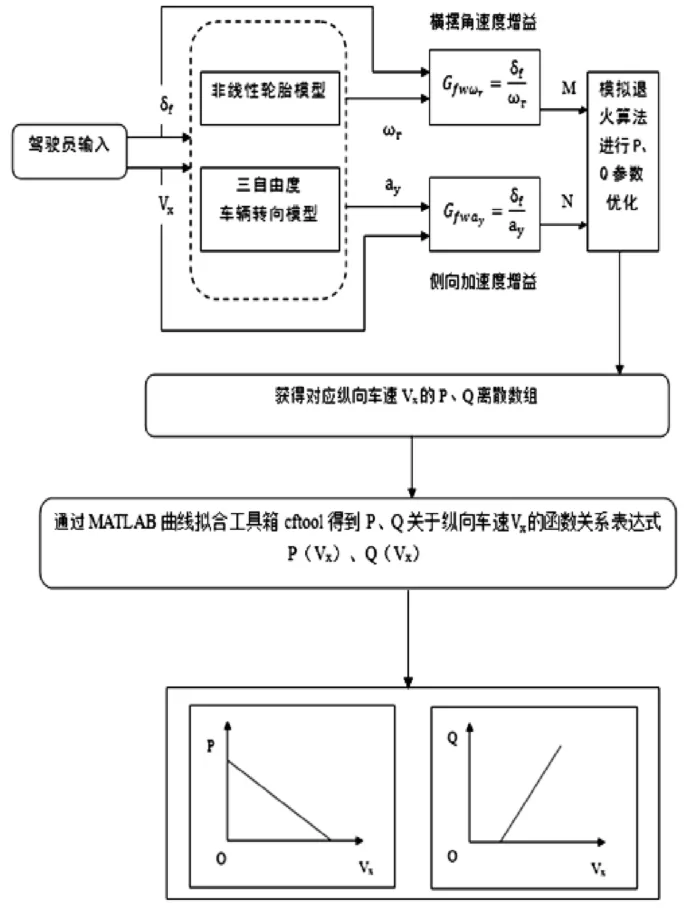
图4 转向传动比设计流程图
2.3 基于模拟退火算法(SA)求解参数P、Q
模拟退火算法(SA)是一种以得到全局最优解为目的的智能算法[16]。模拟退火算法的一般步骤是先设定初始温度T0,最低温度Tf,模型参数所涉及的定义域,目标函数。给予初始参数值一定的扰动,得到新参数组,重新代入目标函数,并将新函数值与原函数值相减得到ΔE,若ΔE<0,则新参数组被接受;若ΔE>0,则新参数组以概率被接受。在同一温度T下,重复若干次扰动后,再缓慢降低温度,直至降至最低温度Tf,停止运算,输出最优解。
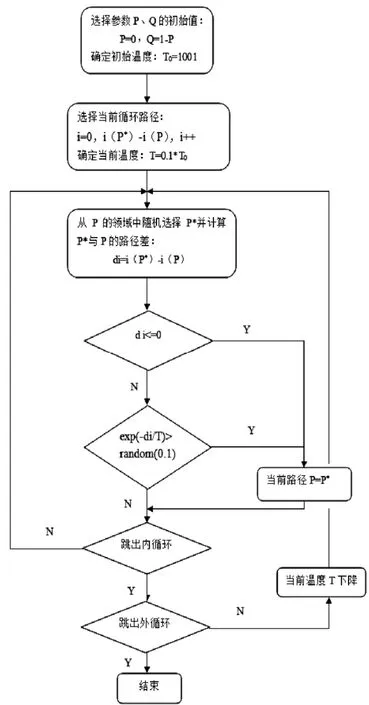
图5 模拟退火算法进行P、Q参数优化的流程图
在汽车行驶过程中,整车参数如整车质量、绕Z轴的转动惯量等一般不会变化[17]。文中求解P、Q最优值时,考虑的影响因素有两个,即车速和前轮转角。为了兼顾低速工况的转向轻便性和高速工况的转向灵敏性,采用模拟退火算法设定寻优过程中低速工况取传动比i的最大值,高速工况取传动比i的最小值[18],具体P、Q参数优化的流程如上图5所示。
文中应用CarSim/Simulink软件对某分布式4WD纯电动汽车进行了联合仿真实验。实验条件:干燥混凝土路面(附着系数0.7),无风,湿度温度适宜[19-20]。仿真工况选取:1)转向盘角阶跃输入工况30°,车速设置依次取10,20,…,100km/h;2)正弦输入模拟蛇形变道工况,幅值30°,周期5s,车速设置依次取10,20,…,100km/h。仿真得到的横摆角速度增益变化曲线和侧向加速度增益变化曲线如下图6-7所示。
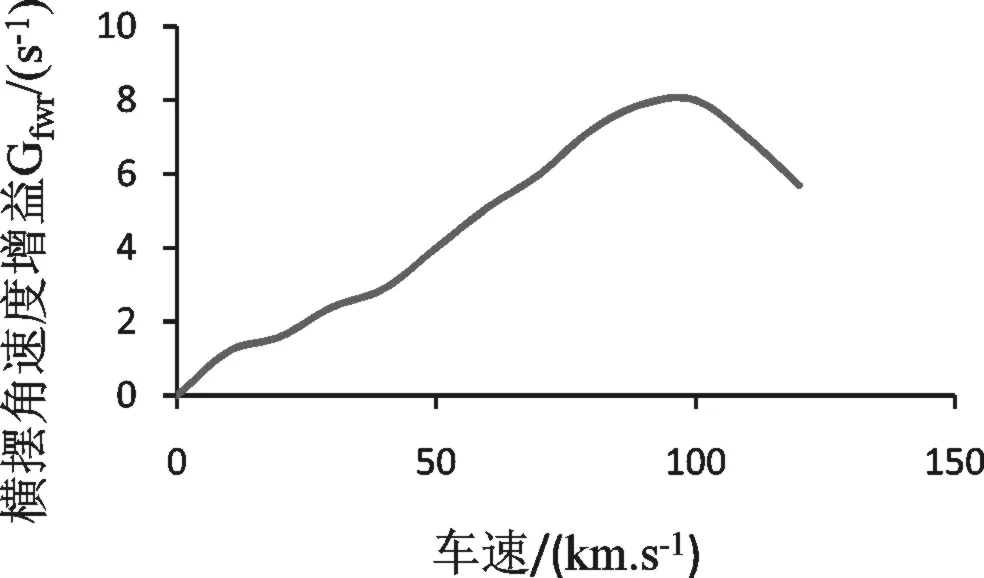
图6 横摆角速度增益曲线
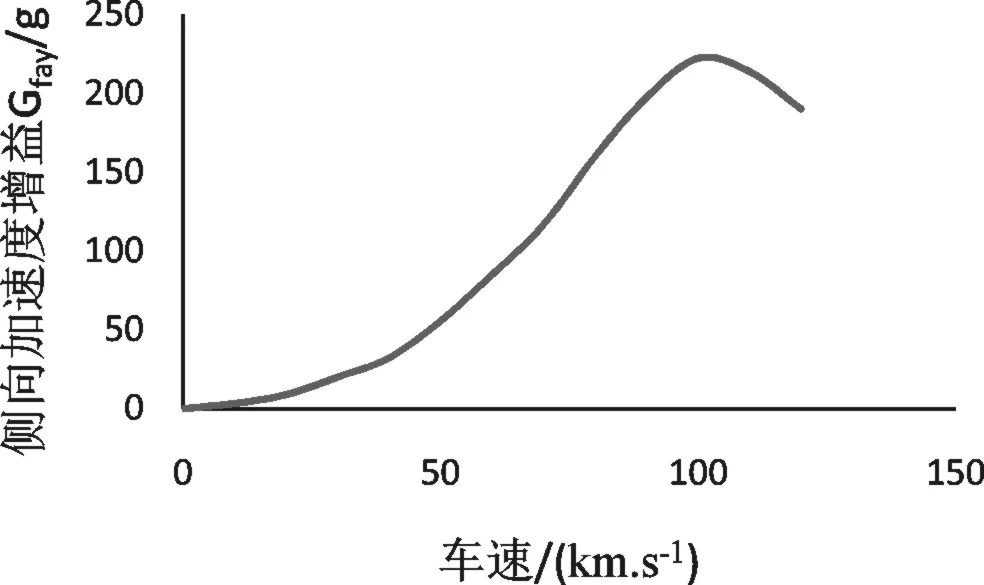
图7 侧向加速度增益曲线
采用MATLAB/Simulink软件应用SA算法编程,对高速区间不同车速的P、Q值进行优化,初始状态设置P=1,Q=0。得到正弦输入工况的某些优化结果如表2所示。
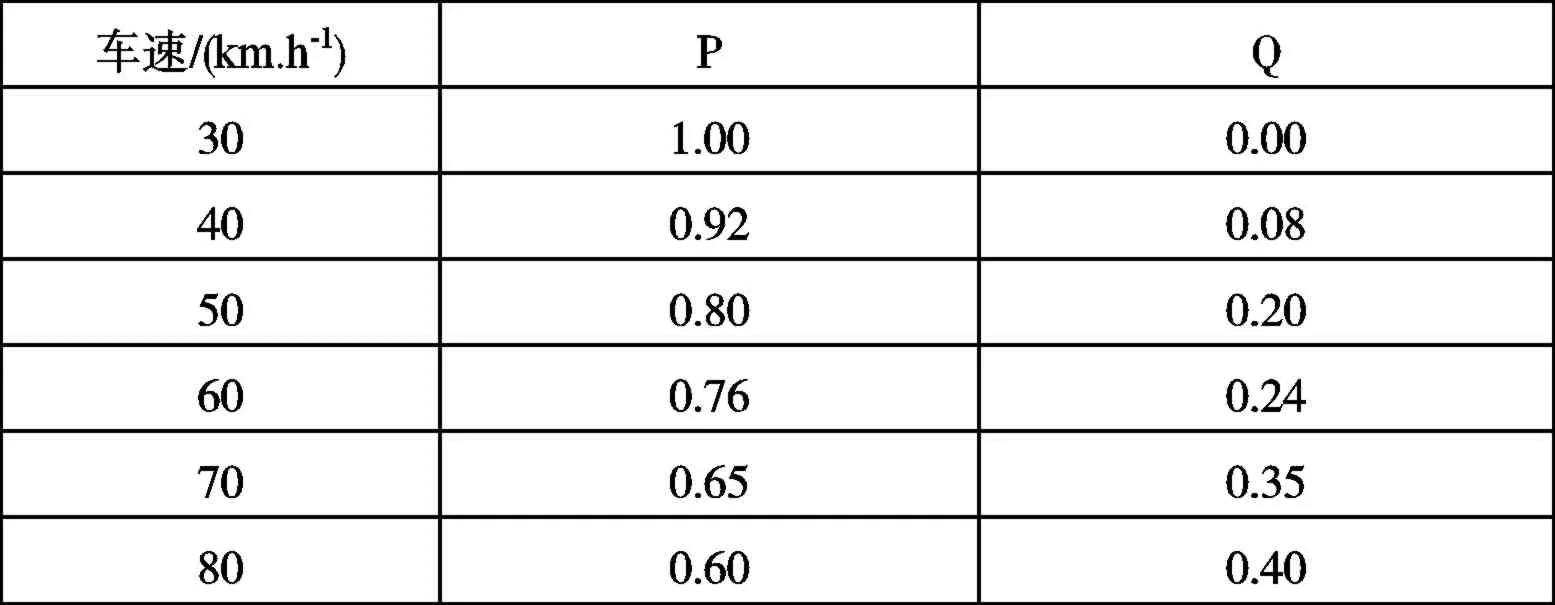
表2 部分优化实验结果
通过实验结果发现,横摆角速度增益权重系数P随着车速的增大由1减小至0.28,侧向加速度增益权重系数Q由0增大至0.72,符合车速越高对转向灵敏性需求越高的变化趋势。利用MATLAB的曲线拟合工具箱cftool分别对两个权重系数进行了函数拟合,得P=-0.008V+1.24,Q=0.008V-0.24。
3 仿真验证
为了验证四轮独立电驱动汽车SBW系统转向传动比设计的有效性和准确性,本文通过CarSim/Simulink软件联合仿真,对比了传统定值转向传动比及文中转向传动比规律下的车辆横摆响应情况。仿真过程中,选取转向盘角阶跃输入和正弦输入两种工况,路面附着系数0.7。
3.1 转向盘角阶跃输入工况
转向盘角阶跃输入下,中高速区间100km/h的仿真结果如图8-9所示。可见,文中设计的传动比变化规律可以明显减小车辆转弯过程中的横摆角速度和侧向加速度,进入稳态后,横摆角速度减小了13.6%,侧向加速度减小了23.1%。
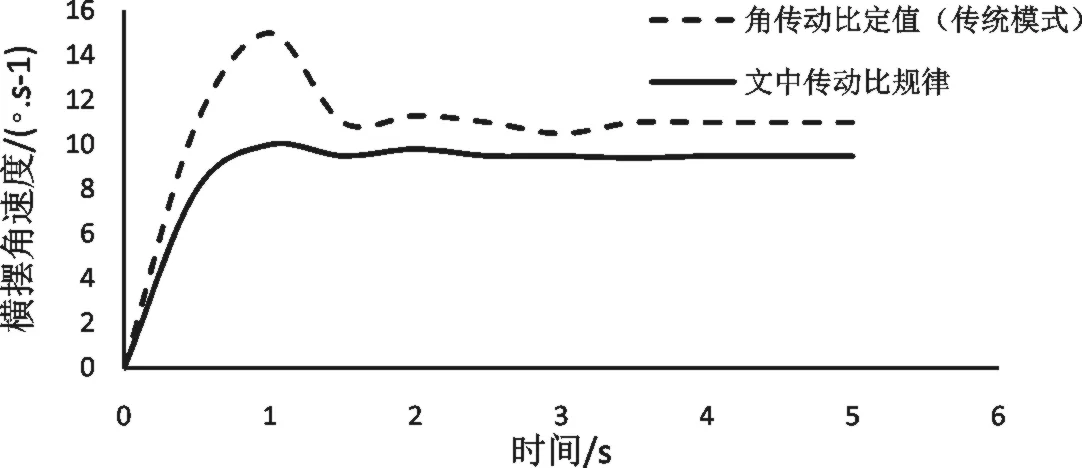
图8 车速100km/h的横摆角速度变化对比结果

图9 车速100km/h的侧向加速度变化对比结果
3.2 转向盘正弦输入模拟蛇形变道工况
转向盘正弦输入下,低速区间20km/h的仿真结果如图10所示。可见,文中设计的传动比变化规律可以明显减小车辆转弯过程中的方向盘转角幅值,幅值减小了53.5%。
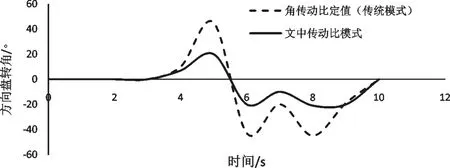
图10 车速20km/h的转向盘转角变化对比结果
4 结语
①本文基于实车数据建立了多工况的非线性CarSim/ Simulink联合仿真模型,并应用模拟退火算法对车辆理想传动比计算公式进行了动态参数优化,为今后纯电驱动前轮转向汽车的系统设计奠定了一定的理论基础;
②多工况仿真实验结果表明,所设计的转向传动比设计方法能够有效减少车辆在弯道的横摆角速度和侧向加速度,提高操纵稳定性。

