考虑储存成本的集装箱公铁联运路径优化*
徐 剑, 李周奇, 蒋 洋
(沈阳工业大学 管理学院, 沈阳 110870)
我国正逐渐步入“大交通”时代,单纯的某种运输方式已无法适应时代需求,多种运输方式联合运输越来越普遍且发展迅速。其中,公铁联运是适用范围较为普遍的联运方式,将公路的灵活性、简捷方便、响应时间短等优点和铁路运输网络四通八达、覆盖面积大、稳定性高、运量大等优势相结合,更好地实现了连续一体化运输。集装箱货运是把货物组合以集装箱作为作业单元的一种运输方式,其优点是可以降低成本、提高作业效率,保障多式联运的顺利进行。目前集装箱货运进入了前所未有的发展与完善时期[1]。集装箱公铁联运可将公路和铁路货物整体运输有机组合,减少不必要的浪费、优化作业流程、实现优势资源互补,使公铁联运效益最优化[2]。
集装箱公铁联运是内陆集装箱多式联运的主要组成部分,不同的运输路径及运输方式会产生不同的运输效率和效益。为了达到提升集装箱公铁联运体系效率和改善不合理运输方式的目的,在高效协调公路、铁路运输衔接方式的前提下,应进行合理的运输组合模式选择,使联运经营人得到最优路径,降低运输总成本,从而获取更高的收益。因此,加强对集装箱公铁联运货物运输方式和运输路径的优化,对提高联运企业收益有重要的现实意义[3]。
在公铁联运中的关键问题之一就是联运路径的选择(优化),即在不同因素、不同限制条件下模型的构建和算法的改进。联运路径的优化受运输费用、运输时间和环境等因素的影响[4]。在研究中,大多将运输时间或运输费用作为目标函数,如:Teng等基于国家绿色发展的背景,在运输成本中考虑碳成本因素[5];Yang等从多式联运经营者的角度出发,设计出双重优化目标模型,最大限度地减少了集装箱多式联运的总运输成本和总运输时间[6]。
一些学者考虑不同因素的约束建立模型,如:Ozdemir等提出了混合隐马尔科夫模型(HMM)以解决运输网络中的路径问题[7];Chang考虑货物交货时间对运输路径的影响,建立了路径优化模型[8];李珺等研究在不确定因素下建立混合不确定条件下的多式联运路径优化模型[9];于雪峤等以客户满意度为约束,建立模糊需求的多式联运路径优化模型[10];刘畅等考虑货物的时间成本价值建立多式联运路径选择优化模型,并用深度优先搜索的算法对路径选择优化模型进行求解[11]。
一些学者对路径优化的算法进行改进,如:熊桂武考虑模糊时间因素,建立了多式联运路径优化模型,设计了混合田口遗传算法求解算例[12];Feng等通过蚁群算法解决联运路径选择问题[13];彭勇等以班期限制为切入点建立联运路径决策模型,同时改进遗传算法对模型求解[14];蒋洋等对运输网络优化问题采用了启发式算法[15];成耀荣等设计变长符号编码机制的文化基因算法,求解多式联运路径优化问题[16];程兴群等考虑拥堵对运输时间的影响,建立了多式联运路径选择模型,并设计了基于保优策略和移民策略的遗传算法进行求解[17];张小龙等改进基于Pareto适应度的遗传算法,并对多式联运路径优化模型求解[18]。
通过对以上文献的研究发现,虽然很多学者在建立模型时考虑了运输成本和班期的限制,但他们大多忽略了在中转节点等待时产生的储存成本。在集装箱公铁联运过程中,联运经营人只有在充分考虑各个方面影响的基础上,才能选择合理的运输路径和运输方式,如忽略储存成本和时间惩罚成本的影响,其结果可能在现实中无法实现。因此,本文以节点的储存成本为切入点,在送达时间和班期限制的约束下充分考虑储存成本和时间惩罚成本,建立运输总成本最低的公铁联运路径优化模型,从而使模型更具有现实意义。
一、问题特征分析
考虑节点储存成本的集装箱公铁联运路径优化问题具有以下特征:
1. 多商品流路径优化
在集装箱公铁联运网络中,运输任务表现为商品流。由于运输企业同时承担多个运输任务,对不同客户运输任务不同,在实际运输中往往存在多商品流。每个运输任务都具有不同的运量、运输期限、发货点、收货点、运输起始时刻等。
2. 多约束的限制
随着现代企业对库存管理的要求不断提高,客户对不同货物都有约定的到达时间,希望货物能按照该时间准时到达。当货物到达时间超出约定时间时,一方面会影响客户对服务的满意程度,另一方面也会影响运输企业的口碑、信誉度等。同时,货物到达时间也受班期限制的影响。本文设置各节点的软时间窗限制,在软时间窗限制、班期限制、不同商品流对到达时间限制的多约束限制下,进行集装箱公铁联运路径优化问题研究。
3. 基于运输总成本优化模型
对于运输企业而言,运输总成本不仅是衡量企业运营状况的一个重要指标,还是企业盈利的重要因素之一。在节点作业时,不仅存在换装成本,还存在因等待最优班列出发的等待成本。本文将节点的等待成本计入运输总成本中,同时考虑节点间的运输成本、节点内的换装成本和送达时超出时间限制的时间惩罚成本。
针对以上特征,在收货时间限制、班期限制、不同商品流对到达时间限制的多约束限制下,建立由运输成本、换装成本、储存成本和时间惩罚成本构成的总成本最低的集装箱公铁联运路径优化模型。
二、问题描述及假设
1. 问题描述
某运输企业将多批不同数量的货物从不同的运输起点Oi(i=1,2,…,n)经过支线运输—干线运输—支线运输,将货物运输到各自的目的地Di(i=1,2,…,s),其网络结构如图1所示。干线运输包括枢纽节点间的运输路径及枢纽节点内的运输作业,存在公路、铁路两种运输方式;支线运输包括发货点到枢纽节点和枢纽节点到收货点的路径及枢纽节点内的运输作业,只存在公路运输方式。运输时间由运输距离和运输方式决定。节点间不同运输方式存在不同的运输距离;若两节点间某种运输方式不存在,则假设两节点间该种运输方式对应的运输距离无限大。
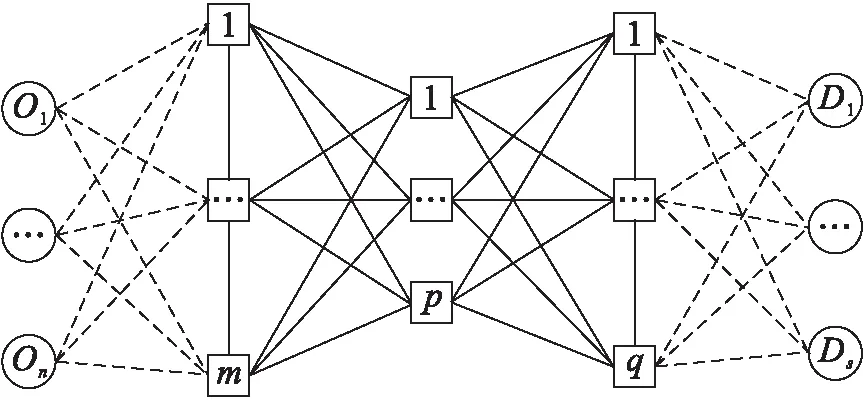
图1 公铁联运网络结构
2. 研究假设
本文基于以下假设:(1)运输任务的起讫点已知;(2)在一个运输任务内,两节点间进行运输时只能选择一种运输方式,转运只能发生在节点处,且运量不可分割;(3)同一任务在相同节点最多只能中转一次;(4)每条运输路径都有足够的能力进行运输;(5)每个中转节点都具有足够的能力实现货物中转运输;(6)火车有规定的出发时间,汽车可以随时出发。
三、模型构建
1. 模型参数及决策变量说明
模型中各参数含义如表1所示。各决策变量含义如表2所示。

表1 模型参数说明

表2 决策变量说明
2. 目标函数设计
本文研究的集装箱公铁联运路径优化问题,以运输总成本最低为优化目标。该运输总成本包括运输成本、换装成本、储存成本和超出最晚时间到达终点的时间惩罚成本。运输成本产生于不同节点采用不同运输方式进行运输的过程中;换装成本主要产生于各节点的换装作业中;储存成本产生于早到节点后等待最优班列的等待时间中;时间惩罚成本产生于货物超出最晚时间送达收货点时,和总的运输时间有重要关联。
(1) 运输成本C1。运输成本包括集装箱公铁联运网络中各种运输方式在运输路径中产生的成本,主要与运输方式的运价、运量和运输距离有关,计算公式为
(1)
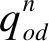
(2) 换装成本C2。在公铁联运网络中,由于运输方式和运输班列的改变都会产生换装成本,计算公式为
(2)

(3) 储存成本C3。在公铁联运网络中货物中转时,由于火车有班期限制,早到节点会产生一定的等待时间,在这期间内会产生储存成本C3,其表达式为
(3)
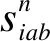
(4)
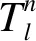
3. 约束条件分析
研究商品流公铁联运路径优化问题,既要保证每个OD流的平衡,又需考虑运输方式的连贯性。为实现对模型约束的全面刻画,建立搭乘最优班列约束、商品流约束、运输方式转换约束、中转次数约束、送达时间约束,即
(5)

(6)
(7)

(8)
(9)
式(6)、(7)共同限定每个运输任务只能对应一个起点和一个终点,保证货流不可拆分原则;式(8)保证运输方式转换顺利进行;式(9)保证每个运输任务中相邻节点只能选择一种运输方式进行运输。将式(6)~(9)相结合,确保了联运网络中各商品流通起讫点之间运输路径的唯一性和完整性,即
(10)
式(10)为节点中转约束,保证每个运输任务只能在节点i进行中转,且中转次数不超过1次,以确保运输的合理性。
(11)
式(11)保证每个运输任务在运输最晚时间前完成运输。
(12)
4. 模型表达
结合对目标函数及约束条件的分析,构建复杂约束下集装箱公铁联运路径优化模型,即
(13)
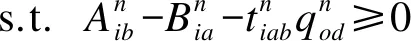

四、算例分析
现假设联运企业在零点时承担2份运输任务,以常州和无锡为起点,经南京、上海、郑州等8个枢纽节点运输到阳泉和邢台,其网络结构及节点编号如图2所示。
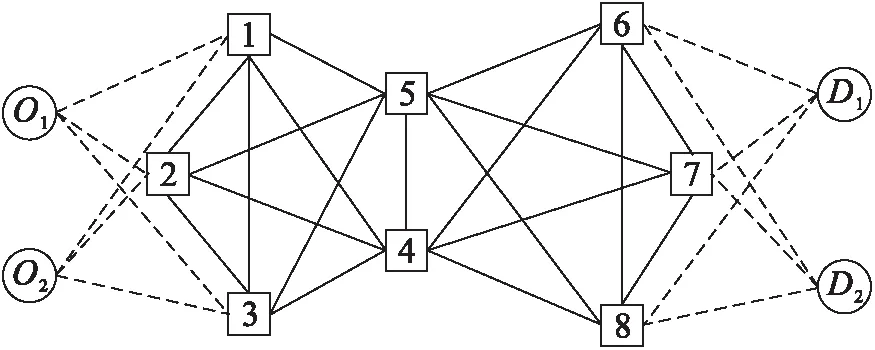
图2 公铁联运运输网络示意
要求找到运输路径和运输方式的组合使运输总成本达到最低,同时满足发货人运输时间的要求。运输任务见表3,各节点的换装具体信息和路径信息均已知。

表3 运输任务信息
根据以上信息,运用MATLAB对集装箱公铁联运路径优化模型求解。运输方式中1代表公路、2代表铁路,v1=80 km/h、v2=70 km/h;参数设计为种群规模N=80,交叉概率Pc=0.9,变异概率Pm=0.01,连续迭代100次终止运算。据此得到图3算法收敛轨迹和图4最优路径结果。
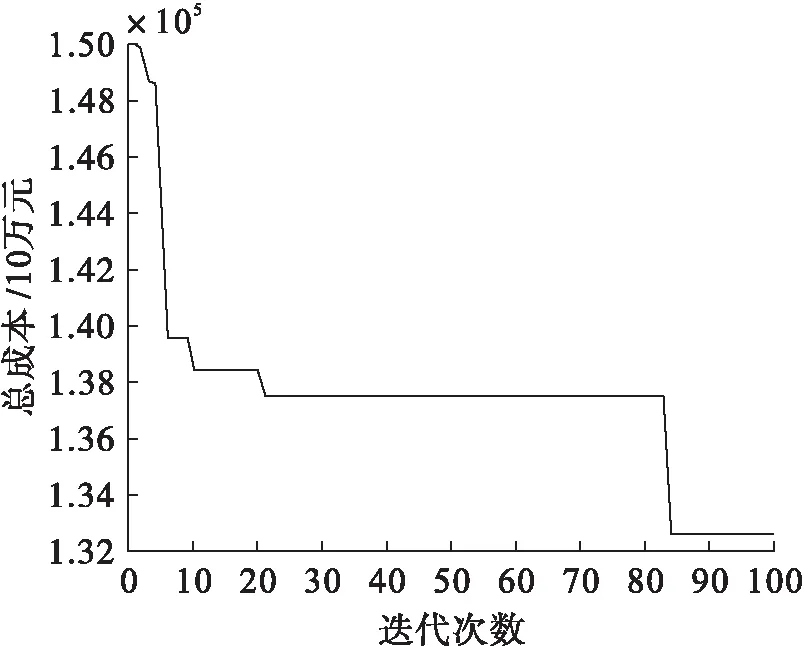
图3 算法收敛轨迹
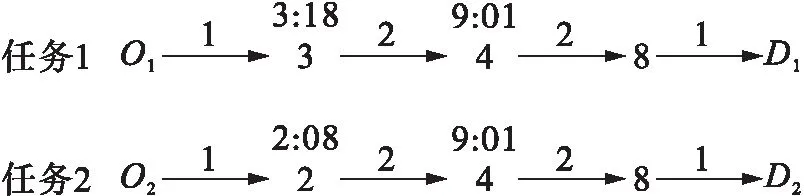
图4 最优路径结果
任务1从O1到达枢纽节点3,搭乘3∶18的火车到达枢纽节点4,经过转装等待搭乘9∶01的火车到达枢纽节点8,最终经公路运输到收货点D1;任务2从O2到达枢纽节点2,搭乘2∶08的火车运输到枢纽节点4,搭乘9∶01的火车到达枢纽节点8,最后由公路运输到达最终收货点D2。目标函数值为132 691元,其中任务1为54 507元、任务2为78 184元。
五、结 语
本文在“大交通”的时代背景下研究集装箱公铁联运路径优化问题,以节点间运输成本、节点换装及储存成本、超出最晚时间的惩罚成本构成的总运输费用为目标函数,考虑班期限制、收货时间限制建立集装箱公铁联运路径优化模型。通过算例将两个运输任务经南京、郑州等节点送到收货地,并用MATLAB软件求解得出最终的运输路径,证明了模型的有效性。

