变负载多旋翼飞行控制研究

赵 洁，陈至坤

（华北理工大学，河北 唐山063210）

1 引言

多旋翼具有很高的机动性和敏捷性，可完成悬停、垂直起飞、低速巡航等飞行任务，被广泛应用于军事侦查、灾害监测、农业植保等领域。多旋翼有六个输入、四个输出，是一个典型的欠驱动、非线性、强耦合多变量的系统，容易受外界干扰的影响[1]。因此，需要设计具有良好抗干扰能力的飞行控制策略，保证无人机能够高质量完成各种飞行任务。目前，针对多旋翼的控制问题，已经提出了一系列控制策略，文献[2]采用自适应模糊PID 对无人机的悬停姿态进行控制，实现了对悬停姿态的精确控制；文献[3]采用非线性PID 控制方法为多旋翼的轨迹跟踪问题设计了相应控制律，实现了对指定轨迹的跟踪，但是抗干扰能力较差；文献[4]设计了鲁棒正定不变集，在存在外部干扰及输入饱和约束等因素时，能够令无人机轨迹跟踪误差处于构造的不变集内；文献[5]同样设计了双环控制系统，以内模原理和高阶滑模控制为基础，引入动态面控制，能够有效实现轨迹渐进跟踪和干扰抑制；文献[6]按照级联控制的思路采用反步控制对无人机路径跟踪问题进行研究，通过姿态误差与位置误差的耦合设计了干扰观测器，从而更好地抑制了干扰；文献[7]采用串级自抗扰控制方法，进行多旋翼的悬停控制，同时引入扩张状态观测器对系统状态和内外扰动进行实时估计，鲁棒性强，实现了悬停控制，但是定点准确度较低。

为了令多旋翼飞行时具有较强的抗干扰能力，并且能够准确到达给定位置完成悬停任务，本文采用反步法设计滑模面，将反步法与滑模变结构结合设计控制器对变负载多旋翼进行控制，并与常用的串级PID 设计的控制器进行比较。仿真结果表明，反步滑模法设计的控制器较串级PID 控制器具有较强的抗干扰能力，响应速度快，定点准确度高。

2 六旋翼动力学模型

将多旋翼看成刚体，对其进行运动学和动力学分析，并进行合理简化后，得到多旋翼动力学模型如下：

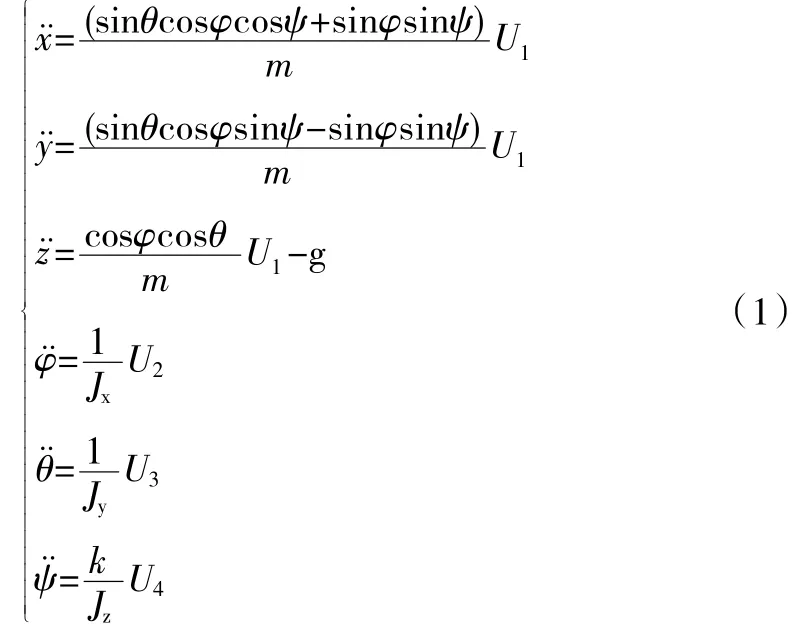
式（1） 中： （x，y，z） 为多旋翼位置坐标； （φ，θ，ψ）为多旋翼姿态角，分别表示翻滚角、俯仰角和偏航角；m 为多旋翼质量；U1、U2、U3、U4为多旋翼四个虚拟控制量，分别为总拉力、翻滚力矩、俯仰力矩和偏航力矩；g 为重力加速度；Jx、Jy、Jz为转动惯量。

在多旋翼控制器中，对于高度和偏航角的控制，是单独存在的，和其他各个分控制器之间基本没有很大联系。因为水平控制是为了得到期望俯仰角和翻滚角，而二者是姿态控制的输入量，所以，两个控制器之间联系紧密。通过数学模型推理，得到了它们之间的对应关系，再进行分析运算，得到控制器设计时需要的非线性约束条件：

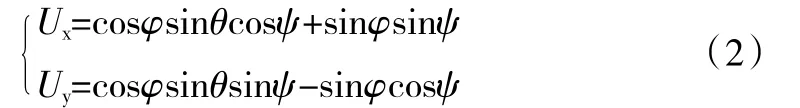
反解得到：

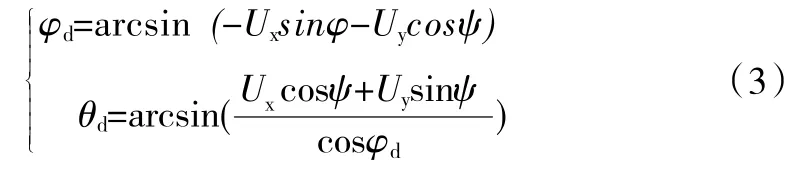
因为本文所做的定点悬停控制，是沿机头方向的飞行，没有偏航角变化，所以期望偏航角为0。所以上式可以再次简化为：

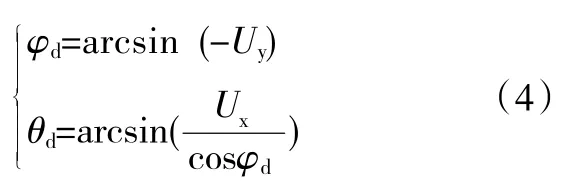
为了设计反步滑模控制律，根据反步法控制原理及特点，将多旋翼数学模型进行改写，得到符合反步法规律的反馈形式。

其中，b1=1/Jx，b2=1/Jy，b3=1/Jz，Ux=cosφsinθcosψ+sinφsinψ，Uy=cosφsinθcosψ-sinφcosψ。

3 反步滑模控制器设计

反步滑模控制结构原理如图1 所示，将飞行系统分成位置和姿态两个子系统，其控制输入是各个位置量当前值与给定值的误差以及姿态量当前值与给定值的误差。

姿态控制器，以滚转通道为例，方程表达式如下：

给定滚转通道期望滚转角为φd=x1d，定义误差变量e1=x1d-x1，对误差变量求导：

引入虚拟控制量α1，定义误差变量：

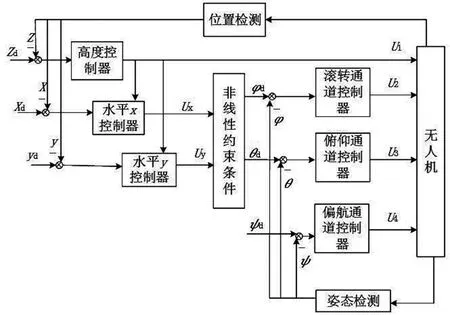
图1 反步滑模控制图

由式（7）（8）可知：

取α1=x˙1d+c1·e1(c1＞0)时：

推出：

式（11）中含有-e1·e2项，系统不稳定，为了消除-e1·e2项，取Lyapunov 函数：

取滑模面：

对式（14）求导得：

将式（7）（13）（15）代入式（16）可得：

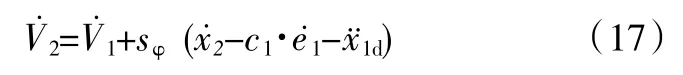
即：

规定指数趋近律为：

将式（18）（19）代入式（6）得：

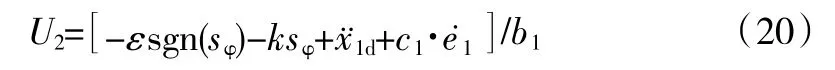
略去高阶分量：

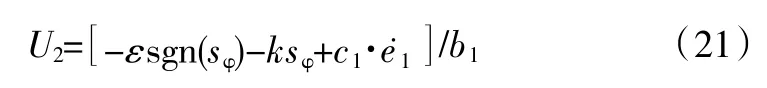
其中e1=x1d-x1，滑模面

给定俯仰控制通道期望俯仰角θd=x3d，同理求得：

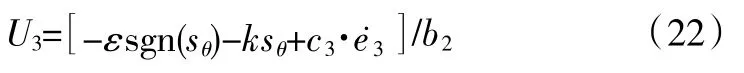
其中e3=x3d-x3，滑模面sθ=e4=-c3·e3，c3＞0。

给定偏航控制通道期望偏航角ψd=x5d，同理求得：

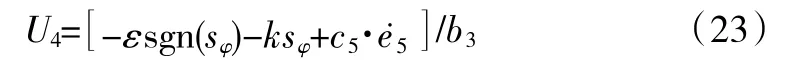
其中e5=x5d-x5，滑模面sφ=e6=--c5·e5，c5＞0。

位置控制器和姿态控制器设计方法一样。对于高度控制器与水平位置控制器，给定高度通道期望高度zd=x7d，U1=其中e7=x7d-x7，滑模面给定水平位置通道x 轴方向期望值，其中e9=x9d-x9，滑模面sx=e10=给定水平位置通道y 轴方向期望值Uy=m其中ey=x11d-x11，滑模面sx=e12=

4 仿真结果

将定点悬停分成垂直起飞、平飞和悬停三个阶段进行控制，飞行任务如下：六旋翼由起飞点，地坐标系下的坐标位置为（0，0，0），垂直起飞到达10 m 高度后，沿X 轴负方向也就是机头方向保持高度不变，飞行10 m 到达目标点（-10，0，10）后悬停。为了验证控制器的鲁棒性，在同等要求下，与采用串级PID 控制器控制的多旋翼进行对比。

给定干扰为无人机质量以函数m=m0－0.2t 形式逐渐减小，其中m0是六旋翼本身质量和负载质量的总和（所加负载质量为5 kg，在20 s 时间内，负载质量不会减到0）。仿真时，规定到给定高度或水平距离的误差范围为（-0.2，0.2）。反步滑模控制器给定各参数为：ε=0.2，c1=c3=c5=1.1，k=1.3，c7=c9=1.2，c11=1.3。

干扰条件下串级PID 及反步滑模控制器对比如图2 所示。从图2 中可以看出，串级PID 控制器控制效果较差，垂直起飞和平飞两个阶段用时比反步滑模控制器控制长，反步滑模控制在2 s 第一次到10 m 高度，开始平飞，串级PID则在8 s。另外虽然反步滑模法高度曲线的超调比串级PID大，但是串级PID 却有两个较大波动，且波动时间长，约为反步滑模法的3 倍。由二者X 轴曲线变化可以看出，反步滑模法控制曲线超调小，变化相对稳定，用时较少，能够较快到达给定位置。

综上，反步滑模控制器相较与串级PID 控制器，在有干扰存在时的控制效果更好，响应时间和速度均优于串PID，抗干扰能力强，能够完成无人机飞行控制任务，且控制效果好。

结合无人机负重飞行实际情况，可能出现载重物突然掉落的情况，选取平飞阶段的某一时刻给定突发干扰，继续对两个控制器的控制效果进行对比，具体为：反步滑模控制器在5 s 时突加一干扰，令质量瞬间减少3 kg 后继续以每秒减少0.2 kg 负载飞行。串级PID 则在9 s 时加入这一干扰。反步滑模控制器参数ε=0.4，c7=1.3，其余参数不变。

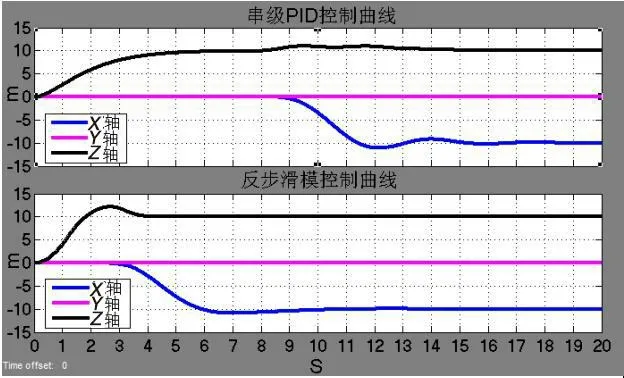
图2 干扰条件下串级PID 及反步滑模控制器对比

由图3 可以看出加入突发干扰之前，各控制器的控制曲线和1 一样没有变化，从加入突发干扰开始，串级PID 控制曲线振荡明显，高度曲线直到最后也没有稳定在10 m 高度，而反步滑模控制曲线和1 没有大致变化，只有X 轴曲线振荡较1 相对明显。

综上，在有突发干扰的情况下，反步滑模控制器仍能保持很好的控制效果，能够应对飞行过程中的突发状况，实现准确定点和稳定悬停，而串级PID 控制器则不能应对突发情况，在干扰较大时，控制精度差。因此，在对控制精度要求较高，外界环境不稳定的情况下，反步滑模控制器比串级PID 控制器有明显优势。

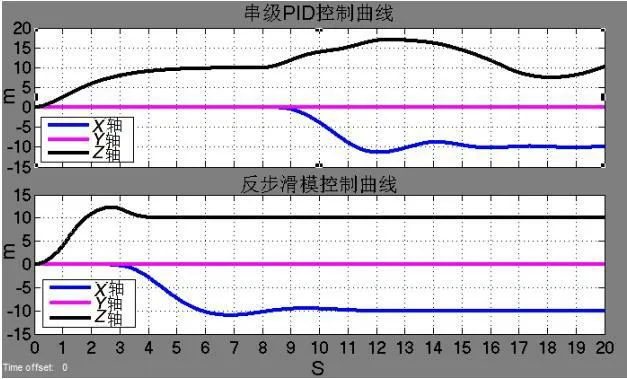
图3 突发干扰下串级PID 和反步滑模法控制曲线对比

5 结束语

针对六旋翼飞行过程中存在干扰的影响，采用反步法与滑模变结构相结合的方法设计控制器，并做了以无人机质量改变为干扰的仿真，通过仿真结果可以看出，反步法与滑模变结构相结合设计的控制器，在干扰条件下对无人机有较好的控制效果，鲁棒性较强。

通过对比仿真实验，更加突显了其优秀的抗干扰能力，从仿真图可以看出，反步滑模控制器响应速度更快，飞行时间更短，鲁棒性强。