随机需求下考虑服务水平的双渠道闭环供应链决策
宁艳荣,宋凤祥
(中铁华铁工程设计集团有限公司,北京 100000)
一、引 言
随着科技的快速发展,一种新的经济发展形势逐渐形成:互联网与传统产业融合,基于“开放、平等、互动”理念的网络平台应运而生,线上购物渠道受到广大消费者的青睐。近年来,网络销售已成为制造业企业创新的侧重点。许多公司,如海尔和华为等,已经建立了销售平台。2019年5月7日,亚马逊网络销售总销售额达到2 135亿元,这刺激了众多厂商开通网上渠道,直接向消费者销售产品[1]。Zhu等[2]认为,制造商开展线上销售业务降低了市场需求对传统线下零售渠道的依赖,线上销售渠道的建立为线下零售商的销售带来了极大的挑战,同时也降低了传统渠道进一步提高售后服务水平的愿望。张雪梅等[3]提出,O2O模式中线下门店的服务增加了线上线下渠道的需求量,实现了利润的增加。Wang等[4]提出,科学技术的发展使产品具有易逝性及生命周期短的特点,多种消费渠道的快速发展导致消费者的消费偏好不断变化,市场中越来越多的因素导致产品市场需求的高度不确定性。需求的随机性严重影响线上线下两个渠道的库存管理,在需求随机时有效控制两个渠道的库存至关重要。
Aviv等[5]认为,随着互联网技术的发展和消费者环保意识的增强,开展双渠道闭环供应链(CLSC)是未来供应链发展的重要方向,对废旧产品进行再制造是发展制造业和保护环境的重大创新。Giri等[6]提出,闭环供应链就是研究产品的回收和再制造的过程,是将正向物流和逆向物流结合在一起的供应链。她认为产品回收有利于环境保护,可促进经济的良性发展。Zhou等[7]认为,闭环供应链包括传统的供应链业务和产品的回收及再制造,闭环供应链加强了各渠道主体和顾客之间的联系。Fleischman等[8]认为,研究闭环供应链的主要目的是响应政府提倡的资源整合政策以获得经济效益。Bhatnagar等[9]认为,需求是不确定的,他们研究了双渠道供应链的库存问题,运用系统动力学的理论与方法构建了双渠道供应链库存独立系统、单级库存合作系统和多级库存合作系统的动力学模型。Modak等[10]提出,需求的不确定性增加了闭环供应链管理的难度,研究市场需求的随机性是降低闭环供应链系统复杂性的重要途径。
近年来,随着电商行业的兴起,消费者消费渠道的多样化使线上线下销售渠道之间的竞争日益激烈,双渠道服务水平的高低严重影响了消费者的渠道选择。Ruiz-Torres等[11]认为,服务水平是指消费者对其所获得的服务要素以及这类要素的构成形态的一种心理预期和期待。Chen等[12]认为,服务水平的内涵是企业为了满足消费者的物流需求,开展一系列活动的结果,物流的本质就是服务,具有优质服务水平的企业在市场竞争中占据优势地位。优质的服务可以提高企业的竞争力,从而吸引更多顾客,提高服务水平是每个企业亟待解决的问题。刘露[13]认为,在O2O模式中,整合双渠道供应链的服务质量有助于提高供应链的整体利润。企业为消费者提供的一系列服务包括产品介绍、送货、安装、调试、维修、技术培训、上门服务等,服务水平为消费者对所享受服务的满意度,满意指数越高代表服务水平越高。
禹海波等[14]研究了由多个供应商组成的供应链系统中供应不确定性因素,建立了多供应商成本分摊机制,提出零售商的最佳订购决策。闻卉等[15]在双渠道环境下,针对不同渠道权力结构对闭环供应链最优决策的影响情况,建立了双渠道定价协调机制。在双渠道供应链中,研究多个主体之间的合作机制有利于促进供应链整体收益的提高。
目前,针对考虑服务水平双渠道闭环供应链的研究较少。在随机需求条件下,本文研究考虑服务水平的双渠道闭环供应链的决策问题。通过建立利润最大化决策模型,解出集中决策和分散决策最优解。为了使供应链良好发展,提出制造商分摊零售商部分服务成本的决策,建立需求随机时双渠道闭环供应链服务成本分摊模型,并解出最优成本分摊系数。通过仿真算例分析,本文验证了制造商分摊部分服务成本策略的可行性和有效性。
二、问题描述与符号说明
(一)问题描述
以需求的随机性为研究背景,以可回收再制造的电子产品(如手机、相机、电视、电脑等)为研究对象,研究考虑服务水平的双渠道闭环供应链决策的问题。该供应链结构如图1所示。

图1 供应链结构示意图
1.双渠道闭环供应链
双渠道闭环供应链由一个制造商和一个零售商组成。制造商既生产新产品,也开展回收再制造,新产品和再制造产品在本质上没有差别,销售价格相同。制造商开展线上销售渠道,零售商通过线下渠道售卖产品,零售商为两个渠道的消费者提供售后服务。
2.考虑服务水平的双渠道闭环供应链
系统的运作过程如下:
(1) 制造商以单位生产成本c生产新产品,制造商将部分生产的产品以w的批发价格卖给线下渠道的零售商,零售商再以p2(c (2) 零售商为两个渠道的消费者提供售后服务,服务水平为S。制造商从消费者手中以单位回收价格bR回收产品,将回收的废旧产品以单位再制造成本cR进行再制造,再制造后的产品同新制造产品在本质上没有区别,可以一起销售,销售过程与过程(1)相同。 假设1:再制造产品和新产品的销售价格一致(考虑一个技术相对完善的市场); 假设2:线上渠道和线下零售渠道产品的销售价格不同(制造商和零售商以各自利益最大化为目标,因此产品定价不同); 假设3:回收后的产品可以全部进入再制造流程(无法再制造的产品直接进入废品处理流程); 假设4:零售商为两个渠道的全部产品提供售后服务,开展线上渠道的制造商不提供此类服务; 假设5:允许缺货和库存积压(需求的不确定可造成缺货和库存积压现象的出现); 假设6:在双渠道供应链中,两个渠道的需求不确定性情况不同,假设两个渠道的需求不确定性是相互独立的。 1.双渠道供应链市场可预测部分需求 d1=φa-b1p1+bp2+(1-σ)λS d2=(1-φ)a-b2p2+bp1+σλS 其中,a为潜在市场总需求;φ为线上渠道初始需求所占潜在市场总需求比例,且0≤φ≤1;λ为消费者对零售渠道提供服务的敏感系数;S为传统渠道提供的服务水平(制造商线上直销配送的产品售后服务为0,零售商为线上订单提供备货服务并为两个渠道售卖的全部产品提供售后服务);c为新产品的单位生产成本,cR为回收产品的单位再制造成本,cR 2. 总服务成本 其中,cs为零售商进行售后服务时的服务成本,η为零售商提供的服务成本系数。 3. 随机需求函数 D1=φa-b1p1+bp2+(1-σ)λS+ε1 (1) D2=(1-φ)a-b2p2+bp1+σλS+ε2 (2) 其中,ε1和ε2是定义在区间[A1,B1]和[A2,B2]的随机变量,均值分别为u1和u2,A和B为闭区间的上下界,0≤Ai≤Bi,Bi⊆∞(i=1,2),标准差为σ1和σ2;累积分布函数分别为F1(x)和F2(x),0≤Fi(x)≤1,i=1,2。 概率密度函数分别为f1(x)和f2(x)。由于需求不确定,制造商和零售商面临缺货损失和库存积压的问题,制造商为线上渠道随机需求准备的部分库存为z1,零售商为线下渠道随机需求准备的部分库存为z2,其中,qi(i=1,2)表示备货库存量,q1为制造商线上销售渠道备货库存量,q2为零售商线下销售渠道备货量。q1=d1+z1,q2=d2+z2,D1为制造商线上销售渠道随机需求量,D2为传统零售渠道的随机需求量。 两个渠道的期末库存积压量为 其中,0≤Λ1≤∞,0≤Λ2≤∞。两个渠道的期末期望缺货量为 (3) 其中,Di(i=1,2)表示市场需求量。期望库存量为 集中决策时供应链总利润为 (4) 其中,γ表示回收率,代表制造商无偿回收(回收价格为0)时回收产品占市场销售产品的比例,0≤γ≤1。将D1、D2、q1、q2、d1,d2、Λ1、Λ2、Θ1、Θ2代入式(4)可得 (5) 集中决策下利润函数关于S、bR、z1、z2的海瑟矩阵为: 其中,海瑟矩阵的一阶顺序主子式为|H1|=-[p1+h1+τ1+γ(c-cR-bR)]f1(z1)<0。该目标函数海瑟矩阵的二阶顺序主子式为|H2|=[p1+h1+τ1+γ(c-cR-bR)]f1(z1)[p2+h2+τ2+γ(c-cR-bR)]f2(z2)>0,可知集中决策时的利润函数是关于随机需求部分最优库存z1和z2的联合凹函数。可得该目标函数海瑟矩阵的三阶顺序主子式为|H3|=[p1+h1+τ1+γ(c-cR-bR)]f1(z1)[γ2(1-F2(z2))2-β(p2+h2+τ2+γ(c-cR-bR))f2(z2)]+[p2+h2+τ2+γ(c-cR-bR)]f2(z2)[γ2(1-F1(z1))2-β(p1+h1+τ1+γ(c-cR-bR))f1(z1)]。因为[p1+h1+τ1+γ(c-cR-bR)]f1(z1)>0,[p2+h2+τ2+γ(c-cR-bR)]f2(z2)>0,同时0<γ<1,那么0<γ2<1。[p1+h1+τ1+γ(c-cR-bR)]f1(z1)和[p2+h2+τ2+γ(c-cR-bR)]f2(z2)为各自渠道的销售价格、库存持有成本、缺货损失成本、单位节约成本与回收率乘积4部分之和同需求随机部分的概率密度函数的乘积。其中,销售价格、库存持有成本、缺货损失成本三部分之和远大于1,现实可取。同样,在回收过程中,消费者对回收时的价格关注度要高于回收价格为0时的关注度,那么无偿回收的回收率越低,表示消费者对有偿回收的回收价格越敏感,0≤γ<β<1可取。随机需求部分的概率密度函数在本文中可以无限大,其只需满足累积分布函数0≤1-Fi(zi)≤1,可以得出γ2(1-F1(z1))2-β(p1+h1+τ1)f1(z1)<0,γ2(1-F2(z2))2-β(p2+h2+τ2)f2(z2)<0,由此可得出三阶顺序主子式为|H3|<0。该目标函数海瑟矩阵的四阶顺序主子式为|H4|=[p2+h2+τ2+γ(c-cR-bR)]f2(z2)η[2β[p1+h1+τ1+γ(c-cR-bR)]f1(z1)-γ2(1-F1(z1))2]。四阶顺序主子式同该目标函数的三阶顺序主子式验证过程相同,由此可以得出2β[p1+h1+τ1+γ(c-cR-bR)]f1(z1)-γ2(1-F1(z1))2>0,|H4|>0。因此,利润函数是关于z1、z2、bR、S的严格凹函数。 求利润函数关于z1、z2、bR、S的一阶导数,并令其等于0可得 (6) (7) (8) (9) 将式(8)带入式(9)可得 命题1:集中决策下,供应链总利润随零售商提供的售后服务成本系数的提高而下降。 在分散决策时,制造商和零售商是相互独立的,他们试图最大限度地提高自己的预期利润,而不考虑供应链总体的预期利润。制造商和零售商各自以自身利益最大化为最终目标,斯坦博格两阶段动态博弈模型如下 ΠM=p1[Emin(D1,q1)]+w(d2+z2)-c(d1+d2+z1+z2)+(c-cR-bR)[γ(Emin(D1,q1)+Emin(D2,q2))+βbR]-h1Λ1-τ1Θ1 (10) (11) 该模型采用反向归纳法求解。考虑第二阶段的博弈,零售商选择服务水平使自身利润最大化,将需求函数代入式(10)可得 (12) 根据零售商的利润函数,海瑟矩阵为 求零售商利润函数关于S、z2的一阶导数并令其等于0,可得 (13) (14) 接下来,考虑第一阶段博弈,将所得服务水平式(13)代入制造商的利润函数式(10),可得 ΠM=p1[Emin(D1,q1)]+w(d2+z2)-c(d1+d2+z1+z2)-h1Λ1-τ1Θ1+ 求利润函数关于w、bR、z1的一阶导数并令其等于0,可得 (15) (16) (17) 将式(15)带入式(16)可得 命题2:分散决策下,当(p1-c)(1-σ)λ+(w-c)σλ+γ(c-cR-bR)λ>0时,零售商提供的服务水平越高,制造商获得的利润越高。 其中,S*为分散决策时零售商为顾客提供的售后服务水平。 零售商为双渠道销售的产品提供售后服务,双渠道的需求随之增加,零售商的服务成本也随之增加。为了使双方更好地合作,需要制造商分摊零售商的部分服务成本。假设零售商分摊φ(0≤φ≤1)倍的服务成本,制造商分摊剩余1-φ倍的服务成本。此时,制造商和零售商的利润函数为 (18) (19) 同分散决策的求解过程相似,该模型采用反向归纳法求解。考虑第二阶段的博弈,零售商选择提供服务水平使自身利润最大化,将需求函数代入式(19)可得 (20) 根据零售商的利润函数可得海瑟矩阵为 求零售商利润函数关于S、z2的一阶导数并令其等于0,可得 (21) (22) 考虑第一阶段博弈,将所得服务水平式(21)代入制造商的利润函数式(18)里,可得 求利润函数关于w、bR、z1的一阶导数并令其等于0,可得 (23) (24) (25) 将式(23)代入式(24)可得 分摊成本后,为了更好地对此各决策变量、利润与集中决策和分散决策模型,在服务成本分摊决策的双渠道闭环供应链中,假设随机需求ε1和ε2服从[0,10]上的均匀分布,那么各决策变量为 其中,D、H、K为所给公式的缩写,HD代表公式H和公式D的乘积,KD代表公式K和公式D的乘积。 将所得决策变量代入制造商的利润函数,并对制造商的利润函数求关于成本分摊系数的导数,令其等于0,可得 本文利用Matlab软件进行仿真分析。假设参数a=30,φ=0.51,λ=0.5,c=9,cR=2,p1=20,p2=25,b1=0.57,b2=0.4,b=0.2,σ=0.7,γ=0.1,β=0.8,η=0.5,τ1=3,τ2=2,h1=2,h2=3;同样随机需求部分ε1和ε2服从[0,10],那么0≤z1≤1,0≤z2≤1。计算结果如表1所示。 表1 分散决策、集中决策与服务成本分摊后最优决策结果 数值分析的仿真结果如图2所示。 图2 分散决策下服务水平对供应链利润的影响 图2表明,在分散决策下,随着零售商服务水平的提高,制造商和零售商的利润也不断提高,说明零售商应提高服务水平促进利润的提高,制造商应该鼓励零售商提高服务水平。 图3显示,制造商无偿回收的回收率对回收价格的影响。回收率提高时,回收价格随之下降,说明废旧产品回收率的高低和回收价格关系不大。因此,制造商可降低回收价格来减少废旧产品回收成本支出。如图3所示。 图3 回收率对回收价格的影响 在分散决策下,零售商的服务水平随批发价格的下降而提高。为了响应制造商批发价降低策略,零售商会提高服务水平,从而促进供应链总体利润提高。如图4所示。 图4 分散决策时批发价格对服务水平的影响 服务成本分摊决策可以使供应链总体利润高于集中决策、分散决策时供应链的总体利润。因此,制造商进行部分服务成本分摊的决策优于集中决策和分散决策。如图5所示。 图5 服务水平对供应链总利润的影响 本文提出如下建议: (1) 当废旧产品无偿回收的回收率高于有偿回收的回收率时,制造商应该通过降低废旧产品的回收价格来节约回收再制造成本,从而提高供应链总体利润。 (2) 当零售商的服务成本过高,制造商的利润会随着零售商为消费者提供的售后服务水平的提高而增加。为了使零售商提供较高的服务水平,制造商有必要通过降低产品批发价格来鼓励零售商售后服务水平的提高。 (3) 需求不确定时,在分散决策下,需求随机且服从某区间上的均匀分布时制造商可以采取降低产品批发价格策略促进零售商服务水平的提高。同时,制造商可回收更多的废旧产品进行产品再制造来节约单位产品的制造成本。零售商应该尽量降低单位持有成本,为线下销售渠道随机需求部分准备更多的库存来促进利润的增加。 (4) 无论是集中决策还是分散决策,零售商为消费者提供售后服务都会产生服务成本,零售商服务水平越高,制造商的利润随之提高。为了使双方更好的合作制造商分摊零售商部分服务成本可以使零售商服务达到最优水平,双方利润达到最大化。(二)假设条件
(三)参数定义




三、决策模型
(一) 集中决策模型


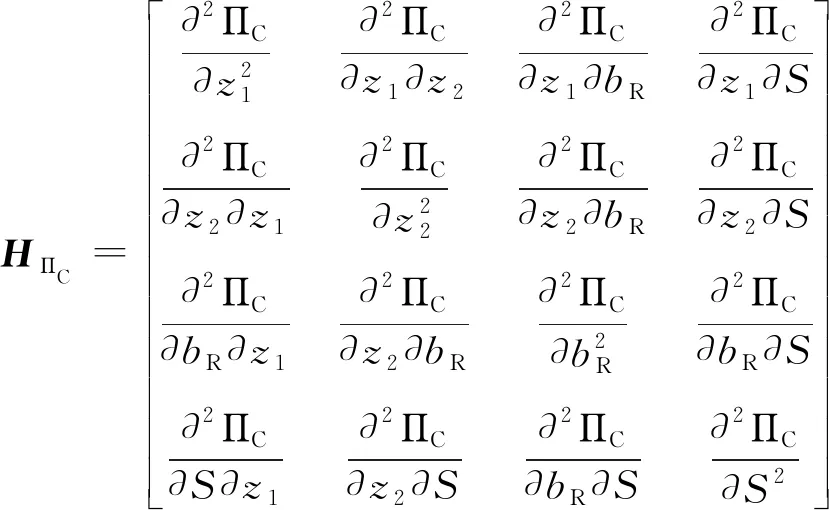
(二)分散决策模型

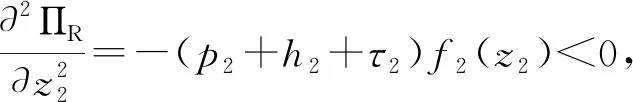
(c-cR-bR)[γ(Emin(D1,q1)+Emin(D2,q2))+βbR]


(三)制造商服务成本分摊决策模型
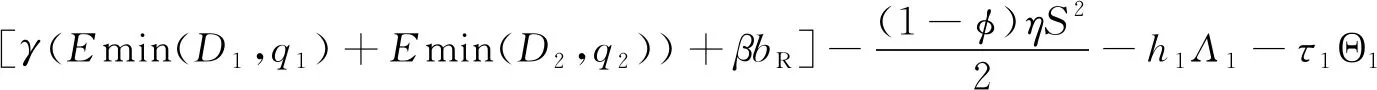
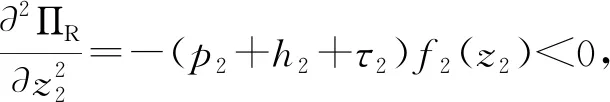
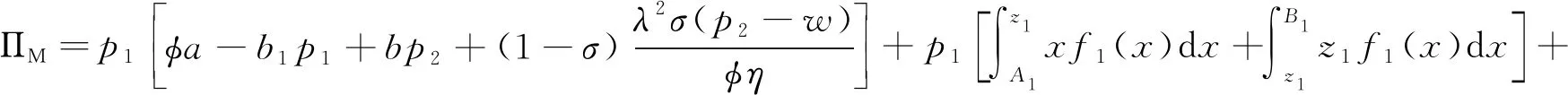
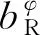

四、算例分析





五、结束语

