Enhancements of the Gaussian network model in describing nucleotide residue fluctuations for RNA
Wen-Jing Wang(王文静) and Ji-Guo Su(苏计国)
Key Laboratory for Microstructural Material Physics of Hebei Province,School of Science,Yanshan University,Qinhuangdao 066004,China
Keywords: Gaussian network model(GNM),B-factor,RNA molecules
1. Introduction
RNA is one of the important biological macromolecules in the cell. For a long time, RNA is considered to be only served as a messenger that intermediates the transmission of the genetic information from DNA to protein sequence.[1]However, in recent decades more and more evidences have revealed that the biological functions carried out by RNA are much broader than we previously believed. It is increasingly realized that RNA can perform various functions including catalysis of biochemical reactions, regulation of biological processes, transduction of cellular signals, synthesis of proteins,post-translational modification of proteins,regulation of gene expressions, and so on.[1–4]Similar to proteins, RNA can fold into subtle tertiary structures,and the biological functions of RNA are essentially determined by its specific threedimensional structure and the intrinsic dynamics encoded into the structure.[3–9]How to effectively extract the dynamical properties from the tertiary structure of RNA is critical for our understanding of RNA functions.
Elastic network model (ENM) describes a biomacromolecule as a group of nodes connected by springs,which is a simple and efficient method to investigate the intrinsic dynamics of biological macromolecules based on their native structures. ENM has been extensively used to analyze the conformational dynamics of proteins.[10–14]Many studies have proved that the residue fluctuations in proteins calculated by ENM are well consistent with the B-factors measured by x-ray crystallographic experiments as well as the results obtained by molecular dynamics (MD) simulations.[15]In addition,ENM has also been successfully applied in investigating the function-related collective motions, predicting folding cores and functional hotspots, identifying allosteric signaling pathways,enhancing conformational sampling in MD simulations,and realizing protein–protein soft docking.[16–21]In recently years,ENM has been extended to study the structure-encoded dynamic properties for RNA.Yang et al.constructed ENM for DNA/RNA-containing systems and the computed nucleotide fluctuations by ENM exhibit a quite good positive correlation with the experimental B factors.[22]Pinamonti et al. systematically assessed the performance of ENM by using different types of RNA structures,and they found that this simple model can properly reproduce the structural fluctuations obtained by all-atomistic MD simulations and SHAPE experiments.[23]The study of Zimmermann and Jernigan showed that the low frequency normal modes computed by ENM are capable of capturing the principal components of the structural flexibility determined by NMR experiments for dense-packed RNA molecules.[24]ENM was also utilized by Wang et al. to study the functional cooperative motions for large RNA-containing systems, and the results showed that ENM can provide valuable insights into RNA functional dynamics.[25]The study of Afonin et al. indicated that ENM can characterize the experimentally observed dynamic behaviors of large RNA cubic nanoscaffolds.[26]
Although the usefulness of ENM in characterizing RNA dynamics has been validated, some studies also pointed out that the correlation between the ENM-computed and experimental residue fluctuations is lower for RNAs than that of proteins.[27]It is believed that the lower fluctuation correlation for RNA should be attributed to its loosely-packed tertiary structure compared with the well-packed protein structure.[27–29]In the conventional ENM,the interactions between residues are simplified as springs with a uniform force constant,and the existence of springs between residues is determined by their pairwise distance less than a given cutoff value.[15,18,22,29,30]Several improved strategies in constructing ENM have been proposed to enhance the performance of the model for RNA. For the nucleotide representation in ENM, the research work of Pinamonti et al. showed that the all-atomistic and three-nodes-per-nucleotide models are better than the single-node-per-nucleotide model in investigating RNA structural dynamics.[23]Diggins et al. further explored that the coarse-grained site selection in nucleotide representation also influences the performance of the ENM.[31]For the inter-nucleotide interactions in ENM, Mailhot et al. adopted a sequence-dependent potential function,which takes into account the chemical properties of the residues,to construct the elastic network contact model(ENCoM).It is found that ENCoM can better simulate the dynamics of RNA compared with the conventional ENM.[32]Moreover,the study of Wang et al.illustrated that a multiscale ENM,in which the multiscale harmonic interactions with variable force constants were adopted,distinctly improves the characterization of the dynamical properties of RNA. However, in the multiscale ENM, the force constants need to be optimized by using the experimental Bfactors for each studied RNA molecule separately, and thus the optimized model for one RNA molecule is not generally applicable for other RNA systems.[33]
In the present work,two novel approaches are proposed to improve the performance of the ENM in describing the structural flexibility of RNA molecules. As mentioned above, in the conventional ENM the interaction strength is assumed to be identical for all the nucleotide pairs. In this study,the difference in the inter-nucleotide interaction strength is taken into account to build a weighted ENM(wENM),in which the force constant for each spring is weighted by the number of interacting heavy atom pairs between the two related nucleotides.Besides that, another simplification in the conventional ENM is that the inter-nucleotide interactions are neglected for the nucleotide pairs beyond a given cutoff distance. However,the nucleotides in RNA molecules are negatively charged,and the long-range electrostatic interactions are important for RNA structural dynamics. The construction of ENM based on a cutoff distance in the conventional method for proteins may be not suitable for RNA molecules. Aimed at this problem,another new ENM-building method, named force-constantdecayed ENM (fcdENM), is proposed. In our method, the distance cutoff is removed and all residue pairs are connected by springs with the force constant decayed exponentially with the separate distance. The performance of these two proposed models(wENM and fcdENM)is tested by using a large nonredundant RNA structure dataset.Our calculation results show that both the proposed models outperform the conventional ENM in prediction of the experimental B-factors.
2. Materials and methods
2.1. The conventional Gaussian network model
Gaussian network model(GNM)is one type of the ENM,which is built based on the coordinates of RNA structures downloaded from the Protein Data Bank(PDB).In GNM,each nucleotide in RNA structure is treated as a node located on its P atom. The inter-nucleotide interactions are represented by a linear harmonic potential, where each node in the model is connected by springs to other nodes within a given cutoff distance and the force constant for all the springs is identical.[34]The potential function of the GNM for a RNA molecule is the sum of the harmonic potential energies of all the springs in the model,which can be written as

here Rcis the cutoff distance, which is used to determine whether or not there exist inter-node springs.
According to the normal mode analysis theory, the dynamical properties of the RNA system are fully determined by the Kirchhoff matrix Γ. The normal modes of the system can be calculated through diagonalization of the matrix Γ, and the details of the calculation can be found in the references.[15,18,22,29,30,34]Based on the statistical thermodynamic theory,the mean-square fluctuation for each nucleotide can be computed as

whereV is the potential function of the system given in Eq.(1);kBis the Boltzmann constant;T is the temperature;ukand λkare the ktheigenvector as well as the corresponding eigenvalue of Γ, which represent the kthnormal mode and the square of the frequency of the mode,respectively.Then,the B-factor for each nucleotide can be obtained by using the Debye–Waller formula
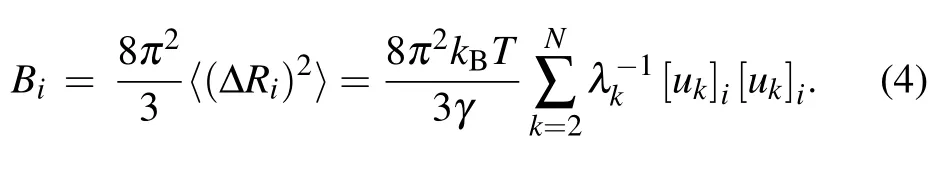
In the present work, the theoretical B-factors calculated by Eq. (4) are compared with the experimental data obtained by x-ray crystallographic method to assess the performance of the conventional GNM as well as our proposed new models. The Pearson correlation coefficient (PCC) is used to evaluate the accuracy of the predicted B-factors relative to the experimental data. The PPC between the predicted and experimental Bfactors can be expressed as

2.2. Weighted Gaussian network model
In the conventional GNM, the same force constant is adopted for all the springs in the model. However,RNA structure and dynamics are controlled by various inter-nucleotide interactions, in which the covalent interactions as well as the base–base paring and stacking are much stronger than other interactions.[35–38]The various interactions with different intensities play different roles in controlling RNA structural stability and dynamics.[35–38]For better characterizing RNA structural dynamics,the variation of interaction strength should be considered. In the present work, a weighted GNM(wGNM)was proposed,in which the differences in the strength of the inter-nucleotide interactions was taken into account by using different weights. In our model,the force constant for each spring was weighted simply by the number of atom–atom contacts between the corresponding pairwise nucleotides.
The proposed wGNM was built according to the following procedure.
(1)Based on the coordinates of all the heavy atoms in the RNA structure, the atom–atom contacts were determined by a given atomistic cutoff distance. An atom was considered to form a contact with another atom if their distance is less than the cutoff value. Otherwise,no contact exists between them.
(2)Similar to the conventional GNM,each nucleotide in the RNA structure was simplified as a node located on its P atom to construct the nucleotide-level coarse-grained model.But different from the conventional GNM, whether or not a spring exists between pairwise nucleotides was determined by the atomistic contacts between them,instead of the nucleotidelevel distance cutoff. If a heavy atom in a nucleotide forms contact with any heavy atom of another nucleotide,these two nucleotides were considered to be interacted with each other and they were connected by a spring. Besides that,in wGNM,the force constant specific to each spring was weighted by the total number of atom-atom contacts between the corresponding nucleotides.
(3) Based on the above model-construction method, the Kirchhoff matrix Γ for wGNM can be computed as

where nijis the total number of heavy atom contacts between the ithand jthnucleotides. Then,the normal modes of the system can be calculated through diagonalizing the matrix Γ,and the nucleotide B-factors of the RNA structure can be computed by using Eqs.(3)and(4).In this study,the computed B-factors were compared with the experimental data by using the PCC calculated with Eq.(5)to evaluate the accuracy of wGNM.
2.3. Force-constant-decayed Gaussian network model
As noted in our previous discussion, a distance cutoff was used to determine whether an interaction exists between two nucleotides,and the force constant for all the internucleotide interactions was assumed to be identical in the conventional GNM.However,the nucleotides in RNAs are negatively charged, and the conventional cutoff-based GNM construction method may lead to the neglect of the long-range electrostatic interactions that are weak but important for RNA structural dynamics. In the present study, another new GNM construction method was proposed,in which the distance cutoff was removed and all the pairwise nucleotides were connected by springs with the force constant decayed exponentially with their separate distance.
In our proposed force-constant-decayed GNM(fcdGNM),the Kirchhoff matrix Γ can be calculated as

2.4. Dataset of the non-redundant RNA tertiary structures
In this study,the proposed new models,i.e.,wGNM and fcdGNM, were tested by using a non-redundant RNA structure dataset, and the calculation results were compared with those computed by the conventional GNM to evaluate the performance of these models. The non-redundant RNA tertiary structures were obtained from the representative sets of RNA 3D structures collected by Leontis and Zirbel.[39]The accuracy of the experimental B-factors largely depends on the resolution of RNA structures determined by x-ray crystallography.Higher resolution generally implies more precise of B-factor values. Therefore,the RNA crystal structures with 3.0 ˚A resolution or better were chosen in our study.In addition,the GNM is more applicable to the well-packed micromolecular structures.However,the RNA structures with small size are usually loosely-packed and also generally complexed with proteins or other RNAs. The binding partners may have significant influences on the dynamics of the small-size RNA.Thus,in the present work, only the large-size RNA structures were considered. Based on the above considerations,the following filter criteria were used to get the RNA structure dataset for our studies from the representative set 3.128 of RNA 3D structures released on May 27 in 2020:(1)structural determination by xray crystallographic experiments;(2)structural resolution better than 3.0 ˚A;(3)the number of nucleotides in RNA structure larger than 122; (4) the nucleotide B-factor data having been measured. According to the above criteria,a total of 51 RNA structures were obtained as the database for the present work.The PDB codes of these RNA structures are listed in Table S1 in the supplementary materials.
3. Results and discussion
3.1. The optimization of the variable parameters in the models
In the conventional GNM, the cutoff distance Rcis the only adjustable parameter. In order to investigate the effect of the cutoff value on the calculation results, the PCC between the predicted and experimental B-factors was computed for different discrete values of Rc. Figure 1(a) shows the change of the average PCC for all the RNA structures in the nonredundant dataset with the value of Rcincreasing from 9 ˚A to 23 ˚A with an interval of 1 ˚A. The PCC values with different cutoff distances for each individual RNA molecule in the dataset are given in Table S2 in the supplementary materials.It is found that the cutoff value has obvious influence on the computation results,where the average PCC between the predicted and experimental B-factors is in the range of 0.463–0.518.The maximum average PCC value is 0.518, which corresponds to the cutoff distance of 12 ˚A.In the present study,the cutoff of 12 ˚A was used in our calculation for the conventional GNM.

Fig.1. The change of the average PCC between the predicted and experimental B-factors for the RNA structures in the non-redundant dataset calculated with different discrete values of the variable parameters in the models. (a) The change of the average PCC computed by the conventional GNM with different values of the cutoff distance Rc. (b)The change of the average PCC calculated by the wGNM with different values of the atomistic distance cutoff. (c)The change of the average PCC with the variation of the σ value computed by the fcdGNM.
For the proposed wGNM, the only variable parameter is the atomistic distance cutoff, which is used to determine the formation of contacts between heavy atoms. To explore the impact of the atomistic cutoff value on the performance of wGNM, the PCC between the predicted and experimental Bfactors was calculated with twelve discrete cutoff values of 3.8 ˚A,4.0 ˚A,4.2 ˚A,4.4 ˚A,4.6 ˚A,4.8 ˚A,5.0 ˚A,5.2 ˚A,5.4 ˚A,5.6 ˚A,5.8 ˚A,6.0 ˚A,respectively. The calculation results are shown in Fig. 1(b) and Table S3 in the supplementary materials. From Fig. 1(b), it is found that the average PCC of the RNAs in the database was varied from 0.553 to 0.569 when the above different cutoff values were adopted. For the cutoff value of 4.2 ˚A,the average PCC reached the highest value of 0.569. Thus,in this study,4.2 ˚A was adopted as the atomistic distance cutoff value for the wGNM.
In the proposed fcdGNM,σ is the only adjustable parameter as discussed in Eq. (7). The influence of the σ value on the calculation results was studied, in which the value of σ increased from 5 ˚A to 16 ˚A with a step of 1 ˚A and the PCCs between the predicted and experimental B-factors were calculated for each σ value. Figure 1(c)displays the change of the average PCC with the variation of the σ value. The detailed PCC values for each RNA molecule in the non-redundant database can be found in Table S4 in the supplementary materials. From Fig.1(c),the maximum value of the average PCC is 0.553 with the parameter σ to be 16 ˚A. Therefore, the parameter σ was set to be 16 ˚A for the fcdGNM.
3.2. The improved performance in reproduction of the experimental B-factors by our proposed models
For each RNA in the non-redundant database, the conventional GNM as well as the proposed wGNM and fcdGNM were respectively constructed based on the RNA crystal structure. The nucleotide B-factors were calculated by these three models,respectively,where the optimal value of the adjustable parameters in the models was used in the calculations as discussed in the previous section. Then, the PCCs between the predicted and the experimental B-factors were computed for wGNM, fcdGNM, and the conventional GNM, respectively,to evaluate their performance in reproducing the experimentalobserved RNA structural dynamics. The PCC values obtained by the three models for all the 51 RNA structures in the nonredundant database are given in Table 1. The results show that the average PCC value is increased from 0.518 to 0.569 for the wGNM compared with the conventional GNM.The proposed new model,i.e.,wGNM,obviously raises the B-factor prediction accuracy by 9.85%. For the other new model fcdGNM,the average value of PCCs is also improved from 0.518 to 0.553,with the increase rate of 6.76%. These results indicate that both our proposed models exhibit better performance in prediction nucleotide fluctuations than the conventional GNM.Our non-redundant dataset contains different types of RNA including ribosome,ribozyme,riboswitch,and other types. The performance of our proposed methods for different types of RNA was also evaluated separately. For ribosomal RNAs,the average PCC is improved from 0.579 to 0.657 and 0.645 for wGNM and fcdGNM, respectively. For ribozyme RNAs, the average PCC is increased from 0.507 to 0.547 and 0.524 for wGNM and fcdGNM,respectively. For riboswitch RNAs,the value is improved from 0.382 to 0.562 and 0.503 for wGNM and fcdGNM,respectively.These results indicate that our proposed methods outperform the conventional GNM for all these different RNA types.
From Table 1,it is found that the nucleotide B-factors of 8 RNA systems cannot be calculated by the conventional GNM due to more than one mode with zero frequency. The reason is that these RNA structures are not well packed and the number of springs connected to some nucleotides in these systems is too little. Several studies have also pointed out that the GNM is more applicable for tightly packed structures rather than the loosely packed structures.[40]Our fcdGNM method can effectively overcome this defect in the conventional GNM, where all the pairwise nucleotides were connected by springs in the fcdGNM and the force constant decayed exponentially with the pairwise separate distance. The results in Table 1 exhibit that the B-factors for these 8 RNA molecules can be effectively predicted by using our fcdGNM method. It should also be noted that the PPC values predicted by the conventional GNM for two RNA systems,i.e.,chian B of 5T2A and chain E of 5T5H,are negative.The crystal structure of these two systems was checked manually,and it is found that the calculated RNA chain is packed tightly with other surrounding chains. In our calculation, only the studied RNA chain was considered separately,and the impacts of the surrounding chains were not taken into account,which may be responsible for the negative value of PCC.For the remaining 41 RNA structures,the PCC values predicted by the conventional GNM are positive and the average PCC is 0.557.
The 41 RNA structures with positive PCC values in the conventional GNM were also calculated with the new proposed wGNM and fcdGNM, as listed in Table 1. The average PCC is 0.631and 0.612 for wGNM and fcdGNM,respectively. Compared with the conventional GNM, the average PCC improved respectively by 13.3% and 9.87% for wGNM and fcdGNM, which indicates that the proposed models can obviously enhance the performance of GNM in describing RNA structural dynamics. From Table 1,it is also found that most of the RNAs with negative PCC values in the conventional GNM also exhibit negative PCC values in the wGNM and fcdGNM. This result implies that our proposed models have little effect on the RNA systems that are not suitable for the application of GNM.

Table 1. The PCC values for all the 51 RNA structures in the non-redundant database obtained by the conventional GNM,wGNM,and fcdGNM,respectively.
It should be noted that the most time and memory consuming operation in the calculation of GNM is the diagonalization of the Kirchhoff matrix. For the proposed wGNM,the atomistic information was implicitly taken into account, and the size of the Kirchhoff matrix in wGNM is the same as that of the conventional GNM. For the fcdGNM, each nucleotide in the RNA structure is simplified as a node and the dimension of the Kirchhoff matrix is also same as that of the conventional GNM. Therefore, compared with the conventional GNM,these two new models have improved performance but do not increase the calculation burden.
3.3. Case study
In order to illustrate the improved performance of wGNM and fcdGNM relative to the conventional GNM in extracting the nucleotide fluctuations in RNA structures, the “AA”chain of the chloroplast ribosome (PDB code:6ERI) was investigated as a case study.[41]The nucleotide B-factors of the studied RNA structure were theoretically predicted by using the conventional GNM as well as the proposed wGNM and fcdGNM, respectively, and the predicted results were compared with the experimental data. The “AA” chain of the chloroplast ribosome is a large-size RNA structure composed of 2696 nucleotides,which forms a well-packed tertiary structure, as shown in Fig. 2(a). The PCC between the predicted and experimental B-factors calculated by the conventional GNM is 0.588. For the wGNM and fcdGNM,the PCC value is obviously improved to 0.841 and 0.744,respectively. These two new models are superior to the conventional GNM.
The exact calculation results of the B-factors by the wGNM and fcdGNM were compared with those by the conventional GNM in Figs.2(b)and 2(c),respectively. It is found that the flexibility of a subdomain composed of 1079–1137 nucleotides, highlighted in red in Fig. 2(a), predicted by the conventional GNM is much lower than the experimental results. This may be caused by the large value of the distance cutoff adopting in the model. The large cutoff value may introduce non-existing interactions between this subdomain with the remain part of the RNA structure,which reduces the fluctuation of the subdomain. While for most of other flexible nucleotides, which correspond to the peaks in the B-factor curves, the fluctuations predicted by the conventional GNM are obviously higher than the experimental observations, as shown in Figs. 2(b) and 2(c). These flexible nucleotides are usually loops and protrude out from the RNA structure. This result indicates that the distance cutoff in the conventional GNM is insufficient to restrict the dynamics of these flexible nucleotides. However, for wGNM, the predicted results are significantly improved. The flexibility of the 1079–1137 subdomain calculated by wGNM agrees well with the experimental data, which is higher than the flexibility predicted by the conventional GNM, as shown in Fig. 2(b). In addition,for other flexible nucleotides corresponding to B-factor profile peaks,the fluctuations predicted by wGNM are also more consistent with the experimental results,which are usually lower than the fluctuations predicted by the conventional GNM, as displayed in Fig. 2(b). These results imply that the wGNM can better capture the interaction distributions in RNA structures than the conventional GNM.For fcdGNM,the predicted results are also better than the conventional GNM.The fluctuations of the flexible nucleotides in protruding loops predicted by fcdGNM are lower than those calculated by the conventional GNM, and they better agree with the experimental results, as shown in Fig. 2(c). But for the 1079–1137 subdomain, the fluctuations predicted by fcdGNM are similar with those predicted by the conventional GNM.
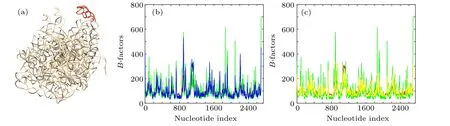
Fig.2. The calculation results for the“AA”chain of the chloroplast ribosome(PDB code:6ERI).(a)The tertiary structure of the“AA”chain of the chloroplast ribosome, where the subdomain composed of 1079–1137 nucleotides is highlighted in red. (b) The nucleotide B-factors predicted by the wGNM(blue color)compared with the results obtained by the conventional GNM(green color)as well as the experimental data(red color). (c)The nucleotide B-factors predicted by the fcdGNM(yellow color)compared with the results obtained by the conventional GNM(green color)as well as the experimental data(red color).
4. Conclusion
More and more evidences have revealed that RNA molecules can fold into subtle three-dimensional structures as proteins and carry out various important functions in many biological processes. The exertion of the biological functions of RNAs depends on their structure-encoded conformational dynamics. How to effectively predict the dynamical properties from the tertiary structure of RNA molecules is important for the understanding of the molecular mechanism of RNA functions. The Gaussian network model (GNM), as one type of the elastic network model(ENM),is an efficient method to explore the intrinsic dynamics of biomacromolecules,which has been widely applied for proteins. In recent years, GNM has also been extended to study the structural dynamics of RNA.However,owing to the more loosely packed tertiary structure,the performance of the conventional GNM on RNAs is not as good as that on proteins. It is a valuable problem worth studying to improve the performance of GNM applied to RNAs.
In the conventional GNM, a cutoff distance was used to construct the model and a uniform force constant was applied for all the nucleotide pairs. Considering the structural characteristics and the various forces distribution properties specific to RNAs, the above simplifications in the conventional GNM may not work well for RNAs. In the present work,aiming at these simplifications, two approaches, i.e., wGNM and fcdGNM, were proposed to improve the application of GNM in investigating the structural dynamics of RNAs. In wGNM, the force constant is specific to the corresponding pairwise nucleotides, which is weighted by the number of atom–atom contacts between them.In fcdGNM,the force constant decays exponentially with the separate distance between the pairwise nucleotides. These two new models were tested by using a non-redundant RNA structure dataset composed of 51 RNAs, and the calculation results show that the proposed two models can better reproducing the experimental B-factors than the conventional GNM.Compared with the conventional GNM,the average PCC between the predicted and experimental B-factors improved by 9.85% and 6.76% for wGNM and fcdGNM,respectively. It is also found that GNM is more applicable for the RNA structures with large size,and 41 out of 51 RNA structures exhibit positive PCC values. For these 41 RNAs, the average PCC computed by wGNM and fcdGNM is improved respectively by 13.3%and 9.87%compared with the conventional GNM.The improved performance of wGNM and fcdGNM was illustrated by using the chain “AA” of the chloroplast ribosome as a case study.
The improved models outperform the conventional GNM in prediction nucleotide fluctuations. Besides that, the nucleotide-specific information was introduced implicitly into the model, which does not increase the calculation burden.Our studies provide two promising candidate models for better revealing the dynamical properties encoded in RNA structures.
- Chinese Physics B的其它文章
- Corrosion behavior of high-level waste container materials Ti and Ti–Pd alloy under long-term gamma irradiation in Beishan groundwater*
- Degradation of β-Ga2O3 Schottky barrier diode under swift heavy ion irradiation*
- Influence of temperature and alloying elements on the threshold displacement energies in concentrated Ni–Fe–Cr alloys*
- Cathodic shift of onset potential on TiO2 nanorod arrays with significantly enhanced visible light photoactivity via nitrogen/cobalt co-implantation*
- Review on ionization and quenching mechanisms of Trichel pulse*
- Thermally induced band hybridization in bilayer-bilayer MoS2/WS2 heterostructure∗

