弥散颗粒型燃料特征线方法输运计算研究

梁越超，宇 炎,*，张 乾，李 颂，梁 亮，赵 强，娄 磊，李满仓

(1.哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001；2.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213)

福岛核事故后，提高核燃料的固有安全特性成为研究热点，以全陶瓷微密封(FCM)燃料[1]和高温气冷堆(HTR)燃料[2]为代表的弥散颗粒型燃料受到国内外研究者的关注。弥散颗粒型燃料对传统中子学计算提出了很大的挑战：1) 弥散颗粒随机分布在燃料中，传统输运方法难以处理没有确定几何描述的介质；2) 弥散颗粒随机分布在基体中形成了一重非均匀性，许多弥散颗粒型燃料堆叠在反应堆堆芯(高温气冷球床堆)，或弥散颗粒型燃料以栅格的形式排列(压水堆FCM燃料)形成了第二重非均匀性。双重非均匀性意味着更加复杂的自屏效应。各国研究者试图将TRISO颗粒弥散所造成的非均匀性等效成均匀燃料问题，以适用于传统的确定论方法及程序，来解决弥散颗粒型燃料的中子学问题。STREAM程序[3-4]采用了缺陷因子法，将包覆层融于基体中以简化为“燃料核-非燃料区”双区问题，失去了计算颗粒各层微观信息的能力。XPZ程序[5-6]同样引入了缺陷因子的概念，理论模型中将颗粒独立，不计颗粒间的相互影响，这导致适用情况需限制在颗粒体积填充率在35%以下。RPT模型[7]将燃料核聚集到弥散介质中心，将颗粒包覆层和基体聚集到燃料之外，形成传统的均匀材料分环问题，但其一般用于燃耗计算。Sanchez-Pomraning方法[8]是一种对弥散介质的直接输运方法。其核心是颗粒与基体间的通量更新方程，将基体与颗粒的空间弦长分布引入到积分输运方程中，用碰撞概率法(CPM)求解更新方程，通过比照均匀问题和弥散问题的角通量解，得到弥散介质的等效均匀化截面，用等效均匀化截面进行输运计算。而后Sanchez等[9]又将Sanchez-Pomraning方法移植到特征线方法(Sanchez-MOC方法)中，MOC可沿不同方向对弥散介质进行特征线扫描，避免了CPM中的各向同性假设。该方法已被应用于DeCART程序[10-11]中。本文基于Sanchez-Pomraning方法开发二维圆柱几何的弥散颗粒型燃料特征线输运程序，并从颗粒填充率、颗粒尺寸及多种颗粒共存问题对Sanchez-MOC方法的精度进行评估。

1 Sanchez-MOC方法

Sanchez-MOC方法是对弥散颗粒介质的直接输运计算方法，作为一种确定论方法并非对弥散介质内的每个颗粒显式建模再对其直接进行特征线输运计算，而是根据理论公式对弥散介质先进行等效均匀化，再使用等效截面和等效源项对均匀化的平源区进行特征线扫描。Sanchez-MOC方法与传统均匀材料MOC相比，弥散颗粒介质输运多了2个维度，一是材料区域细分为颗粒与基体，二是颗粒内部再细分为多层。Sanchez-MOC方法总体上可分为3步：1) 弥散介质等效均匀化过程；2) 对均匀化网格进行改进的特征线扫描；3) 复现颗粒内部各层的标通量。弥散颗粒介质特征线输运主程序流程如图1所示。

图1 弥散颗粒介质MOC输运主程序流程

1.1 等效均匀化模块

Sanchez-MOC方法根据式(1)计算等效均匀化截面，式(2)作为迭代初值。

(1)

(2)

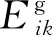
图2 球内逐层间的光学距离

(3)

(4)

(5)

其中：τm为光学距离；Σm为第m层宏观总截面；Rm为第m层的半径；r为当前计算层的半径变量；上标“-”代表中子从第k层飞行第1次到达第l层(跨度较短距离)；上标“+”代表中子从第k层飞行跨过第l层后第2次达到第l层(跨度较长距离)。

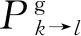
(6)

(7)

其中，Vk为第k层的体积。

2(τk+e-τk-1)]dr

(8)

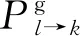
(9)

(10)

等效均匀化模块流程如图3所示。

1.2 Sanchez-MOC方法输运扫描

Sanchez-MOC方法输运计算并非是简单的等效均匀化后直接使用原有输运求解器，Sanchez-MOC方法对原有特征线输运方法进行了改进，但仍保持原有MOC方法框架。在沿特征线段扫描时，先由式(10)计算线段角通量中间变量，用等效截面Σ和等效源项Φas扫描。

Δφ(Ωm)=(φin(Ωm)-Φas)(1-e-ΣL)

(11)

(12)

式中：Δφ(Ωm)为Ωm方向上的角通量增量；φin(Ωm)为沿m方向上的特征线段入射平源区的角通量；L为特征线段长；q0为基体源项；qik为第i种颗粒第k层的源项。

图3 弥散颗粒介质的等效均匀化过程

用中间变量计算平源区出射角通量，因为要保证区域内的产生率与泄漏率守恒，Sanchez-MOC方法比传统MOC多了1个归一化系数，且此归一化系数只用来计算出射角通量，并未影响到累加的平均角通量和之后的标通量：

φout(Ωm)=φin(Ωm)-rcΔφ(Ωm)

(13)

式中：φout(Ωm)为在Ωm方向上弥散网格出射角通量；φin(Ωm)为Ωm方向上弥散网格入射通量；rc为归一化系数。

特征线扫描结束后，角通量累加到网格标通量等特征线计算流程与传统特征线方法无异。

1.3 颗粒内部通量复现

更新方程中的从基体出射角通量到颗粒入射角通量关系式用于复现颗粒内部的标通量。得到的均匀化平源区标通量认为是基体的标通量φ0，借助输运前准备的逃脱概率和碰撞概率复现颗粒内各层的标通量：

(14)

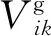
复现出的颗粒通量和基体标通量用于更新各自的裂变源和散射源，通过式(12)计算出等效源项，参与下次特征线扫描。

2 结果验证与评估

本文基于Sanchez-MOC方法和特征线方法组件程序ALPHA[15]实现了计算二维圆柱几何弥散颗粒型燃料功能。本文对程序的计算精度进行验证，比较基准为开源蒙特卡罗程序OpenMC[16]。OpenMC程序使用显式建模方法，蒙特卡罗的基准均为投入粒子数80 000，运行2 000代，舍弃前300代。ALPHA程序为串行CPU版本，运行机器的CPU型号为Intel Core i7 7700HQ (2.8 GHz)。

2.1 单种TRISO颗粒填充问题

问题设置为韩国基于OPR-1000压水堆堆芯的改进款FCM燃料[1]单栅元问题，栅元的几何信息和材料信息列于表1，分别验证不同颗粒填充率和颗粒尺寸对Sanchez-MOC方法精度产生的影响。MOC求解时的燃料区分为5环，气隙与包壳区各分为1环，慢化剂区分为4环。特征线参数为：线宽0.01 cm，极角数3个，辐角数64个。

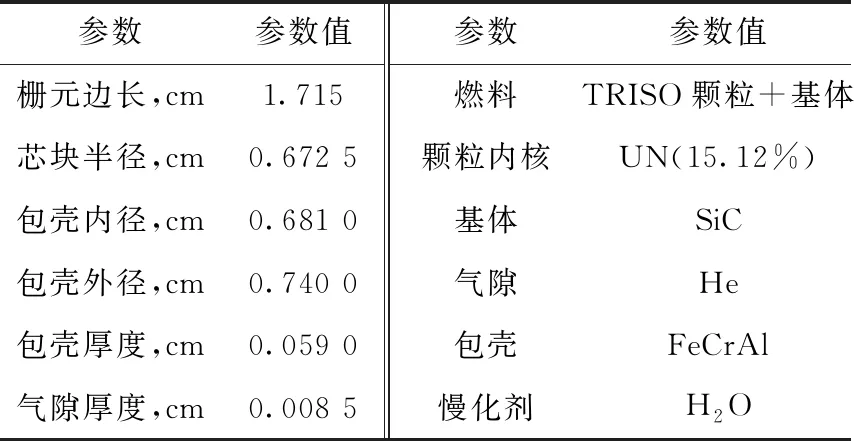
表1 FCM燃料栅元定义

在验证不同TRISO颗粒填充率时，控制TRISO颗粒的分层结构与尺寸不变。TRISO颗粒结构如图4所示。TRISO颗粒尺寸与材料信息列于表2。

图4 TRISO颗粒结构

不同填充率下的Sanchez-MOC方法输运keff解、蒙特卡罗基准解及其蒙特卡罗模拟解的标准差，和ALPHA结果绝对偏差列于表3。由表3可见：TRISO颗粒填充率为15%时，keff绝对偏差达到最大值；在超过1%填充率的范围内，keff绝对偏差总体呈下降趋势，在50%填充率下的绝对偏差只有9.32 pcm。计算效率方面，50%填充率的计算时间远大于其他填充率，其中等效截面迭代时间为334.0 s，且等效截面的迭代次数随填充率的升高而增大，当填充率超过50%时Sanchez-MOC方法的等效截面很难收敛。填充率在1%～50%范围内的Sanchez-MOC方法计算结果未出现极端偏差情况，均可得到符合作为输运求解器要求的计算精度。

表2 TRISO颗粒几何与材料定义

固定颗粒填充率为20%、颗粒半径为0.03～0.075 cm时，验证不同颗粒尺寸条件下Sanchez-MOC方法的计算精度。根据FCM燃料的设计报告，TRISO颗粒尺寸中缓冲层、热解碳、陶瓷层的厚度均保持不变，而燃料内核的半径可根据需要在一定范围内变化，颗粒具体尺寸列于表4。

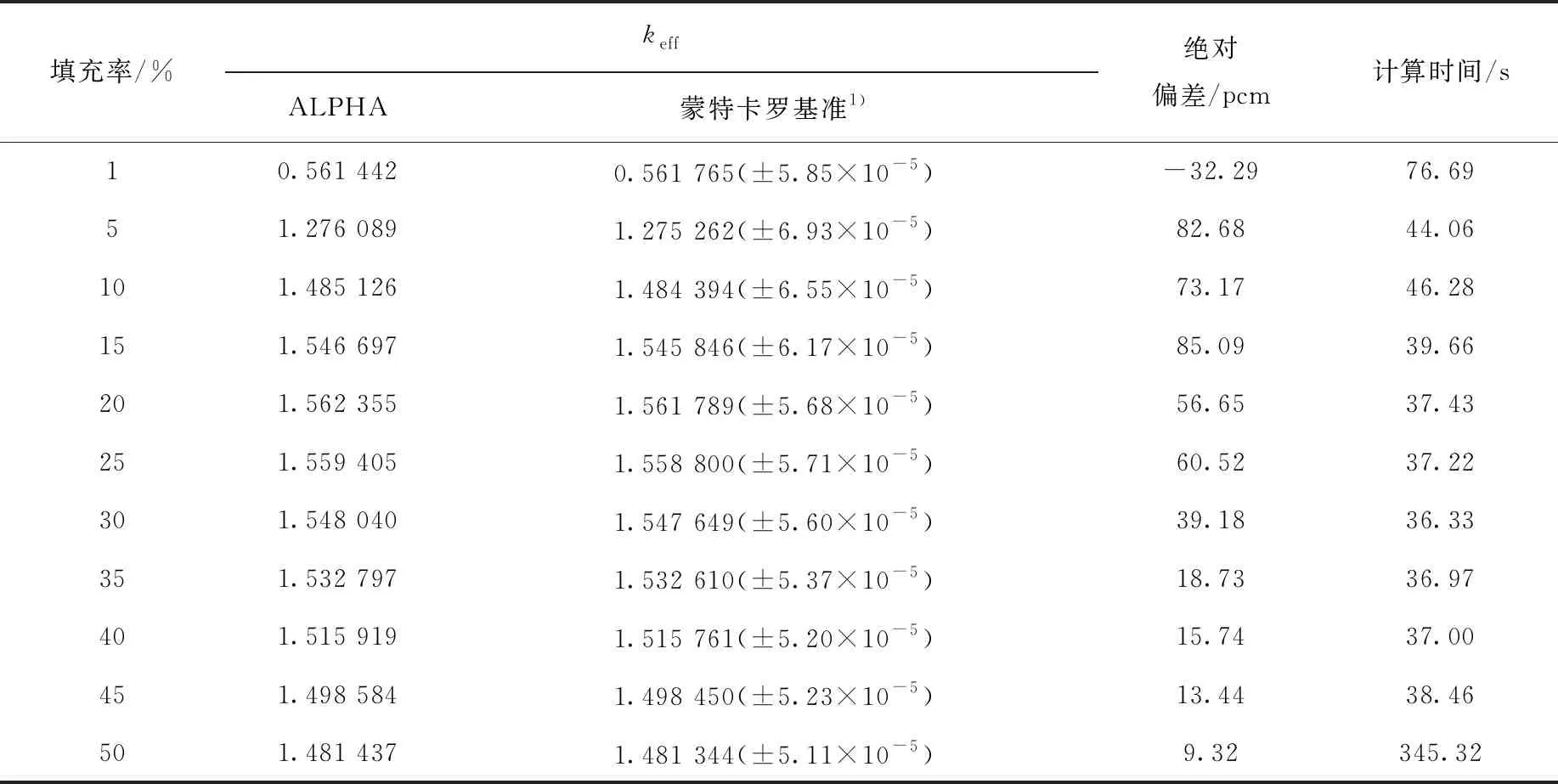
表3 不同填充率下Sanchez-MOC方法的计算结果

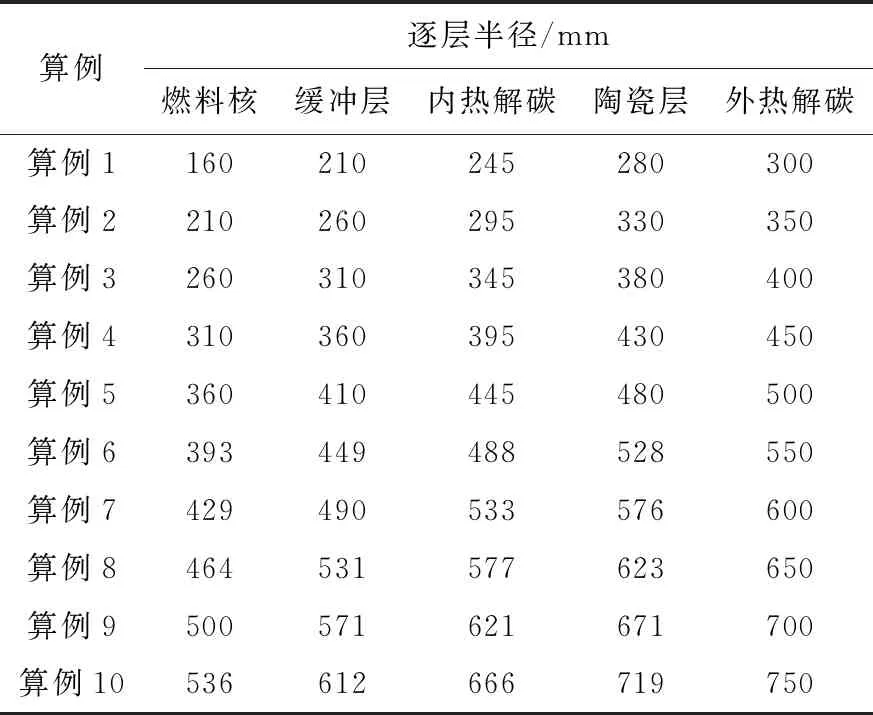
表4 验证颗粒的尺寸

不同颗粒尺寸下的Sanchez-MOC方法输运keff解、蒙特卡罗基准解和绝对偏差列于表5。由表5可见，Sanchez-MOC方法在不同颗粒尺寸下的keff绝对偏差均在50～75 pcm之间波动，过大或过小尺寸的TRISO颗粒均未引起Sanchez-MOC方法产生异常精度偏差。这说明使用Sanchez-MOC方法进行FCM燃料设计时计算精度不会受颗粒尺寸的影响。

2.2 带毒物颗粒填充问题

带毒物颗粒填充问题主要是为验证Sanchez-MOC方法对多种颗粒共存情况的适用性，验证采用了3种毒物颗粒，分别为含B4C的BISO颗粒、含Er2O3的BISO颗粒和含Gd2O3的QUADISO颗粒，3种毒物颗粒和共存的TRISO燃料颗粒的几何参数列于表6。本文验证了3个算例，填充率信息列于表7。

表5 不同颗粒尺寸下的Sanchez-MOC方法计算结果

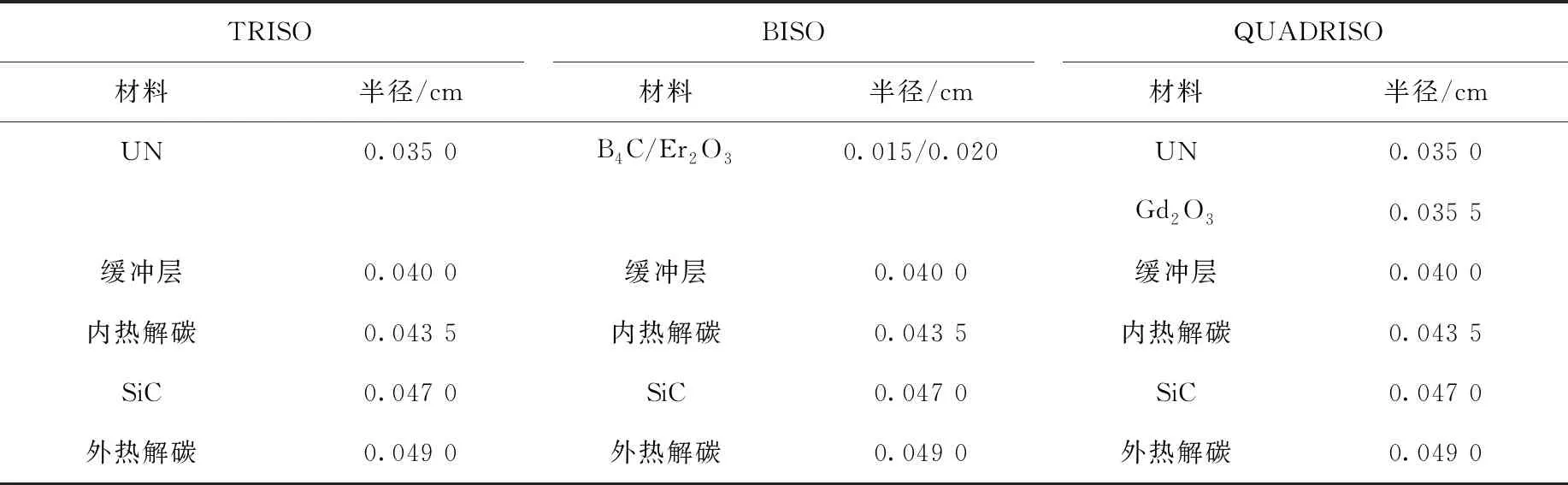
表6 燃料颗粒与毒物颗粒的几何参数

表7 带毒物颗粒问题验证算例

有效增殖因数结果列于表8，两种双颗粒共存问题绝对偏差均在31 pcm以内，QUADRISO颗粒单独填充的问题绝对偏差较大为-163.22 pcm，且该绝对偏差无法通过加密颗粒内部分层来降低。计算结果表明，Sanchez-MOC方法可计算多种颗粒并存问题，且没有因颗粒种类的变多绝对偏差变大，符合对特征线输运求解器的精度要求。

表8 带毒物问题的验证结果

2.3 颗粒与基体通量分布验证

基于30%填充率的TRISO颗粒填充问题，将Sanchez-MOC方法复现出的颗粒内燃料核标通量及基体标通量与OpenMC程序统计出的UN材料通量、基体材料标通量相比较，验证Sanchez-MOC方法复现颗粒与基体标通量的准确性，同时也比较了Sanchez-MOC方法的等效均匀化截面与OpenMC程序统计的弥散介质总截面，结果如图5所示。

结果显示，Sanchez-MOC方法通过迭代过程得到的等效截面与实际弥散介质内的总截面十分接近，最大相对偏差仅为0.17%，证明等效截面可用于特征线扫描。Sanchez-MOC方法得到的基体标通量比复现出的颗粒内燃料核的标通量更加准确，复现出的燃料核通量最大相对偏差为0.69%。燃料核的热群通量偏差明显高于快群与共振群，而且偏差并非等效截面引起，因为燃料核的热群截面较快群及共振群大得多，热群的平均自由程较小，一定程度下不符合颗粒通量复现时的颗粒内中子各向同性假设，最终体现在颗粒内核的通量偏差上，但Sanchez-MOC方法复现出的颗粒内部通量也满足了精度要求。

3 结论

本文基于Sanchez-Pomraning方法编写了二维圆柱几何的特征线输运计算程序，实现了对弥散颗粒型燃料的直接输运求解，可解决颗粒内分多层、多种颗粒共存等弥散颗粒燃料问题。同时验证了该程序在不同颗粒填充率、不同颗粒尺寸、燃料颗粒与毒物颗粒共存问题的精度表现，程序在1%～50%填充率、颗粒直径小于0.15 cm等情况下的绝对偏差均小于100 pcm，在TRISO燃料颗粒与可燃毒物颗粒共同填充燃料棒情况下的表现较好，在填充QUADRISO毒物颗粒情况下绝对偏差较大，但也仅有163 pcm。经过验证，Sanchez-Pomraning方法复现出的颗粒内部标通量与基体标通量也十分精确，可供下一步精细燃耗计算、毒物燃耗计算的要求。Sanchez-Pomraning方法是解决弥散颗粒型燃料输运计算的有效方法。