超临界二氧化碳在印刷电路板式换热器内的流动换热特性研究
徐 哲,张明辉,段天应,付 文,李秋龙,李培跃
(洛阳船舶材料研究所,河南 洛阳 471023)
随着世界能源消耗量的增加及能源结构的调整,第4代核反应堆系统受到了极大的关注[1]。目前,传统的郎肯循环仍是核反应堆系统中应用最广泛的动力循环。与朗肯循环相比,超临界二氧化碳(SCO2)布雷顿循环系统能提高热效率,减少设备投资。超高温气冷堆和钠冷快堆可与SCO2布雷顿循环系统相结合[2-4]。SCO2布雷顿循环系统中的回热器、预冷器等换热器是系统的关键设备之一,其安全性能和换热效率直接影响整个系统的安全性和效率[5]。由于空间的限制及设备较高的运行温度和压力,传统管壳式换热器和板式换热器难以满足需求,需要采用耐高温、高压的紧凑式换热器。
印刷电路板式换热器(PCHE)是一种微通道换热器,其流体通道是在金属板片上采用光化学蚀刻技术加工形成的,通道截面以mm级的半圆形结构为主。与传统换热器相比,PCHE具有换热效率高、耐低温高温(-196~900 ℃)、耐高压(60 MPa)等优点。与同等热负荷的传统管壳式换热器相比,PCHE的体积和质量可减少85%以上[6]。PCHE在海洋油气处理平台[7]、核能[8-9]、光热发电[10]、氢能源[11]等众多行业都具有十分广阔的应用前景。
流动换热特性是PCHE热工设计的基础。目前,国内外针对PCHE的流动换热特性开展了大量研究。Nikitin等[12]进行了PCHE的流动换热实验,并根据实验结果拟合了传热和压降的经验关系式;Kim等[13]利用氦循环实验台架,测试了层流区域氦气的流动换热性能,同时结合数值模拟结果进行了分析;Kim等[2]采用数值模拟方法研究了zigzag流道内部SCO2的流动换热;Yoon等[14]采用数值模拟方法研究了层流时不同zigzag角度对氦气流动换热的影响。Kruizenga等[15]测量了拟临界温度附近SCO2的传热性能,发现在拟临界温度附近,由于Pr增加,传热系数激增,并采用数值模拟进行了验证分析。Ren等[16]采用数值模拟方法研究了PCHE流道内部的强制对流换热及混合对流换热,并对传热中热物理性质及浮升力的影响进行了分析,提出了传热关联式。Chen等[17]实验测量了PCHE的稳态传热,并结合数值模拟结果得到了相应的传热关联式。Seo等[18]实验测量了低雷诺数下PCHE的传热特性,并分析了顺流和逆流对传热的影响。Ngo等[19]采用数值模拟的方法计算了SCO2在S型流道内的流动换热特性。
在拟临界温度附近,SCO2的物性变化较为剧烈,导致其流动换热规律十分复杂。为此,本文采用数值模拟方法,研究SCO2在拟临界温度附近的流动换热特性。
1 数值模型
1.1 物理模型
PCHE冷热侧换热板片交错排列,具有周期性的特点,为了减小计算量,本文采用周期性边界条件,模拟1组冷热流道的对流换热,如图1所示。建立的流道总长度为700 mm,中间500 mm设置为换热段,前后各100 mm设置为绝热段。上侧流道为热工质SCO2,下侧流道为冷却水,冷热流体逆流换热。建立的模型尺寸参数为:板厚,1.5 mm;流道直径,1.5 mm;节距,2.4 mm;水力直径,0.916 mm。
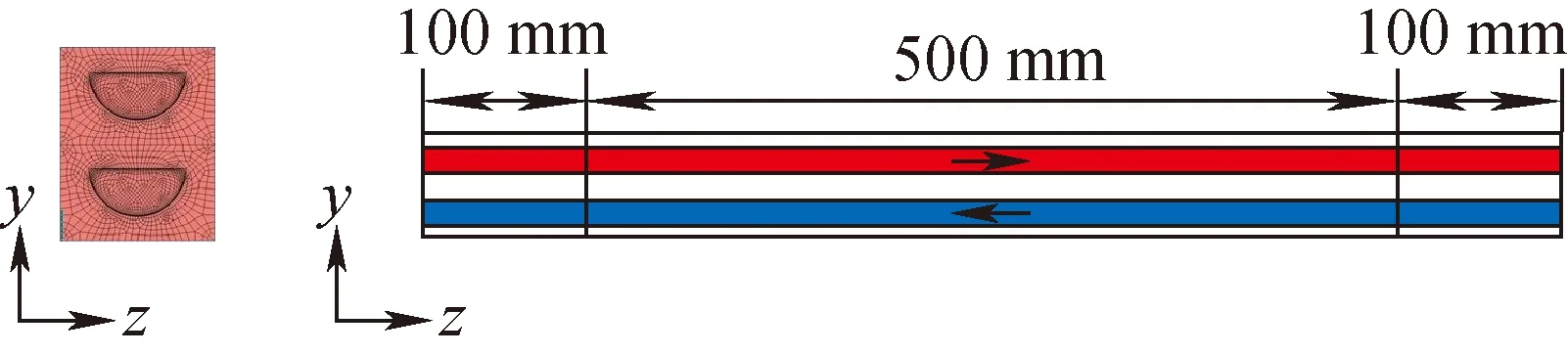
图1 数值模拟模型
为更好地计算近壁面区域的流动换热特性,对壁面处的网格加密,以保证壁面附近y+小于1。数值模拟软件采用FLUENT 18.0。湍流模型采用SSTk-ω模型,压力和速度离散方法采用SIMPLEC算法,变量梯度采用Least Squares Cell Based方法求解,压力插值采用Standard,其余控制方程采用二阶迎风格式离散。模型的上、下壁面设置为周期性边界条件,其余壁面设置为绝热边界条件,流体与固体接触的壁面设置为耦合传热边界条件。冷、热流体进口设置为质量流量进口边界条件,出口设置为压力出口边界条件。SCO2的物性采用FLUENT的real gas model,该模型引用了美国国家标准技术研究所提供的SCO2的物性参数。
1.2 模型有效性验证
Kruizenga等[20]实验测量了直通道内SCO2的流动换热,其实验装置通道半径为0.95 mm,传热段长度为500 mm。为测量SCO2温度分布,将实验装置分成了10段,每个传热段长度为50 mm。通过热量平衡的方法,测量了压力为7.5 MPa、流量为326 kg/(m2·s)时每个传热段的平均壁面温度。为验证数值模拟的可靠性,本文对Kruizenga等的实验模型进行了建模,如图2所示。中间500 mm为传热段,在传热段前后各设置500 mm的绝热段。进行验证时,流体入口的温度与压力和实验保持一致,采用UDF将实验测得的壁面温度施加在模型的壁面上作为边界条件。其余设置和1.1节相同。实验和数值模拟得到的传热段流体平均温度如图3所示。由图3可见,数值模拟结果与实验结果吻合较好,证明了本文建立的模型及采用的计算方法是有效的。

图2 Kruizenga实验段的物理模型
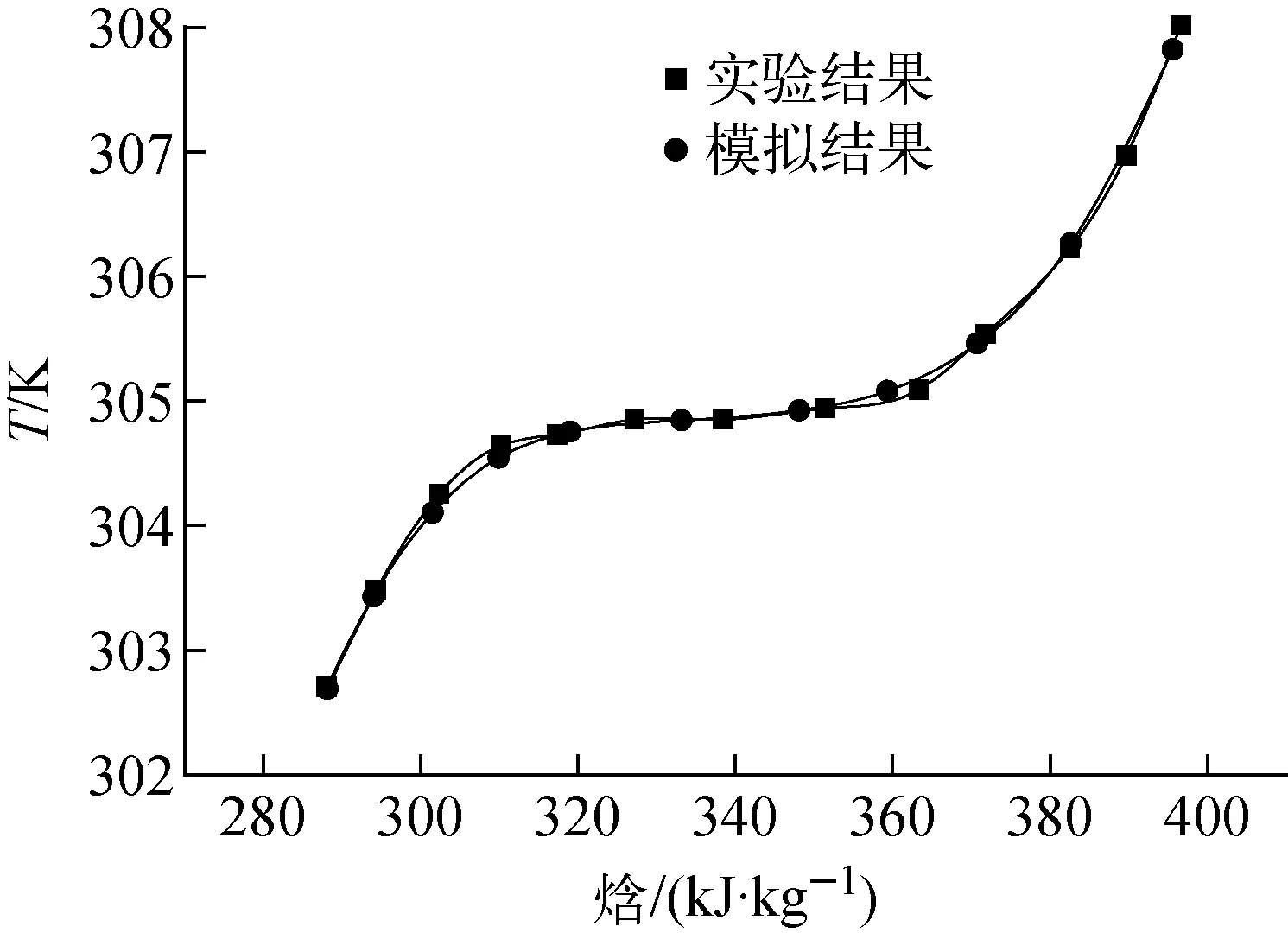
图3 传热段SCO2温度实验结果与模拟结果对比
1.3 数据处理
通道的水力直径Dhyd为:
(1)
雷诺数Re为:
(2)
传热努塞尔数Nu为:
(3)
对于冷热流体,热流体热负荷Qh和冷流体热负荷Qc分别为:
Qh=hhAh(Th,b-Th,w)
(4)
Qc=hcAc(Tc,w-Tc,b)
(5)
总传热量Q为:
Q=UAΔT
(6)
对于本文建立的模型,由于冷热侧流道是相同的,因此A=Ah=Ac。
对数平均温差ΔT为:
(7)
导热热阻rw为:
(8)
(9)
式中:下标h表示热流体,c表示冷流体,w表示壁面处,b表示流体处,o表示流体出口处,i表示流体入口处;D为流道直径,m;u为流体速度,m/s;ν为运动黏度,m2/s;h为对流换热系数,W/(m2·K);λ为导热系数,W/(m·K);U为总传热系数,W/(m2·K);A为传热面积,m2;T为流体截面平均温度,K;t为冷热侧流道壁面间距,m。
1.4 网格独立性分析
为了保证模拟结果的准确性,确保计算结果与网格数量的无关性,本文建立了3种不同的网格,网格数量分别为51万、102万、184万。在保证其余设置相同的情况下,分别进行了数值模拟,得到热负荷Q的变化和热流体侧壁温Tw的变化,如图4所示。
以网格3为基准,对于网格1,Q和Tw的相对误差分别为4.5%和0.004%;对于网格2,Q和Tw的相对误差分别为0.3%和0.003%。综合考虑计算精度与计算时间,本文选取网格2进行计算分析。
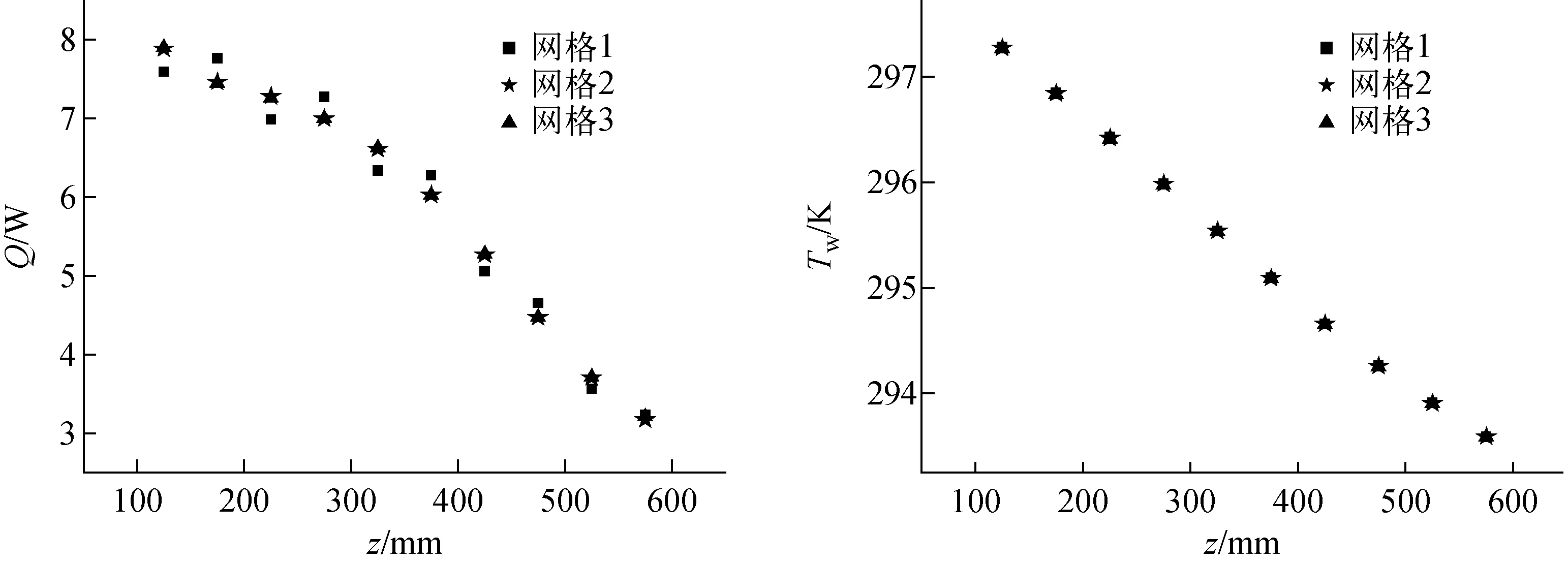
图4 网格无关性分析
2 数值模拟结果分析
2.1 沿流动方向传热分析
图5为SCO2沿流动方向的温度分布。为更直观比较,图5中相邻两条等温线之间的温差相等。沿流动方向,当SCO2截面平均温度Tf下降至拟临界温度Tpc时,流体中心区域温度梯度下降;当Tf降至小于Tpc时,流体中心区域温度梯度开始增加。当Tf继续下降且小于某一温度T1时(T1位置示于图6),温度梯度又逐渐下降。

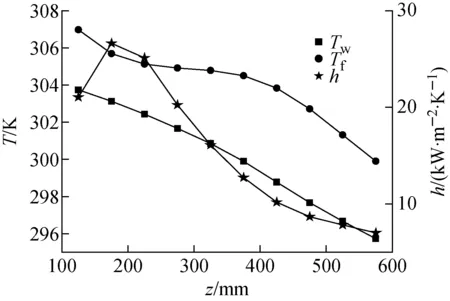
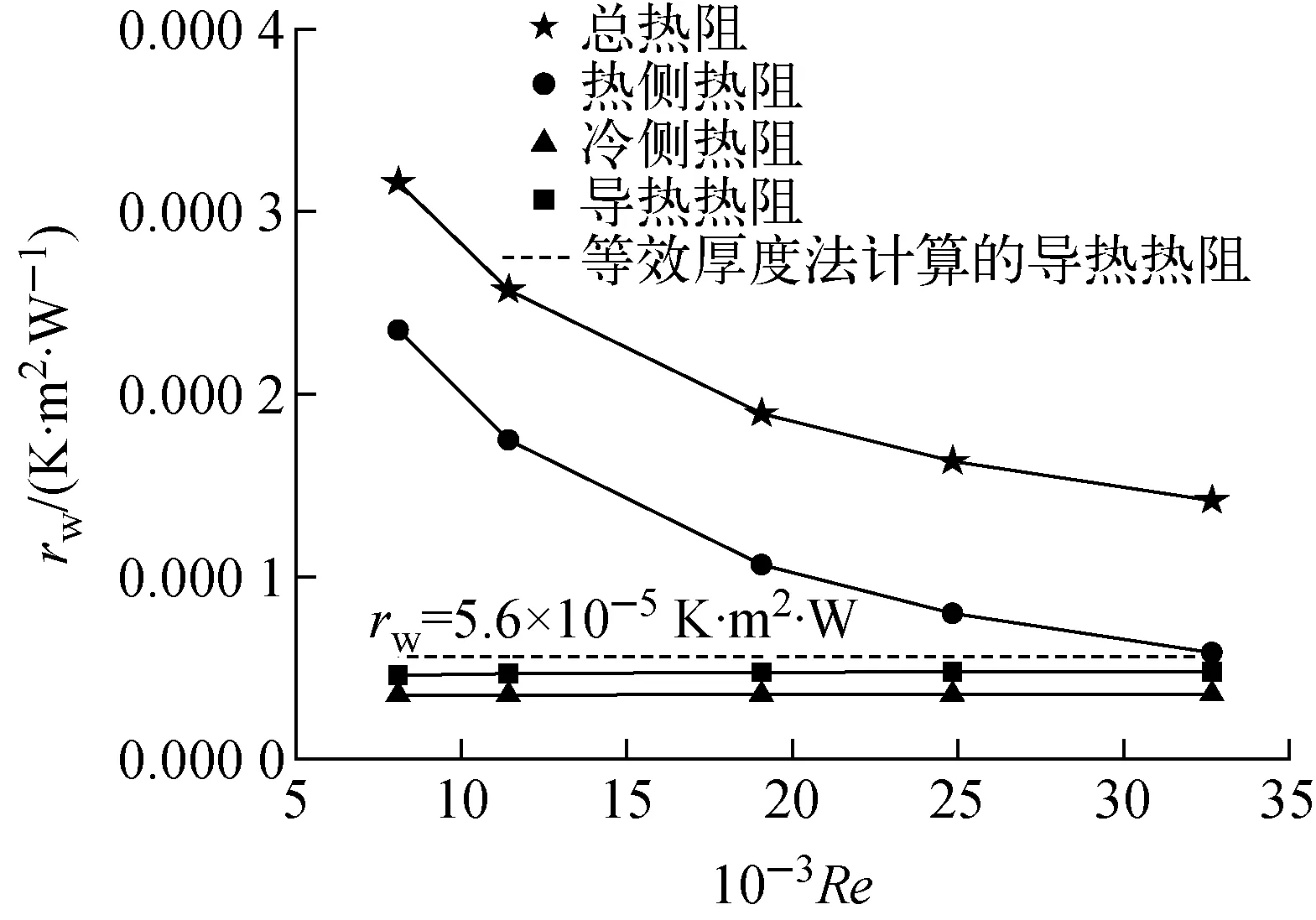
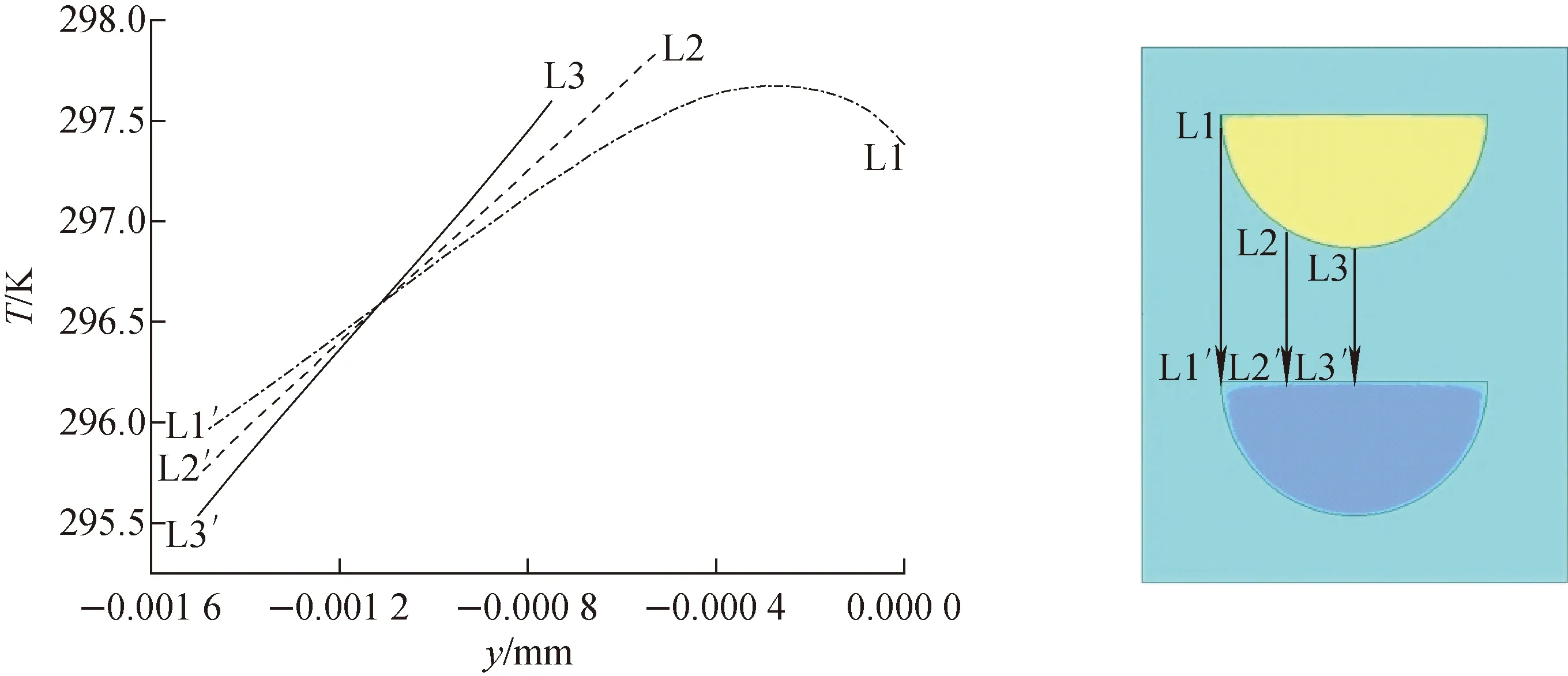
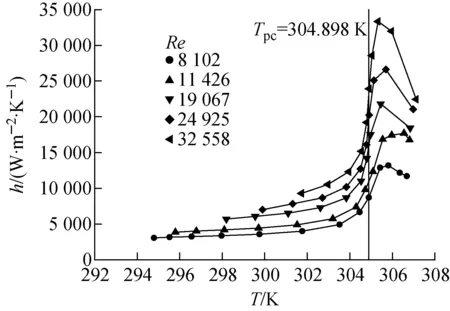
a——Tf >Tpc;b——Tf =Tpc;c——T1 上述温度梯度的变化可采用有效导热系数来解释。有效导热系数λeff的定义[21]为: (10) 式中:λt为湍流导热系数,W/(m·K);cp为比定压热容,J/(kg·K);μt为动力黏度,Pa·s;Prt为普朗特数。 计算得到的有效导热系数如图6所示。由图6可见,沿流动方向,在z<300 mm阶段(对应Tf>Tpc),λeff增加;在z=300 mm处(对应Tf=Tpc),λeff最大;在z>300 mm阶段(对应Tf 图6 λeff沿流动方向的变化 SCO2的平均温度Tf、壁面温度Tw及对流换热系数h沿流动方向的变化如图7所示。由图7可见,沿流动方向,SCO2的流体平均温度、壁面温度均不断减小。沿流动方向,在SCO2平均温度大于拟临界温度的阶段,流体平均温度下降,密度增加,流速减小,黏度增加,对换热产生削弱;然而,由于流体导热系数和比热容的增加,强化了换热,克服了黏度增加对换热削弱的影响,对流换热系数增加;在SCO2平均温度小于拟临界温度的阶段,流体平均温度继续下降,密度增加,流速减小,导热和比热容减小,黏度增加,抑制了换热,对流换热系数逐渐减小。由图7还可见,SCO2的对流换热系数在其温度降至拟临界温度之前达到了最大值,这是因为在流体近壁面区域,流体平均温度与壁面温度更为接近,传热受到了近壁面区域流体的热物理性质的影响[12]。 图7 SCO2的平均温度、壁面温度及对流换热系数沿流动方向的变化 图8 热阻随Re的变化 通过改变SCO2的质量流量,计算了不同Re下的导热热阻,如图8所示。由图8可见,热侧SCO2的对流换热热阻在总热阻中占比最大,当Re为8 102时,其占比为74.4%。随着Re的增加,热侧对流换热热阻逐渐减小,其在总导热热阻中所占比例逐渐减小,当Re为32 558时,其占比减小到41.2%。冷侧水的对流换热热阻最小,小于中间固体金属的导热热阻。因此,在进行换热器的热力设计时,如水为冷侧工质,则需考虑导热热阻的影响。由于导热热阻只与固体壁面的几何形状和固体的热物理性质有关,因此对于本文的模型其应为一确定值。本文计算得到的导热热阻为4.8×10-5K·m2/W。 由于PCHE冷热侧流道之间的间距是变化的,导热热阻无法直接采用式(9)进行计算。Kim等[15]采用等效厚度法计算导热热阻,其将冷热侧流道之间的间距简化为一确定的值: (11) 式中:te为等效厚度;t为板片厚度;d为流道直径。 利用等效厚度法计算得到的导热热阻为5.6×10-5K·m2/W,略大于本文模拟得到的导热热阻,两者之间的相对误差为14.3%。因此,在设计过程中采用等效厚度方法计算导热热阻是偏保守的。 上述等效厚度法假设固体内部温度呈线性分布。图9为z=300 mm截面处固体内部y方向温度的分布。由图9可见:在中间区域沿直线L3-L3′,固体内部的温度呈线性分布;离流道中心越远,线性度越差;由于在流道拐角处传热效果较差,沿直线L1-L1′,温度分布的线性度最差。因此,传热壁面之间温度的非线性分布导致了等效厚度法计算的热阻和模拟热阻之间存在误差。 通过改变SCO2的质量流量,对不同工况下流道内部SCO2的换热特性进行了计算和分析。 图10示出不同Re下SCO2的对流换热系数的变化。在不同Re下,对流换热系数均随流体平均温度的增加先增加,在拟临界温度附近达到峰值,随后逐渐减小。对流换热系数达到峰值时,流体的平均温度均略大于拟临界温度。随Re的增大,对流换热系数最大值与流道入口处对流换热系数的比值增大(表1)。表明Re越大,在拟临界温度附近换热强化的程度越大。随Re的增加,流体的湍流强度增加,换热能力也随之增强。 图9 y方向温度的分布 图10 不同Re下的SCO2的对流换热系数 表1 不同Re下换热强化程度对比 本文采用数值模拟的方法,计算分析了跨拟临界温度SCO2的流动换热特性,得出结论如下。 1) SCO2的温度梯度的变化与有效导热系数变化趋势一致。 2) SCO2对流换热系数最大值出现时,流体平均温度大于拟临界温度。 3) SCO2侧对流换热热阻在总热阻中占比最大,其次为导热热阻,最小的为水侧对流换热热阻。随Re的增加,SCO2侧对流换热热阻逐渐减小,其在总热阻中所占比例逐渐减小;等效厚度法计算的导热热阻比模拟结果略大,原因是传热壁面之间温度呈非线性分布;采用等效厚度法进行设计计算,结果偏保守。 4)Re越大,在拟临界温度附近换热强化的程度越大。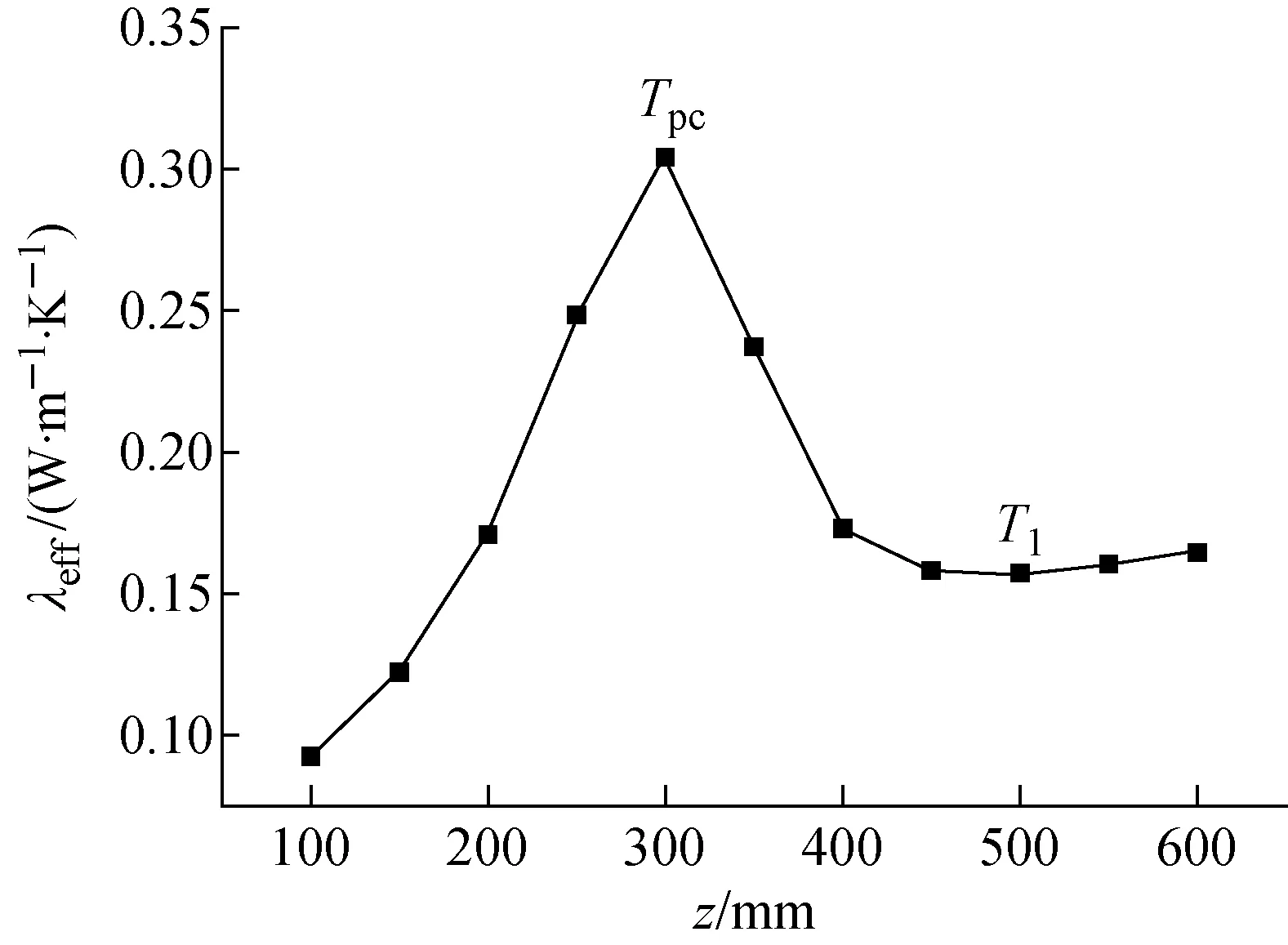
2.2 导热热阻分析
2.3 Re对换热的影响

3 结论

