高雷诺数下电蓄热锅炉内螺纹管换热计算与分析
付江奇,王启民,王国峰
(沈阳工程学院a.研究生部;b.能源与动力学院,辽宁 沈阳 110136)
近年来,内螺纹管作为一种高效换热部件,以其传热效果良好,制造工艺简单的优点,在空调制冷[1]以及石油化工管道输运[2]等领域均有广泛应用,其三维剖面结构如图1 所示,内螺纹管外表面光滑,内壁采用一定加工工艺形成的具有一定螺旋角度的翅片。实践证明[3-4],这种特殊结构具有很好的强化换热性能,流动阻力的增加也十分有限。因此,以某高校电蓄热锅炉的某常见型号内螺纹烟管为研究对象,以高温空气为换热介质,在高雷诺数条件下研究其对流换热特性。
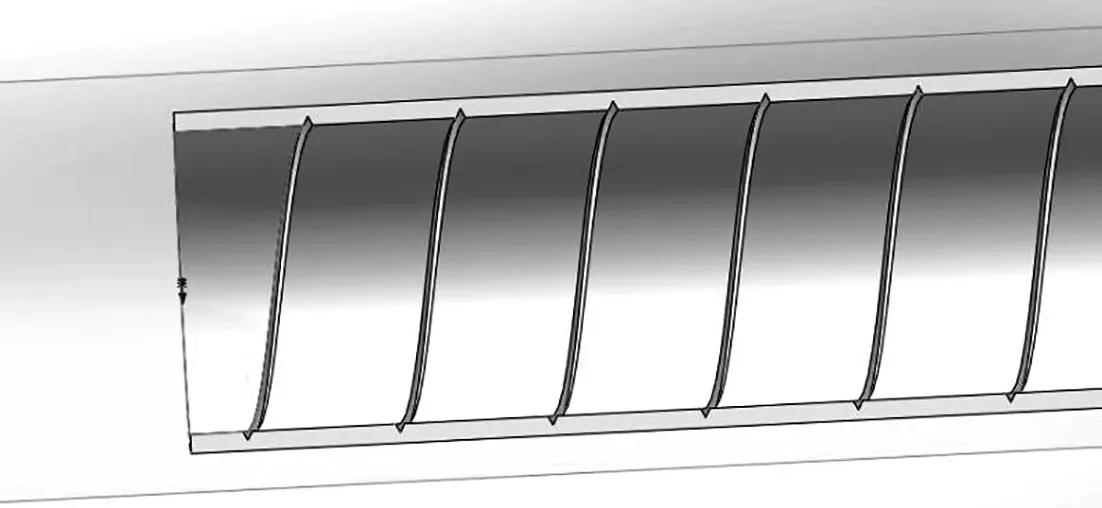
图1 常见内螺纹管的三维剖面结构
1 经验公式的选取与换热计算
1.1 经验公式的选取
选取内径d=45 mm 的某常见型号螺纹管作为电蓄热锅炉主要换热元件。为了进一步探究内螺纹管的换热特性,在确定相关螺纹参数的前提下,以高温空气为流动介质并定义其温度T和雷诺数Re的范围:673 K ≤T≤1 073 K,4×104≤Re≤1.6 ×105。综合上述基本条件,查找相关文献并借鉴近半个世纪国内外相关研究理论成果[4-9],最终筛选出两组可用于电蓄热锅炉内螺纹管实际换热计算的经验公式,即东南大学公式[3]和重庆大学公式[9]。
1)东南大学公式
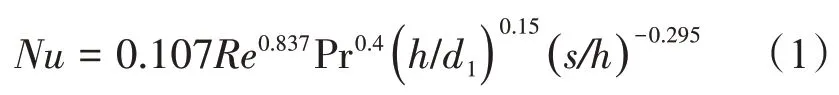
式 中,h/d1=0.02~0.05,s/h=11~25,104<Re<105。
2)重庆大学公式
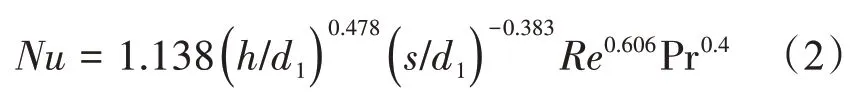
式中,s/d1=0.5~1.7,h/d1<0.07,2 × 104<Re<7 × 104。
1.2 换热计算
针对经验公式中的普朗特Pr 项,选取冯俊凯[10-19]等人研究的空气平均热容量、运动粘度、导热系数等试验关联式,对式(1)进行代入、整理、计算,计算结果如表1所示。

表1 对流换热系数a的部分计算结果 kW/(m2·K)
2 ANSYS FLUENT 数值模拟与理论计算对比
2.1 ANSYS FLUENT数值模拟
为了验证理论计算结果的可靠性以及经验公式的适用性,通过ANSYS ICEAM 建立比例为1:1的内螺纹管模型并进行网格划分,然后导入ANSYS FLUENT中。设置空气入口温度为673 K,内螺纹管壁面温度为473 K,平均温度为573 K,螺纹管入口流速分别设定为43 m/s、54 m/s、65 m/s、76 m/s、86 m/s、97 m/s、108 m/s、118 m/s、130 m/s、140 m/s、151 m/s、162 m/s、173 m/s,进行流体模拟,所得部分模拟结果如图2所示。
图2 不同空气入口流速对应的出口平均流量、温度及速度值
2.2 经验公式计算与数值模拟对比结果
利用ANSYS 模拟结果分别与两组经验公式在相同工况条件下进行比对,结果如表2 和表3所示。
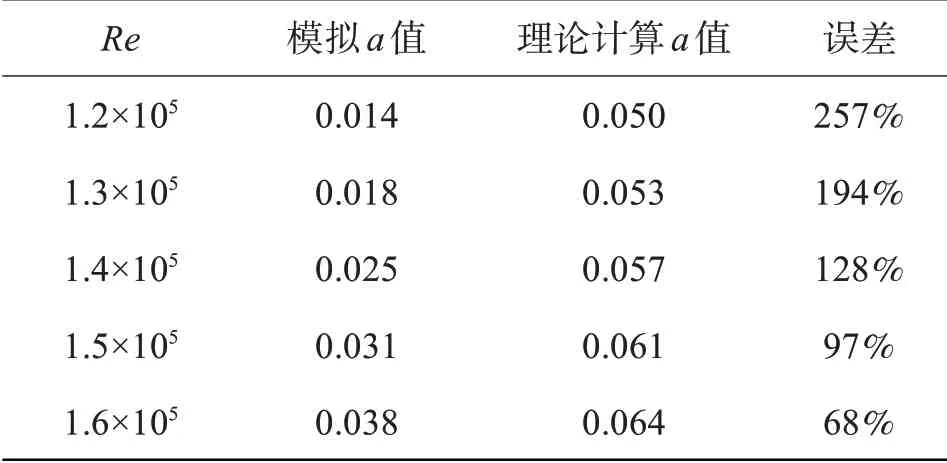
表2 利用式(1)所得部分模拟数值与理论计算对比结果
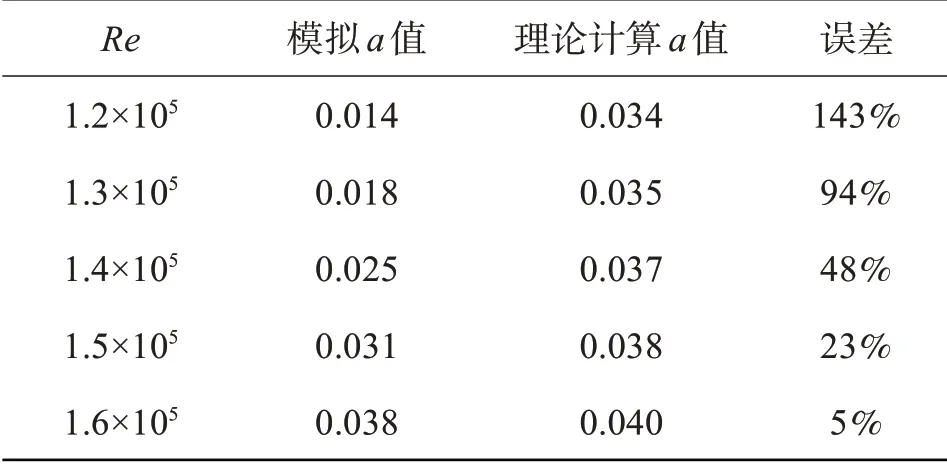
表3 利用式(2)所得部分模拟数值与理论计算对比结果
通过对比可以发现,计算结果与模拟结果均存在一定地误差。由表3可知,随着雷诺数Re不断增大,误差值由143%下降至5%,且在5 个误差值中有2 个误差值在30%以内。当雷诺数Re=1.6×105时,误差值为5%,说明应用式(2)所得出的换热系数a更接近实际内螺纹管的运行工况。
3 对比结果分析
通过经验公式在相同工况下的计算结果与数值模拟之间的对比可知,式(2)误差较小,更适用于电蓄热锅炉内螺纹管的换热计算,但其部分结果仍高于工程计算给出的一般误差范围(30%左右),产生此结果的原因如下:
1)烟气的雷诺数Re范围(4×104≤Re≤1.6 ×105)远超出经验公式给出的理论适用范围,同时在选取经验公式进行具体计算时,采用了部分湿空气热力试验关联式代替烟气Pr经验值,最终导致换热系数的数值普遍偏大。
2)在使用FLUENT 软件模拟内螺纹管烟气流动时选用k-ε模型,该模型默认流体涡粘性系数εm为标量值,但管内高雷诺数下的湍流运动使得εm对方向很敏感,进而导致原湍流动能输运方程更加复杂,理论上需要建立雷诺应力与湍流动能k之间的关系进行封闭求解。由此可见,k-ε模型对于一般的三维流动甚至更复杂的高雷诺数湍流流动存在一定的局限性,这也是造成模拟计算结果对比出现较大误差值的重要原因。
3)在ANYSYS FLUENT 软件模拟工况的边界条件设置上,采用简单对数平均温度作为内螺纹管的表面温度,而忽略了湍流流动的复杂性以及在纳维-斯托克斯方程中运用了温度函数u随空间点位置不同而变化的事实。这也在一定程度上影响了模拟结果的可靠性。
4 结论
1)在高雷诺数(4×104≤Re≤1.6×105)及相同工况条件下,以高温空气为介质,通过对比换热系数a的计算值与模拟值,确定了重庆大学经验公式更符合电蓄热锅炉内螺纹烟管的换热计算。
2)针对理论计算与模拟对比结果中存在的较大误差的情况,对其进行了分析和探究,并在内螺纹管的相关热力计算中进一步修正,取得了较为理想的结果。

