基于门控递归单元神经网络的风速误差修正模型短期风电功率预测

（国网辽宁省电力有限公司 盘锦供电公司，辽宁 盘锦 124000）

目前，风能已经成为第二大可再生能源，被广泛应用于诸多领域［1］。然而，风能所具有的间歇性和波动性也给电网调度和电力交易带来了巨大的挑战［2］。在风量日益增长的情况下，及时准确地预测风电功率，能够有效地减轻间歇性和波动性对电网所带来的不良影响。风电功率预测从时间尺度上划分可分为4 类，分别为超短期（分钟～小时）、短期（小时～天）、中期（周～月）、长期（月～年）。其中，超短期和短期风力发电预测为电网调度和电力交易提供了基础；长期风力发电预测对选址、性能预测、风车规划以及为特定地点选择最佳风力发电机尺寸具有重要意义［3］。本文主要研究的是未来24 h 内的短期风电功率预测，用预测结果来辅助电网调度和电力交易。

在国内外所提出的风电功率预测方法中，主要利用两种类型的数据来建立风电功率预测模型，一种是风电功率历史数据，另一种是数值天气预报（NWP）数据。风电功率历史数据主要用于超短期风电功率预测［4］。由于风的功率会直接受到风速立方的影响，所以NWP 数据是风电功率预测的重要数据源。NWP 所提供的风速主要被用于建立短期风力预测模型。现有的利用NWP数据进行风电功率预测建模的方法可分为统计方法、人工智能学习方法和混合方法［5］。然而，风速的间歇性和波动性也同样会导致NWP数据所提供的风速具有不确定性，进而影响了风电功率预测的准确性，这给风电功率预测带来了巨大的挑战。因此，利用数据挖掘方法对NWP数据进行处理才能更加充分地利用风速序列［6］。数据挖掘的方法有很多种，例如人工神经网络结合计算流体力学、日相似聚类、希尔伯特-黄变换和主成分分析，应用这些方法能更有效地对短期风电功率进行预测。除此之外，也可以利用高斯过程和稀疏贝叶斯学习来建立风力发电预测模型。在文献［7］中，利用边界层标度法预测长期平均近地面的风功率。然而，NWP 中的风速数据总是存在误差，因此扩展数值天气变量和偏差校正方法也常被用于校正风电功率预测中的NWP 风速。

为了提高风电功率预测的准确性，国内外的研究人员提出了多种误差修正模型［8］。但是，这些误差校正模型是为了提供点对点的预测而建立的，其预测过程并不使用NWP气象数据和风电功率时间序列的特征参数。研究者提出了基于功率时间序列的识别方法和校正方法，以此来实现提高效益和削减成本的目的。此外，也可以利用矢量误差校正模型来校正风速时间序列的误差［9］。综上所述，可以利用NWP风速误差的时间序列特征来建立误差修正模型，从而提高风电功率预测的精度。

由于时间序列模型会受到时间序列特征的影响，所以时间序列特征的提取变得非常重要。时间序列特征的提取方法也因此被广泛研究，如时间序列-特征直方图方法、时间重要性曲线、空间聚集距离、小波主成分分析、基于加权形状的时间序列聚类、相似形状函数时间序列预测器、监督聚集特征提取方法，以及形状感知时间序列匹配算法。尽管有如此多的时间序列特征提取方法，但是都没有将时间序列的统计学应用到时间序列的提取中。综上所述，现有的统计模型或时间序列模型都没有充分利用统计特征和时间序列特征来校正NWP风速时间序列。递归神经网络（RNN）经常被用于处理不同领域的时间序列。门控递归单元（GRU）是RNN 的一种变体，被认为是长短期记忆神经网络的简单版本。利用门控递归单元神经网络，可以充分利用时间序列的统计特征和动态时间行为。GRUNN 与传统神经网络的最大区别是引入了GRU 来克服一些缺点，其隐含层的门控单元结构可以有效地缓解梯度消失和梯度爆炸问题［10］。因此，该神经网络具有修正NWP 风速误差的能力［11-12］。

1 问题描述和预测框架

本节描述了利用数值天气预报NWP 的风速进行风力发电预测的问题，然后对NWP 风速的特点进行分析，进而提出了风电功率预测的模型框架。

1.1 问题描述

在自然界中，风速是一个连续的物理量。本文利用风速塔在一小段时间间隔（如1 s）内测量风速，得到风速时间序列，然后计算实测风速的平均值，得到较大时间间隔（如15 min）的风速时间序列。

图1 为某实际风电场实测风速与风力功率的关系，满足风力机功率曲线。风力涡轮机捕捉风能并将其转化为电能，风力涡轮机的输出功率与通过叶片有效面积的空气的动能有关。输出功率如下：

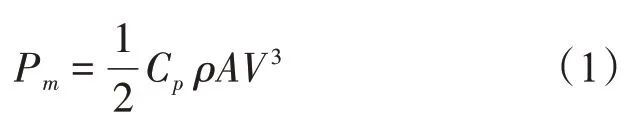
式中，Pm为风力机输出功率；Cp为风力机功率系数；ρ为空气密度；A为风力机叶片扫过的面积；V为风速。

由于NWP 的不确定性，其风速存在误差ε，故式（1）变为

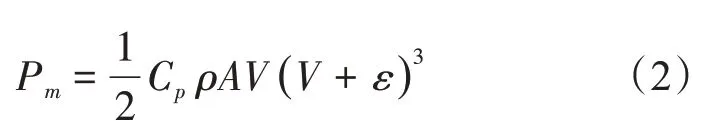
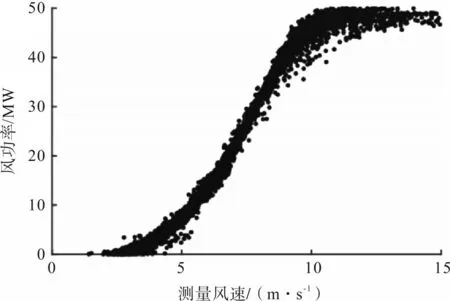
图1 实测风速与风电功率的关系

NWP 风速可以用来预测风力发电。在实际风电场中，NWP风速与风电功率的关系如图2所示。

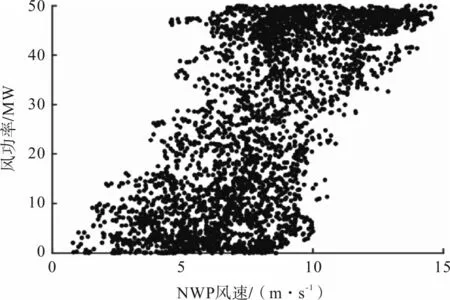
图2 NWP风速与风电功率的关系

从图1 和图2 可以看出，风速误差会导致预报误差。为了提高风力发电预测的精度，应运用误差修正方法，减小风速误差。因此，需要对NWP风速特征进行分析和提取。

1.2 湿地风速的特征分析

为了研究风速时间序列的统计特征，做出实测风速和NWP风速的直方图，如图3所示。由图可以看出，NWP风速的分布与实测风速的分布不同。

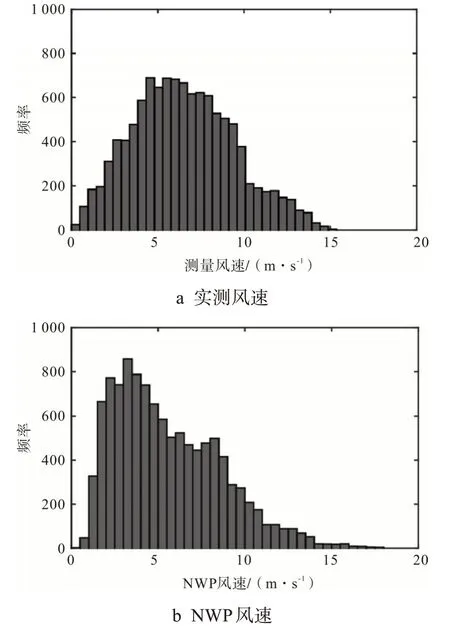
图3 实测风速和NWP风速

假设测量的风速是准确的，那么NWP 风速的误差为测量风速减去NWP 风速。在图4 中，黑线表示不同风速下NWP 风速误差的范围，点表示不同风速下NWP风速的中等误差，十字表示异常值。每一个风速值都有对应的风速误差分布。

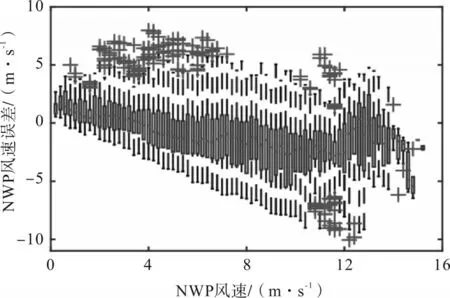
图4 风速误差

1.3 预测框架

通过以上分析，本文提出了一种基于双向门控递归单元神经网络GRUNN 的风速误差修正模型，用于风电机组的风速误差修正，以此来提高短期风电功率预测的精度。预测框架流程如图5所示。

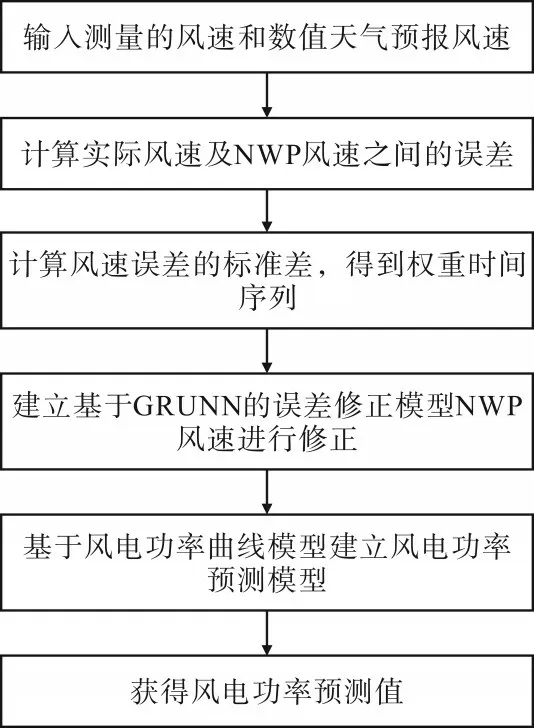
图5 预测框架流程

将NWP 风速误差的标准差设为权重时间序列。将权重时间序列分解为趋势项和细节项并输入到基于GRUNNs 的误差修正模型，对NWP 风速进行修正。将修正后的NWP风速应用于短期风电功率预测，可以有效地提高预测精度。

2 数值预报风速误差修正模型

本节提出了基于双向门控循环单元（GRU）-神经网络（NN）的数值预报风速误差修正模型，对数值预报风速误差进行了修正。

2.1 双向门控循环单元-神经网络

GRU 的体系结构如图6 所示。GRU 有两个门：复位门r调整新输入与先前存储器的合并；采用更新门z的控制方法来进行先前存储器的保存。

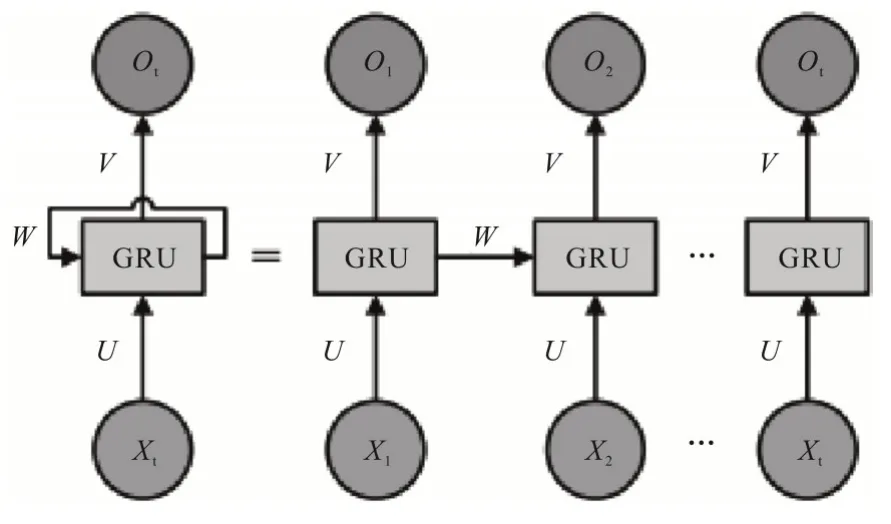
图6 基于GRU的RNN体系结构

式中，ot是一个神经细胞的函数；xt为输入；U、V和W分别是x、h和输出层的权重矩阵；f（i）是激活函数。

对于基于GRU的循环神经网络，如果按图8所示连接独立GRUNN，则该结构被开发为双向GRUNN。这种结构能够在两个方向上处理序列输入，包括前向和后向两个单独的隐藏层。每个隐藏层可以同时捕获过去（正向）和未来（反向）的数据信息。这种结构的双向性增加了模型的容量和灵活性。

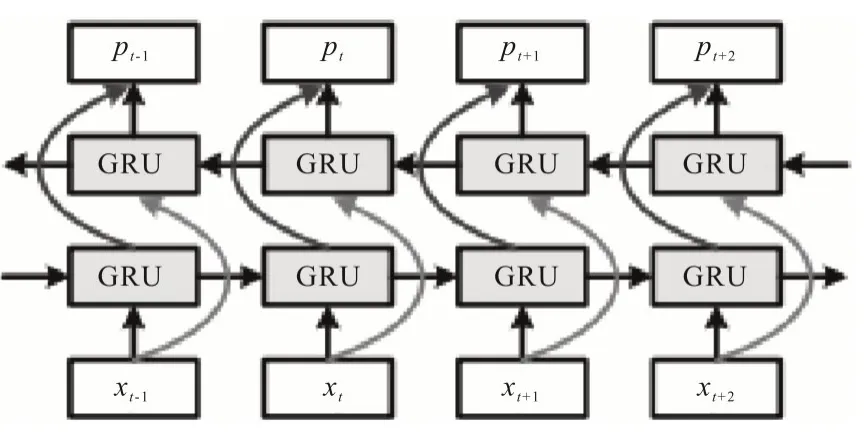
图7 双向GRU-NN结构

2.2 基于双向门控循环单元神经网络的误差修正模型

基于双向GRUNNs 的结构提出了风速误差修正模型，其体系结构如图8 所示。输入是时间序列数据，表示为X=［x1，x2，…，xn］，其中n是训练数据的长度。从训练数据的输入中提取局部特征。

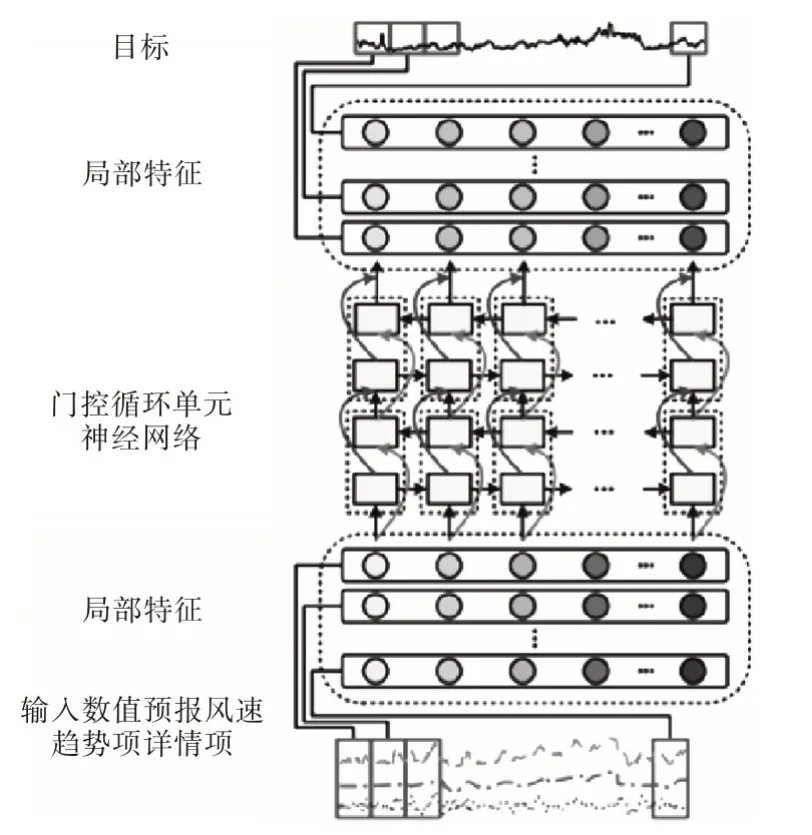
图8 风速误差修正模型体系结构

2.2.1 局部特征提取

每个输入被分成多个局部段，每段是长度为l 的原始信号的窗口，例如第j个局部窗口是从时间步长xj到xj+l-1的段。假设在局部特征提取之后，原始的输入被转换成一系列的局部特征，表达如下：

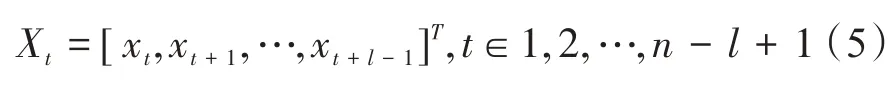
其中，Xt由t时刻窗口提取的l 个特征组成，与原始时间序列X相比，局部特征序列要短得多，并且比噪声原始输入传递更多的鉴别信息。

2.2.2 建模过程

为了充分利用风速时间序列的特点，提出了一种基于时间序列的风速预测方法，通过经验模态分解，将权重时间序列分解为趋势项和细节项。在误差校正模型中，X{x1，x2，···，xn}为输入矩阵，如式（6）所示。

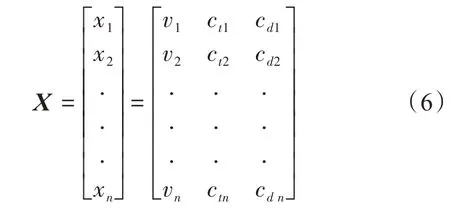
式中，v为NWP风速；ct为趋势项；cd为细节项。

利用式（6）得到局部特征矩阵：

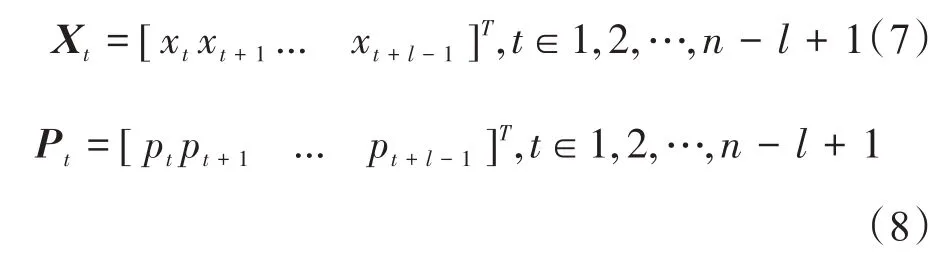
采用双向门控循环单元神经网络建立误差修正模型：

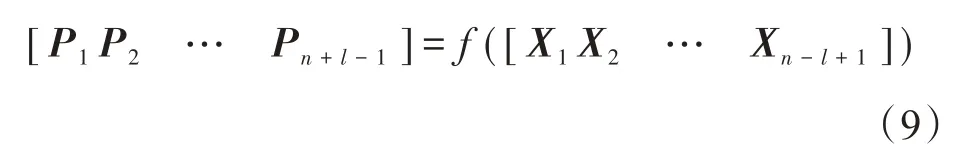
式中，f（·）是双向门控循环单元神经网络的训练函数。

式（9）可以写为

3 实验结果与分析

3.1 实验设计

使用一组从2016 年位于某省的一个风电场的实际数据中获得的，采样时间为15 min 的风速、风力和NWP风速数据。

3.2 评价标准

为了评价该模型的预测性能，以预测风力发电的均方根误差（RMSE）和平均绝对误差（MAE）为标准。在［0，1］范围内，RMSE和MAE数值较小意味着所提出的模型的性能更加优异。方程表示如下：

3.3 实验结果

利用风电场的实际数据进行实验，评价其性能，说明权重时间序列的生成过程，并对预测结果进行了说明。

3.3.1 重量时间序列

对于1 200 个样本点的数据集，通过从实测风速中减去NWP 风速，计算NWP 风速误差。在实测风速与NWP 风速误差之间，随着NWP 风速的增加，NWP 风速与实测风速的偏差发生变化，误差范围先增大，然后随着NWP 风速的增加而减小。通过分析发现，NWP风速为5 m/s～10 m/s的误差范围最大，其中提取NWP 风速误差标准差作为权重。根据NWP 风速时间序列，说明了NWP 风速不仅具有时间序列特征，而且NWP 风速误差也具有时间序列特征。例如，在第72个样本点的相邻点，NWP风速和NWP 风速误差大于其他点（第30 个和第95个样本点）。以其他时期为例，NWP 风速和NWP风速误差如图4 所示。这一特点要求考虑前进和后退时间系列信息。因此，利用NWP 风速误差的时间序列特性来修正NWP风速。

3.3.2 预测结果分析比较

NWP 风速的标准偏差误差被提取权重。重新整理NWP 风速误差时间序列的标准差，得到权重时间序列。通过经验模式分解，将权重时间序列分解为趋势项和细节项。趋势项和权重时间序列的细节项作为修正模型的输入，以历史实测风速作为输出，对模型进行训练，然后得到修正模型。由于风力与风速的立方关系，高风速段NWP 风速的不准确性比低风速段造成更多的误差。结果表明，当NWP 风速远高于实测风速时，该方法表现良好，仿真结果验证了其有效性。因此，该方法是非常有意义的。

采用修正后的NWP 风速，并结合风电功率曲线预测风电功率。将该方法预测的风电功率与神经网络模型和SVM 模型进行了比较，风电预测结果如图2 所示。预测结果的RMSE 和MAE 见表1和表2。从这些表中可以看出，采用修正的NWP模型，风电预测的精度有了很大的提高，所提出的模型优于所有基准模型。实验验证了该方法的有效性。

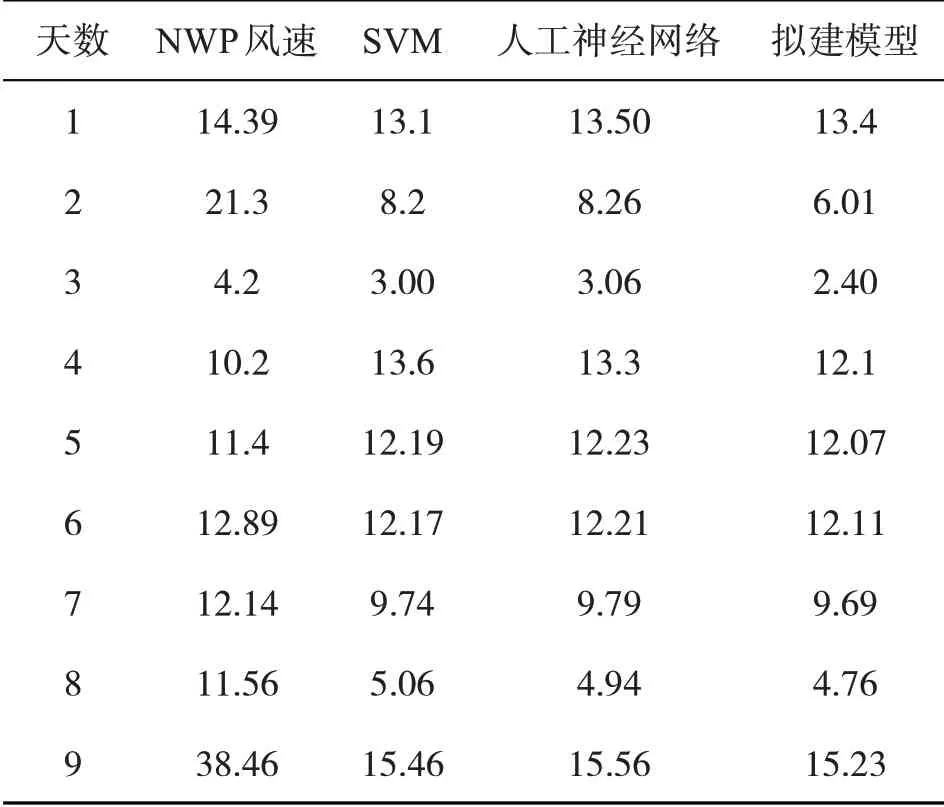
表1 预测风力发电的RMSE %

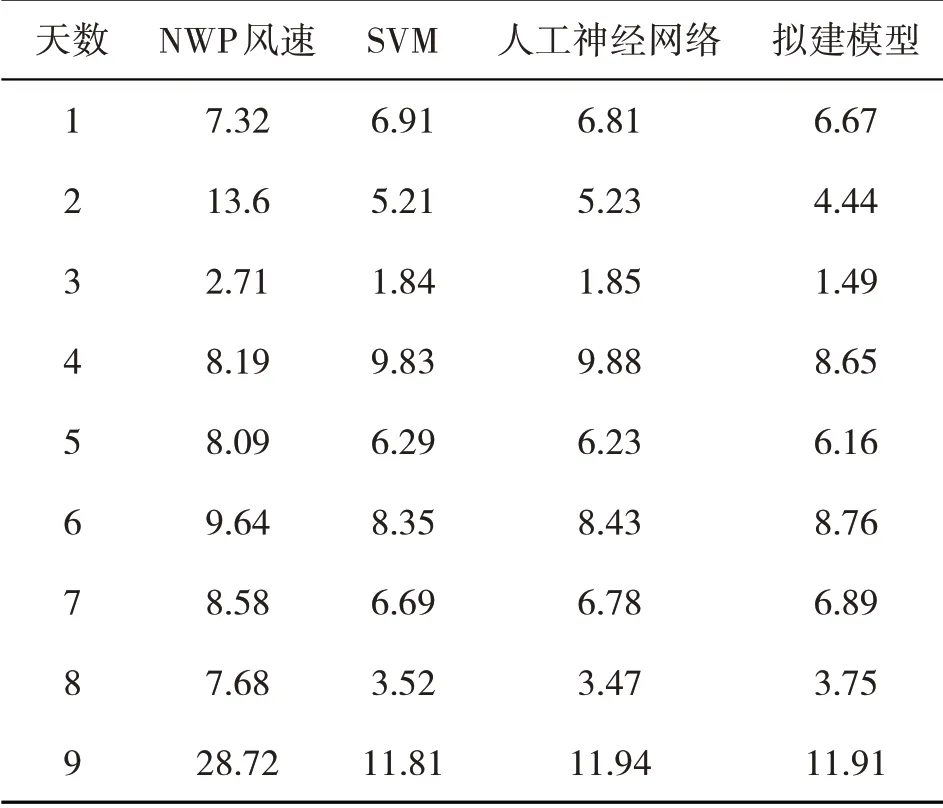
表2 预测风力发电的MAE %

4 总结

本文提出了一种基于门控递归神经网络的NWP 风速误差修正模型，该模型用于短期风电功率预测。首先，分析NWP 风速数据的特征并提取NWP 风速误差的标准差作为NWP 风速时间序列的权值。然后，提出了基于双向门控递归神经网络的误差修正模型来修正NWP 风速，使其更加贴近于风电场测风塔的风速数据。最后，将所提出的预测模型与基准模型进行了有效性比较。实验结果表明，该模型具有较好的短期风电功率预测能力。由于中长期数值天气预报数据同时具有统计特性和时间序列特性，因此该方法也可用于中长期风电功率预测。