《梯形的面积》项目式学习教学设计

王学农

教师在课堂上为学生创设充分的自主探究的时间和机会，引导学生独立思考和积极尝试，在操作中比较，在比较中发现，在发现中总结，从而完成教学目标。

【学习内容】北师大版小学数学五年级上册P59～60

【教材解读】

这部分内容的教与学，是在学生经历了平行四边形的面积和三角形的面积这两个探索活动之后进行的。在它的后面还有组合图形的面积和不规则图形面积的学习。

教材内容呈现的几个环节与前面两个探索活动平行四边形的面积和三角形的面积相似。考虑到梯形的面积涉及到上底、下底及高的复杂关系，加上学生对用两个完全一样的三角形拼成一个平行四边形和割补法有了一定的经验和较深的体会。所以，教材在呈现情境图“堤坝横截面的面积”之后，直接提出了“把梯形转化成学过的图形，并比较转化前后图形的面积”这一关键性的问题，把学生引向把一个新的图形转化为学过的几何图形来推导，直奔独立思考、动手操作的探究活动。

【设计理念】

新课程标准明确提出：学生的数学学习应当是一个生动活泼的、主动的和富有个性的过程。认真思考、动手操作、自主探究、合作交流，都是数学学习的重要方式。学生应当有足够的时间和空间经历观察、实验、推理、验证等活动过程。

教师在课堂上出示探究的情境图之后，为学生创设充分的自主探究的时间与机会，引导激励学生在已有知识经验的基础上独立思考和大胆尝试。在操作中去比较，在比较中去发现，在发现中去总结，从而真正领悟并掌握怎样计算梯形的面积，发展学生推理归纳和解决问题的能力。

【学习目标】

1.经历梯形面积的探索活动过程，体验割补法在探究中的应用。

2.掌握梯形面积的计算方法，并能用梯形面积的计算方法解决生活中相关的实际问题。

【学习重点】

经历探索梯形面积计算方法的过程，理解梯形面积的计算公式，并能灵活运用。

【学习难点】用拼、割补等不同的方法去推导梯形面积的计算公式。

【教学过程】

一、设置情境，提出问题

1.情境创设：课件展出大堤的横截面示意图（见课本P59图1）。

2.提出问题：如何求出图中梯形的面积？

二、提供材料，合作探究

1.研究建议。（1）先想一想，能把它转化成已学过的什么几何图形，再按照“转化—找联系—推导公式”的思路来研究；（2）把你的推导方法跟小组成员进行分享，一起来验证。

（设计意图：研究建议充分体现教师合作者和指导者的课堂角色。学生经过独立思考，对问题有了自己的认识，再进行合作交流。）

2.合作探究。探究材料：每个小组4个完全一样的梯形（有的小组是等腰梯形，有的小组是直角梯形，有的是一般梯形）、剪刀、学习单。

3.汇报展示。

（1）展示“拼”的方法。

方法一：用两个形状相同、大小一样的普通梯形拼成一个平行四边形。（见教材P59图2）拼成的平行四边形的面积等于原来一个梯形的面积的2倍。平行四边形面积等于底乘高，平行四边形的底等于梯形的上底与下底的和，平行四边形的高等于梯形的高，所以，梯形的面积等于梯形的上底与下底的和乘高除以2。

方法二：用两个形状相同、大小一样的直角梯形来拼成一个长方形。同样可以得出梯形的面积等于梯形的上底与下底的和乘高除以2。

（2）展示“割补”的方法。

方法三：把一个梯形沿中位线分，分成两个梯形，再拼成一个平行四边形（直角梯形拼成的是一个长方形）（见教材P59图2）。梯形的面积等于拼成的平行四边形的面积。平行四边形的面积等于底乘高，平行四边形的底等于梯形的上底与下底的和，平行四边形的高等于梯形的高的一半，所以，梯形的面积等于梯形的上底与下底的和乘高除以2。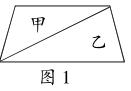

方法四：把梯形沿其中一条对角线分成兩个三角形甲和乙（如图1）三角形甲的面积等于梯形的上底乘高除以2，三角形乙的面积等于梯形的下底乘高除以2。同样可以得出，梯形的面积等于梯形的上底与下底的和乘高除以2。（设计意图：只要给学生明确的探究主题和充分的探究材料、时间、空间，学生一定会呈出现多种探究的成果。展示探究成果，汇报探索方法，展现思考过程，交流收获体会的环节，能有效锻炼学生有条理地表述小组的探究过程，倾听和理解其他学生的探究思路，还能有效激发学生的学习兴趣，获得成功愉悦的学习体验。）

三、梳理归纳，加深认知

1.播放微课视频：探究《梯形面积》公式的4种方法。

2.强调“转化”的方法和得出的结论：梯形的面积=（上底+下底）伊高衣2，用字母表示为S=（a+b）伊h衣2。

四、练习巩固，拓展应用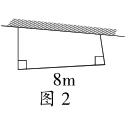

1.求出大坝横截面的面积（见课始情境图）。

2.学校篮球场罚球区是一个梯形，上底3.6米，下底6.5米，高5.8米，求篮球场罚球区的面积。

3.王大爷靠墙用篱笆围了一块菜地，已知篱笆全长36米，你能算出菜地的面积吗？（如图2）

（设计意图：练习内容的设计，充满了生活气息，充分体现了数学来自于生活，又服务于生活。这样的练习，在检查学生是否真正理解和掌握梯形面积的同时，让学生充分体会到学数学的应用价值。）