400 km/h高速铁路常用跨度混凝土简支梁竖向基频研究

李克冰 班新林 郭建勋 谢海清

(1.中国铁道科学研究院集团有限公司， 北京 100081；2.中铁二院工程集团有限责任公司， 成都 610031)

高速铁路桥梁结构需要保证列车高速运行的安全性和稳定性，需具有足够的刚度，为避免较大的车桥共振响应的出现，国内外高铁桥梁相关规范均对竖向自振频率进行了严格限制。

国际铁路联盟(UIC)早期组织相关研究机构针对各种运营列车，进行了大量的车桥动力计算分析，以确定不同跨度简支梁竖向基频限值。式(1)、式(2)分别给出了梁体竖向基频的上、下限，基频下限用于保证高速列车通过时桥梁不出现共振或者较大振动，基频上限用于防止桥上轨道不平顺引起的动力响应过大。

n0=94.76L-0.748

(1)

(2)

此后，欧盟在新标准[1]中进一步明确了高速铁路桥梁设计中动力分析流程和检算内容，并提出了不需进行动力分析的激振波长v/(3.6n0)限值。

日本新干线桥梁设计标准采用近似运营列车的H荷载作为活载图式和极限状态设计方法，其对桥梁刚度和基频的限制主要在于控制由连续移动荷载的速度效应引起的冲击。1992年，日本在《铁道构造物设计标准和解释—混凝土结构》中，基于式(3)速度参量α制定了铁路混凝土桥动力系数，并指出当速度参量α>0.33时，将引起较大冲击。

(3)

式中：v——列车速度(km/h)；

N——构件的频率(Hz)；

Lb——构件的跨长(m)。

为适应新干线高速化的发展，日本于2004年编制了新版《铁道构造物设计标准和解释—混凝土结构》，于2006年制定《铁道构造物设计标准和解释—变形限制》，并提出了桥梁动力系数查照图表，同时在进行大量的动力分析和试验的基础上，引入了新的设计动力系数计算方法：

i=(1+ia)×(1+ic)-1

(4)

式中：ia——列车荷载速度效应引起的动力系数，与速度参量α、列车长度、桥梁跨度相关，通过查照图表取值；

ic——车辆振动引起的动力系数，与桥梁跨度相关。

我国规范[2]中250～350 km/h高速铁路桥梁的竖向自振频率下限值制订时，考虑到桥梁设计中采用的ZK活载图式是基于国际铁路联盟UIC活载图式制定的，参考了UIC规范的规定，并总结提出了不同设计速度条件下40 m以下混凝土及预应力混凝土双线简支梁不需要进行车桥耦合动力分析的竖向基频限值。

更高速度的高速铁路是世界铁路研究发展的趋势，意大利于2015年研制出设计400 km/h的高速列车，并开展了400 km/h的相关性能试验，我国中铁二院工程集团有限责任公司2015年6月签下400 km/h的俄罗斯莫斯科-喀山高速铁路设计项目，完成了莫喀高速铁路项目桥涵统一跨构通用图设计[3]。同时，美国、英国、俄罗斯等国家均提出建设400 km/h高速铁路的需求。新建成渝中线高速铁路建设标志着我国更高速度高速铁路的工程实现。

本文采用移动荷载列分析模型，通过计算分析不同运营列车通过不同基频的32 m、40 m双线混凝土简支箱梁时的梁体动力响应，以运营活载的桥梁动力效应不大于设计活载的桥梁动力效应为标准，确定了400 km/h高速铁路常用跨度简支梁的基频限值。

1 分析模型

1.1 移动荷载列分析模型

对列车作用下的桥梁动力响应研究，移动荷载列分析模型简便易行，可以很好地反映列车对桥梁的周期性激励规律。Fryba[4]将列车简化为移动荷载模型，使用移动力作用于简支梁的解析指导了国际铁路联盟相应标准的制定。杨永斌[5]等采用动态凝聚法研究桥梁的动力系数，同时与移动荷载列计算结果进行对比，两者吻合度较好。沈锐利[6]在研究中比较了移动荷载列模型与车桥耦合分析模型作用下简支梁的动力响应，结果表明两者反映的振动响应特征基本一致。

本文采用移动荷载列分析模型。选择不同基频的桥梁模型，通过计算列车以不同速度通过时桥梁的动力响应，在综合分析桥梁动力响应与列车类型、运行速度、桥梁基频的关系基础上，确定梁体基频合理限值。

移动荷载作用下桥梁的竖向振动响应与桥梁跨度、自振频率、列车速度、轴重排列等有关。移动荷载列模型中将桥上的列车按照列车轮重、轮距简化为一系列具有一定间距的移动集中力荷载列，如图1所示。图中，lw为轴距，lc为定距，d为车长，L为桥梁跨度。荷载在桥上以速度V匀速通过。采用有限元方法建立桥梁模型，假设简支梁为等截面(EI为常数)，桥梁质量及阻尼特性沿桥跨方向均匀分布。计算分析中32 m、40 m简支梁的截面尺寸如图2所示。二期恒载分别取为180 kN/m、160 kN/m，桥梁结构阻尼采用Rayleigh阻尼，阻尼比取1.2%，梁体的计算频率为 1～8 Hz。

图1 移动荷载列示意图

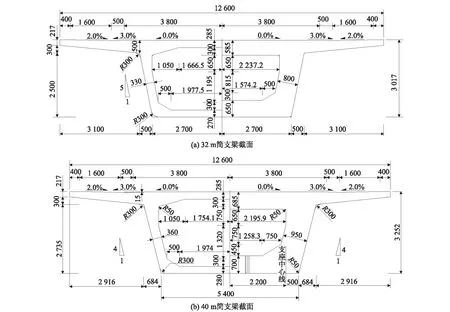
图2 不同简支梁横截面图(mm)

计算列车采用CRH380A、CRH380B和中国标准动车组，编组形式为8节编组。CRH380A列车最大轴重15 t，头车长26.5 m，中间车长25 m；CRH380B列车最大轴重17 t，头车长25.85 m，中间车长24.825 m；标准动车组列车最大轴重17 t，头车长27.065 m，中间车长25.65 m。最大计算速度为510 km/h。

1.2 评判标准

列车作用下，无砟桥面在20 Hz及以下的竖向振动加速度不应大于5.0 m/s2(半峰值)。

我国高速铁路设计荷载为ZK荷载，设计动力系数为1+μ。为保证桥梁不产生共振以及实际运营荷载产生的内力不超过设计值，桥梁的实际运营动力系数不应大于相应的容许动力系数，容许动力系数计算公式如下：

(5)

式中：Lφ——加载长度(m)。

计算不同跨度的混凝土简支箱梁在ZK活载和移动荷载作用下的静力效应，得到不同列车对应不同跨度简支箱梁的容许动力系数，如表1所示。

表1 动车组容许弯矩动力系数统计表

2 简支梁动力响应分析

2.1 与车桥耦合动力分析模型的对比

相对于复杂的车桥耦合动力分析模型，移动荷载列模型忽略了列车桥梁之间的相互作用。本文首先对这两种分析模型进行了比较分析。以我国高速铁路无砟轨道不平顺谱生成的样本(截止波长120 m)为激励源，采用车桥耦合动力模型计算了跨度32 m简支箱梁在CRH2型列车运营条件下的动力响应，并与移动荷载列模型的计算结果进行对比，如图3 所示。从图3中可以看出，在各种计算工况下车-桥耦合动力分析模型和移动荷载列模型冲击系数计算结果吻合良好。对于高速铁路简支梁，由于梁体截面较大，且运营列车轴重较轻，使得梁体质量远大于车体质量，车辆惯性力对桥梁振动的影响较小，移动荷载列模型能够很好的反映列车荷载作用下桥梁的动力响应规律，采用移动荷载列模型研究确定梁体基频限值是适宜的。

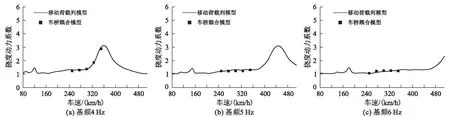
图3 不同分析模型下32 m简支梁动力响应对比图

2.2 不同跨度简支梁的动力响应特征

基于移动荷载列分析模型，对不同基频的32 m、40 m简支梁在不同列车作用下的动力响应进行计算分析。

国内外既有理论与试验研究[7-8]均表明，对于不同跨度的简支梁，高速列车速度效应引起的激振规律是一致的，主要与运行速度和车辆长度有关(见式(6))。当列车激振频率为结构自振频率的1、1/2和1/3时，可能发生共振或较大振动。

fv=V/(3.6d)

(6)

式中：fv——列车速度效应引起的激振频率(Hz)。

当列车荷载通过简支梁的时间满足一定条件时，移动荷载所引起的自由振动将相互抵消，发生消振现象。既有研究[9-10]表明，当车辆长度d与桥梁跨度L之比为一定关系时，会同时满足共振及消振响应的发生条件，这时消振起主要作用，即发生共振消失现象。当梁跨与车长比L/d=k+0.5(k=1，2，3…)时，梁体不存在1阶共振点，车桥动力响应最小。

32 m与40 m跨度不同列车作用下的动力系数图如图4～图7所示。从图4～图7中可以看出：

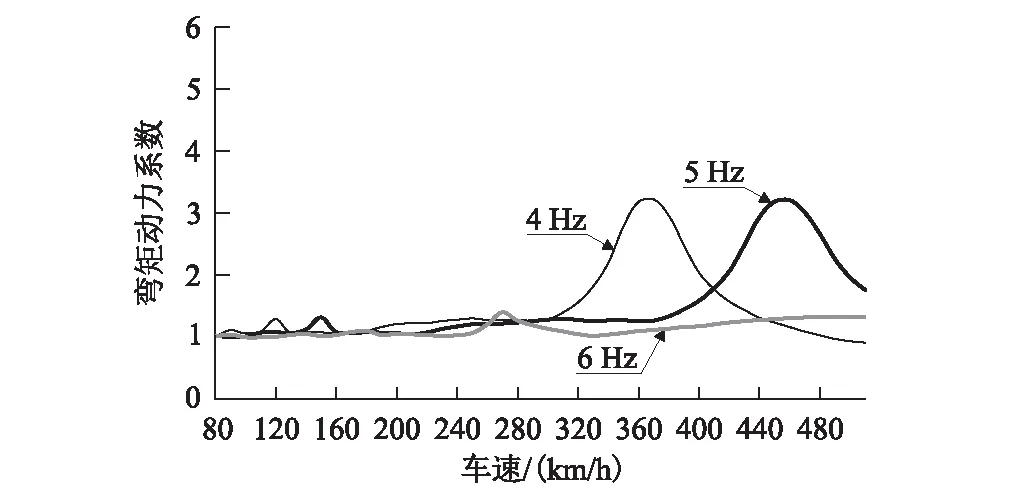
图4 标准动车组作用下不同基频的32 m简支梁的弯矩动力系数图

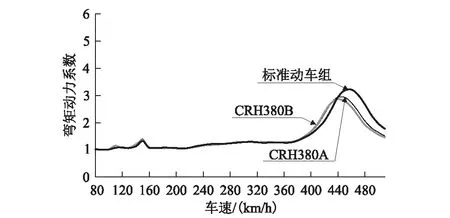
图5 不同列车作用下32 m简支梁(5 Hz)的动力系数图

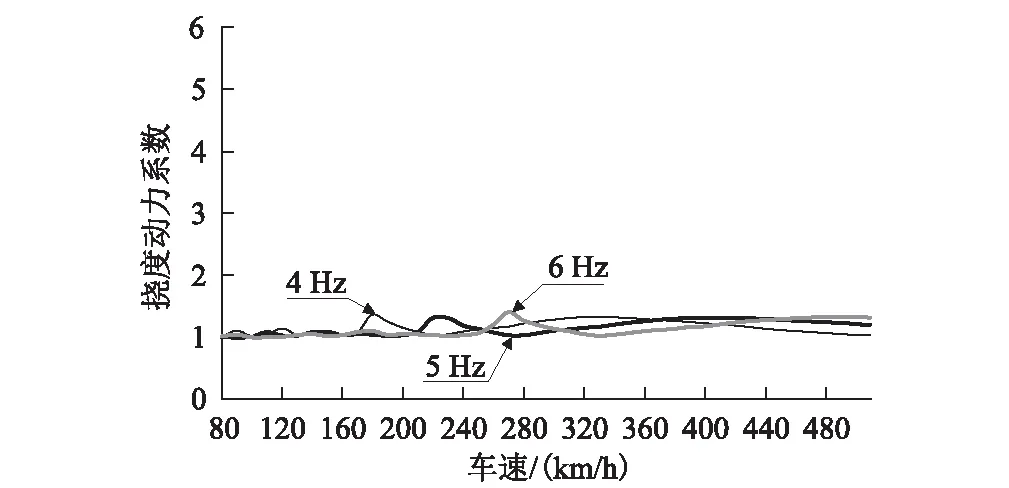
图6 标准动车组作用下不同基频的40 m简支梁的动力系数图

图7 不同列车作用下40 m简支梁(5 Hz)的动力系数图

(1)相同列车作用下，随着简支梁基频的增大，动力系数最大值对应的车速变大。基频的变化对于动力系数最大值的变化影响很小。

(2)基频为5 Hz的32 m简支梁在CRH380A、CRH380B和标准动车组作用下的共振速度分别为450 km/h、446 km/h和462 km/h。相同基频条件下，列车的车长越大，动力系数的最大值越大，对应的共振车车速也越大。

(3)相同列车作用下，40 m简支梁动力系数峰值明显小于32 m简支梁。根据前述研究成果，对于车长25 m左右的CRH系列高速列车，当梁体跨度为37.5 m时不存在1阶共振点。40 m简支梁靠近消振跨度，梁体动力响应明显减小。

(4)对于32 m简支梁，提高梁体的基频可以有效提高共振速度，显著降低在运行速度及以下速度行驶时的动力响应。对40 m简支梁，提高基频对于梁体动力响应峰值的降低无明显效果。

3 基频限值研究

32 m与40 m跨度相同线质量的简支梁梁体在不同运营速度的列车作用下的最大动力响应随竖向基频的变化曲线如图8～图10所示。从图8～图10可以看出：

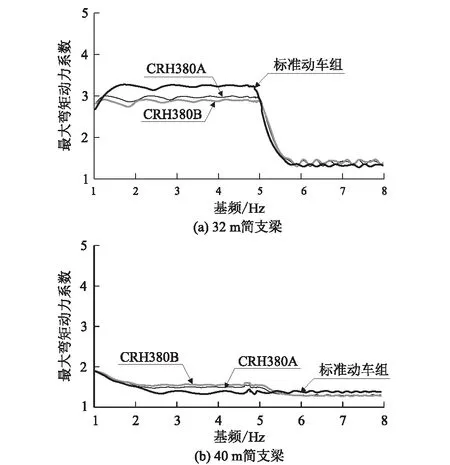
图8 440 km/h列车作用下简支梁最大动力系数图

图9 不同速度标准动车组作用下简支梁最大动力系数图

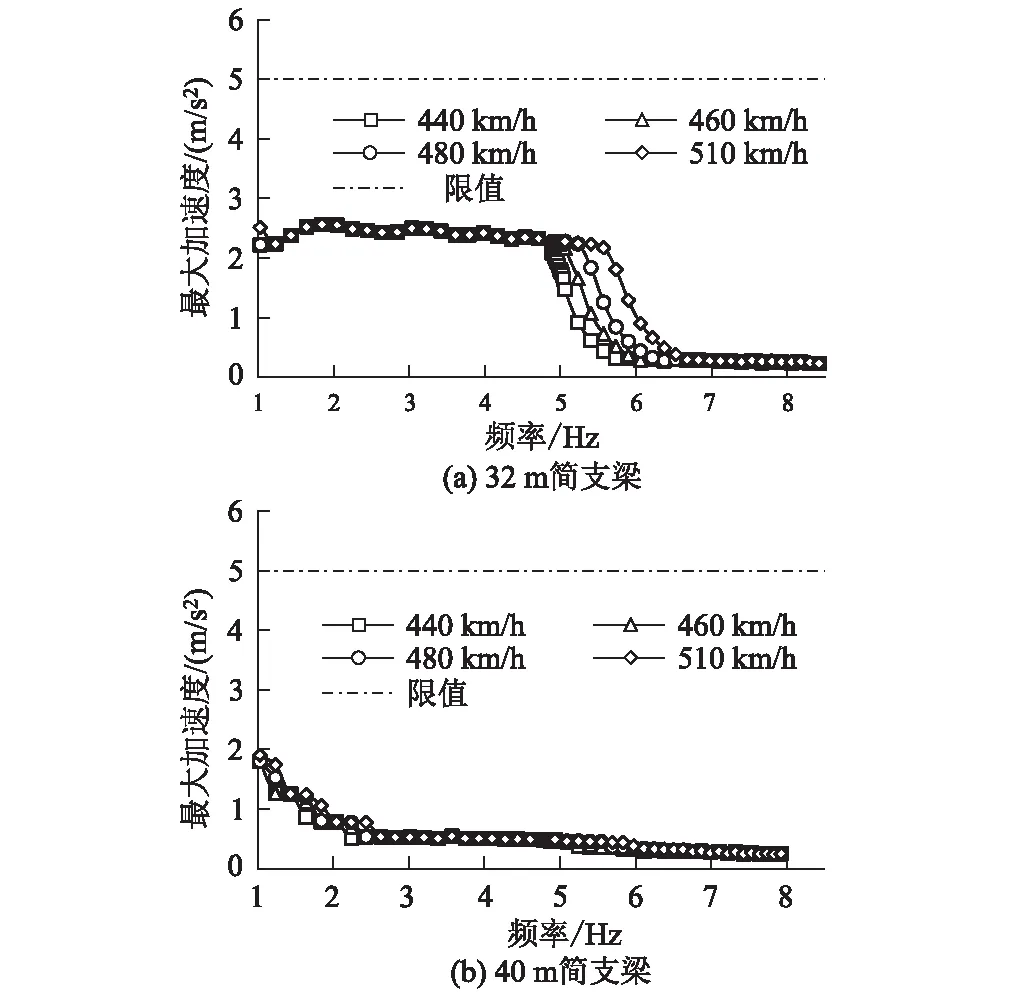
图10 不同速度标准动车作用下简支梁最大梁体竖向加速度图

(1)梁体最大动力响应随着梁体频率的增加而下降的趋势呈台阶状，32 m简支梁的台阶变化比40 m简支梁明显。基频较小时，共振车速小于计算车速，此时基频变化对动力响应最大值的影响较小；当桥梁基频对应的共振速度接近计算车速时，基频增大能有效降低动力响应峰值；桥梁基频较大时，计算速度远小于共振速度，基频对动力响应的峰值影响也很小。这对于我们取梁体基频限值是可信、可行的一种方法。

(2)除了CRH380A以外，列车作用下较小基频的32 m简支梁最大弯矩动力系数大于容许动力系数；40 m简支梁在不同列车作用下的最大弯矩动力系数都不超过评判限值，40 m简支梁动力系数明显小于32 m简支梁。

(3)梁体最大竖向加速度与动力系数的变化规律一致。在计算采用的质量条件下，32 m与40 m简支梁的梁体竖向加速度都不超过规范限值。

(4)随着计算速度的增大，梁体最大动力响应的曲线向基频更大的方向移动。设计速度提高，为避免共振现象的出现，基频也需提高。

根据1.2节的评判标准，设计400 km/h的高速铁路32 m混凝土双线简支箱梁分别按1.1倍、1.15倍、1.2倍、1.25倍检算速度确定的梁体基频下限值如表2所示。考虑到新建400 km/h高速铁路运营速度进一步提升的可能性不大，建议32 m混凝土简支梁按440 km/h计算结果确定基频限值，即5.1 Hz(160/L)。

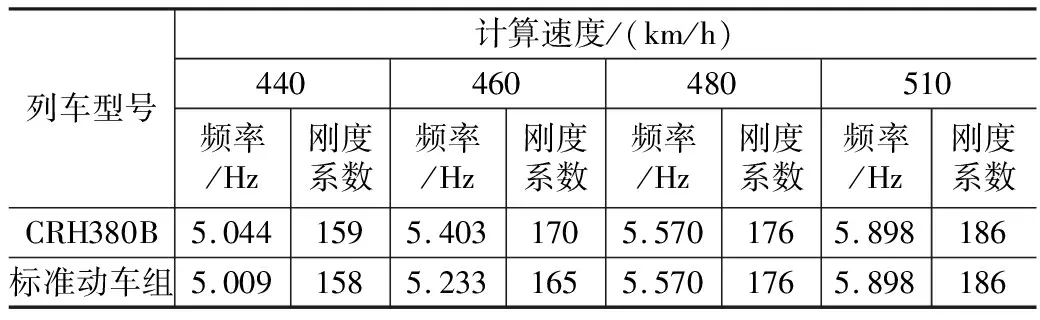
表2 不同速度下32 m简支梁梁体基频与梁体刚度系数下限值表

在计算基频与速度范围内，40 m简支梁的最大动力系数和最大梁体加速度均满足评判标准，因此，对于400 km/h高速铁路，40 m简支梁的基频满足规范规定的下限值(即23.58L-0.592)即可。

4 结论

本文采用移动荷载列方法，对400 km/h高速铁路常用跨度混凝土简支梁的竖向基频进行了研究，得出主要结论如下：

(1)移动荷载列模型和车-桥耦合动力分析模型的动力系数计算结果吻合良好。移动荷载列模型能够很好的反映列车荷载作用下桥梁的动力响应规律，采用移动荷载列模型研究确定梁体基频限值是适宜的。

(2)通过调整简支梁的基频，使其避开列车对梁体的激振频率，从而避免梁体共振的发生，可显著降低梁体的动力响应。

(3)提高基频对于降低40 m简支梁的动力响应无明显效果。对于车长25 m的CRH系列高速动车组，40 m简支梁接近消振跨度(37.5 m)，梁体动力系数与竖向加速度明显小32 m简支梁。40 m简支梁对400 km/h高速铁路适应性更好。

(4)400 km/h高速铁路32 m混凝土双线简支梁不需进行动力检算的基频限值建议取5.1 Hz(160/L)，40 m混凝土简支梁基频按规范规定的基频下限值取即可。