基于广义Snell 定律的声超表面折射

楚琦琦胡 宇林 玮

(南京航空航天大学应用物理系，江苏南京 211100)

材料是人类社会存在的重要物质基础，与社会生产力的发展息息相关。但传统材料受其本身物理、化学性质的限制，无法满足人们对其在某些场合的特殊需求。而超材料的出现冲破了传统材料固有性质的束缚，解决了这一难题[1]。超材料[2]是一类不同于传统材料、由亚波长人工微结构单元组成、具有特殊功能的材料，人们可以通过改变微结构的构型实现所需要的不同功能[3]。其中，属于超材料的超表面[4-6]由于体积小，因此由其制作出相应的器件具有尺寸较小、结构简单、低损耗等优点，得到了越来越广泛的应用[7-9]。

2013 年，李勇等人[10]设计了类似于叉指换能器形状折叠空间结构声超表面，这是第1 次在亚波长尺度下利用声超表面实现对声波相位的有效调控，该结构各单元相位覆盖范围为0～2π 且规律变化，很好地模拟了声学异常反射现象；2015 年Tian 等人[11]通过设计梯度单元声超表面也实现了声波的异常折射、贝塞尔波束、声聚焦等一系列奇异现象；南京大学朱一凡等人[12]设计了一种梯度型超表面，实现了宽频带范围内声波的异常反射现象。基于前辈们的工作，可总结出由于声波在声超表面单元内传播路径的长短不同实现对其相位的调制，从而实现对声波灵活操控的经验。因此，文章利用一种深浅窄阱型声超表面，较好地仿真了声波的异常折射现象。

1 理论基础

已知作为几何光学的基本实验定律之一的折射定律满足关系式:

式中:n1、n2分别为分界面两侧介质的折射率，θi为入射波相应的入射角、θt为折射波相应的折射角，如图1(a)所示。以上也被称为传统Snell 定律。

由于光波、声波具有相似性，即满足相似的波动方程，具有相同的波矢等波参数，故声波也遵循上述Snell 定律。但当在两介质分界面上引入相位突变时，入射波、折射波不再满足普通的折射定律，如图1(b)所示。

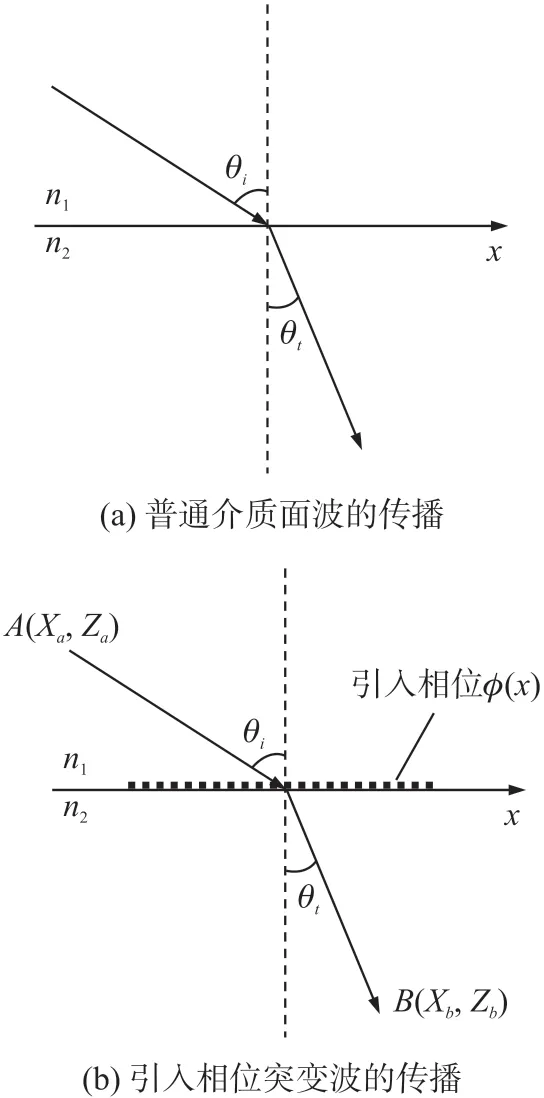
图1 两种折射定律示意图

声波从A(Xa，Za)点出发，经附带相位φ(x)的声超表面传播到B(Xb，Zb)点。由费马原理，即光沿实际光程取极小值的路径传播，将其应用在上述声波传播的路径中，即声波沿声程取极小值的路径传播，换一种说法，声波沿相位取极小值的路径传播。设分界点坐标为(X，0)，声波由A点传播到B点的相位变化为:

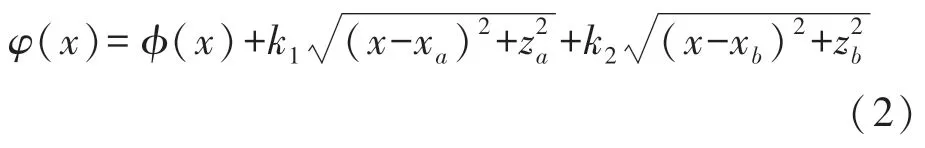
式中:k1、k2分别是入射介质面、折射介质面的波矢，且有k＝2π/λ。

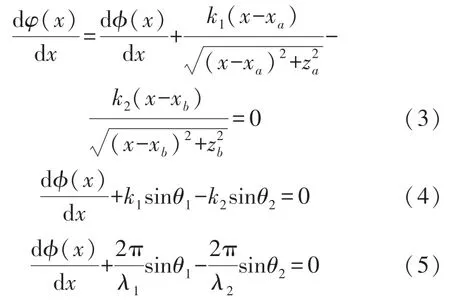
式中:λ1、λ2为入射波、折射波的波长。上式可化简为:

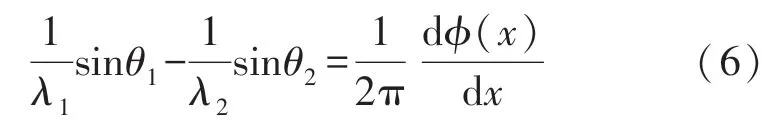
此为广义Snell 折射定律的表达式。由式(5)可看出，当＝0 时，表达式满足普通广义Snell定律；当≠0 时，我们可以通过适当设计的值，给定不同的入射角，获得想要的不同折射角，达到任意控制声波的目的。

2 构建模型

2.1 设计结构

为实现对声波的相位调制，利用一种窄阱结构，基于声波在声超表面各单元传播时路径长短不同而使得相位不同的原理，在相邻高矮井之间实现0 到2π 范围的相位调制，部分结构如图2 所示。

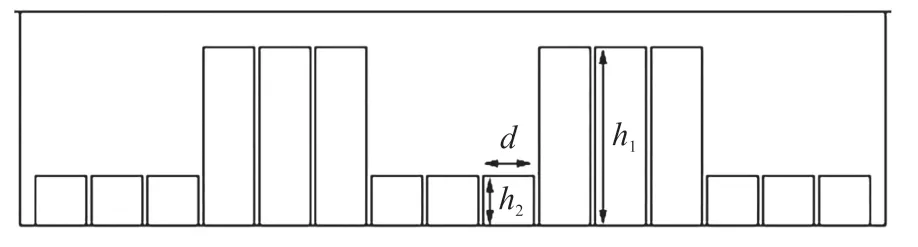
图2 声超表面结构图

此结构由一排周期性的深浅凹槽构成，且每组深浅凹槽有3 个窄阱单元，其尺度设计在亚波长级别，设计参数如下:h1＝35 cm，h2＝9.75 cm，d＝10 cm，故Δh＝25.25 cm。窄阱内部填充介质1 材料铅，窄阱外部以及上表面填充介质2 材料铁，二者相关参数如表1 所示。

表1 介质材料参数表

声波在深浅凹槽中传播至分界面处的相位差为Δφ＝(k1-k2)*Δh，由公式k＝2π/λ，λ＝c/f，其中f为入射声波的频率，在此我们设定8 500 Hz，可求得声波通过相邻凹槽后的相位差为π，则将结构排列成偶数周期型凹槽结构，可实现0 到2π 范围的相位变化。

2.2 模拟仿真

研究方法采用有限元分析法，构建一半径为720 cm 的圆域，将其一分为二，并将上述声超表面结构导入到二者分界面处，然后在上下表面分别填充不同的介质，结构模型如图3 所示。

在下表面我们给定y轴方向平面波辐射的背景压力场，使得声波以0°入射，且声超表面结构左右两侧的分界面处设置硬声壁，使入射波不透过，从而明显地看出声超表面对入射波产生的影响。

图3 构建几何模型图

2.3 结果分析

由上述理论，当声波以0°入射，声波通过相邻高矮窄井的相位差为π，而一组窄井宽度Δx为30 cm，将该数据代入广义Snell 折射定律表达式可得折射角约为53°，仿真结果如图4 所示。

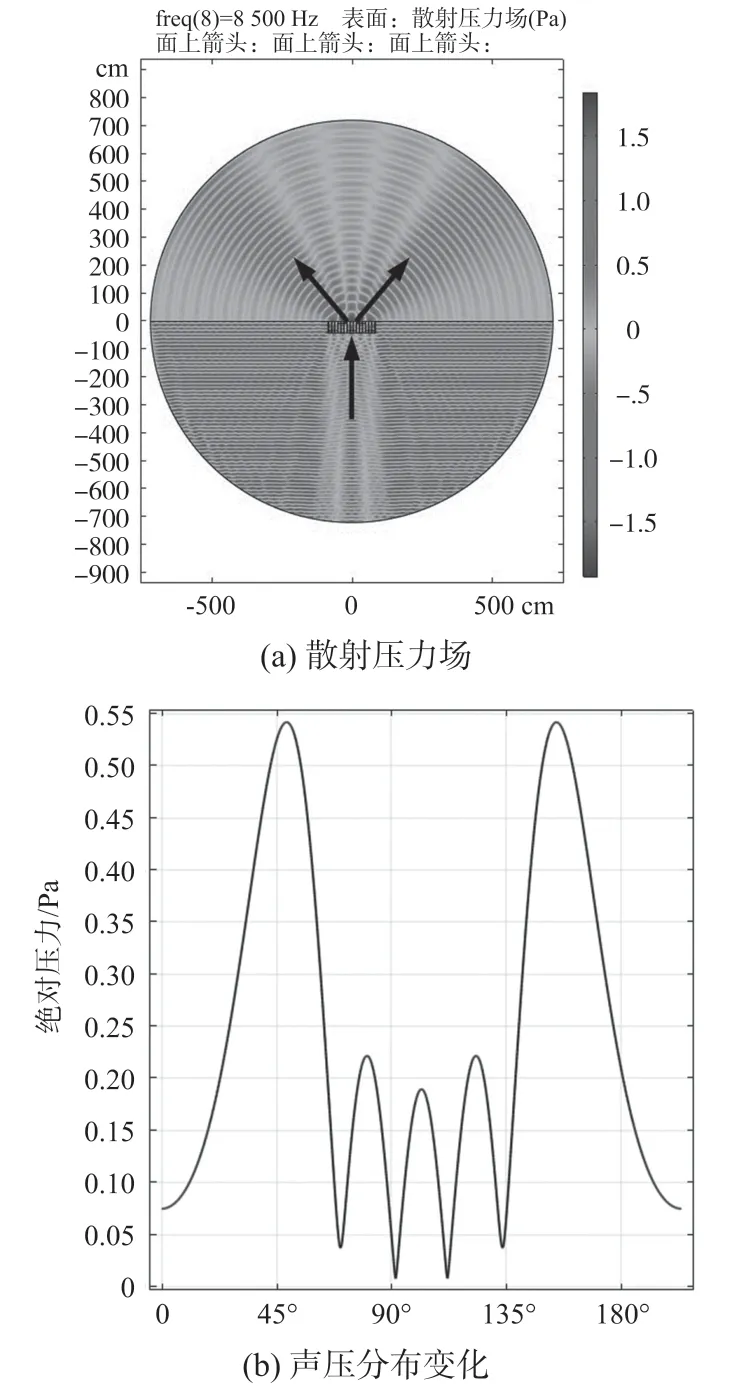
图4 仿真结果图

由图4(a)、图4(b)可以看出，实际出射声波角度在误差范围内符合理论计算角度，且由于声波通过相邻高矮窄阱后的相位差为π，使得声波出射有2 个方向，从而有对称的两束出射波，且声压幅值分别在约为48°、137°处表现明显，较好地验证了广义Snell 折射定律。

将上述声超表面结构进行周期性地拓展，各单元尺度大小不变，使其铺满两介质分界面，如图5所示。

图5 拓展周期结构模型图

同样在下表面给定平面波辐射的背景压力场，且压力幅值设为1，计算后散射压力场如图6 所示。

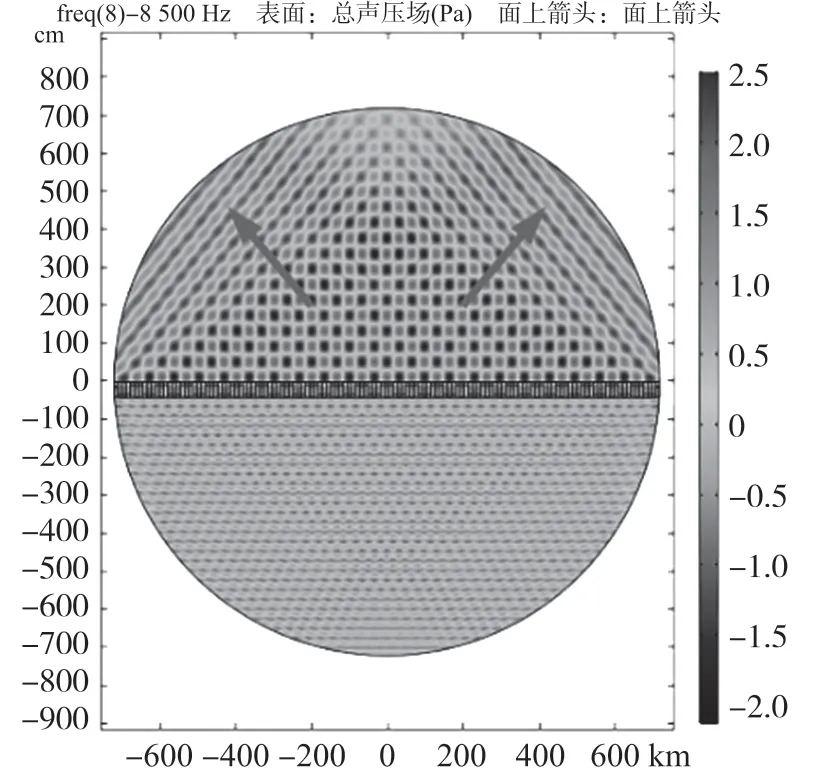
图6 拓展周期结构散射压力场

由图6 可知，透过声超表面的声波依然遵循广义Snell 定律，折射角符合理论计算，但与部分周期结构透过声波不同的是，往左右方向折射的声波交叠部分较大，若过滤一个方向的声波，折射现象就显得较为明显了。

3 总结

文中利用的声超表面结构很好地验证了广义Snell 折射定律，实现了声波的异常折射。通过改变结构的参数，即窄阱的高矮比例，得到任意的波方向。此结构在设置好匹配材料的前提下，不需考虑透射率的大小，但不足之处在于频带范围较窄，后期需进一步改善，实现宽频带折射。人们可以以上述结构为启发，进一步地实现声聚焦功能。