基于PAU-LSSVM 模型融合多特征变量的电力负荷预测

李雪冬黄 莹胡 勇李怀强高齐利

(1.北京中恒博瑞数字电力科技有限公司，北京 100085；2.国家电网公司西北分部，陕西西安 710004)

电力系统负荷预测对电力系统给的运行、生产和规划起着重要的作用，同时也为电网稳定经济运行奠定了基础[1]。Hobbs 的报告[2]曾经指出:将电力负荷预测的平均绝对百分误差降低1.5%，每年可提高收益760 万USD。精准的负荷预测有利于节能调度以及精细化管理，有利于电网监测的自动化和智能化水平的提升[3]。因此，实现负荷的精准预测具有重要的意义。

近年来，为了实现负荷的精准预测，众多学者对电力负荷预测的方法进行了积极地研究[4-6]。传统的负荷预测模型有:时间序列分析模型、回归模型和自回归移动平均模型，但这些方法对非线性关系数据的预测能力有限。随着人工智能技术的发展，负荷预测进入了崭新的阶段，陈艳平等[7]利用经验模式分解EEMD-样本熵将原始电力负荷序列分解，使用Elman 神经网络对各子序列分别进行预测。喻圣等[8]基于模糊神经网络建立了负荷预测模型。李冬辉等[9]提出了一种将多种群的果蝇优化算法和广义回归神经网相结合的电力负荷预测模型。

随着电网负荷数据呈几何增长，一般的人工智能算法将不能满足处理海量数据的要求。因此，王保义[10-11]、吴润泽等[12]将Hadoop、Spark 大数据框架与最小二乘支持向量机(least squares support vector machine，LSSVM)、极限学习机等算法相结合进行负荷预测。随着深度学习的发展，王增平[13]、张旭东[14]、朱俊丞等[15]应用不同的深度学习网络对电力负荷进行预测，这些深度学习模型大大提高了负荷预测精度[16-17]，其中，基于长短时记忆网络(long short term memory，LSTM)建立的负荷预测模型效果更好。但是，这些模型训练需要大量的数据和高性能的GPU服务器，大大增加设备成本，很难在实际电力公司进行应用。因此，提出一种负荷在线预测方法，解决海量负荷数据的难以提取有效特征问题。LSSVM 对小样本建模时具有较高的预测精度，如果能够减少LSSVM 的训练时间进行在线更新建模，对利用海量数据进行负荷预测具有重要意义。

研究以某城市电网负荷数据为研究对象，采用偏最小二乘(partial least squares，PLS)算法对影响负荷波动的变量进行特征提取，将得到特征变量作为在线自适应最小二乘支持向量机(online adaptive least squares support vector machine，PAU-LSSVM)的输入变量，建立了电力负荷的PAU-LSSVM 模型。该模型能够根据负荷数据的波动通过更新矩阵在线优化LSSVM 参数，使整个模型处于动态实时更新中，具有较高的实效性和预测精度，适合工程应用。

1 在线自适应最小二乘支持向量机

1.1 最小二乘支持向量机原理

最小二乘支持向量机将二次规划问题转化为线性方程组的求解，降低了计算的复杂程度，在应用小样本建模时具有较高的预测精度和较强的泛化能力[18]。原理如下:

设训练样本集T＝，xi∈Rd，yi∈R，利用结构风险最小化原则，以误差的二次方为损失函数，优化问题可以转化为求解下面的问题。

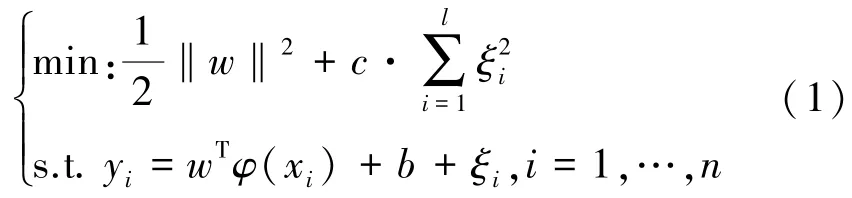
式中:w、b为模型参数；c为正规化参数；ξ为训练集预测误差向量；φ(·)为映射函数。

定义LSSVM 模型采用的核函数Kij＝K(xi，xj)，i，j＝1，2，…，n，满足Mercer 条件的任意对称函数。利用Lagrange 法将求解优化问题转化为求解线性方程组的问题:

式中:c为正规化参数，由模型参数计算得到。

LSSVM 模型参数a和b表达式如下所示:

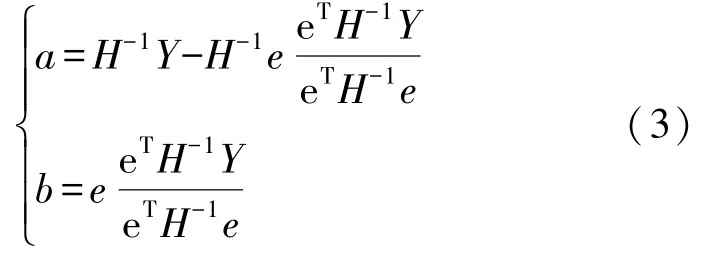
式中:Y为模型输出向量，Y＝[y1，…，yi，…，yn]T；eT＝[1，…，1]n×1；H为模型特征矩阵，表达式为

最后得到函数估计的LSSVM 模型为:

LSSVM 模型选用高斯径向基核函数构造，表达式如下:

式中:δ为核函数参数。

1.2 基于参数自适应更新的最小二乘支持向量机原理

参数自适应更新的最小二乘支持向量机(PAULSSVM)根据样本特性变化实时对LSSVM 的模型参数进行更新，保证参数与当前样本特性相一致。更新模型参数可以采用样本替换算法和样本添加算法。

在LSSVM 进行预测时，模型预测值＾yi与模型实际值yi的误差δ大于误差设定标准δs，模型失效，进行模型在线更新。误差表达式如下:

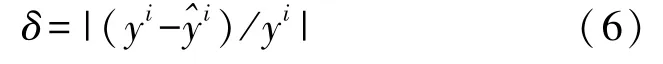
在对模型进行更新之前，应先对新输入样本进行判别，选择相应的模型更新方法，首先将样本进行归一化处理，然后计算新样本与训练样本的欧氏距离:

式中:p为变量个数，x0p为新样本的第p个变量；xip为训练样本的第p个变量。

如果d0k小于设定距离ds，选择样本替换算法更新模型，否则，选择样本添加算法更新模型。

(1)样本替换算法

样本替换算法是用新样本替换训练样本库中与之特性最为接近的一个样本。文中采用k-近邻算法确定与新样本特性最为接近的样本。得到训练样本中k个样本与新样本的欧氏距离，并计算k个样本的平均欧氏距离，k个样本中与平均欧式距离的距离最短的样本为与新样本特性最为接近的样本。

假设新样本(xr，yr)与训练样本中第i个样本(xi，yi)特性最为接近。用式(8)所示的gr代替模型特征矩阵H第i行，用代替模型特征矩阵H第i列，用K(xr，xr)+1/2c代替模型特征矩阵H第i行i列，因此得到更新的特征矩阵Hr。

将模型输出向量Y中的第i个元素yi用yr代替，得到Yr＝[y1，…，yr，…，yn]T，然后通过式(10)计算模型参数，使用计算的模型参数完成对模型的更新。

(2)样本添加算法

在样本添加算法中，将新样本(xr，yr)添加到训练样本中，将式(11)所示的gt和添加到模型特征矩阵H中，因此得到更新的特征矩阵Ht。

将yt加入到模型输出向量Y中，得到Yt＝[y1，…，yr，yt]T，然后通过式(13)计算模型参数，使用计算的模型参数完成对模型的更新。

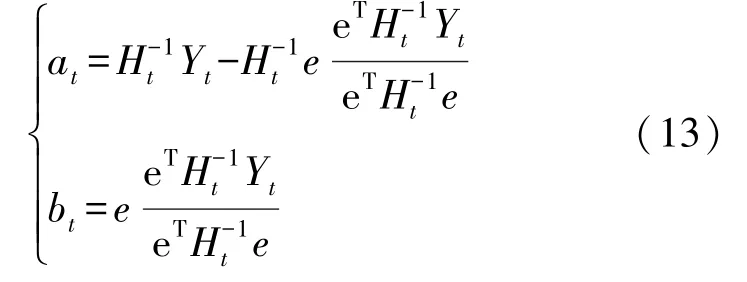
应用上述样本替换算法和样本添加算法对LSSVM 模型进行在线自适应更新，更新算法流程如图1 所示。

图1 OALSSVM 算法流程图

2 电力负荷变量选择

2.1 PLS 变量选择原理

文中采用刘林栋等[19]所述方法确定主成分，并通过当≥0.097 5 时交叉有效性确定需要提取的主成分个数。然后，使用变量投影重要性指标(variable importance in projection，VIP)计算出不同自变量对因变量y的贡献值，表达式如下:

式中:p为自变量个数，m为主成分的个数；r(y；th)为y与th的相关系数；whk为权值向量wh的第k个分量。

2.2 PLS 变量选择验证

考虑到电力负荷相关变量存在强耦合强相关的关系，文中使用杨婷婷等[20]燃煤锅炉运行数据进行对VIP指标有效性的验证，运行数据如表1 所示。

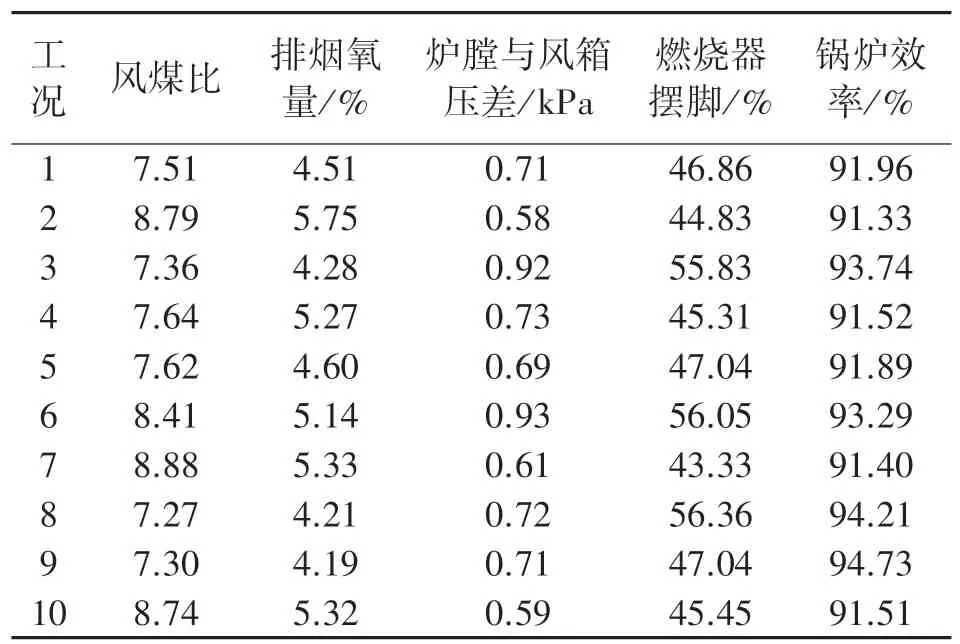
表1 燃煤锅炉运行数据

使用PLS 变量选择方法计算风煤比、排烟氧量、炉膛与风箱压差和燃烧器摆脚与锅炉效率的关系，得出VIP指标分别为0.934、1.144、0.883 和1.020。可以看出，排烟氧量和燃烧器摆脚对锅炉效率的影响相对较大，这与文献中糙集方法分析的结论一致，证明了文中VIP指标是有效的。

2.3 确定电力负荷特征变量

以某城市电网负荷数据为研究对象，考虑到季节和假期对负荷的影响，选择不同时间段的小时最高温度(Tmax)、日最低温度(Tmin)、平均温度(Taver)、平均风速(Vwind)、平均湿度(Haver)、平均降水量(Paver)作为PLS 输入变量，平均负荷为输出变量，使用PLS 变量选择方法对训练样本进行重要变量信息提取，各个变量的VIP如表2 所示。

表2 各输入变量的VIP

根据表2 所示，选择VIP值较大的最高温度、平均温度和平均湿度作为影响负荷的关键因素。

3 基于PAU-LSSVM 的负荷预测

3.1 PAU-LSSVM 负荷预测参数确定

选取某城市电网负荷数据进行仿真试验，选取一周历史运行数据，采样间隔为30 min，共计336 样本，再选取2 天数据96 个样本作为测试，用来检验LSSVM 模型的预测精度，部分电网运行数据如表所示。首先，将最高温度、平均温度和平均湿度等变量进行归一化[-1，1]，然后作为LSSVM 模型的输入，建立了电力负荷预测模型，LSSVM 初始模型参数使用改进遗传算法进行确定[21]，建模效果如图2 所示。

图2 LSSVM 负荷预测效果

为了进一步说明图2 展示的问题，计算每个测试样本与训练样本集的欧氏距离，欧氏距离分布在[0，2]区间内，将测试样本对应最小距离按照由小到大进行排序，并划分为5 个区间，并依据式(15)计算每个欧氏距离区间内的平均绝对百分比误差EMAPE，如表3 所示。

式中:M为区间内样本数量；为j时刻负荷预测值；x(k)为j时刻负荷实际值。

表3 中的“0”表示训练样本，可见，训练样本的预测误差较小，测试样本随着数量的增多，模型的预测精度在下降，甚至使模型失效。测试的96 个样本中仅有少数样本的预测误差可以满足要求，随着工况的迁移，大部分测试样本预测精度不能满足要求，因此，在线更新LSSVM 模型非常必要。根据表3 的试验数据，为了是模型的误差满足要求，确定PAULSSVM 模型中标准误差δs为3%，标准距离ds为1.5，样本替换算法中的k值取研究领域经典值[22]，令k＝5。

表3 LSSVM 负荷预测模型误差

3.2 构建PAU-LSSVM 负荷预测模型

基于PAU-LSSVM 方法建立的电力负荷预测模型结构图如图3 所示。

图3 PAU-LSSVM 负荷预测模型结构图

基于PAU-LSSVM 模型进行电力负荷预测，其中，该模型初始参数采用沙超等[21]所述的改进遗传算法确定，模型失效时，使用样本替换算法和样本追加算法进行参数更新，测试样本预测效果如图4 所示。可以看出，模型预测精度明显得到改善，随着测试样本的增加，模型仍具有较高的预测精度，体现了模型较强的泛化能力和工况迁移能力。经计算，模型更新时间几乎可以忽略，测试样本的平均绝对百分比误差为2.78%，小于3%，说明模型在线更新是有效的，能够实时捕捉负荷数据特征更新模型参数，保障模型预测精度。

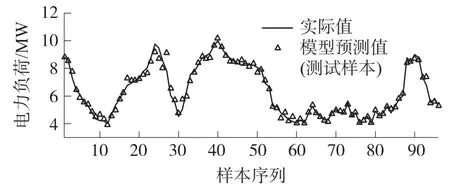
图4 PAU-LSSVM 负荷预测效果

文中进一步基于上述负荷数据建立了循环神经网络(RNN)、LSSVM 建立了负荷预测模型，所建的3 种模型输入变量均为基于PLS 提取的特征变量，其中，RNN 和LSTM 的隐含层数2，为了使两种深度神经网络能够更好的学习网络参数，将训练样本336 组数据增强为原来的20 倍，4 种模型预测效果如图5 所示。

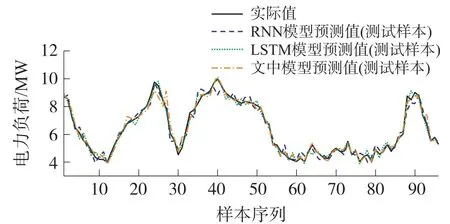
图5 不同模型负荷预测效果对比

从图中可以看出，PAU-LSSVM 模型预测曲线较深度神经网络RNN、LSTM 模型预测曲线波动小，经过计算，RNN 模型预测的平均绝对百分比为4.26%，LSTM 模型的平均绝对百分比为3.12%，略高于PAU-LSSVM 模型的2.78%。可见，该方法在预测精度上仍然具有一定的优势，并且可以在CPU 服务器上在线训练，工程实用价值较高。由于RNN 和LSTM 的负荷预测方法的预测精度与样本量的关系很大，在现有的研究中，一般而言，样本量与建模精度呈正相关，但也有极限。如果通过增加样本量来提高模型预测精度，又要考虑所需要的硬件资源。因此，结合样本量、模型算法、硬件计算能力多种因素，该方法更具有工程实用性和普适性。

3.3 负荷预测模型对比

考虑到负荷与季节、节假日有很大关系，选取某城市2018 年四个季节中的1 个月份以及节假日负荷数据为研究对象，训练样本由1 月份、5 月份、8 月份、10 月份的数据组成，样本采集间隔为1h，测试样本2 月份、6 月份、9 月份、11 月份的前半个月负荷数据组成，PAU-LSSVM 模型设定值不变。基于上述负荷数据分别建立LSTM、RNN、LSTM、PAU-LSSVM负荷预测模型，模型误差如表4 所示，可以看出PAU-LSSVM 预测大量测试样本时预测误差最小，说明模型能够适应工况迁移的问题，展示了模型较强的泛化能力和工程应用价值。

表4 不同建模方法对比

4 结论

提出了基于PAU-LSSVM 模型的电力负荷预测方法，主要结论如下:

(1)PAU-LSSVM 模型适合处理电力负荷预测中的非线性复杂建模问题，相比RNN、LSTM 等深度神经网络相比，在线更新耗时较短，在预测精度仍然具有一定的优势，适合工程应用。

(2)所提的PAU-LSSVM 模型能够根据样本变化特性进行在线建模，具有较高的数据处理能力和时效性。

(3)通过PLS 方法进行变量选择，压缩了建模所需变量的个数，降低了模型的维数和复杂程度，提高了预测精度。

(4)所提的PAU-LSSVM 负荷预测模型经过实际电网运行数据验证，模型能够解决工况迁移导致预测误差增大的问题，具有较高的工程应用价值。