基于EPCglobal 标准的多标签天线的RFID 通信建模*
陈光华张 勇
(1.四川邮电职业技术学院通信工程系,四川成都 610067;2.成都中医药大学医学信息工程学院,四川成都 610075)
射频识别(Radio Frequency Identification,RFID)[1]通常用于存在严重衰落的高散射环境中,这使得分集在这种通信场合中显得尤为重要;在RFID 技术中,通信是通过后向散射[2-3]进行的,其中连续波(Continuous Wave,CW)发送到标签并由其发射器反射,反射可以由发射器的接收功率驱动,因而无需电源。这使得该项技术非常方便廉价,因为标签不但尺寸小,而且可以大量生产。此外,它还可以提供几米以上的非视线(None Line of Sight,NLoS)通信。
无源RFID 标签的主要研究方向是提高读取精度和工作范围。为了对RFID 传播进行建模,需要在衰落信道的环境下进行。在这种情况下,可以采用具有莱斯分布(Rician-Distribution,RD)的衰落信道,但对于后向散射链路来说,这种模型只能提供粗糙的建模精度。因此,Wang 等[4]中引入了并矢后向散射信道,这种信道考虑了前向和后向链路的RFID 通信特性,这意味着更严重的衰落,且这种深度衰落显著地降低了系统的性能;佘开等[5]研究了前向与后向相关信道对系统识别性能的影响。将信道分为独立、相关和完全相关3 种情形,并基于广义莱斯衰落信道模型,推导出了识别率的解析计算式,给出了任意相关系数和多种信道条件下识别率统一的计算式。仿真实验表明,不同相关系数、信道条件、灵敏度和距离对识别率有影响;Yuechun 等[6]表明,对于某些星座来说,即使阅读器和标签之间的距离不是很大,读取速率也是非常差的;EPCglobal 通信系统[7-9]不支持任何前向纠错(Forward Error Correction,FEC),当系统工作在嘈杂的衰落信道中时,这就成为一个严重的问题;Kalaivani 等[10]、柳臻一等[11]针对基于空间-极化分集的多输入多输出(Multiple Input Multiple Output,MIMO)超高频RFID 系统进行了分析,建立了MIMO超高频RFID 系统信道模型,将OSTBC 编码应用于MIMO 超高频RFID 系统中,并对其编码性能进行了研究分析。实验结果表明,多个天线的使用明显提高了系统性能;Zhang 等[12]针对具有单输入多输出(Single Input Multiple Output,SIMO)和多输入单输出(Multiple Input Single Output,MISO)2 种情况的RFID后向散射系统,研究了前向和后向散射链路之间的信道相关性对误符号率(Symbol Error Rate,SER)的影响,并在任意相关Nakagami-m 衰落信道上比较了具有最大比合并(Maximum Ratio Combining,MRC)接收的SIMO 和MISO RFID 系统的性能,导出了M 元相移键控(M-PSK)和正交幅度调制(M-QAM)的渐近SER 的封闭表达式和上界。
研究在使用2 个标签天线即多输入单输出(Multiple Input Single Output,MISO)情形下的EPCglobal 传输协议的性能。结果表明,由于RFID 通信中信道星座的不利,采用EPCglobal 协议信号的可能分集增益(信噪比)不仅与信道模型和采用的编码方案有关,而且与前/后向链路的相关性及信道的空间相关性密切相关。
1 基于EPCglobal 标准的RFID 通信
所考虑的通信系统基于超高频RFID 传输的EPCglobal 标准[13],图1 所示为RFID 传输链路示意图。在传输过程中,阅读器发出一个CW,在这个波上,标签群的信息是脉冲间隔编码(Pulse Interval Encoded,PIE),并通过幅移键控(Amplitude Shift Keying,ASK)或相移键控(Phase Shift Keying,PSK)进行调制。
阅读器读取范围内的任何标签都将通过使用FM0 或Miller 子载波编码和ASK 调制反射输入的CW 来发回它的信息;由于标签对噪声的灵敏度较高,因此仅考虑标签对阅读器的后向散射响应。然而,前向和后向衰落值由于其在传输过程中的依赖性也被考虑在内;下面对图1 中标记区域标签信息的编码和解码进行讨论。
EPCglobal 标准包括2 种规格的后向散射数据编码。对于2 种编码来说,是将一个比特扩展到一个码片序列中,该序列被定义为若干个1/0 组合的序列,更多的码片意味着一个更鲁棒(抗干扰)但也更耗时的码组。最简单的就是FM0 编码,它是由描述2 个符号的边缘突变和1 个零比特符号的中间边缘变化来区分的。因此,1 个比特可以是有2 个码片值的FM0 编码。图2 所示为这种编码方案的状态图。

图1 RFID 传输链路示意图
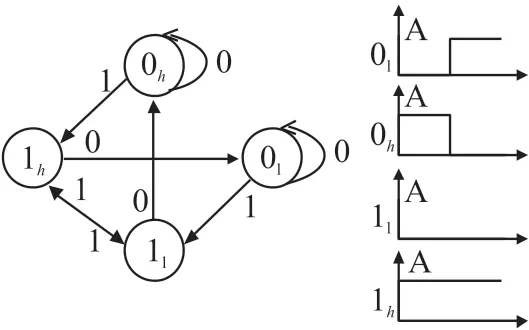
图2 FM0 编码状态图
对于Miller-M 子载波编码来说,相移发生在2个零符号的边缘上,而且在1 个符号的中间也存在相移。在这种情况下,相移意味着信号幅度不会从一个周期到另一个周期发生变化,图3 所示为这种编码方案的状态图,这里没有考虑子载波;在实际中,M表示用于编码1 个比特所用的周期数,其中每个符号需要发送t=2MT(M∈{2,4,8}),T是一个码片的时间周期。M=8 表示最鲁棒的但也是最耗时的传输模式。对于编码值的传输来说,数据是用每个码片持续时间T的值采样的。

图3 Miller 编码状态图
解码是通过噪声比特流与可能符号的相关性来完成的。对于该计算,接收到的ASK 信号被移位,因此高、低幅值电平具有相同的绝对值和不同的符号。此外,引入阈值At,其中每个接收到的大于阈值的码片值都设置为此阈值,即:
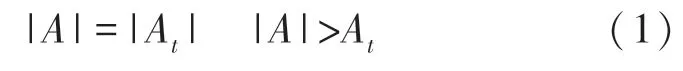
式中:这些码片由于非常严重的衰落而达到很高的幅值。深度衰落等效于高噪声,会极大地改变传输系统的幅值,从而对系统的性能有轻微的负面影响。
2 信道模型
信道可以通过采用归一化功率的特定衰落系数的发送符号的加权来建模,并通过一个加性白高斯噪声(Additive White Gaussian Noise,AWGN)信道发送。于是,信道方程为:

式中:发射符号s乘以一个复信道因子,并通过一个复AWGN 信道发送。的实部nr和虚部ni都是随机高斯数,且不相关,即:
式中:σ2表示复高斯噪声的方差/功率[14],a是表示信噪比(Signal to Noise Ratio,SNR)的一个因子:

式中:P表示平均信号功率,SNR 是以dB 为单位的信噪比。在中考虑信道的衰落,这一系数可以看作是AWGN 噪声中的一个因素,或者是减小AWGN噪声的一个因素。下面重点讨论基于上述信道模型的2 种信道结构。
2.1 Rician 信道
RFID 通信是在丰富的散射环境中进行的,在这种环境中,视线(Line of Sight,LoS)路径通常是可用的,为此采用Rician 信道模型。这种模型的信道因子有2 部分,实值视线部分和表示信号散射部分的复值NLoS 部分,这部分由一个复高斯随机数来表示,其特征与具有零均值和归一化功率的高斯噪声的随机数相同。这两部分之间的关系为:

式中:PLoS=K/(K+1)和PNLoS=1/(K+1)可以用Rician 因子K=PLoS/PNLoS来描述,K表征了LoS 的功率与NLoS 的功率分量之间的关系。

式中:I0为第一类零阶修正Bessel 函数。对于K=0,Rician 分布就变成一个瑞利分布,对于K→∞,分布变成一个在=1 的Dirac 分布,等价于一个AWGN信道。对于变量K来说,这种分布行为如图4 所示。

图4 不同K 值的Rician 分布数|h|的包络
2.2 并矢后向散射信道
尽管Rician 信道对于LoS 衰落信道来说是一种合适的模型,但它仅限于单向信道。由于来自于标签的RFID 通信是通过后向散射完成的,因此存在可用的前向和后向链路。在这种情形下,Rican 信道只能被看作是RFID 通信的一个粗略的模型。为了得到更精确的描述,应当考虑并矢后向散射信道。
这种信道可以描述为具有前向和后向链路的双向信道,2 个衰落系数为。对于每个链路的总衰落来说,可以由这2 个衰落系数相乘得到:

为了考虑前向和后向链路的统计相关性,引入链路相关性0≤ρ≤1,其中ρ=0 表示统计独立的前向/后向链路衰落,ρ=1 表示完全相关的前向/后向链路衰落,相当于。对于具有链路衰落相关性0<ρ<1 的信道特性来说,可以通过2个不相关瑞利衰落系数和(具有零均值和相等的方差)得到如下:

式中:Cov(·,·)是协方差算子,σf和σb为衰落值的标准偏差。在下文中,σf=σb=1 是有效的,同时在此假设下产生Rician 衰落系数,在这种情况下,首先计算瑞利数,然后用式(5)将瑞利数转换为Rician数[16];此外,在采用2 个标签天线的传输过程中,对于前向/后向链路相关性,还考虑空间相关性ρspa[17],ρspa的定义与ρ的定义方法相同。考虑有1 个阅读器和2 个标签天线通过一个并矢后向散射信道上的MISO 传输,则对于一个传输周期来说,衰落系数为:

为了区分并矢后向散射和单向信道的差别,要分别描述ρ=0 和ρ=1 时阅读器和标签天线之间的信道概率密度函数(Probability Density Function,PDF)。在这种情况下,后向散射信道中的2 个链路都具有瑞利分布衰落,其PDF 为[4]:

式中:Γ(·)为Gamma 函数,Kρ/(ρ+1)(·)为第二类修正贝塞尔函数,ρ/(ρ+1)为阶。
PDF 如图5 所示。后向散射信号的随机数往往有较小的值(<1),这相当于在传输过程中更大的破坏性衰落。此外,由于前向信道和后向信道的高度相关性,深度衰落就更明显。

图5 具有瑞利随机数的并矢后向散射分布的包络与正态瑞利分布的比较
3 发射分集技术及RFID 传播建模
3.1 发射分集技术
为了获得发射分集,对2 个发射天线应用Alamouti 方案[18],如图6 所示。表1 所示为这种传输的编码方案,其中2 个任意符号在一个定时周期t内通过2 个天线发送。在下一个时间段t+T,符号在2 个天线上切换,此外,对2 个符号取共轭,并对第一个符号反转。通过这种方法,可以在接收机中实现2 个符号的合并。
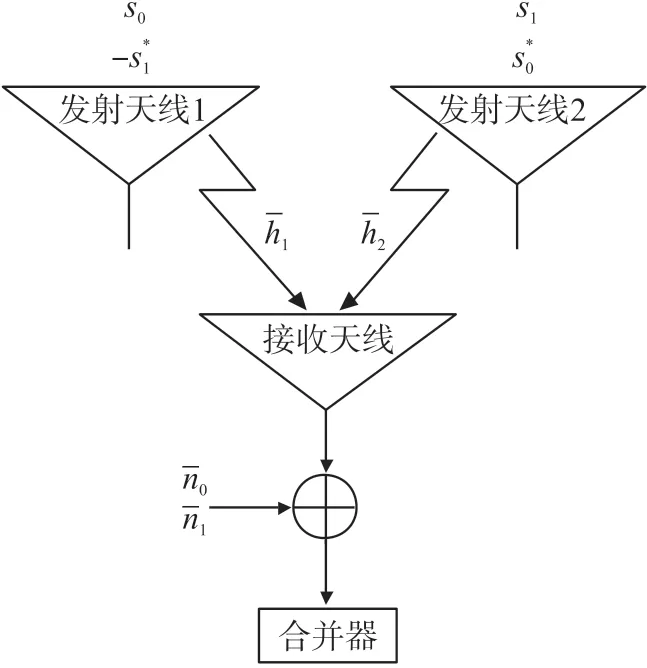
图6 采用2 个发射机和1 个接收机的Alamouti 方案传输

表1 发射分集编码方案
对于组合方案,假设在2 个定时周期内衰落为常数,则有:

基于这个假设和表1 中的编码就可得到接收信号如下:

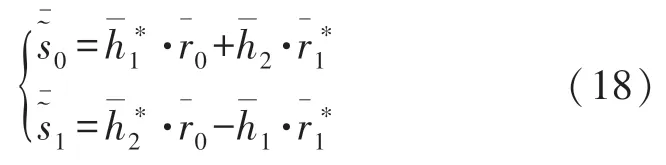
根据式(18),假设在接收机上有精确的信道估计,因此计算结果可以写为:
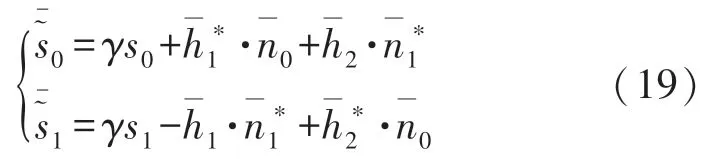
式中:γ是一个标量因子,它与衰落系数的大小成正比。在组合之后,就可以提取数据对。在本文中,分集方案是在信号调制之前采用的,因此2 个天线上的符号编码都是在码片级上进行的。在接收机上的信号组合之后,如第2 节所描述那样对比特进行解码。对于这种组合方案,假设发射天线完全同步,这对于带有多个天线的标签来说是成立的。
3.2 RFID 传播建模
根据EPCglobal 协议对RFID 传播进行建模。只考虑从标签到阅读器的后向散射传输,因为与前向链路相比,它对噪声的敏感性更高。对于后向散射传输来说,采用扩频序列对数据进行编码,将扩频后的数据进行ASK 调制,然后在信道上传输。作为对该协议的扩展,第4 节中描述的发射分集技术在数据调制之前在有2 个标签天线的传输情况下执行。随后,按式(11)~式(14)计算信道相关性。
为了比较分集增益,我们给出特定信道的信噪比(SNR)上的误码率(BER)。这里SNR 为一个发射和调制符号的能量Es与噪声功率谱密度N0的比值。值得注意的是,在MISO 传输过程中,在每个天线上使用一半的功率。假设后向散射比特的最大数目是根据EPCglobal 协议传输的,这意味着对于FM0 或Miller 子载波编码来说,在这些序列的前面有2 个前导码的采用16 比特的RN16 和采用528比特的EPC 分别有18 位或22 位。还假设如果准确检测到至少95%的前导码,则可以正确检测分组,检测到1 个信息位出错即表示分组出错。
4 仿真结果及分析
4.1 分集特性

图7 单向瑞利衰落信道中不同后向散射编码方案在SISO/MISO 及1 个阅读器天线传输时的BER 与SNR 的关系
图7 所示为单向瑞利衰落信道上不同后向散射编码方案和采用1 个(SISO) 标签天线或2 个(MISO)标签天线和1 个阅读器天线进行传输时的BER 与SNR 的关系曲线。可以看到,每种编码方案都存在分集增益,且分集增益随着码组的扩展减小而增大,即随着更鲁棒的编码序列而降低。如对于最鲁棒的Miller-8 编码来说,在SISO 和MISO 传输时,当BER=10-4时,获得的分集增益分别为13.3 dB和7.3 dB,而对于Miller-2 编码来说,在SISO 和MISO 传输时,当BER =10-4时,获得的分集增益分别为36.4 dB 和21.2 dB;较弱扩频序列的较好的分集性能是由于在传输过程中编码性能较低,所以对于更脆弱的扩频序列来说,分集潜力更大;在通常的超高频RFID 传输中,FM0 和Miller-2 码是最常见的扩频序列,因为传输速度更快;图8 所示为对于具有LoS 路径的K=3 的Rician 单向衰落信道得到的不同后向散射编码方案和采用1 个(SISO)标签天线或2 个(MISO)标签天线和1 个读取器天线进行传输时的BER 与SNR 的关系曲线,可以看到,在相同的BER 值时,分集增益相比于图7 的单向瑞利衰落信道,分集增益减小了1.0 dB~2.5 dB。

图8 Rician 单向衰落信道中不同后向散射编码方案在SISO/MISO 及1 个阅读器天线传输时的BER 与SNR 的关系
图9 所示为EPC 长度为528 位、不同后向散射编码方案以及在不相关前向和后向链路的并矢后向散射信道中采用1 个(SISO) 标签天线或2 个(MISO)标签天线和1 个阅读器天线传输时的BER与SNR 的关系曲线,前向和后向两个链路都为K=0.5 的Rician 分布。从图9 可以看到,完全不相关(ρ=ρspa=0)的并矢后向散射信道的分集增益相比于单向信道(图7 的单向瑞利衰落信道和图8 的Rician 单向信道)有增加,如当BER =10-2时,完全不相关的并矢后向散射信道对于Miller-2 编码来说,在SISO 和MISO 情形下,获得的分集增益分别为55 dB 和31 dB,而对于图7 的单向瑞利衰落信道和图8 的Rician 单向信道,获得的分集增益分别为17.5 dB 和10.9 dB(见图7)和11.2 dB 和7.5 dB(见图8)。与单向信道相比,这是由于由深度衰落所造成的损耗,使得RFID 通信的分集传输潜力变得非常明显;对于完全相关的前向和后向链路(ρ=1)和不相关的空间(ρspa=0)来说,增益也会增加,如图10 所示,图10 所示为EPC 长度为528 位、不同后向散射编码方案以及在完全相关的前向和后向链路的并矢后向散射信道中采用1 个(SISO)标签天线(SISO)或2 个(MISO)标签天线和1 个阅读器天线的传输的BER 与SNR 的关系曲线,前向和后向两个链路都为K=0.5 的Rician 分布。

图9 完全不相关的并矢后向散射信道中不同后向散射编码方案在SISO/MISO 及1 个阅读器天线传输时的BER 与SNR 的关系

图10 完全相关的前向和后向链路和不相关的空间的并矢后向散射信道中不同后向散射编码方案在SISO/MISO 及1 个阅读器天线传输时的BER 与SNR 的关系曲线
4.2 空间相关性
在图7~图10 的结果中,用于MISO 通信的2个发射信道是完全不相关的(即ρspa=0),但通常在RFID 通信过程中并不是这样,因为标签天线常常相隔很近[17],分集增益随着2 个发射路径(信道)相关性(空间相关性)的增大而减小。对于最大空间相关信道(ρspa=1),MISO 与SISO 传输相比,不能获得分集增益,因为2 个信道产生相同的信息。图11 所示为不同后向散射编码方案以及在前向链路和后向链路的相关系数为ρ=0.5 的并矢后向散射信道中采用1 个(SISO)标签天线或2 个(MISO)标签天线和1 个读取器天线传输时的BER 与SNR 的关系曲线。在MISO 传输过程中,2 个信道的空间相关系数为ρspa=0.5,2 个链路都为K=0.5 的Rician 分布。可以看到,与不相关的空间信道的图10 结果相比,分集增益明显下降了,但只要信道不完全相关,仍然可以获得分集增益。
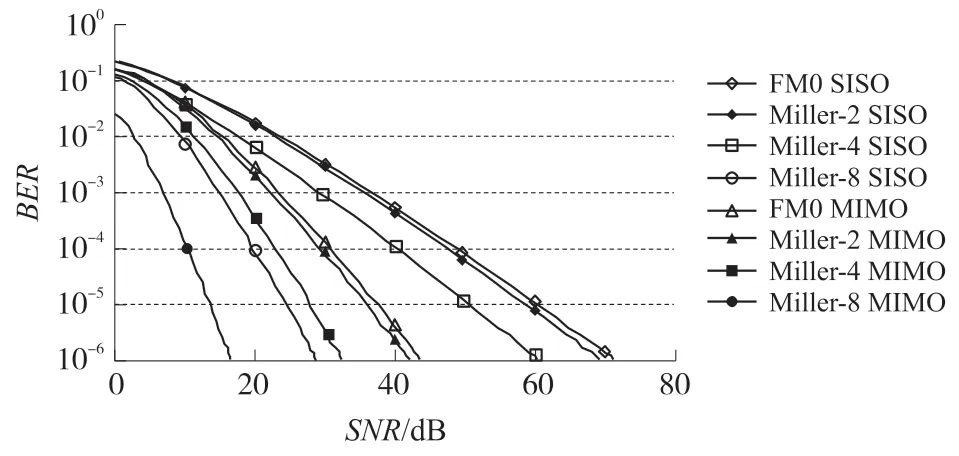
图11 不同后向散射编码方案以及前向链路和后向链路的相关系数为ρ=0.5 和两个信道的空间相关系数为ρspa=0.5 的并矢后向散射信道中SISO/MISO 及1 个阅读器天线传输时的BER 与SNR 的关系
图12 所示为具有LoS 分量(K=0.5)的并矢后向散射信道中的FM 0 编码信号传输采用2 个(MISO)标签天线对于不同的前/后向链路相关性及空间相关性的BER 与SNR 的关系曲线,其中空间相关性ρspa=1 等价于采用1 个(SISO)标签天线的传输。从图12 可以看到,相比于部分不相关链路和部分空间相关性(ρ=0、ρspa=0.8 或ρ=0.8、ρspa=0)的BER,不完全相关(ρ和ρspa=0.8),可以获得更高的增益。高相关链路(ρ=0.8)和完全相关链路(ρ=1)的增益明显高于不相关链路(ρ=0)和高相关链路(ρ=0.8)的增益;此外还可看到,空间相关性的变化比前向/后向链路相关性的变化获得的增益要低。可见,当空间相关性ρspa增大时,前向/后向链路ρ 的影响大于增益损失。信道性能随着空间相关性和前/后向链路相关性的增加而下降,因为当这2 个相关值很高时如ρ和ρspa>0.9,性能泄漏发生。
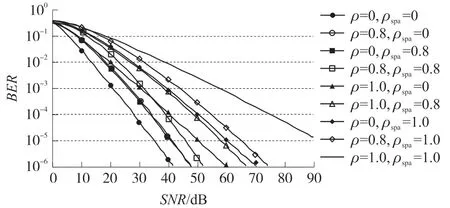
图12 具有LoS 分量(K=0.5)的并矢后向散射信道中FM0 编码信号对于不同的前/后向链路相关性及空间相关性的BER 与SNR 的关系曲线
5 结束语
研究了在EPCglobal 标准下的MISO UHF RFID后向散射传输的潜力。结果表明,增益随着信道的更高散射而增加。对于具有双向信道中的典型RFID通信来说,较大增益是通过完全相关的前向和后向链路来实现的;由于典型的RFID 小规模衰落链路具有并矢后向散射信道的特点,因而前向链路与后向链路之间的相关性相对较高,尤其是当阅读器的发射和接收天线相同时更是如此,这表明在这种情况下的RFID 系统中采用多个天线的标签有巨大的潜力。

