SynRM 混沌系统动力学特性分析及电路实现

安徽理工大学电气与信息工程学院 李泽宇

根据常微分方程与混沌系统动力学基本理论，采用混沌系统常用分析方法分析了SynRM混沌系统的基本动力学特性并根据系统方程完成了硬件电路设计。

现代混沌的观念包含着丰富的内涵至今没有完整、统一的定义，现有的定义也只是从不同的层面描述了混沌行为的特征。混沌作为一种物理现象在自然界中普遍存在，混沌运动具有自己独特的性质。具体表现在混沌系统的有界性、遍历性、分维性、确定系统的内在随机性、对初值的极端敏感性等。

混沌现象广泛存在于电力电子电路、电机等系统中。同步磁阻电动机具有结构简单，使用环境要求低，运行效率高和调速范围广等诸多优点。本文根据同步磁阻电动机的特点，建立了同步磁阻电机的动力学模型，经时间尺度变换和线性仿射变换得到同步磁阻电机（SynRM）混沌系统。采用数值模拟的方法做出了SynRM混沌系统的相图、分岔图和李雅普诺夫指数谱，分析了SynRM混沌系统的基本动力学特性并根据系统方程设计出硬件电路。

1 SynRM混沌系统

1.1 模型建立

SynRM混沌系统来源于同步磁阻电机（SynRM），在理想状态下，同步磁阻电机对应的系统方程式为：

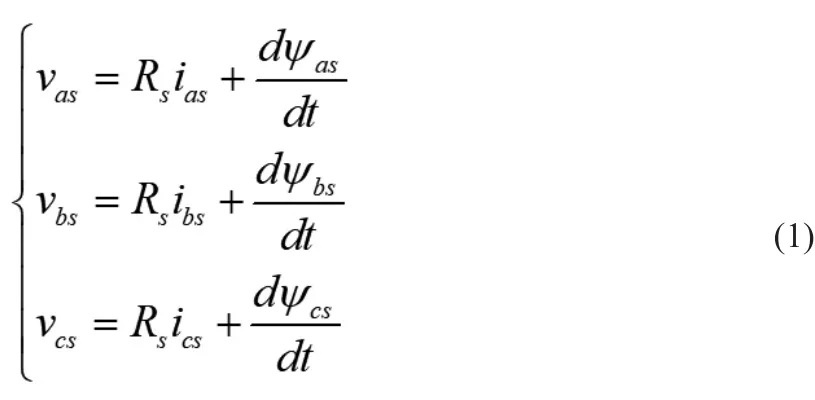
其中，vas、vbs、vcs为定子相电压，ias、ibs、ics为定子相电流，ψas、ψbs、ψcs为每相定子磁链，Rs为每相定子电阻。经过Park变换，公式(1)可改写为：

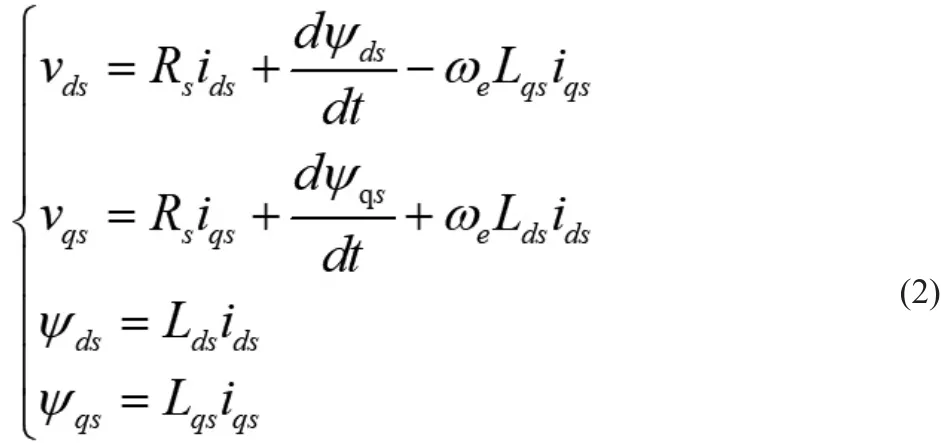
其中，vds、vqs分别表示电压的直轴（d轴）和交轴（q轴）分量，ids、iqs分别表示电流的d轴和q轴分量，Lds、Lqs分别表示电感的d轴和q轴分量，ψds、ψqs分别表示磁链的d轴和q轴分量，ωe为同步磁阻电机转子角速度。

同步磁阻电机电磁转矩方程描述如下：

其中，P为电机极数，Te为电磁转矩。

同步磁阻电机运动方程描述如下：

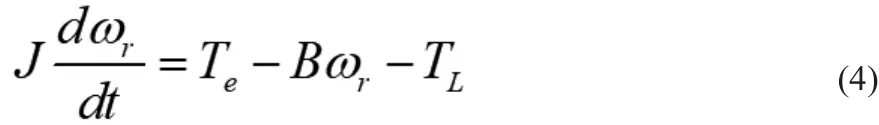
其中，ωr为转子转速，J为转动惯量，B为粘滞系数，Tl为负载转矩。

图1 系统(7)相轨迹图

由公式(2)，(3)，(4)可得同步磁阻电机的动力学模型：

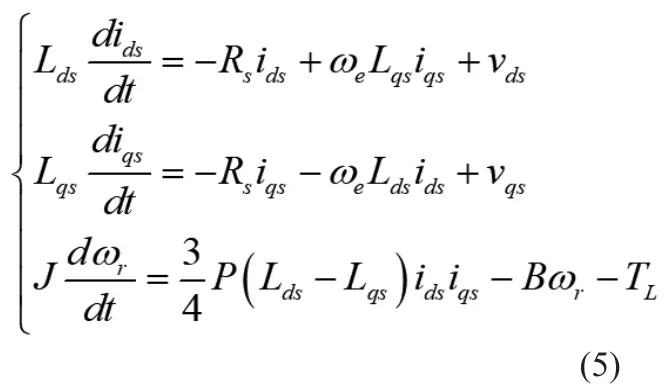
经时间尺度变换和线性仿射变换得到同步磁阻电机无量纲状态模型。

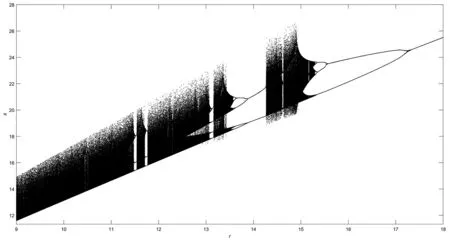
图2 参数r变化时系统(7)的分岔图

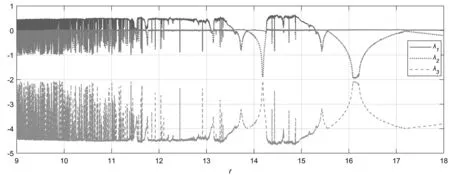
图3 系统(7)的李雅普诺夫指数图

表1 平衡点的稳定性

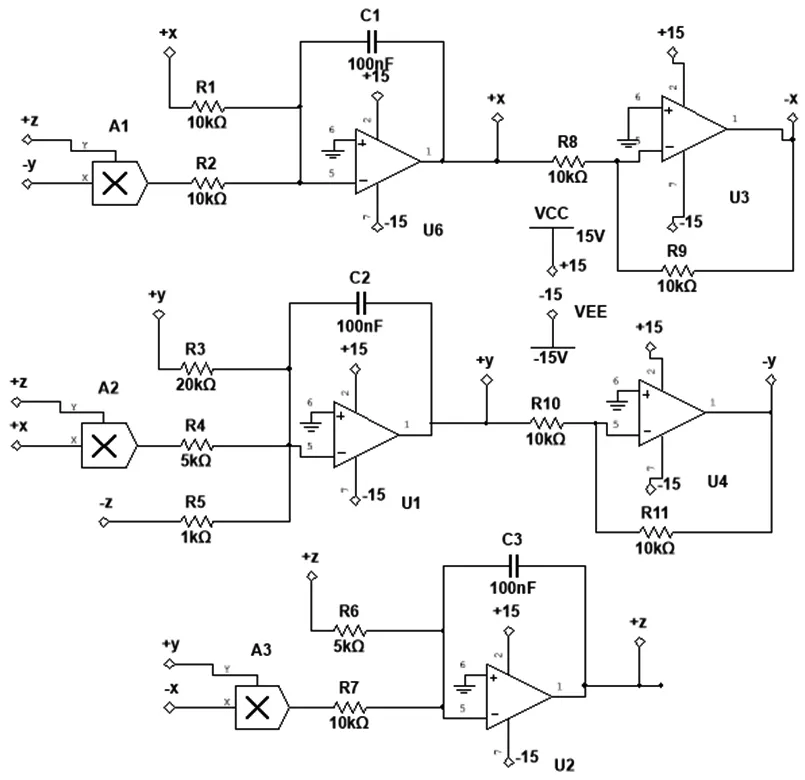
图4 电路原理图

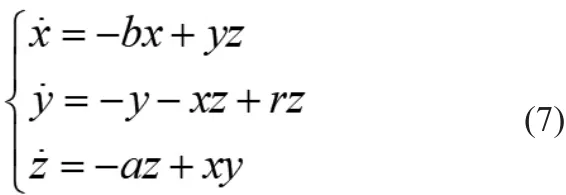
公式(7)即为无量纲SynRM混沌系统的数学模型，下面对如公式(7)所示无量纲SynRM混沌系统系统进行动力学特性分析。

1.2 SynRM混沌系统特性分析

该混沌系统存在五个平衡点：S0（0，0，0），S1,2（0.2042，±1.4142，±0.1444），S3,4（9.7958，±1.4142，±6.9267），对应平衡点稳定性如表1所示。选取参数a，b，r分别为，a=2，b=1，r=10时，系统存在混沌吸引子，输入初值x=2，y=3，z=1，相轨迹图如图1所示。

当a=2，b=1，r∈[9，18]时，系统(7)关于x轴方向的分岔图如图2所示，系统(7)的李雅普诺夫指数图谱如图3所示，该系统存在混沌现象。

2 电路实现

采用模块化设计方法设计模拟电路，验证系统的动态行为，系统由运算放大器、模拟乘法器等电子元件构成。

由于系统(7)状态变量的变化范围超出模拟元器件允许的电压范围，且为便于在电路输出信号中观察到混沌现象，需对原系统进行变量比例压缩变换和时间尺度变换。所得方程如下：

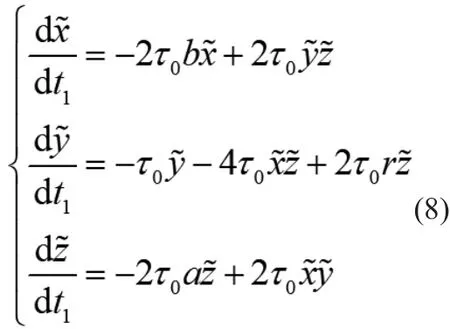
其中t=τ0t1，，a=2，b=1，r=10，τ0=500，所设计电路如图4所示。

结论：采用数值模拟的方法做出了SynRM混沌系统的相图、分岔图和李雅普诺夫指数谱，分析了SynRM混沌系统的基本动力学特性并根据系统方程设计出硬件电路，仿真结果表明SynRM混沌系统中存在混沌现象。