正交多相码波形设计方法

西安电子工程研究所 扈月松 史小斌 杨千禾 张苡宁

数字阵列雷达通过发射、接收和分离正交波形实现多目标搜索和跟踪，而雷达正交波形的正交性对后续的数据处理环节有很大影响。研究序列二次规划算法、代数法两种正交波形产生方法后，提出了自适应遗传算法产生正交波形的方法，并分别阐述了三种方法的优缺点和改进点。

数字阵列雷达是雷达发展的方向之一，它通过发射、接收和分离正交波形实现多目标搜索和跟踪。相比于传统的相控阵雷达，数字阵列雷达有更强的多目标搜索和跟踪能力，更高的距离分辨力。

数字阵列雷达的波形需要使用正交波形来抑制不同目标回波的互相干扰，实现从回波中提取每一个目标的独立信息。波形的正交性极大的影响了后续的脉冲压缩及恒虚警处理环节。在数学上一般用自相关旁瓣峰值和互相关峰值来描述波形的正交性。

2004年，Deng采用了模拟退火算法设计了正交四相码波形，自相关旁瓣峰值为-14.8dB，互相关峰值为-13.5dB；2006年，刘波等使用遗传算法设计的正交波形进一步降低了信号的自相关旁瓣峰值和互相关峰值；2011年，胡亮兵采用约束非线性规划算法设计的正交多相码，其正交性优于文献；2014年吉林大学孙明亮使用混沌序列设计二相编码信号，运算速度和波形的多样性都有了提升。

本文拟对正交多相码波形设计的遗传算法，序列二次规划算法和代数法三种方法进行研究，分别仿真得到正交多相码波形，并在波形的正交性、算法的复杂度等方面比较三种算法的优缺点，提出三种算法的改进方法。

1 数学模型

一般的相位编码信号形式为u(t)=a(t)ejφ(t)，其中a(t)为矩形脉冲，φ(t)为信号的相位。假设一个正交数字阵列雷达有L个子阵，每个子阵的发射天线发射一个正交信号集中的不同正交信号。若信号集种所有的正交信号符合一般的相位编码信号形式，且为恒模信号，则该信号集形式为。

正交信号重要的性质之一是正交性，与它相关的两个参数如式(1)所示，其中A(φl,k)为自相关函数，C(φp,φq,k)为互相关函数。

理想状态下，A(φl,k)和C(φp,φq,k)需要满足波形的自相关旁瓣峰值均为0，波形的互相关峰值均为0。但在实际信号中，不存在完全正交的一组正交信号，所以在设计时只能让波形的自相关旁瓣峰值和互相关峰值或者自相关积分旁瓣能量和互相关积分能量尽量小，如式(2)所示。

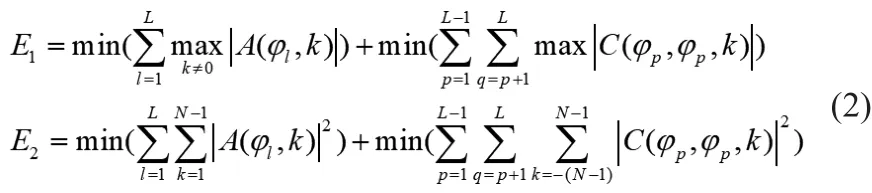
式(2)中E1为极小化峰值电平准则，E2为极小化积分旁瓣能量准则。在实际设计中，因为设计要求不同可以选择不同准则使用。本文中将介绍两种正交多相码波形设计的方法，以及在传统遗传算法基础上改进的自适应遗传算法方法。

2 序列二次规划（SQP）算法

准则E1和E2是带约束的非线性规划问题，SQP算法是一种解决非线性规划问题非常有效的算法，它的形式如式(3)所示。

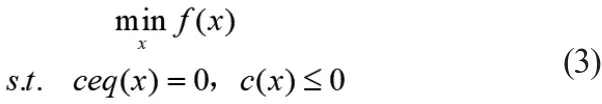
式(3)中f(x)为目标函数，ceq(x)是等式约束条件，c(x)是不等式约束。应用在设计正交连续相位波形中，问题模型变形后如式(4)所示。

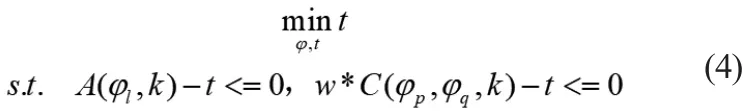
式(4)中t为辅助变量，也是目标函数。w为一可调参数，当设计要求自相关峰值旁瓣较低时则w＜1，要求互相关峰值较低时则w≥1。SQP算法通过该模型可以设计出正交连续相位编码。

仿真验证时，假设信号组中的正交波形个数为L=4，每个信号的编码长度为N= 40，参数w=1。使用matlab中的fmincon函数进行序列二次规划算法仿真设计正交多相码波形设计，最终得到的信号组中所有信号的自相关函数和互相关函数图如图1所示。从图中可以看出，使用SQP算法设计的正交连续相位编码信号组中信号的自相关旁瓣峰值为-17.48dB，互相关函数旁瓣峰值为-17.48dB，自相关性和互相关性都非常好。

SQP算法的缺点是计算量巨大，且只能设计连续相位编码信号。在SQP算法计算过程中涉及到求解海森矩阵等复杂运算，因此当信号组中信号数L增大或者相位编码数N增大时，SQP算法的时间复杂度和空间复杂度会大大增加。解决这一问题的关键在于寻找算法过程中替代求解海森矩阵的算法，比如使用线性拟合，这样可以大大降低SQP算法的时间复杂度。

3 代数法

代数法通过求解k阶本原多项式，进而得到一系列序列码如最长序列码M和序列族F等等来设计正交相位编码。代数法避免了数值优化的过程，在计算量、效率和空间复杂度上占有优势。最长序列码M是正交二相编码，序列族F是正交四相编码，本文中为了方便与其他两种算法进行比较，选择序列族F进行研究。

图1 SQP算法得到的正交信号组的归一化自相关函数和互相关函数图

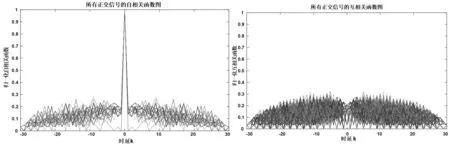
图2 代数法得到的正交信号组的归一化自相关函数图

序列组F的产生是由本原多项式开始的。假设Z2是以2为模的余数集{0,1},Z2[x]是以Z2为系数的多项式集合。Z2(x)中的不可约多项式称为本原多项式。若本原多项式的最高阶数为k，则称该本原多项式为k阶本原多项式。Z4是以4为模的余数集{0,1,2,3}，Z4(x)是以Z4为系数的多项式集合。将Z4(x)的系数进行模2运算，得到对应的Z2(x)多项式，这一操作称为规约。与之对应的，由Z2(x)得到Z4(x)的操作称为逆规约。

为了得到序列族F，需要将本原多项式经过如下步骤操作：

（1）将Z2(x)中的k阶本原多项式通过逆规约得到f(x)。

（2）接着令H(x2) =f(x)f(－x)，再对H(x2)进行变量代换得到H(x)。

（3）当k为偶数时，令P(x) =H(x)；当k为奇数时，令P(x) =－H(x)。

（4）再求解以P(x)为特征多项式的线性迭代方程，最终得到一组序列族F编码。这一过程可以用移位寄存器的方法实现。

（5）将序列族F编码通过映射关系exp(j{0,1,2,3}/4*2π)变为相位形式编码，就得到了我们最终需要的正交信号编码。

序列族F可以设计的正交信号个数L=2k+1和正交信号编码长度N=2k－1也与本原多项的最高阶数k有关。

仿真验证时，通过matlab的gfprimfd函数产生一个k=5的5阶本原多项式g(x)=x5+x2+1，再由g(x)产生多项式P(x)=x5+3x2+2x+3。用matlab实现移位寄存器来求解以P(x)为特征多项式的线性迭代方程得到序列族F，通过映射关系由该序列族F得到了一组正交信号相位编码。该信号组相位编码长度N=25－1=31，信号组中信号数L=25+1。

信号组中所有信号的自相关函数和互相关函数如图2所示。信号组的所有正交信号的自相关旁瓣峰值平均值为-12.93dB，所有正交信号间的互相关峰值平均值为-12.04dB。

尽管代数法设计的信号在自相关和互相关性能上不及SQP算法，但是在算法时间和空间消耗上远远优于SQP算法。上述代数法在仿真耗时不超过1s，而如果使用SQP算法设计正交信号数为L= 33,N= 31的正交信号组，耗时将至少是代数法耗时的105倍，空间消耗同样更加巨大。而且随着正交信号数量需求L增大，理论上信号组的整体正交性必然会降低，两种算法结果的正交性差距会越来越小。所以代数法适合正交信号数较大，信号长度较长的正交离散相位编码设计。代数法的关键在于如何设计出更好的编码，使得映射后得到的正交信号组正交性更好，比如应用混沌序列，多相互补码等等。

图3 遗传算法得到的正交信号组的归一化自相关函数图

4 自适应遗传算法

SQP算法和代数法在设计正交波形问题上均有波形类型的限制，在智能算法中，遗传算法对解决准则E1和E2这类复杂的非线性优化问题有较好的效果，并且遗传算法设计正交波形自由性更大。参考传统遗传算法，将每个信号集S作为算法中的个体，信号集中的正交波形作为染色体，波形信号中的相位编码作为基因。为了尽可能降低信号的自相关旁瓣峰值和互相关峰值，结合准则E1和E2，使用式(5)作为算法的代价函数：

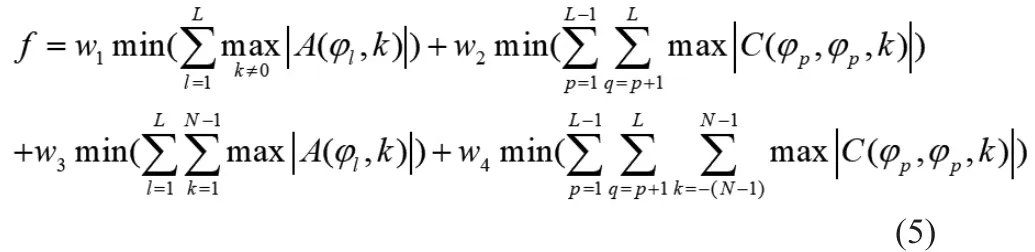
式(5)中[w1,w2,w3,w4]为权值，其数值需要根据实际情况进行调整。如果想要自相关性更高的波形，则需要增大w1,w3权值；如果需要互相关性更高的波形，则需要增大w2,w4的权值。

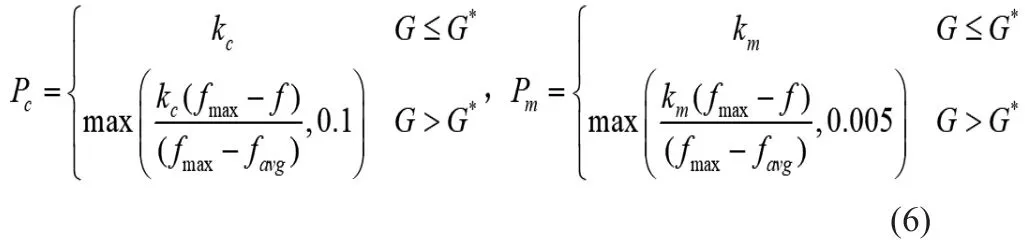
本文中为了使遗传算法中的进化速度加快，同时避免遗传算法陷入过早陷入局部最优解，加入了自适应算子，将交叉概率Pc和变异概率Pm做如式(6)调整，这样使得算法在前期产生多种变异和组合，后期可在小范围内搜索最优解。

在基因变异环节和基因交换中使用了父子竞争法，使得每次变异和交换环节产生种只有正交性较好的新个体才能进入新种群，进一步加快了算法的收敛性。但这样做可能会破坏群体的活性，因此在最佳个体选择环节中每次新增少数随机生成的新个体，避免群体收敛过快陷入局部最优解。在算法中最佳个体长期无法进化的时候，使用贪心算法强制对最佳个体的每一位基因改变，并观察正交性是否更佳，使得算法在后期也可以让最佳个体进化，产生更好的正交波形。

通过上述自适应遗传算法可以产生任意相位的正交多相码波形，本文为了方便和上述方法进行比较，选择产生正交四相码波形。

仿真验证时，假设信号组中的正交波形个数为L=4，信号编码长度为N=40，相位编码方式为离散四相编码。给定遗传算法种群总数P=500，算法迭代次数G=1000，权值[w1,w2,w3,w4]为[10, 20, 4, 3]。最终得到的信号组中所有信号的自相关函数和互相关函数如图3所示。从图中可以看出，本文设计使用的自适应遗传算法的自相关旁瓣峰值最大值为-16.76dB，互相关峰值最大值为-13.72dB，正交性较好。

遗传算法设计正交信号的最大特点是较为灵活。通过修改代价函数，遗传算法可以设计任意波形个数L、任意信号编码长度N和任意相位数M的正交波形信号组，还可以实现信号的多普勒敏感性改善等功能。缺点是算法的效果较为一般，且算法耗时较长。遗传算法可以通过增大信号编码长度N、展宽主瓣和增加信号的相位数M，增强信号的正交性。

结束语：本文仿真和比较了两种现有的正交多项码波形设计方法，并提出了设计性更加灵活的自适应遗传算法。其中SQP算法设计的正交信号组在正交性上表现最好，但是只能设计连续相位编码信号，且时间空间复杂度较高。代数法时间空间复杂度最低，可以实现在线设计，但目前只能设计正交二相码或正交四相码等正交离散编码信号，且信号编码长度N只可取固定几种值。自适应遗传算法比较灵活，可以设定任意信号数目L、信号相位数M和信号编码长度N的正交相位编码信号组，但信号组正交性较为一般。为了加快算法的进化速度，同时避免算法过早陷入局部最优解，本文采用了自适应算子，父子竞争法和贪心算法等对遗传算法进行改进，改进后的算法产生正交波形的速度更快，正交性更好。三种方法各有利弊，需要在实际应用中斟酌使用。