内涵型NGM(1,1,K)预测模型及其在油液光谱分析中的应用

王海涛 龚烈航

(1.广东机电职业技术学院 广东广州 510080；2.陆军工程大学野战工程学院 江苏南京210000)

油液光谱分析是利用各种金属元素的原子在迁跃过程中发射或吸收不同的光谱波长来了解液压油中所含金属元素的种类及含量，从而了解零件磨损状况，判断机械异常和预测故障的一种方法[1]。目前已广泛应用于航空、铁路、军事等许多重要部门。油液分析数据具有记忆性强、依时间连续变化的特点，通过预测未来数据的变化趋势结合油液分析数据的阈值，能够较早发现液压系统的故障征兆，避免更严重事故的发生，对保障设备正常运行具有极其重要的意义[2-6]。

依靠油液分析数据预测液压系统的运行状态时，因对液压系统内部的磨损及运行细节所知甚少，有理由认为液压系统为一灰色系统[7]。另外，油样的采集、测试过程相对复杂，成本高，油液样本相对较少。灰色预测模型所需数据样本少，无需考虑待预测系统的状态参数，仅依靠数据本身去预测系统未来状态的发展趋势，且具有较高的预测精度，因此，文中选择灰色预测模型作为预测工具。

灰色系统理论是研究少数据、不确定性的理论，自1982年邓聚龙教授创立灰色系统理论以来，已广泛应用于社会经济、工业、农业等领域，并取得了显著的成果[8-9]。GM(1,1)模型作为灰色系统理论的核心内容，是应用最广泛的灰色预测模型[10]。作为GM(1,1)模型的拓广，文献[11]提出了新灰色预测NGM(1,1,K)模型，称之为新NGM(1,1,K)模型。但在应用新NGM(1,1,K)模型时，出现拟合与预测精度不高的情况，甚至不如传统GM(1,1)模型。通过分析其建模机制，得出其精度不高的原因为：新NGM(1,1,K)模型的定义型与白化型不匹配。为消除因不匹配问题而引起的固有偏差，本文作者在新NGM(1,1,K)模型的基础上，提出了内涵型NGM(1,1,K)模型。

1 内涵型NGM(1,1,K)模型的建立

1.1 新NGM(1,1,K)模型

为了便于与后文提到的内涵型NGM(1,1,K)模型进行比较分析，对新NGM(1,1,K)模型[11]的建模过程作简要介绍：

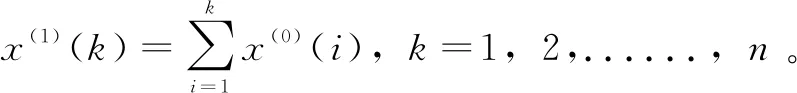
建立基于非齐次指数律特性离散数据序列的新NGM(1,1,K)模型的定义型：

x(0)(k)+az(1)(k)=kb+c

(1)

式中：z(1)(k)称为模型的紧邻均值生成背景值序列，

k=2,3,......,n

(2)

式(1)的一阶白化微分方程

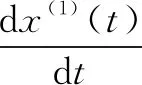
(3)

称为新NGM(1,1,K)模型的白化型。

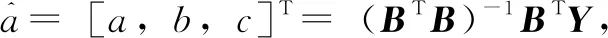
(4)

将参数a、b和c代入一阶白化微分方程(3)，取初始条件为：x(1)(1)=x(0)(1)，可得x(1)的响应函数：

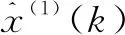
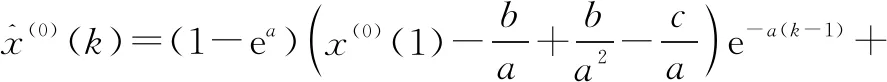
(5)

当k≤n时，所得值为原始数据的拟合值；当k>n时，所得值为原始数据的预测值。

1.2 新NGM(1,1,K)模型偏差原因分析

新NGM(1,1,K)模型的建模机制为：先用定义型(1)估计参数a、b和c，再将其代入白化响应式(5)中进行拟合与预测计算。然而，定义型(1)与白化型(3)是有差异的，存在不匹配问题。

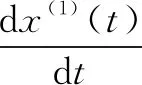
即：

(6)

将新NGM(1,1,K)模型的定义型x(0)(k)+az(1)(k)=kb+c与式(6)比较，可知其白化型与定义型存在两处不匹配：

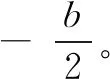
上述两处不匹配造成了新NGM(1,1,K)模型的固有偏差。文献[8]指出GM(1,1)白化型并不是从定义型推导出来的，仅仅是一种“借用”、“白化默认”。文献[12]深入分析了GM(1,1)模型的白化型和定义型中所含参数a和b的关系，得出2种形式下的参数是有差异的。同理，新NGM(1,1,K)模型存在同样的问题，其原因可以归结为：新NGM(1,1,K)模型的定义型与白化型不匹配，从而导致拟合与预测结果的失效。

1.3 内涵型NGM(1,1,K)模型

为解决新NGM(1,1,K)模型的定义型与白化型不匹配问题，消除其固有偏差，文中提出内涵型NGM(1,1,K)模型。

设x(0)为原始序列，x(1)为其一次累加生成序列，对x(0)建立如下模型，记为内涵型NGM(1,1,K)模型：

其中，a、b和c为待定参数，由公式(4)求得。

证明：基于新NGM(1,1,K)模型的定义型：

x(0)(k)+az(1)(k)=kb+c

以z(1)(k)的表达式：

代入有：

x(0)(k)+0.5a(x(1)(k)+x(1)(k-1))=kb+c

以x(1)(k)的表达式：

x(1)(k)=x(0)(k)+x(1)(k-1)

代入上式有：

x(0)(k)+0.5a(x(0)(k)+2x(1)(k-1))=kb+c

可转化为

(1+0.5a)x(0)(k)+ax(1)(k-1)=kb+c

令k=2有：

(1+0.5a)x(0)(2)+ax(1)(1)=2b+c，

联合考虑

(1+0.5a)x(0)(k)+ax(1)(k-1)=kb+c

(7)

(1+0.5a)x(0)(k-1)+ax(1)(k-2)=

(k-1)b+c

(8)

从式(7)有：

(9)

从式(8)有

(10)

将式(10)代入式(9)有

(11)

式(11)也适合

从而有：

依此类推可得：

(12)

已知k=2时，新NGM(1,1,K)模型的定义型为

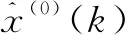
(13)

由此可见，内涵型NGM(1,1,K)模型是从新NGM(1,1,K)模型的定义型推导出来的，故与定义型存在零偏差。

2 模型在油液光谱分析中的应用

监测试验在某型挖掘机液压系统上进行，取样点位于回油管的取样球阀处，对所采集到的油样在测量之前，做如下预处理：

(1)采用超声波振荡器振荡油液；

(2)将油液温度加热到50 ℃;

(3)采用超声波清洗仪除气泡。

对油样做发射光谱分析，得到的Fe元素质量分数原始数据如表1所示。以前4次Fe元素质量分数为建模数据，分别建立内涵型NGM(1,1,K)模型、新NGM(1,1,K)模型和传统GM(1,1)模型以预测第5次、第6次和第7次Fe元素质量分数，其拟合、预测结果如表2所示。

以Fe元素质量分数序列建立的内涵型NGM(1,1,K)模型，其响应式为

建立的NGM(1,1,K)模型，其响应式为

k=1,2,......,n

建立的传统GM(1,1)模型，其响应式为

表1 Fe元素质量分数原始数据

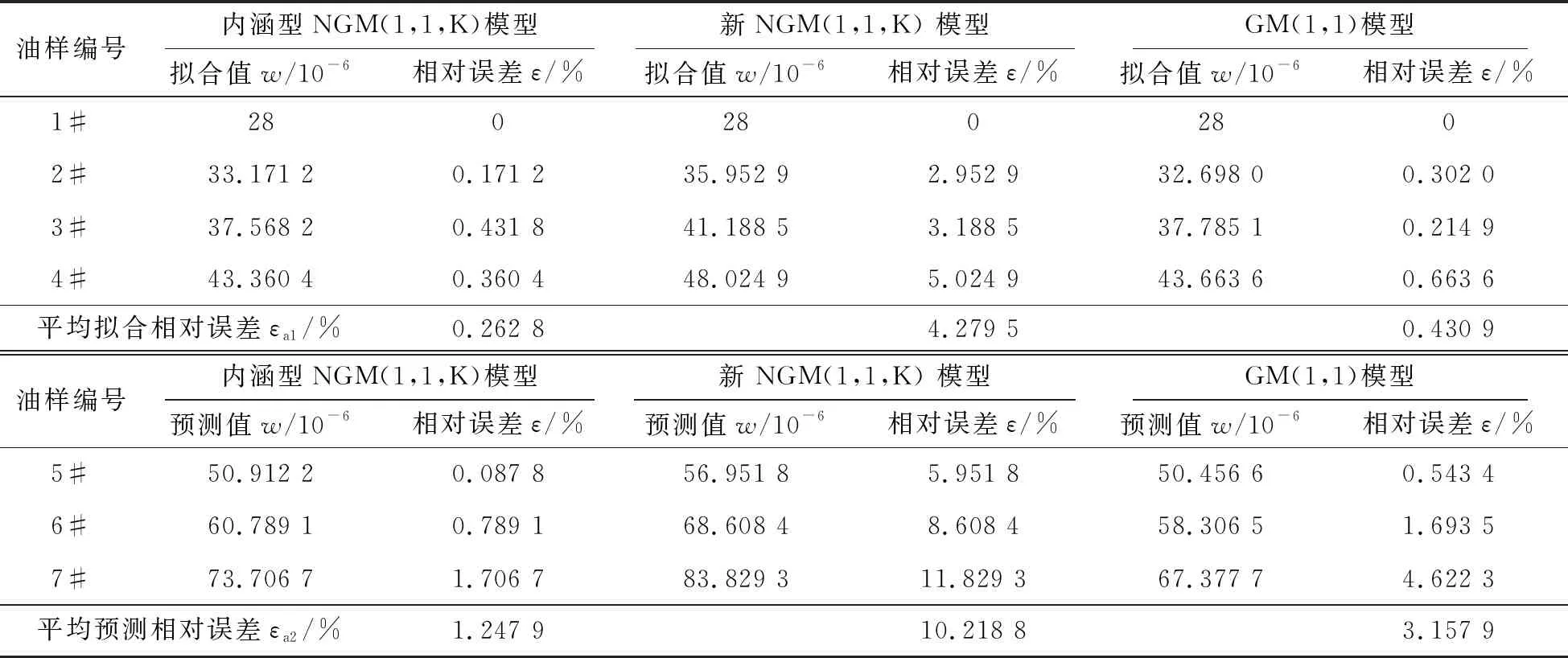
表2 3种模型精度比较

由表2可知：拟合精度方面，内涵型NGM(1,1,K)的平均拟合相对误差为0.262 8%，新NGM(1,1,K)模型的平均拟合相对误差为4.279 5%,GM(1,1)模型的平均拟合相对误差为0.430 9%；预测精度方面，内涵型NGM(1,1,K)模型的平均预测相对误差为1.247 9%，新NGM(1,1,K)模型的平均预测相对误差为10.218 8%，GM(1,1)模型的平均预测相对误差为3.157 9%。3种模型的预测曲线如图1所示，内涵型NGM(1,1,K)模型可以很好地预测Fe元素质量分数的变化，新NGM(1,1,K)模型预测值偏大，GM(1,1)模型预测值偏小。由此可见，文中提出的内涵型NGM(1,1,K)模型预测精度最高，其次是GM(1,1)模型，精度最差的是新NGM(1,1,K)模型。

结合光谱分析阈值制定方法[13]，得到液压系统Fe元素质量分数的正常值、警戒值和异常值界限如图1所示。新NGM(1,1,K)模型预测值偏大，根据液压系统维护规则，会造成过度维护，浪费资源；GM(1,1)模型预测值偏小，会造成维护不到位，而后引发故障。内涵型NGM(1,1,K)模型预测第6次取样Fe元素质量分数为6.078 91×10-5，处于正常值界限以下。第6次取样实测值为6×10-5，预测第7次取样值为7.370 67×10-5，超过正常值界限，预示液压系统将要面临不正常磨损，要对液压系统进行体外循环过滤或停机检查，防止故障发生。

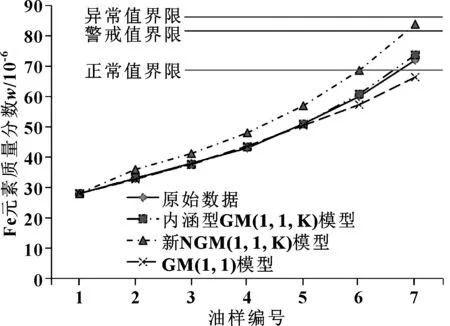
图1 3种模型预测曲线

3 结论

(1)针对新NGM(1,1,K)白化型与定义型存在不匹配的问题，提出了内涵型NGM(1,1,K)灰色预测模型。将该模型对某型挖掘机液压系统光谱分析Fe元素质量分数序列进行建模，与GM(1,1)模型和新NGM(1,1,K)模型相比，该模型具有更高的拟合与预测精度。

(2)内涵型NGM(1,1,K)模型得到的光谱分析元素质量分数的预测值结合阈值制定结果可实现对液压系统的状态监测，做到主动维护，保障其可靠运行，防止故障发生。