旋转尾管悬挂器轴承密封圈的有限元分析及结构优化*

张 满 李伟青 齐晓晨

(中国地质大学(北京)工程技术学院 北京 100083)

轴承是旋转尾管悬挂器的关键部件。在旋转尾管固井过程中，该轴承需要在高载荷、高温、高压、泥浆环境下进行旋转，属于在特重载荷和极端恶劣工况下工作的特种轴承。在如此恶劣的条件下工作，如果轴承密封不严，泥浆及其他杂物将进入轴承中，将加速轴承的磨损，并影响其性能和寿命，从而造成旋转尾管悬挂器不能顺利工作[1]。旋转尾管悬挂器轴承的密封结构属于接触型密封，接触型密封圈包括O形和唇形密封圈。其中，Y形密封圈因为其密封性好，磨损能力强且工作稳定，更适合用于旋转尾管悬挂器轴承的密封。通过设计Y形密封圈的最优尺寸参数，增强密封圈的密封效果，这对轴承的密封具有积极意义。

本文作者根据该类轴承的结构特点和工况，设计了一种Y形密封圈，并对密封圈的尺寸参数进行优化设计，这对轴承的密封具有积极意义。

通常密封圈的尺寸参数是利用经验设计得来的，而这很难使密封圈的各个尺寸参数达到最优值。而通过实验方法对密封圈进行优化，成本是非常高的。目前对于密封圈的优化大多采用基于有限元的方法，通过正交试验获得各个参数对密封性能的影响，进而对密封圈进行优化[2-5]，而这种方法的试验次数少，需要设计安排试验。而使用有限元方法进行密封研究，充分利用了计算机技术，能够使效率更高，结果更精确。BELFORTE等[6]利用有限元技术，对气动执行机构活塞的弹性体密封截面进行了优化；ACHENBACH[7]利用计算机仿真技术对密封圈在不同环境下的寿命进行了预测；谌彪等人[8]利用有限元软件对Y形密封圈在不同工作压力下的变形和受力情况进行了有限元分析。本文作者利用基于有限元的概率设计系统获得各个参数对密封性能的影响，利用基于APDL的ANSYS有限元优化技术对密封圈进行优化。

1 模型的建立及有限元分析

1.1 有限元分析模型

文中研究的旋转尾管悬挂器轴承为一种推力圆锥滚子轴承，其结构如图1所示。该轴承通过2个Y形密封圈进行密封。文中主要研究该轴承的外密封特性。首先对其外密封结构进行简化。考虑到轴承整体的轴对称性以及所受载荷的轴对称性，将三维的密封结构转化为轴对称的二维模型进行分析研究。简化后的模型如图2所示。

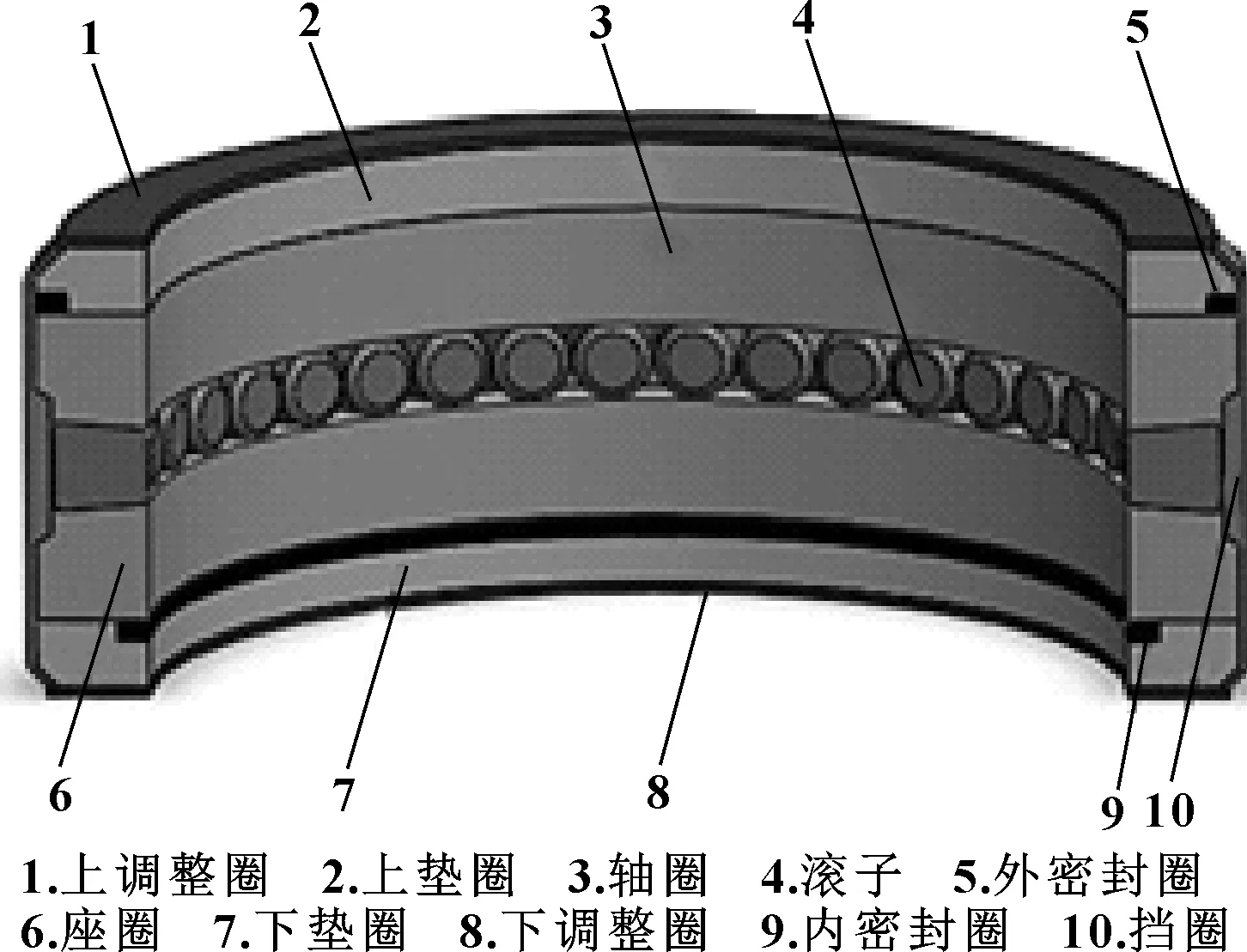
图1 旋转尾管悬挂器轴承[9]

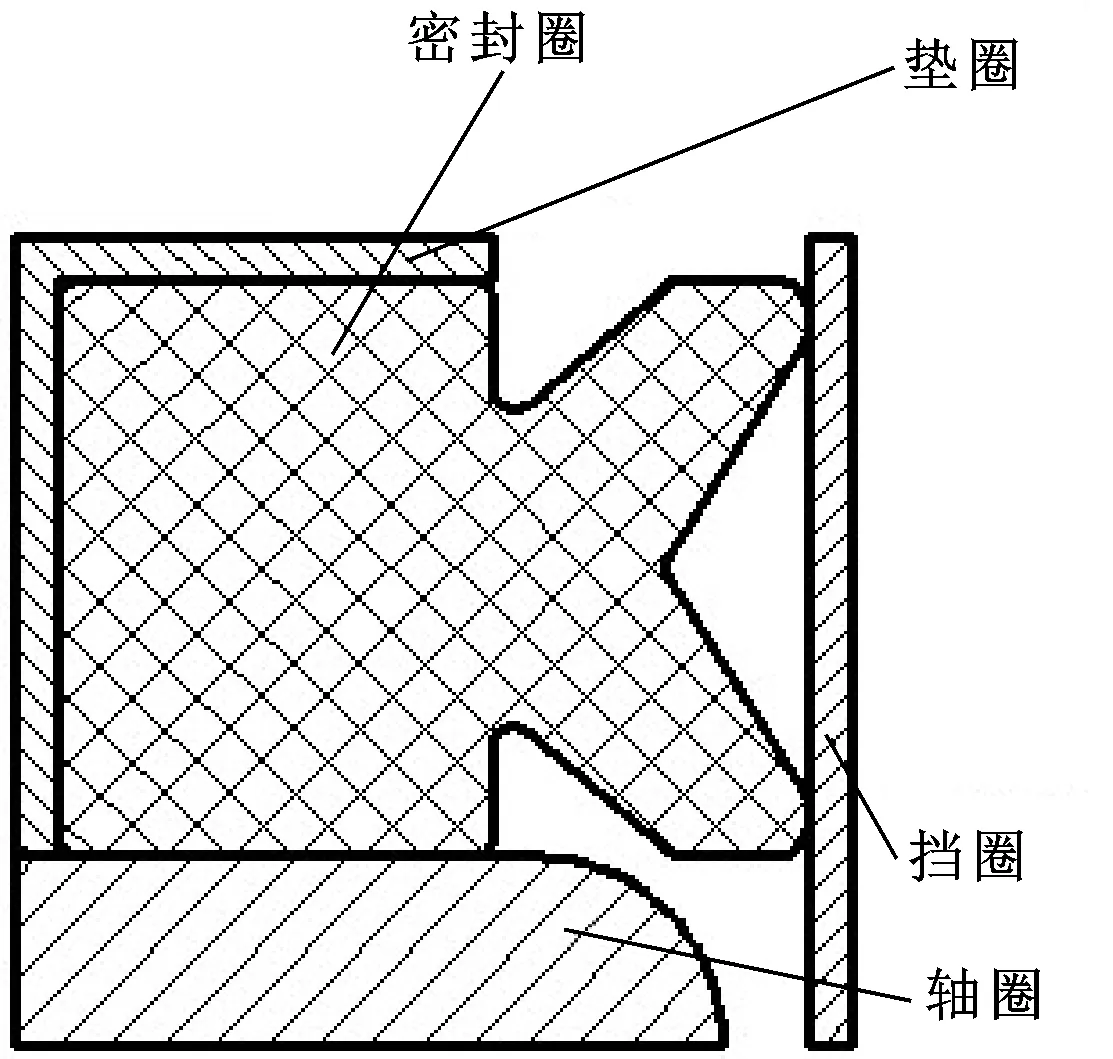
图2 简化模型

1.2 材料属性及单元类型

Y形密封圈材料为氟橡胶，密度为1.82 g/cm3，泊松比取0.49[10]，其邵尔A硬度为70±5或80±5(HG/T 2811—1996),在此取85。橡胶材料选择Mooney-Rivlin模型，其常数C01、C10的关系以及弹性模量E与邵尔A硬度(用HSA表示)[11-13]为

(1)

因此，Y形密封圈弹性模量取13.23 MPa，材料常数C10取1.764 MPa，C01取0.441 MPa。在定义材料属性时对其弹性模量、泊松比、密度、材料常数C01、C10进行设置。

Y形密封圈采用二维4节点的Plane182轴对称单元。Plane182单元具有求解塑性、超弹性、蠕变、大变形、大应变等问题的能力。而不作为主要求解对象的挡圈、垫圈、轴圈在实际分析过程中简化为线。

1.3 接触对设置

在密封结构中密封圈分别与轴圈、上垫圈、挡圈接触。因此，创建3个接触对即可充分模拟密封结构中的接触情况。且这3个接触对均为刚体/柔体的接触，接触方式为面-面接触。通过接触对设置向导创建接触对时，将刚性表面设置为目标面，即轴圈、上垫圈、挡圈与密封圈接触的面，将柔性体表面设置为接触面，即密封圈与轴圈、上垫圈、挡圈接触的面，使目标面的外法线方向指向接触面。接触对之间的摩擦因数为0.2。

1.4 载荷及边界条件

文中主要考虑静态下Y形密封圈在装配时的轴向过盈量和径向过盈量，工作时的工作介质压力对密封性能的影响，如图3所示。因此，限制垫圈在X方向上的位移，在Y方向上施加-0.1 mm的位移，即轴向过盈量。对轴圈施加固定约束，限制挡圈在Y方向上的位移，在X方向上施加-0.2 mm的位移，即径向过盈量。施加工作压力为6 MPa。

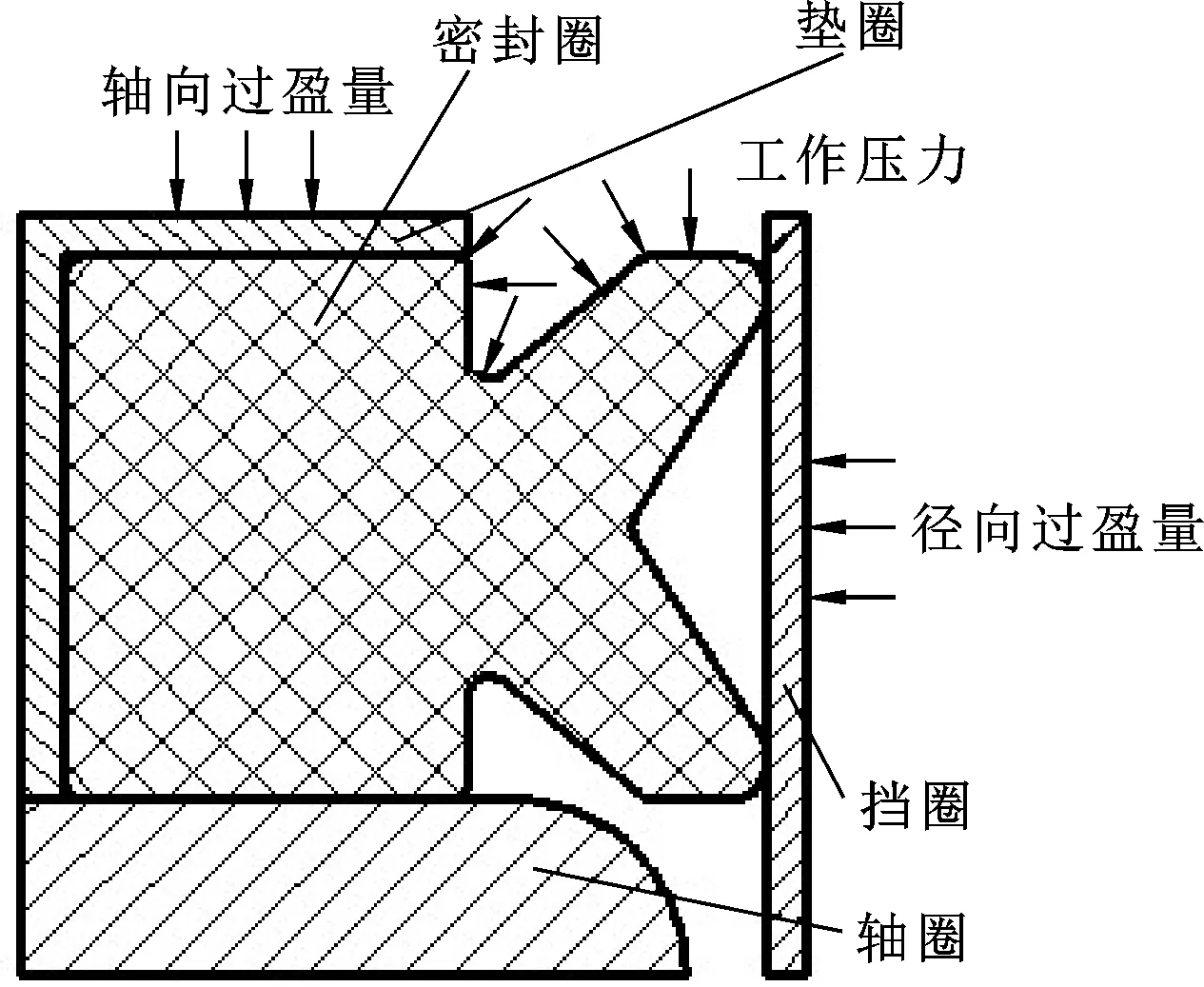
图3 密封圈过盈量及工作压力分布

1.5 有限元分析结果

将分析类型设置为静态分析,激活大变形效应和时间步自动阶跃选项进行求解。密封圈的接触应力云图如图4所示,von Mises应力云图如图5所示。从图4可看出，最大接触应力出现在根部，大小为12.96 MPa，大于其工作压力，可以实现密封;下密封唇与轴圈接触处以及密封唇与挡圈接触处也有较大的接触应力，且接触应力越大密封效果越好。从图5可以看出，Y形密封圈的最大von Mises应力出现在上密封唇根部，大小为20.74 MPa，密封圈在工作时此处最易造成断裂。因此，需要对最大接触压力及最大von Mises应力进行优化以达到更好的密封效果。

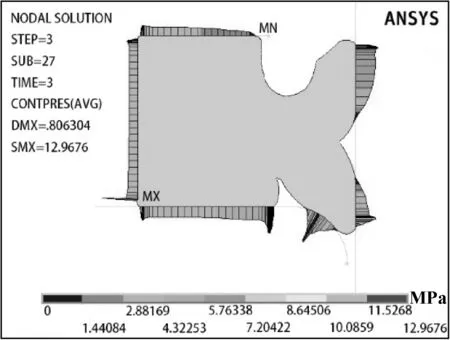
图4 接触应力云图

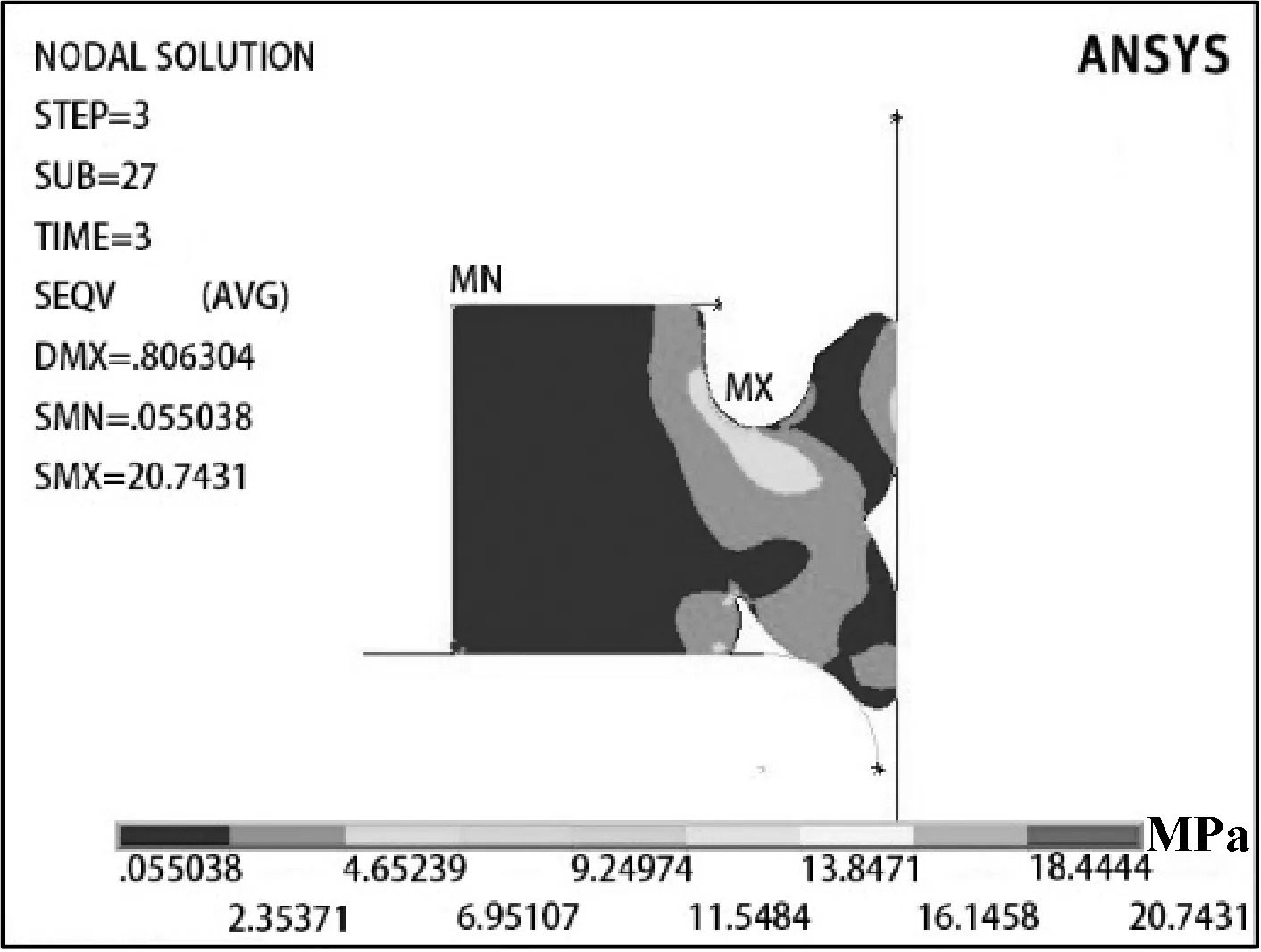
图5 von Mises应力云图

2 密封圈的灵敏度分析

因Y形圈的截面复杂，在生产过程中会造成几何尺寸的偏差，影响着其性能以及密封性。因此，对密封圈进行灵敏度分析有着重要意义[14]。

ANSYS提供的基于有限元的概率设计系统(PDS)的主要应用方向之一是：确定在所有不确定性的输入参数中哪个参数的不确定性对响应参数的影响程度最大，或者说对于目标产品最容易引起其工作失效，响应参数对输入参数变化的灵敏度有多大。

文中应用PDS模块分析了密封圈的几何尺寸对最大接触应力和最大等效应力的影响，得到最大接触应力和最大等效应力对输入参数(几何尺寸)变化的灵敏度，从而得到对最大接触应力和最大等效应力影响最大的主要尺寸，为后续的优化设计提供支持。

2.1 建立分析文件

PDS处理器利用分析文件复制创建概率设计的仿真循环文件，然后执行一系列概率设计分析循环。分析文件就是基于APDL的参数化有限元分析过程。

通过对旋转尾管悬挂器轴承的密封结构有限元分析的命令流进行提取，然后对提取的命令流进行了编写和加工，得到参数化的有限元分析过程文件。

2.2 定义输入、响应参数

将密封圈的几何参数定义为输入参数，假设其均服从高斯正态分布。定义的输入参数如表1所示，表中输入参数对应的尺寸如图6所示。

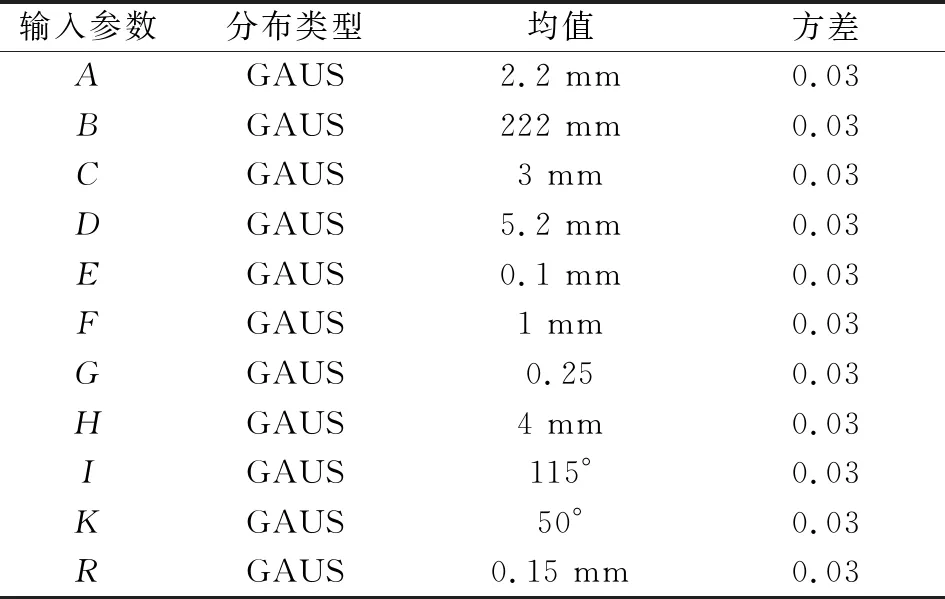
表1 定义的输入参数

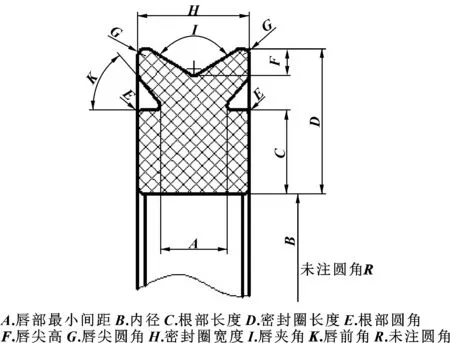
图6 密封圈的几何尺寸

将密封圈变形产生的最大接触应力和最大等效应力作为输出变量，并从有限元分析的结果中提取出来。定义的响应参数如表2所示。

表2 定义的响应参数

2.3 概率设计的结果

采用蒙特卡罗模拟技术中的拉丁超立方抽样法进行概率设计，该方法具有抽样“记忆”功能。设置抽样次数为600次。

图7所示为响应参数JCMAX2对输入参数变化的灵敏度。可以看出，影响JCMAX2的输入参数有I、H、D、C，灵敏度大小依次为I>H>D>C，其中I和响应参数为负相关，输入参数A、B、E、F、G、K以及R对响应参数JCMAX2没有影响。

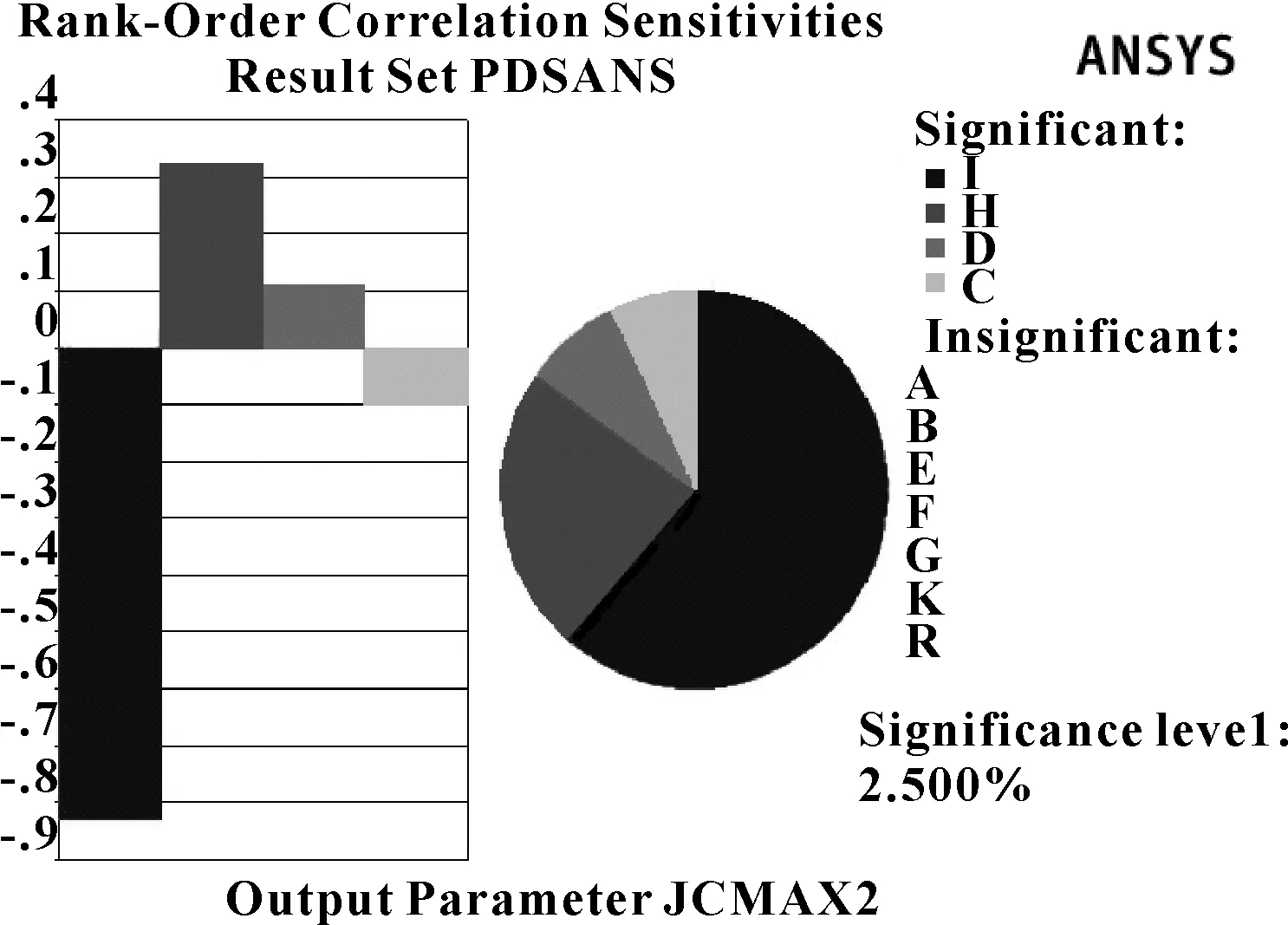
图7 响应参数JCMAX2对输入参数变化的灵敏度

图8所示为响应参数DXMAX对输入参数变化的灵敏度。可以看出，影响DXMAX的输入参数有D、H、I、C、A、F，灵敏度大小依次为D>H>I>C>A>F，其中D、I、A和响应参数为负相关，输入参数B、E、G、K以及R对响应参数DXMAX没有影响。

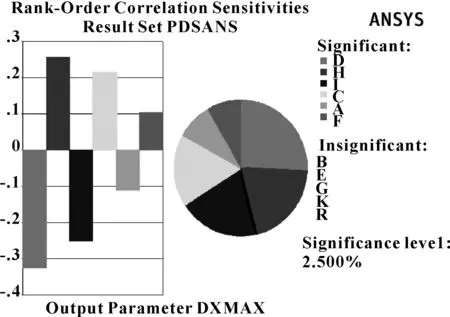
图8 响应参数DXMAX对输入参数变化的灵敏度

因此，影响响应参数JCMAX2和DXMAX的共同参数有I、H、D、C，即唇夹角、密封圈宽度、密封圈长度、根部长度。在后续优化设计中将对这4个几何尺寸进行优化。

3 密封圈的优化设计

ANSYS基于有限元分析的优化设计技术可以在满足设计要求的条件下搜索最优设计方案。

3.1 优化目标

密封圈若要适应于工作状态，则应该满足2个条件，即：密封圈与挡圈接触的最大接触应力要大于工作压力；密封圈的最大等效应力要小于额定等效应力。密封圈与挡圈的最大接触应力的大小不应比工作压力大太多，否则密封圈会产生较大的摩擦力，从而导致唇口磨损严重，同时产生较大的摩擦热。最大等效应力对密封圈来说则是越小越可靠。

因此，密封圈的优化目标为：密封圈与挡圈的最大接触应力不小于工作压力，密封圈的最大等效应力要小于额定等效应力，且越小越好。

3.2 定义变量

在用ANSYS进行优化设计时，首先要确定分析文件，优化分析文件除了包括参数化的有限元分析过程，还需要在文件中指定设计变量、状态变量及目标函数。

对灵敏度分析中得到的影响密封圈与挡圈最大接触应力和最大等效应力的4个几何参数I、H、D、C进行优化，从而增大密封圈的最大接触应力，降低最大等效应力。将4个参数定义为设计变量，并指定其约束范围。其约束范围从灵敏度分析的样本均值趋势图得到。定义设计变量的命令流如下：

OPVAR,C,DV,2.8,3.2

OPVAR,D,DV,4.9,5.5

OPVAR,H,DV,3.8,4.2

OPVAR,I,DV,110,117

将密封圈与挡圈的最大接触应力定义为状态变量，其命令流如下：

OPVAR,JCMAX2,SV,6,12

目标函数是要尽量减小最大等效应力的数值。在此将最大等效应力DXMAX定义为目标函数，其命令流如下：

OPVAR,DXMAX,OBJ

3.3 优化分析结果

ANSYS支持零阶优化和一阶优化2种方法，文中使用零阶方法进行优化[15]，设置最大循环次数为100次，执行优化分析后列出优化序列，其命令流如下：

OPSAVE,OPTZ,opt

OPTYPE,SUBP

OPSUBP,100

OPEXE

OPLIST,ALL

表3给出了分析得到的优化序列，可以看出，共产生了8个(SET 1至SET 8)设计序列，其中给出最优的是SET 8。

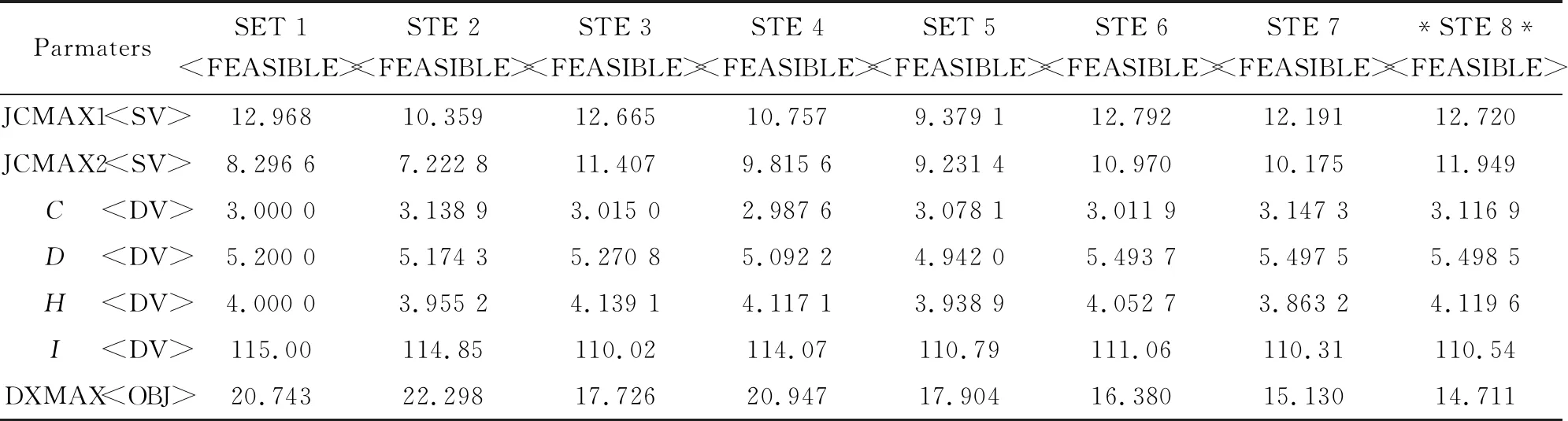
表3 优化序列

优化结果如表4所示。

表4 优化结果

优化前后密封圈的二维截面图如图9所示。由优化后的参数计算得出的密封圈有限元分析结果如图10、11所示。最大接触应力JCMAX2为11.949 MPa，大于其工作压力，且比优化前的8.296 6 MPa增大了44%。最大等效应力DXMAX为14.711 MPa比优化前的20.743 MPa降低了29.1%。因此，优化后使得密封圈拥有更好的密封效果，并且可延长密封圈的使用寿命。

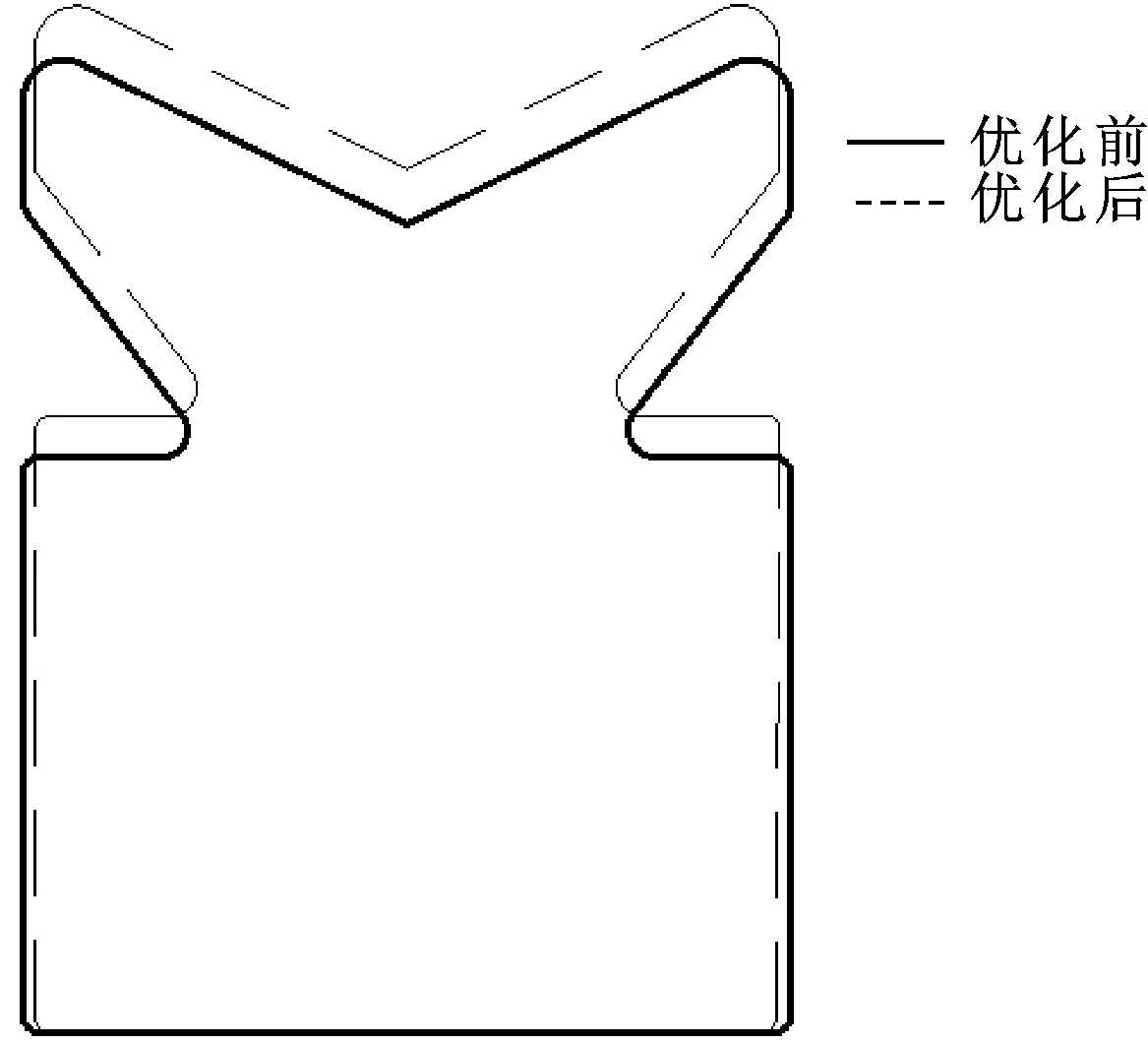
图9 优化前后密封圈的二维截面

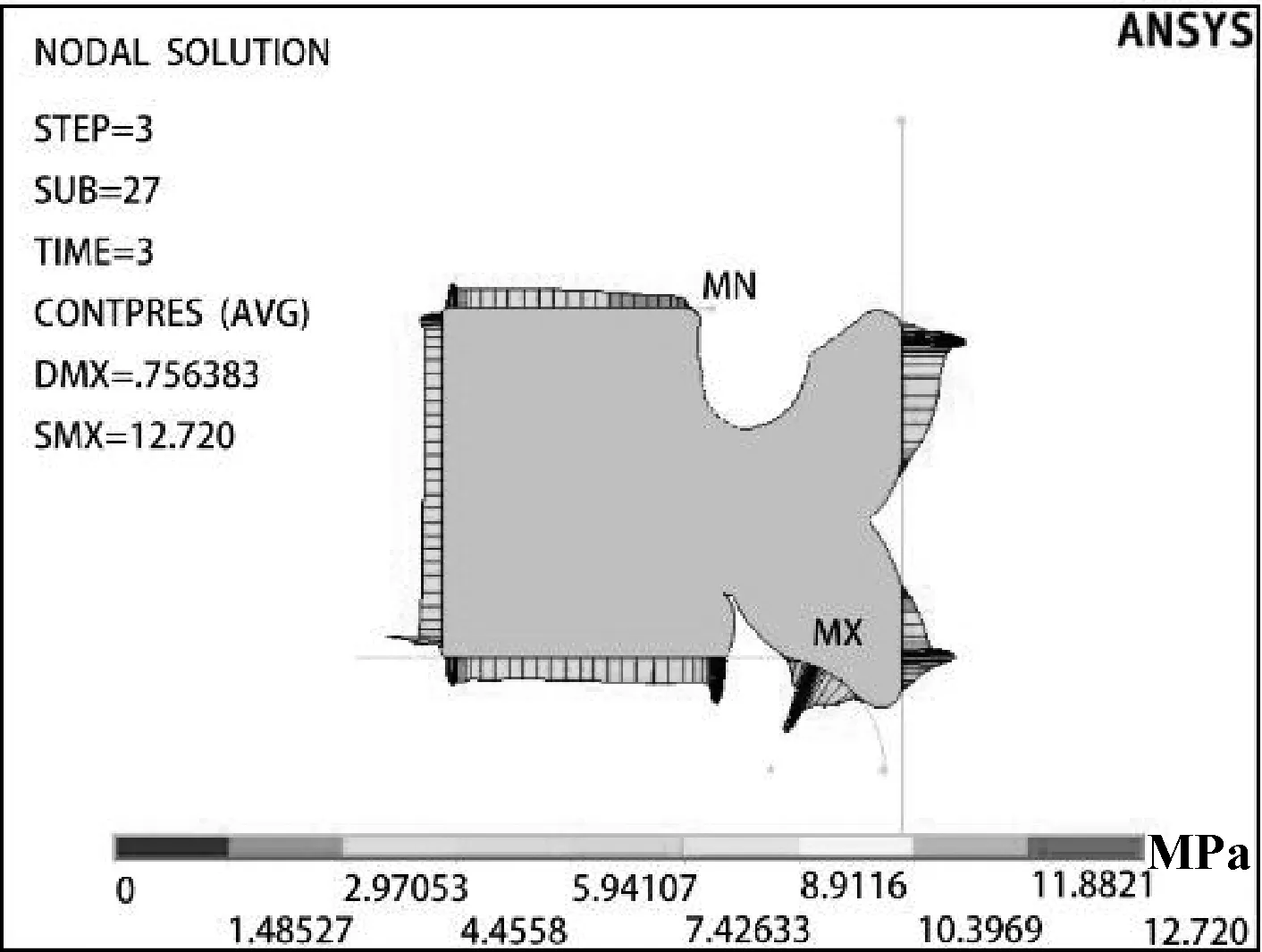
图10 优化后接触应力云图

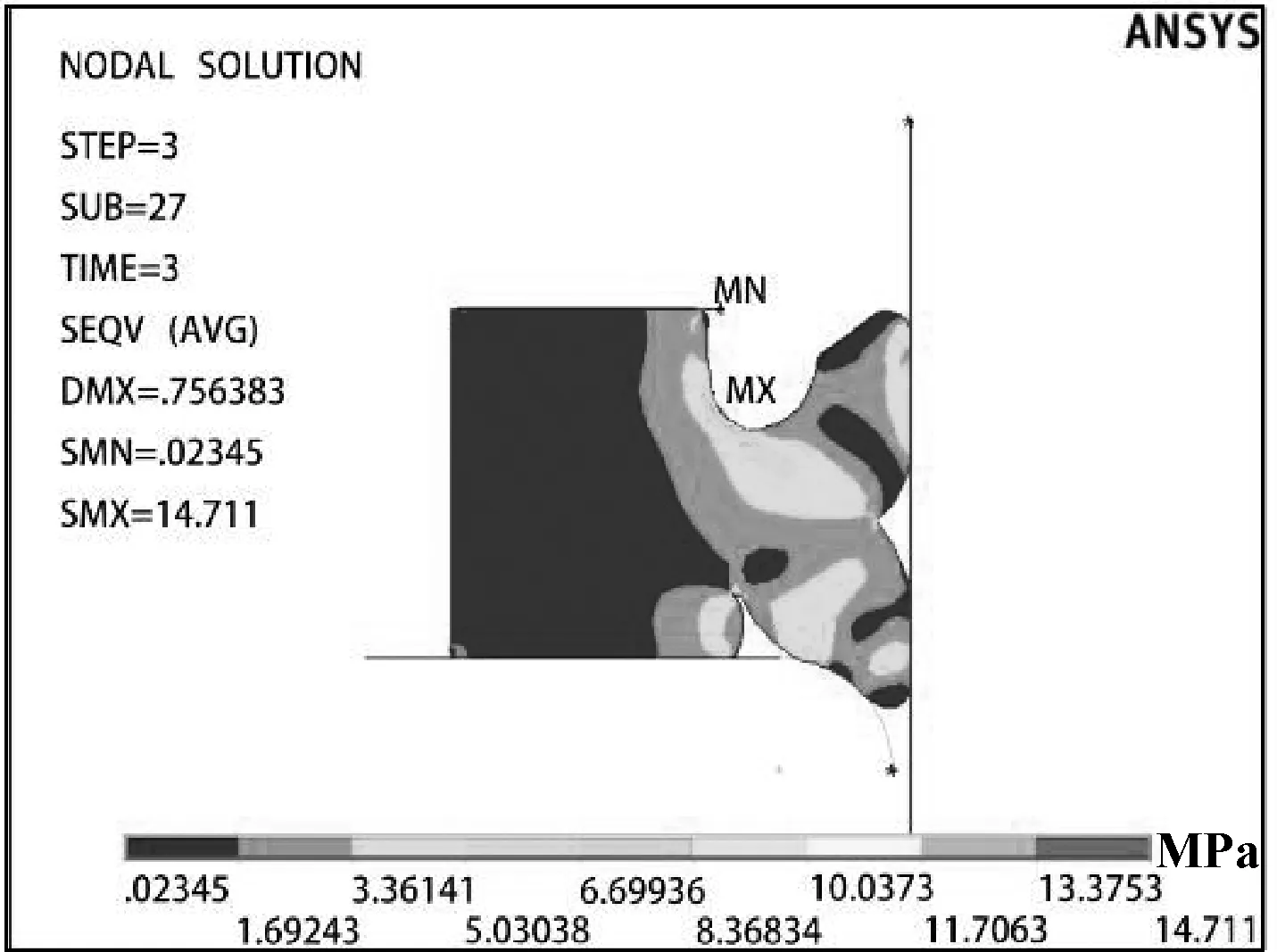
图11 优化后von Mises应力云图

4 结论

(1)设计的Y形密封圈在工作时，下密封唇与轴圈接触处以及密封唇与挡圈接触处有较大的接触应力；最大等效应力出现在上密封唇根部，工作时此处最易造成断裂。

(2)灵敏度分析表明，影响密封圈与挡圈最大接触应力的结构参数有I、H、D、C，灵敏度大小依次为I>H>D>C，其中I和最大接触应力为负相关，结构参数A、B、E、F、G、K以及R对最大接触应力没有影响；影响最大等效应力的结构参数有D、H、I、C、A、F，灵敏度大小依次为D>H>I>C>A>F，其中D、I、A和最大等效应力为负相关，结构参数B、E、G、K以及R对最大等效应力没有影响。

(3)对影响密封圈最大接触应力和最大等效应力的4个几何参数I、H、D、C(即唇夹角、密封圈宽度、密封圈长度、根部长度)进行优化设计，优化结果为：根部长度为3.116 9 mm，密封圈长度为5.498 5 mm，密封圈宽度为4.119 6 mm，唇夹角为110.54°。优化后密封圈与挡圈的最大接触应力增大了44%，最大等效应力降低了29.1%。