水基拉延油混合体系黏度的广义预测模型*

赵子锐 王承学

(长春工业大学化学工程学院 吉林长春 130012)

拉延油作为一种加工用油，在冲压钢的生产过程中起着非常重要的作用,其性能关系到冲压产品的质量、生产效率、后期加工乃至加工的成功率[1]。常用的拉延油具有冷却、清洁的作用，并具有润滑、防锈、抗极压、抗氧化、抗起泡等特点[2]。目前市场上拉延油产品大多是油基拉延油，存在无法水洗、易燃烧、对环境有污染、冷却不充分等缺点。为此，王承学和梁甜甜[3]研制了一种水基拉延油并已获得国家专利。与油基拉延油相比，水基拉延油具有黏度高、耐热性好、不发烫等优点，且加工后不需要使用洗涤剂清洗，对环境友好。

黏度是水基拉延油的一个重要物理参数[4-10]，影响到拉延油的涂布、清洗、润滑等使用性能[11]。不同的冲压钢生产方式需要不同的产品黏度来配合，因此需要建立模型来控制黏度。

目前，有许多经验公式和半经验公式可用于预测混合物黏度，这些公式大多来源于实验数据的回归分析[12-14]。Arrhenius模型是最典型的以混合比为基础计算混合体系黏度的模型，它适用于计算纯烃混合物的黏度[14]。BINGHAM提出了一种基于理想溶液的混合液体黏度计算新模型，KENDALL-MONROE提出了一个估算烃类混合物黏度的模型，CRAGOE提出了对数组分黏度倒数与质量分数乘积的线性组合模型，用于计算高黏度混合物[15-16]。

黏度与物料类型、配比、温度有关[1]。水基拉伸油同时具有牛顿流体和非牛顿流体的性质[1]，随着温度的升高，体系由混合型向牛顿型转变。因此，在环境温度随季节变化明显的情况下，需要改变水基拉伸油的混合比例，以适应不同的工艺和操作环境。此外，用一种黏度模型来计算黏度也是比较困难的，因此有必要建立一个包含可调值的黏度模型。

为获得一种最适合的水基拉延油混合体系黏度预测模型，本文作者在不同温度下对不同配比的水基拉延油样品的黏度进行了测定，采用几种黏度模型对水基拉延油的黏度进行预测，提出一种适用于水基拉延油等含牛顿流体和非牛顿流体混合体系的黏度预测模型。

1 水基拉延油的流变性能分析

为配制合适黏度的水基拉延油，将温度和各组分的比例视作可调节变量。以一种由水(A)、盐(B)和酯(C)组成的水基拉延油为例，调整三者的比例，制备10种水基拉延油试样，在恒温水浴和机械搅拌下，使用旋转黏度计(NDJ-1，12 r/min)测量试样在不同温度下的黏度。根据环境温度和材料的凝固点，实验设定在20～60 ℃温度下测量试样黏度，温度间隔设定为5 ℃。试样中水与盐、酯的混合比例及测得的不同温度下的黏度如表1所示。

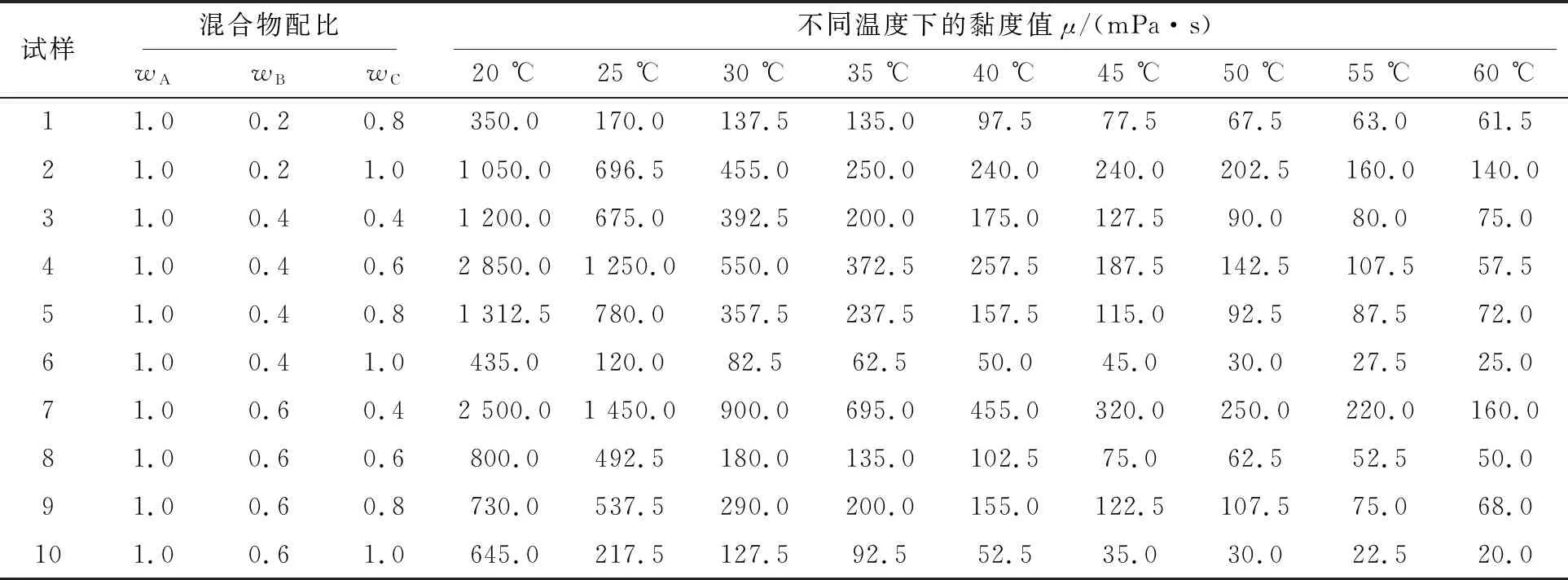
表1 水基拉延油的配比及在不同温度下的黏度测量结果

注：wA为水的质量分数；wB为盐的质量分数；wC为酯的质量分数。

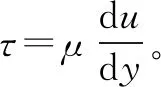
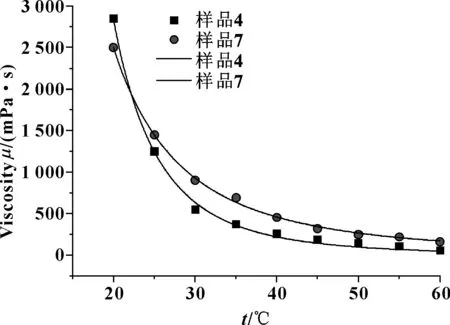
图1 样品黏度随温度的变化

2 水基拉延油黏度预测模型

2.1 常用黏度模型及预测分析

文中首先采用常用的Arrhenius模型、Bingham模型、Kendall-Monroe模型、Cragoe模型对水基拉延油的黏度进行预测分析。

(1)Arrhenius 模型

lnμ=φAlnμA+φBlnμB

(1)

(2)Bingham 模型

(2)

(3)Kendall-Monroe 模型

(3)

(4)Cragoe 模型

1/ln(2 000μ)=φA/ln(2 000μA)+φB/ln(2 000μB)

(4)

式中：φA为水的质量分数；φB为盐酯混合物溶液的质量分数；μ为拉延油黏度;μA为水的黏度;μB为盐酯混合物溶液的黏度；VA为水的体积分数；VB为盐酯混合物溶液的体积分数。

采用公式(1)—(4)计算不同配比的水基拉延油试样在给定温度下的黏度，并和实验数据进行比较。

图2所示为Arrhenius模型计算值与实验值的比较。可以看出，模型的计算黏度值小于实验值，且与实验值的差距较大，因此该模型不适合对水基拉延油体系进行黏度预测。

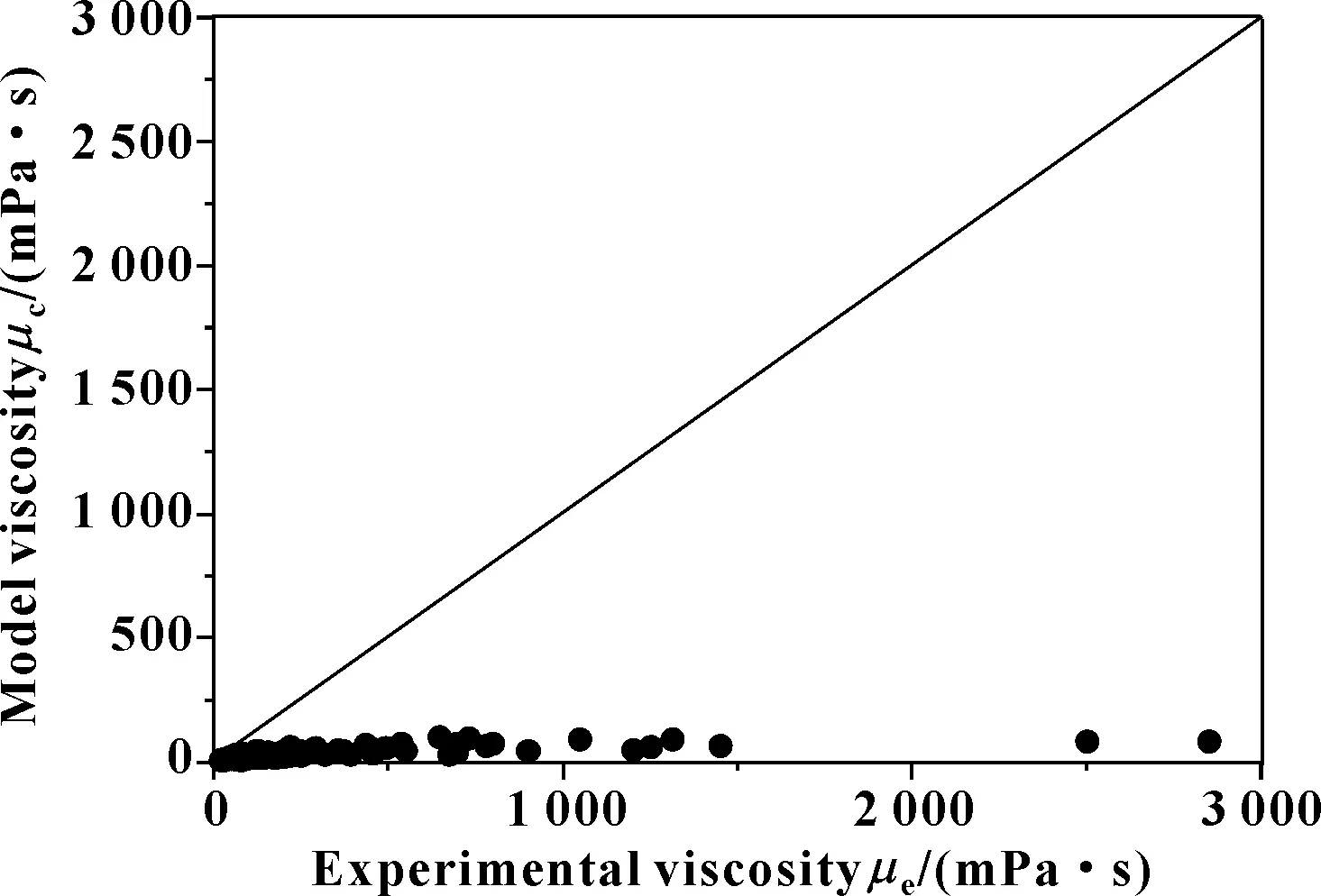
图2 Arrhenius模型计算结果与实验数据对比

图3和图4分别示出了Bingham模型和Cragoe模型的计算值与实验值的比较。可以看出，2种模型的计算值与实验值的差异比图2中的差异更明显，因此也不适合水基拉延油体系黏度的预测。

图5所示为Kendall-Monroe模型的计算值与实验值的比较。可以看出，与Arrhenius模型、Bingham模型和Cragoe模型相比，该模型的计算值接近于实验值，但在高黏度时的计算值与实验值差距较大，偏离实验黏度值拟合直线明显，因此该模型也不适用于水基拉延油体系黏度的预测。

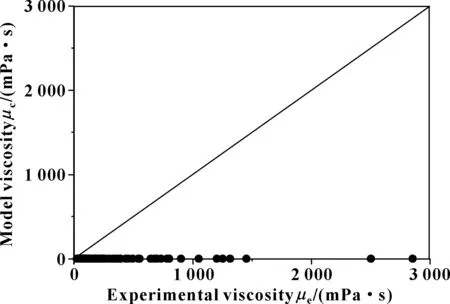
图3 Bingham模型计算结果与实验数据对比

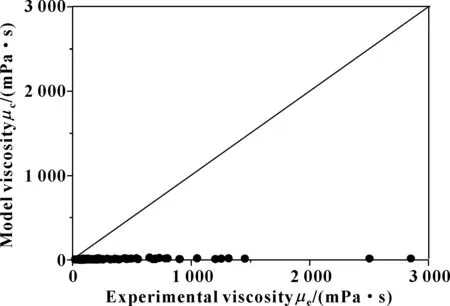
图4 Cragoe模型计算结果与实验数据对比

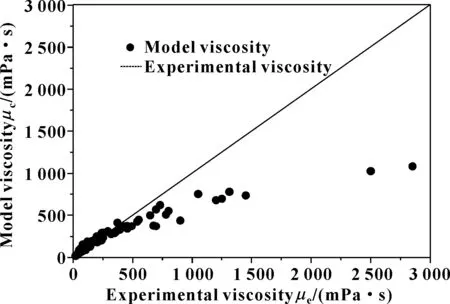
图5 Kendall-Monroe模型计算结果与实验数据对比

以上研究表明，常用的4种黏度模型均不能用于水基拉延油体系黏度的预测，需寻求一种新的黏度模型。

2.2 ASTM黏度模型及预测分析

由图1可见，水基拉延油混合体系的黏度随温度波动较大，需要采用一种可用于黏度波动较大的混合体系的黏度模型。GAO和LI[15]提出了采用ASTM双参数黏度方程来预测黏度，认为ASTM模型能很好地反映系统特性，对于黏度波动较大的混合体系有良好的预测效果。ASTM模型公式如下:

loglog(μ+0.7)=a+blogF

(5)

(6)

式中：t为温度(℃);a和b是系统的常数。

图6所示为ASTM模型计算值与实验值的比较。可以看出，模型计算值与实验值比较接近，且比较均匀分布在实验黏度值拟合直线两侧，因此该模型能够更好地对该体系进行模型预测。

但图6中该模型计算值小于实验值的数据较多。为分析ASTM模型的预测精度，分别用公式(7)和公式(8)计算拟合优度和平均绝对误差。

拟合优度公式:

(7)

平均绝对误差公式:

(8)

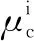
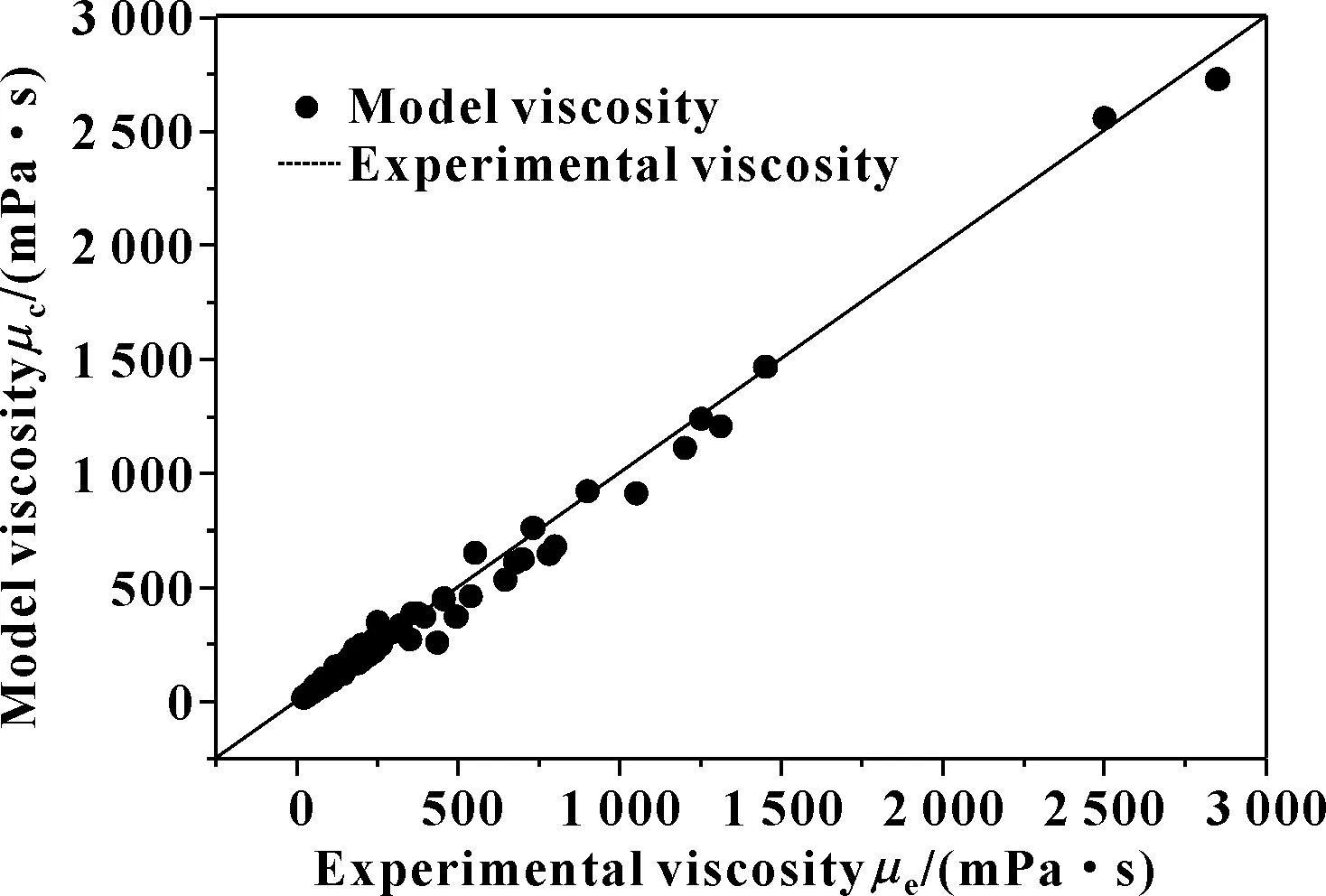
图6 ASTM模型与实验数据对比

表2给出了ASTM模型拟合10个样品黏度的拟合优度和a、b的值。模型的拟合度R2=0.989 8,平均绝对误差E=0.086 19，因此需要对该模型进行改进。

表2 ASTM模型拟合结果

2.3 ASTM模型的修正及预测分析

WALTHER提出了黏温公式，被ASTM推荐为黏温关系的标准。但是ASTM模型并没有直接包含混合比例。为了确定不同温度下的黏度数据，根据黏度要求，修正的ASTM模型计入了温度和混合比的影响。修改后的ASTM模型(M-ASTM)如下：

loglog(μf+0.7)=a+blogT

(9)

μ=μf(1-c·φB)d

(10)

式(9)(10)中a、b、c、d4个参数可以通过实验数据的回归分析得到。

图7所示为修正的ASTM模型的计算结果与实验数据的对比。利用公式(7)和公式(8)计算得到的拟合优度和平均绝对误差分别为0.990 7和0.047 5，这表明修正后的M-ASTM模型比ASTM模型预测得到的黏度数据更准确。

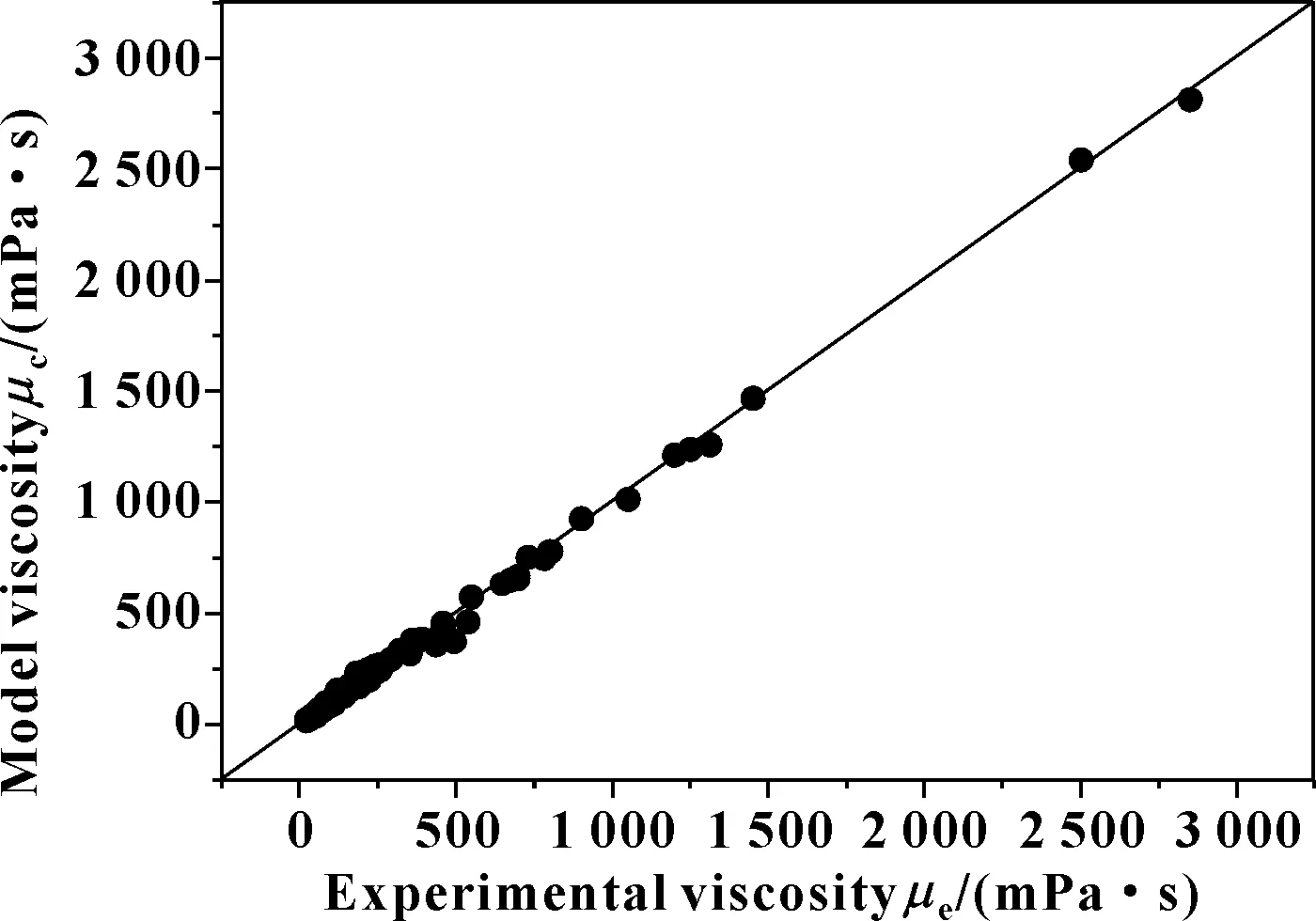
图7 修正的ASTM模型计算结果与实验数据对比

3 结论

(1)在20～45 ℃范围内，水基拉延油的黏度随温度变化明显，为非牛顿流体与牛顿流体的混合物；在50～60 ℃范围内，水基拉延油的黏度变化不明显，更接近牛顿流体。

(2)Bingham模型、Cragoe模型、Arrhenius模型和Kendall-Monroe模型的计算结果与实验数据有较大差异，不适用于水基拉延油黏度数据的预测。

(3)ASTM模型对黏度的预测优于其他模型，而修正后的M-ASTM模型预测效果更优，表明M-ASTM模型更适用于水基拉延油等含牛顿流体和非牛顿流体混合体系的黏度预测。