基础油中金刚石纳米颗粒润滑性能和导热性能的分子动力学分析*
冷岳峰 王嵩博 刘运宇 李 强
(辽宁工程技术大学机械工程学院 辽宁阜新 123000)
分子动力学(MD)模拟方法是研究热输运特性最有效的工具之一,特别是对于基于晶格动力学方法的复杂结构,其计算能力非常强大。LAMMPS是一种可对处于三态的粒子团进行建模的分子动力学代码,它可以使用各种原子间势和边界条件对原子、聚合物、金属、陶瓷、氧化物、颗粒或宏观系统进行建模[1]。
原子结构是影响金刚石、石墨烯、碳纳米管等重要的因素,利用原子间原子势的原子模拟方法是研究碳原子结构最有效的方法之一。但必须要有可靠的原子间势才能研究发现各种基本物理性质,如结构性质、表面特性、热特性等。现有的文献表明[2-3],纳米颗粒的含量、分散纳米颗粒的大小和形状、纳米流体的温度以及分散纳米颗粒的分布等因素都会影响纳米流体的热性能。这些因素中的每一个都是纳米流体传热现象广泛研究的来源,从而促进了该领域知识的发展。
纳米流体的概念最早是由DAI[4]在20世纪90年代中期提出的,作为一种替代微米级固体的方法,这些固体被用于传统的冷却剂中以提高其导热性。研究人员致力于进一步了解支配纳米流体的物理学,包括使用不同的方法计算各种类型纳米流体的热导率,以及研究热的机制。与传统流体相比,纳米流体具有更高的导热系数、更好的对流换热以及更低的压降,这使得纳米流体成为一种具有良好传热潜力的新技术。
SUKKAR等[5]将球形氧化铜纳米粒子和氧化钛粒子添加到润滑油中,研究了不同质量分数的纳米粒子在润滑油中的导热性,结果表明,纳米氧化铜颗粒对润滑油导热性能的提升优于氧化钛;当纳米粒子质量分数为0.1%时,含纳米氧化铜和氧化钛润滑油的导热系数分别增加了7.27%和4.54%。XIE等[6]研究了碳纳米管体积分数对纳米流体热导率的影响,发现碳纳米管使纳米流体导热系数提高了7%~20%。ASSAEL等[7]研究了在2种不同分散剂作用下碳纳米管水悬浮液的热导率,发现十六烷基三甲基溴化铵(CTAB)表面活性剂使得悬浮液导热系数增长了8%。HWANG等[8]研究了质量分数0.5%碳纳米管在矿物油基底液中的热导率,结果表明润滑油的热导率增加了9%。GARG等[9]采用超声波研究了碳纳米管对水基纳米流体传热性能的影响,发现质量分数1%碳纳米管可使水基纳米流体的导热系数提高20%。SINGH等[10]研究了碳纳米管对水-乙二醇纳米流体热导率的影响,发现质量分数0.4%的碳纳米管使得纳米流体热导率提高了72%。
李春风等[11]对富勒烯、石墨烯、金刚石、碳纳米管和纳米石墨的摩擦学性能进行了归纳总结,发现1%的富勒烯便可有效降低石蜡油摩擦因数33%;含5%富勒烯的石蜡油润滑下钢球磨斑直径可降低33%,摩擦因数降低了20%。ZHANG等[12]研究了棕榈油、大豆油、菜籽油分别作为MQL基础油的润滑性能,证明了3种植物油的润滑效果差异很小,摩擦因数只有0.04的差异,与液体石蜡相比都具有较低的摩擦因数。但是大豆油相比其他2种植物油,具有较低的黏度,更适合作为NMQL的基础油。
目前的文献都是针对一些水为基础液进行的分子动力学仿真,对基础油液加入金刚石纳米颗粒及其他碳结构的纳米颗粒研究较少。本文作者以蓖麻油酸为基础润滑剂,以金刚石纳米颗粒为添加剂,采用Tersoff势描述金刚石原子之间的势函数,进行了分子动力学仿真,研究了加入不同体积分数和不同粒径的纳米颗粒对润滑性能以及热导率的影响。
1 研究方法和数学模型
1.1 研究方法及理论基础
热传导是温度梯度引起能量传递的现象,属于非平衡过程。另一种计算热导率的方法就是基于非平衡分子动力学的模拟[13]。在该方法中,首先通过某种方式建立一个温度梯度,并等待足够长的时间,使得系统达到稳态。在达到稳态后,对系统的温度梯度和非平衡稳态热流进行测量,然后就可以根据傅里叶定律来计算热导率。
在此非平衡态研究热导率方法中,系统的总能量近似为
(1)
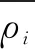
在参数优化的过程中,需要有正确的生成能和晶格常数。然而,仅用目前的方法很难得到具有正确晶格参数值的碳结构。此外,考虑到金刚石键合特性各不相同,试图用一种常见的势函数来描述内部原子的相互作用是不可取的。因此,有必要把金刚石和外部油液的相互作用分开,用不同的形式来描述它们。因此,最终决定用Tersoff形式描述金刚石原子之间的相互作用;用Lennard-Jones势来描述层间相互作用。根据Lennard-Jones作用势,原子间的相互作用[14]如下:
(2)
式中:εij表示力的强度的参数;σij表示原子大小的参数;r表示原子之间的距离。
基于文献[3,15]的研究结果,文中热导率的研究方法运用了速度重标法。当系统达到稳态之后,开始逐渐地增加热源中粒子的速率,并且对热源中的每一个粒子i,作如下速度转换
(3)
式中:vc是热源粒子的质心速度,
(4)
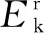
(5)
Δε是一个常数,该常数等于热源中能量的增量,
(6)
如果每 Δt作一次速度变换,则产生的热流密度大小为
(7)
其中,A是模拟系统在垂直于传导方向的横截面积。当使用周期性边界条件时,应当将该热流除以 2,因为当在某一位置注入热量时,热量将从热源区域两边流出,每一边流出的能量是总量的1/2。在系统达到平衡稳态之后,开始测量温度梯度,然后根据傅里叶定律计算非平衡态热导率。
1.2 物理模型和参数配置
图1给出了以蓖麻油酸为润滑剂的分子动力学模型,模型分为上下壁面,上壁面为金刚石,下壁面为金属镍,中间为蓖麻油酸分子以及内部的纳米金刚石颗粒。现以下壁面Ni原子层固定不动,上壁面的金刚石层以10 m/s的速度向右侧移动,同时对上壁面施加一个稳定的压力,以10 m/s的速度压缩,对摩擦过程进行模拟,用来模拟压缩和滑移时的过程。
在上下两层压缩面之间建立蓖麻油酸分子团尺寸为20 nm×10 nm×10 nm的基础流体,上下壁面为2 nm。金刚石纳米粒子的直径为4 nm,建立的模型总的原子数为22 584个。
模拟计算采用联合力场势函数,在x、y方向上采用周期性边界条件,在z方向上采用非周期性边界条件。在分子动力学模拟中,在有限温度下进行的实验中经常发现,金刚石结构在高温破坏或转变为其他结构之前应该是稳定的。

图1 低体积分数金刚石纳米颗粒润滑油的分子动力学模型
在具有周期性边界条件的直径4 nm的球形金刚石结构样品上进行了模拟。在模拟中,所有的性能计算都是在253 K左右温度下进行的。在253 K的条件下,经过300 ps时间步后,进行径向分布函数(RDF)的分析。在以前的研究中已经发现,如果一个结构不是稳定的,在几千个MD步骤内,原子结构很快会发生崩溃。因为布朗运动的作用,纳米粒子周围表现出较高的不稳定性,纳米粒子受到的布朗运动更加剧烈,对减摩性能有较大影响。
模拟过程中需要进行3个步骤:弛豫、压缩和剪切。首先进行弛豫,控制在253 K的温度下,采用联合力场,金刚石纳米粒子采用Tersoff势函数,镍单质采用EAM势函数,截断半径选取7.0,充分弛豫。施加压力,上壁面以10 m/s的速度压向下壁面。采用周期性的边界条件,模拟采用的计算方法为Verlet法,时间步长选定为0.1 fs。采用Nose-Hoover控温的方法,在NVT系统下对所有的原子进行弛豫,通过改变压力与温度以及纳米颗粒的粒径大小,文中重点考察不同条件下对薄膜润滑的原子分布、滑移特性和分子团聚特性的影响。
2 模拟验证及其讨论
2.1 数密度分析
当系统中存在固液气三态相交时,数密度可以很好地给出分界附近的结构性特点。粒子数密度的不均匀性导致粒子的输运也就是扩散现象。图2所示为中心壁面区域油膜厚度的原子数密度分布,可以发现近壁面区域的原子呈层状散布,这说明近壁面附近存在油膜吸附层。
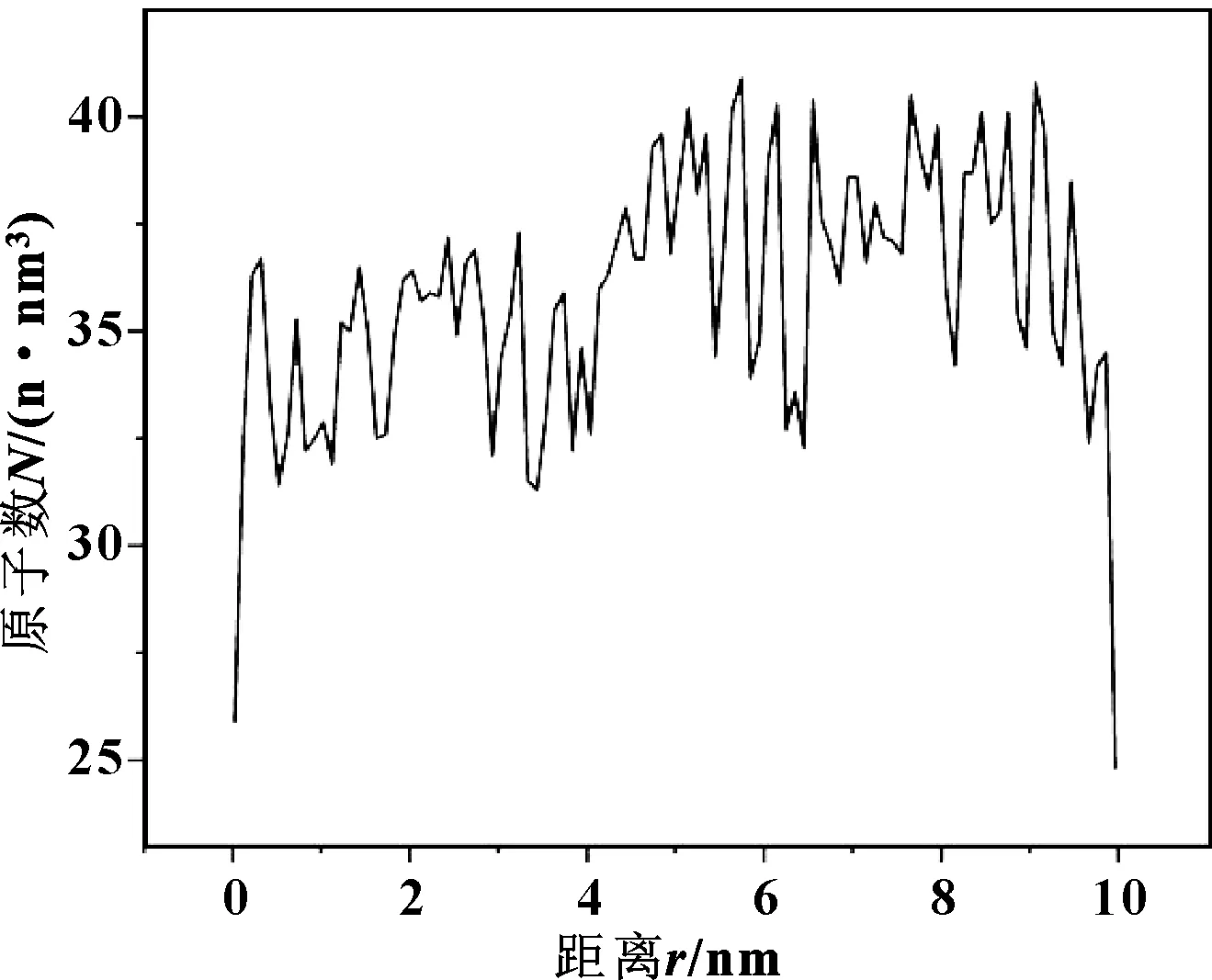
图2 中心壁面区域沿y轴的原子数密度分布
从图3中可以看出,金刚石颗粒周围存在吸附层,纳米粒子周围的密度较大,润滑剂附着在金刚石纳米颗粒上,当纳米颗粒被压扁时,这层薄膜也未被破坏。由此,可以认定金刚石颗粒周围的吸附层会对润滑剂分子产生影响,有可能会改变局部的密度等。另外,如果油膜相对比较厚,这种情况下的影响基本可以忽略,但对于比较薄的润滑膜,这种影响还是比较大的,不能忽视。
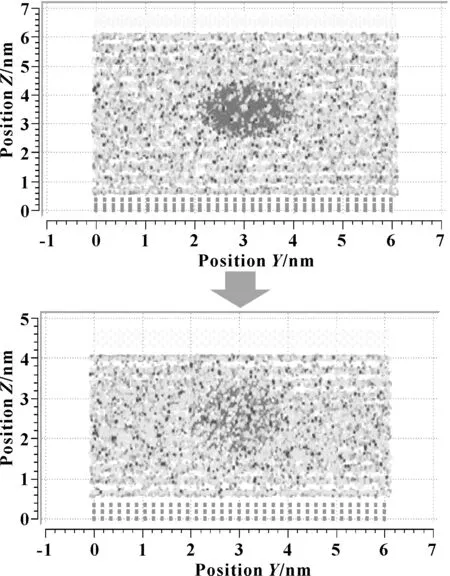
图3 压缩过程中纳米粒子的压扁状态和边界油膜吸附层
从图3中还可以看出,当位移在2 nm左右时,分子运动加快,大量的金刚石纳米颗粒周围分子被挤入前面吸附层。此时,金刚石纳米颗粒与壁面间存在一层润滑油分子。可以推测如果上下壁面进一步靠近,纳米颗粒将会与壁面直接接触,此时,薄膜就会发生破裂,从而就会发生固体润滑剂的作用。
2.2 径向分布函数分析
径向分布函数(RDF)是描述系统结构特点非常有效的方法,可以表征固体或液体微观结构的无序化程度[1]。图4所示为基础油蓖麻油酸的径向分布函数。
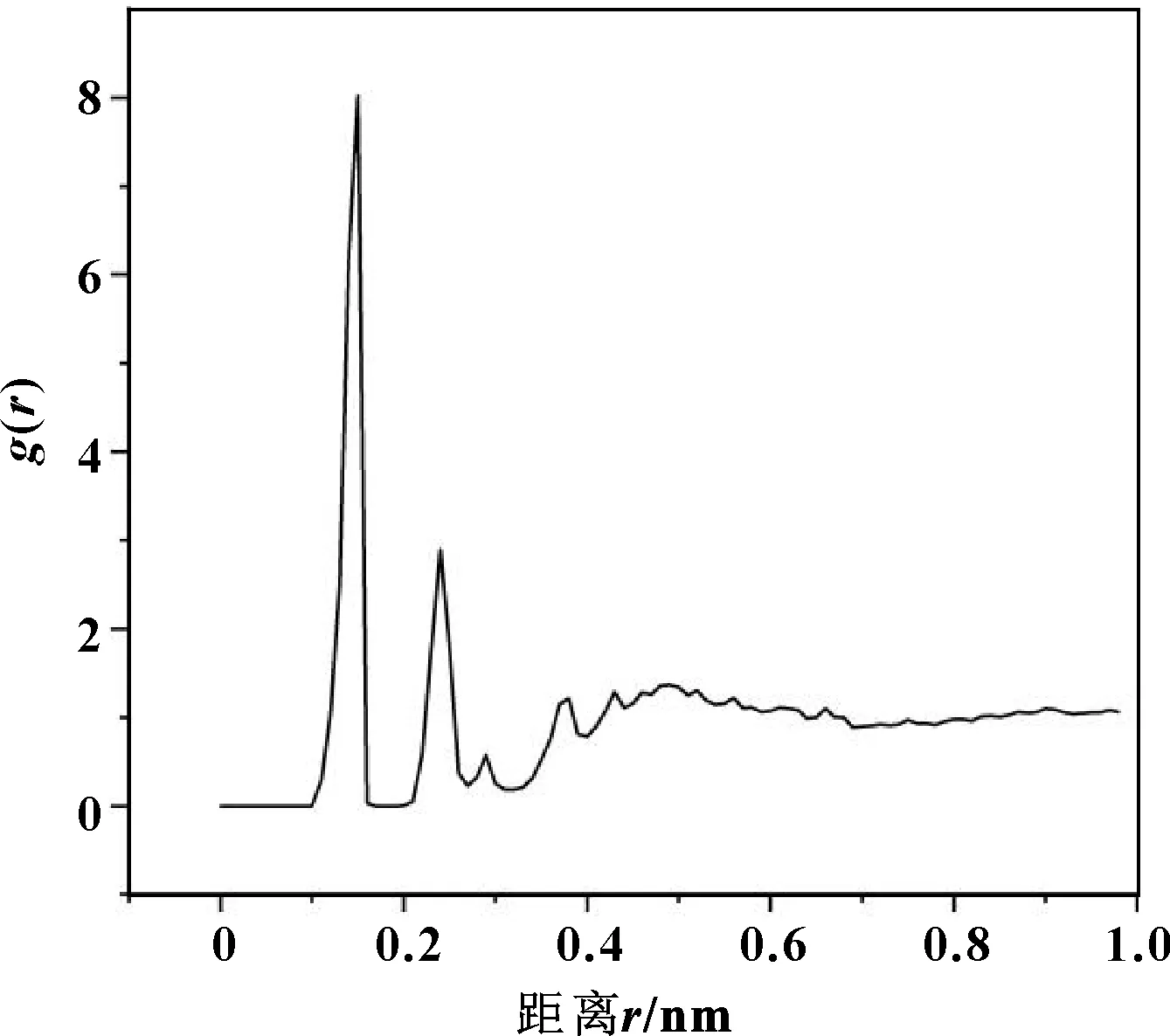
图4 基础油的径向分布函数(d=4 nm)
图5表示的是金刚石纳米润滑油分子团的RDF对比,可以发现纳米润滑油与蓖麻油酸基础油的RDF在2~4 nm之间有些许偏差,当上壁面位移超出这部分范围时,二者的曲线才逐渐趋于平稳,这说明金刚石纳米颗粒周围稀疏的吸附层对油膜分子排列的紧密程度和边界条件下润滑膜强度具有一定的影响,但是影响不大。
当油膜的厚度下降到某一程度后,油膜的各部位厚度就会发生转变,转变为“上下壁面吸附层和四周吸附层以及金刚石纳米颗粒”,三者之间的彼此作用提高了边界润滑膜的强度和承载力。可以看到纳米粒子并没有明显的变形,只是随着油液一起向下运动,此时,油液分层现象更加明显,分层数也有一定的减少,单层油膜厚度也在增加,层数减小。但是,金刚石纳米颗粒只能在一定载荷范围内提高边界润滑的承载能力,载荷超过这一范围时边界膜将会发生破裂,导致边界润滑膜的承载能力失效。
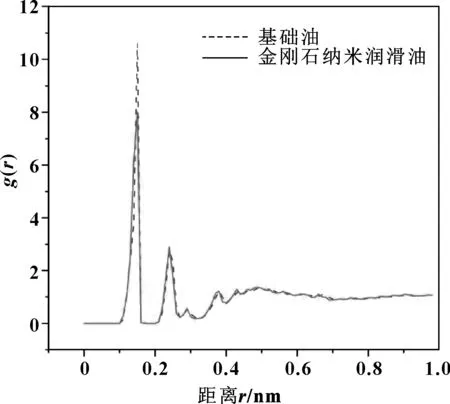
图5 金刚石纳米润滑油分子团与基础油液径向分布函数的对比(d=4 nm)
2.3 纳米颗粒的角速度分析
如图6 所示,改变周期性边界条件中的颗粒数量和粒径,使系统内的颗粒体积分数发生变化。当颗粒体积分数一定时,粒径变小,润滑膜承载力越高,金刚石颗粒的个数也会增加,纳米颗粒对基础润滑油的布朗运动效果也会加强,无规则运动也会进一步增强。

图6 高体积分数的纳米颗粒润滑油分子动力学模型
如图7—9所示,可以发现,粒径越小,纳米粒子的转动角速度越高,这个现象进一步说明了纳米粒子大小的扰动问题。此外,纳米粒子的直径扩大,增大了粒子体积效应的影响效果。因而,随着粒径的减小,纳米粒子润滑膜的承载能力增强,液固转化的压力变大,摩擦力降低。
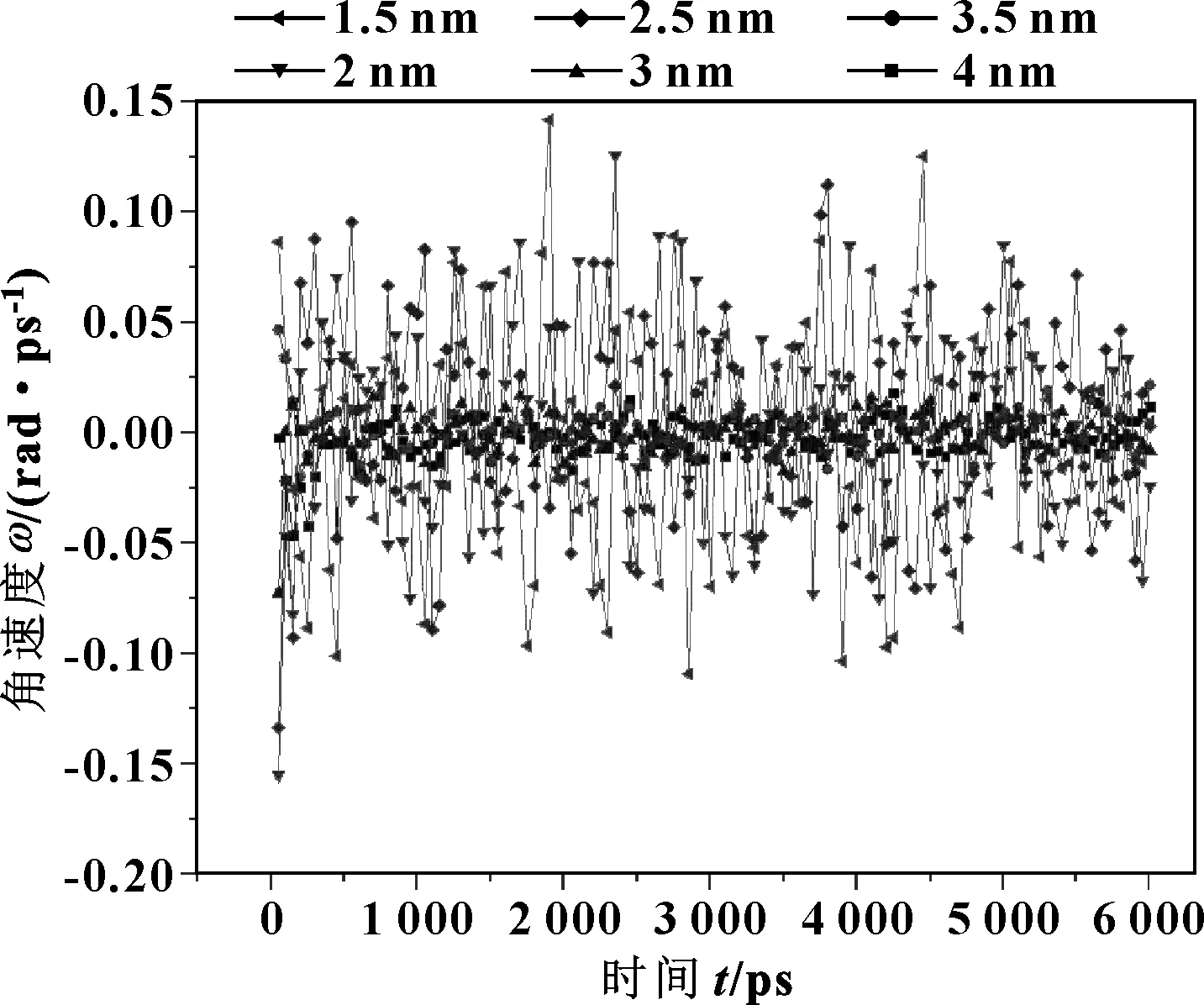
图7 不同粒径纳米颗粒绕x轴的转动角速度分量
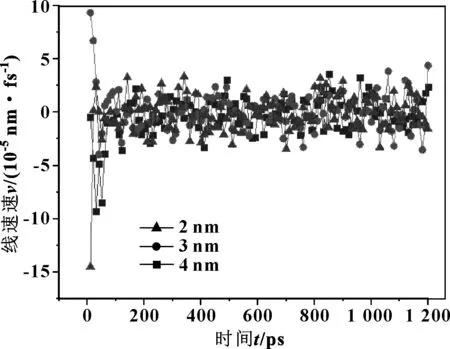
图8 纳米颗粒的线速度
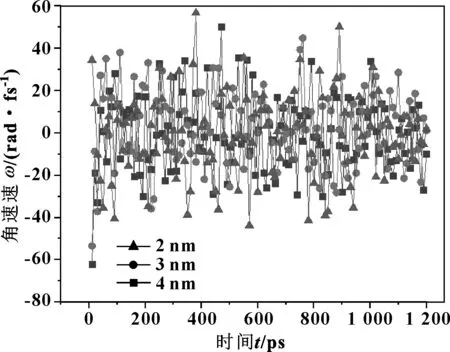
图9 纳米颗粒绕x轴的转动角速度
2.4 系统的热导率
根据热力学第二定律,一个系统在不受外力作用时,若其内部有热力学性质的不均匀性,则它一定处于非平衡的状态,并有向平衡态靠近的趋势。这种由热力学性质的不均匀性导致的热力学过程叫做输运过程。将一个系统置于2个温度不同的热源之间,最终会在系统内建立一个稳定的温度分布。可认为这样的系统处于一个稳态,但不处于一个平衡态。
如图10所示为非平衡态热传导模拟,在非平衡态热导率(NEMD)方法中,首先建立一个温度梯度,并弛豫足够长的时间,使得系统达到稳态。在达到稳态后,对系统的温度梯度和非平衡稳态热流进行测量,然后就可以根据傅里叶定律来计算热导率。将模拟系统在热传导方向分割为若干相等块,将其中的两块分别设置为热源区域和热汇区域。采用周期边界条件,块的个数一般取为偶数2N,并可以取第1块为热源,取第N+ 1块为热汇,或者反过来。
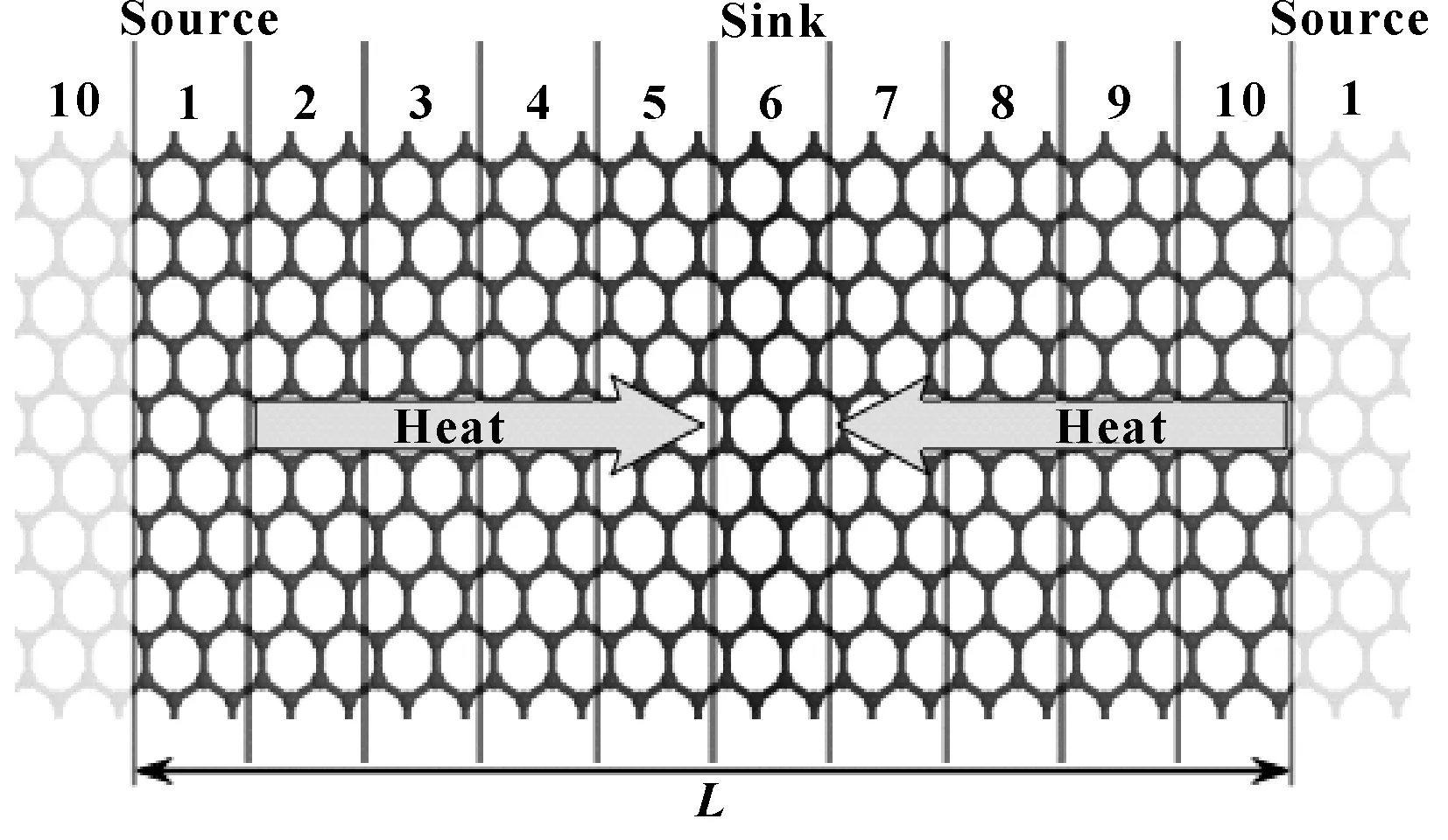
图10 非平衡态热传导模拟
在基础液油中,导热系数可以运用导热仪测得,如DTC-300,仅需比较小的样品,就可以通过比较小的容器测得,薄膜也可以使用多层技术准确得到测量值。但是在加入纳米金刚石颗粒之后,混合油模拟过程中的瞬时热导率只能通过计算机模拟得到。根据图11所示的体系温度分布,在体系的两侧添加热源并且绘制初始状态的温度分布情况。图12示出了模拟得到的热导率随模拟时间点的变化,热导率会在其准确值上下进行浮动,最后进行数据处理可以得到相对准确的数据。
图13所示是253 K温度下,纳米颗粒体积分数分别为0、0.6%、1.2%、1.8%和2.4%时润滑油的热导率。结果表明,纳米粒子体积分数的提高会极大地影响润滑油的热传导,使纳米流体的热导率呈近似线性增加。其主要原因是,纳米粒子的传热性大于液体分子,并且每一个加入的纳米粒子对液体都会有较大的扰动,从而增强了纳米流体的热导率。因此,在保证纳米流体液体性质的前提下,适当增大纳米粒子体积分数可以有效提高纳米流体的热导率。
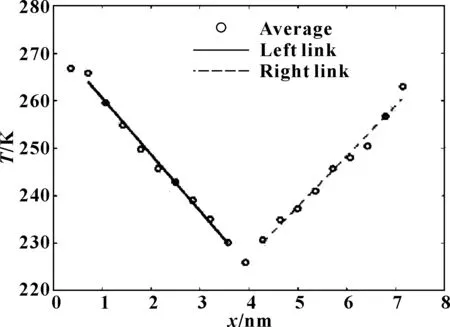
图11 系统局部温度热流
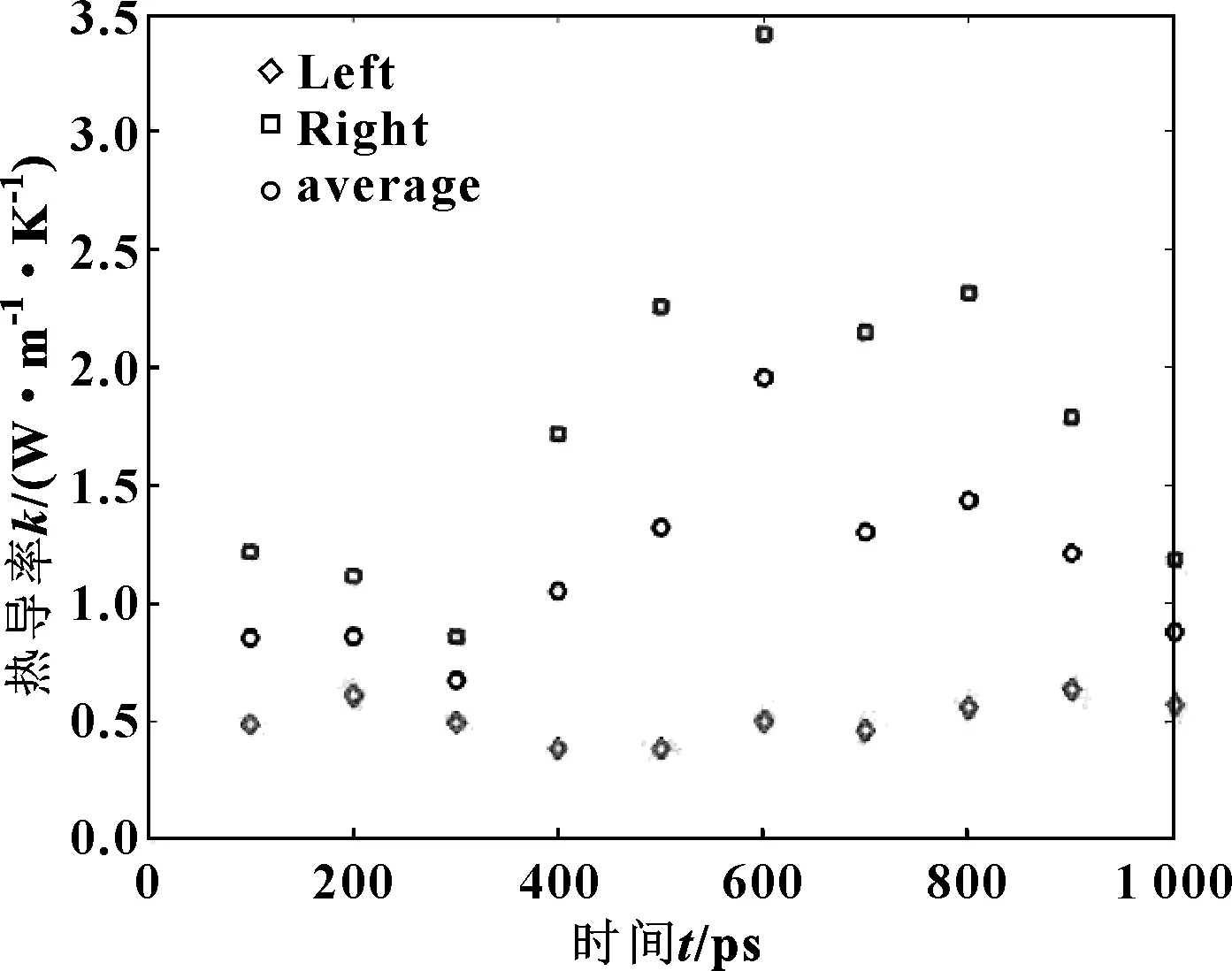
图12 热导率随模拟时间点的变化
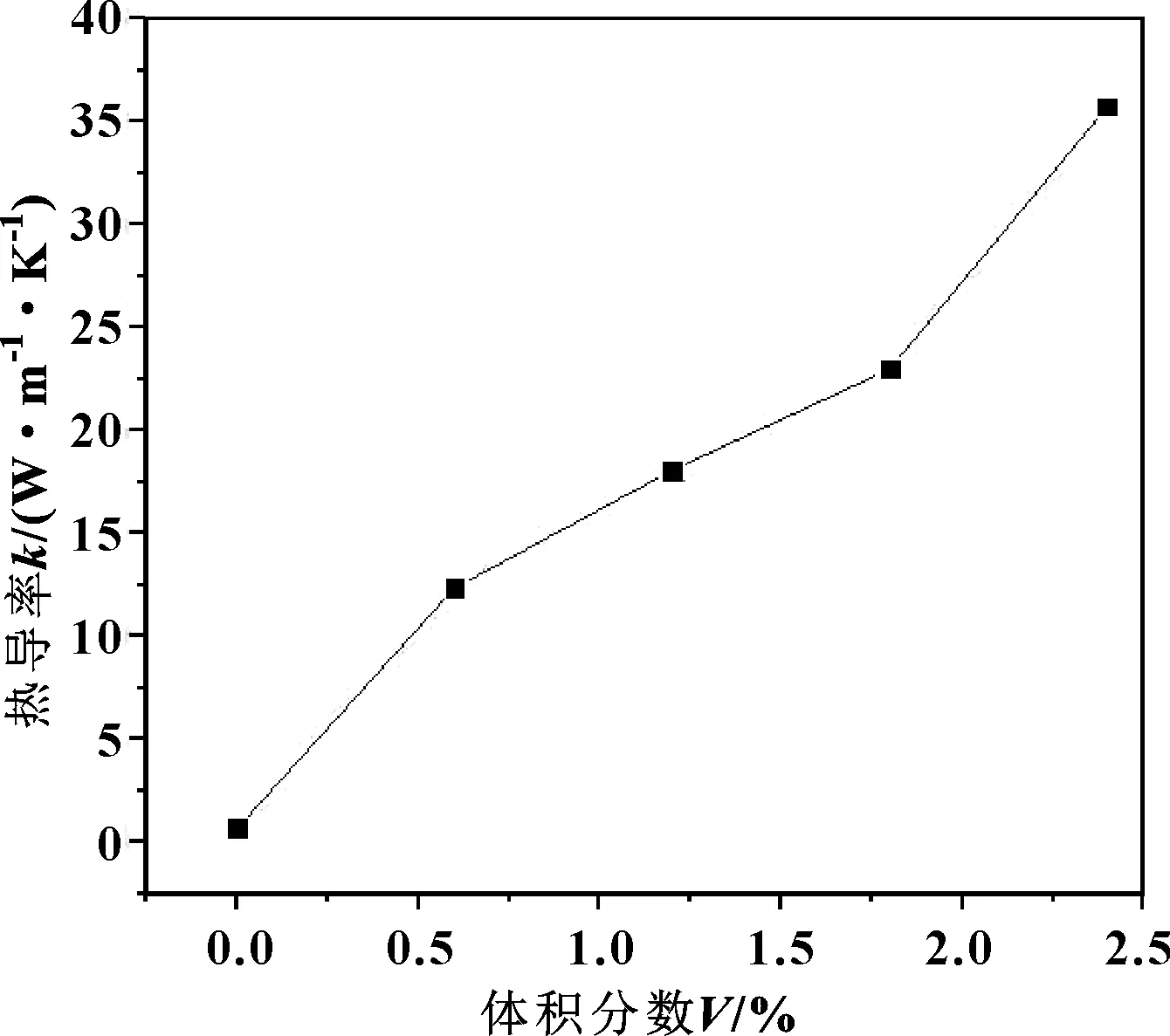
图13 不同体积分数纳米颗粒润滑油的热导率
3 结论
(1)纳米粒子加入基础油液中,会与基础油之间发生吸附作用,在纳米粒子表面形成吸附层,当载荷在纳米管润滑膜的可承受范围内时是可以存在边界润滑的。纳米粒子在布朗运动的作用下也会产生能量交换,促进纳米流体液体间的能量传递。因为布朗运动的作用,纳米粒子周围表现出较高的不稳定性。纳米流体与基础流体相比有更好的减摩性能,纳米粒子受到的布朗运动更加剧烈,对减摩性能有较大影响。
(2)在形成边界油膜后,金刚石纳米颗粒可以提高基础油液的承载能力,但是由于壁面和纳米颗粒周围的吸附层在压缩过程中不断靠近,纳米颗粒在边界油膜被破坏之前就发生了形变,在此之前,边界油膜能很好地保护纳米颗粒。
(3)当系统中的纳米颗粒粒径发生变化时,在压缩和滑动过程中,纳米颗粒的转动角速度会发生变化,粒径越小,转动速度就越高;反之,转动速度就越小,相应地摩擦力就会发生变化。
(4)利用非平衡态热导率的方法研究了纳米金刚石润滑油的热导率,发现纳米颗粒的加入会使得基础油液热导率提高,随纳米粒子体积分数的增加,纳米流体的热导率呈近似线性增加。
(5)文中研究方法也可用于其他系统的传热研究,在获得稳定的温度分布后,通过线性拟合的方法来确定温度梯度。所有的模拟都在热传输的线性响应范围内,进一步验证了傅里叶定律求得NEMD热导率方法的可行性。在模拟实验中可以发现,在比较长的样品模拟中,温度梯度应该很小,否则靠近热源的温度将偏离目标温度,导致温度分布非线性。

