高强不锈钢绞线网在ECC中的搭接性能

朱俊涛，赵奎，邹旭岩，王新玲，李可，张哲

(1.郑州大学 土木工程学院，郑州 450001；2. 郑州工程技术学院 土木工程学院，郑州 450044)

工程水泥基复合材料(Engineered Cementitious Composites，ECC)是一种新型的水泥基复合材料。与普通混凝土相比，由于纤维的桥联作用，使其具有拉伸应变硬化和多缝开裂的特点，提高了结构的延性和耗能能力[1]，但强度较低，需要结合增强材料来充分发挥其工作性能。普通钢筋强度低，难以充分发挥ECC的优异性能；纤维编织网性能优越，但经济性和施工性能较差[2-7]。而高强不锈钢绞线具有强度高、耐久性好及运输、施工方便等优点，常与环氧树脂或聚合物砂浆组合用于混凝土结构加固[8]。因此，基于两种材料(高强不锈钢绞线、ECC)的优点，提出高强不锈钢绞线网增强ECC这一新型复合材料[9-11]，既充分发挥了ECC和高强不锈钢绞线的优点，又克服了相应增强材料的缺点。

考虑实际工程施工，增强材料在基体中需要截断、搭接，而截断、搭接削弱了基体对增强材料的握裹作用，因此，需要对增强材料的搭接性能进行研究，以确保构件受力的安全性。学者们对增强材料在基体中的搭接性能开展了广泛研究[12-16]。Choi等[17]通过拉伸试验，研究了不同抗压强度的混杂纤维增强SHCC中搭接钢筋的粘结性能，并考虑搭接长度等多种因素影响，提出局部最大粘结应力和平均粘结应力计算公式。Metelli等[18]对纤维混凝土梁交错搭接钢筋进行试验研究，得出纤维掺量及截面搭接钢筋百分比对钢筋搭接性能的影响规律。方志等[19]研究了活性粉末混凝土中带肋钢筋搭接连接的受力性能，确定了活性粉末混凝土中纵筋的搭接长度。惠慧[20]通试验研究了不同因素(搭接长度、保护层厚度、混凝土强度、配箍率以及GFRP筋直径)对GFRP筋在混凝土中搭接性能的影响规律，提出了GFRP筋在混凝土中的搭接粘结强度计算公式及搭接长度计算公式。

综上所述，目前对各种筋材的搭接受力性能、破坏特点以及搭接长度等已有深入研究，中国现行规范也对搭接构造要求进行了相关规定。然而，对钢绞线网在ECC中搭接性能鲜有研究。因此，本文以横向钢绞线间距、相对搭接长度、钢绞线直径为试验参数，对39个搭接连接试件进行中心对拉试验，以探究高强不锈钢绞线网在ECC中的搭接连接性能影响规律，进而确定其临界搭接长度及相关构造措施。

1 试验方案设计

1.1 试件设计

共制作了39个拉拔试件，考虑不同试验工况分为4组，每组3个试件。试件设计图如图1所示。图中，a为试件长度，l0为非粘结段长度，la为搭接长度，c为试件的厚度。试件设计参数如表1所示。

图1 高强不锈钢绞线网增强ECC试件图(mm)Fig.1 Detail diagram of high-strength stainless steel strainer reinforced ECC specimen (mm)

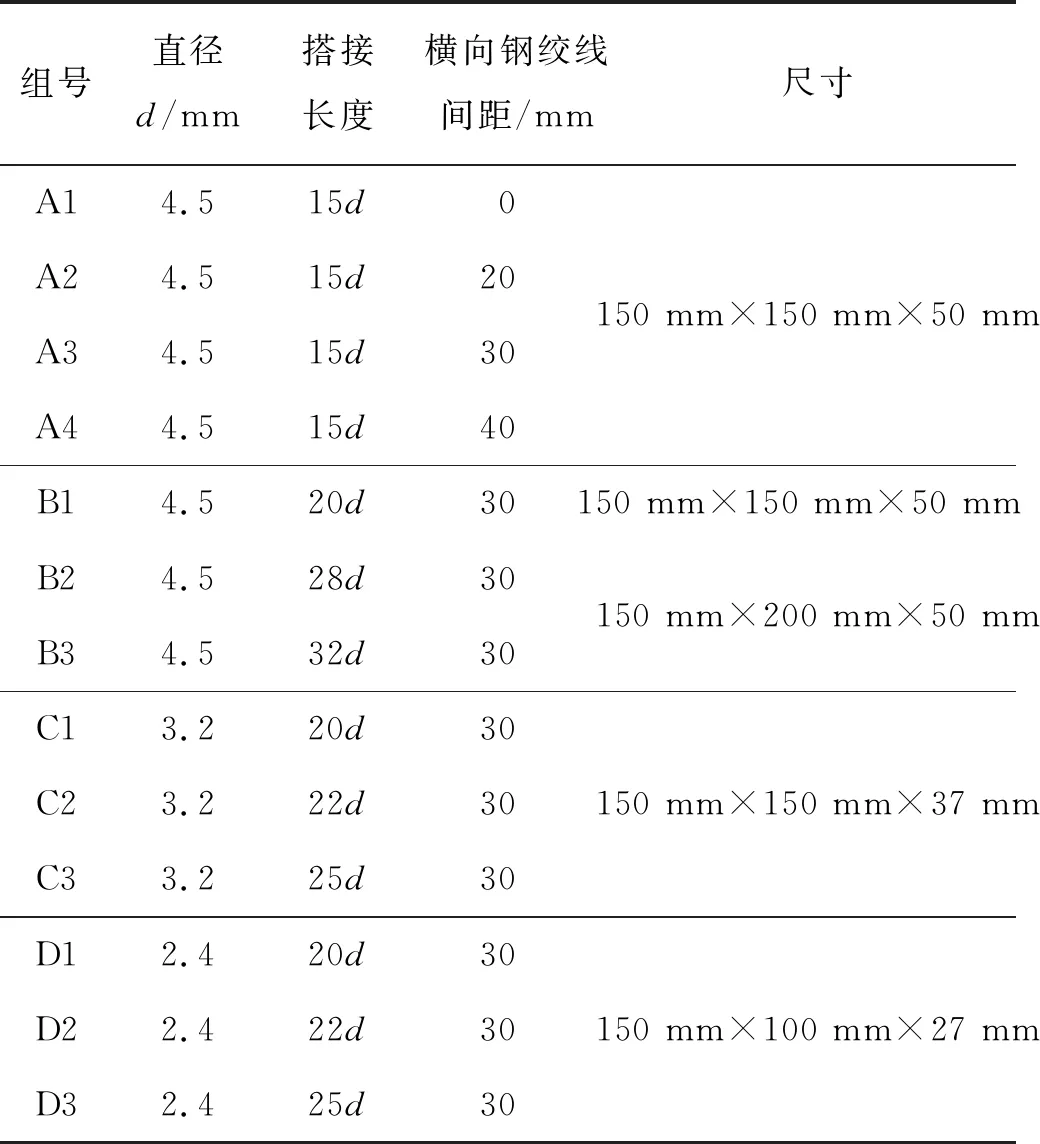
表1 试件参数Table 1 Parameters of ECC specimen

1.2 加载方式及量测方案

由于试验机尺寸限制，搭接试验在图2所示的自制钢吊篮中进行。试验采用穿心液压千斤顶进行手动加载，整个装置横卧式放置，左端为加载端，右端采用两块打孔的钢板对钢绞线端头进行固定。在试件上下两侧放置钢管保证试件处于装置中心位置，避免偏心受拉。

图2 试验装置及示意图Fig.2 Test equipment and schematic diagram

试验采用力加载方式，每级荷载按照5%的最大荷载进行递增。试验时，钢绞线被拉断或者拔出即停止加载。分别测量加载端B点和C点的相对位移。考虑AB、CD段受力较大且有一定长度，因此，B、C两点的实际位移可用A、D两点的位移分别去除AB、CD段的变形表示。

AB段变形:

(1)

式中：F为外荷载，即拉拔力；lAB为AB段的长度；ES、AS分别为钢绞线的弹性模量和实测截面面积。

从而可以得到试件左端的实际滑移Sl。

Sl=SA-SAB

(2)

式中：SA为A点的位移。

试件右端实际滑移Sr与左端滑移Sl计算方法相同。

粘结段的实际滑移量S：

S=Sl+Sr

(3)

平均粘结应力τ：

(4)

式中：d为钢绞线的公称直径；la为搭接长度。

1.3 材料性能试验结果

钢绞线：每种直径的钢绞线均取3个试样，其拉伸试验结果取平均值，见表2；其测得的应力-应变曲线如图3所示。

表2 钢绞线材料属性Table 2 Steel strand material properties

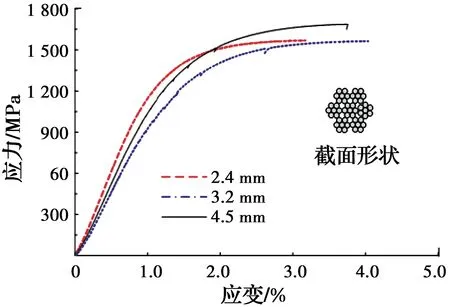
图3 钢绞线应力-应变试验曲线Fig.3 Stress-strain test curve of steel strand

ECC力学性能：ECC受压性能由70.7 mm×70.7 mm×70.7 mm立方体试块经28 d标准养护测得；其拉伸性能由薄板长条试件的单轴拉伸试验测得，试件尺寸为280 mm×40 mm×15 mm。ECC受拉应力-应变曲线如图4所示。其抗压强度、极限抗拉强度及对应的伸长率分别为32.45 MPa、2.83 MPa、2.2%。

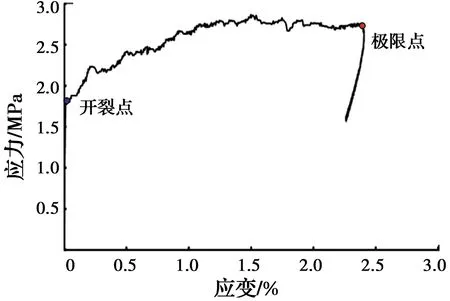
图4 ECC拉伸应力-应变试验曲线Fig.4 ECC tensile stress-strain test curve

2 试验现象及结果

2.1 试验现象

试验结果表明，钢绞线搭接的破坏模式分为两种：钢绞线拔出破坏和拉断破坏,其破坏模式如图5所示。

钢绞线拔出破坏(P)：A、B1、B2部分试件、C1、C2、D1、D2组试件钢绞线被拔出。从图6可以看出，试件加载初期，两端位移均缓慢增加，随着荷载增加，荷载-滑移曲线逐渐呈非线性，当接近峰值荷载时，荷载增速放缓，滑移增加较大，达到峰值荷载后，试件一侧纵向钢绞线突然被拔出约10 mm，同时，荷载降至峰值荷载的40%左右。

图5 试件破坏模式Fig.5 Failure mode of ECC specimens enhanced by high strength stainless steel stranding

图6 钢绞线破坏时的典型荷载-滑移曲线Fig.6 Typical load-slip curve when steel strand breaks

钢绞线拉断破坏(R)：B2剩余试件、B3、C3、D3组试件钢绞线被拉断。荷载-滑移曲线如图6所示，试件加载初期，两端位移均缓慢增加，随着荷载增加，荷载-滑移曲线逐渐呈非线性，当接近峰值荷载时，荷载增速放缓，滑移增加较大，达到峰值荷载前，滑移曲线非线性较为明显。随后，荷载达到钢绞线的极限承载力(4.5、3.2、2.4 mm钢绞线的极限承载力分别为14.4、7.8、4.3 kN)，整根钢绞线被拉断。

搭接试件发生上述破坏(钢绞线拔出、钢绞线拉断)时，荷载均迅速下降，破坏过程较为突然，脆性较大。此后，位移计所测数据产生较大偏差，因此，后续分析中仅考虑滑移曲线的上升段，不再考虑其下降段。

2.2 试验结果分析

表3为各试件的试验结果，从表中可以看出，A、B1、B2部分试件、C1、D1组试件(搭接长度较小)均为钢绞线拔出破坏。B2剩余试件、B3、C3、D3组试件(搭接长度较长)为钢绞线拉断破坏。A组试件(4.5 mm、搭接长度15d)峰值荷载基本接近，但A1组(无横向钢绞线)峰值荷载对应的滑移量为2.99 mm；A2-A4(横向钢绞线间距为20、30、40 mm)对应的滑移量分别为1.57、2.03、2.48 mm。由此可知，横向钢绞线的设置及间距的改变对钢绞线网/ECC搭接时的峰值荷载影响不大，但随着横向钢绞线间距的减小，各组试件峰值荷载对应的滑移逐渐较小。这表明横向钢绞线可以有效约束纵向钢绞线的滑移，并且随着横向钢绞线间距的减小，约束效果越明显，但未改变其脆性破坏的性质。B1-B3试件(搭接长度由20d增至32d)的峰值荷载由11.6 kN增至14.4 kN，对应的滑移量由2.21 mm增至2.77 mm；C、D组试件类似，表明钢绞线网的搭接长度对搭接性能影响较大。搭接长度均为20d的B1、C1、D1这3组试件(钢绞线网直径分别为4.5、3.2、2.4 mm)，随着钢绞线直径的增大，峰值荷载由3.84 kN增长11.60 kN，而对应的滑移量由2.38 mm降至2.21 mm，这表明钢绞线直径对其搭接性能影响较大。

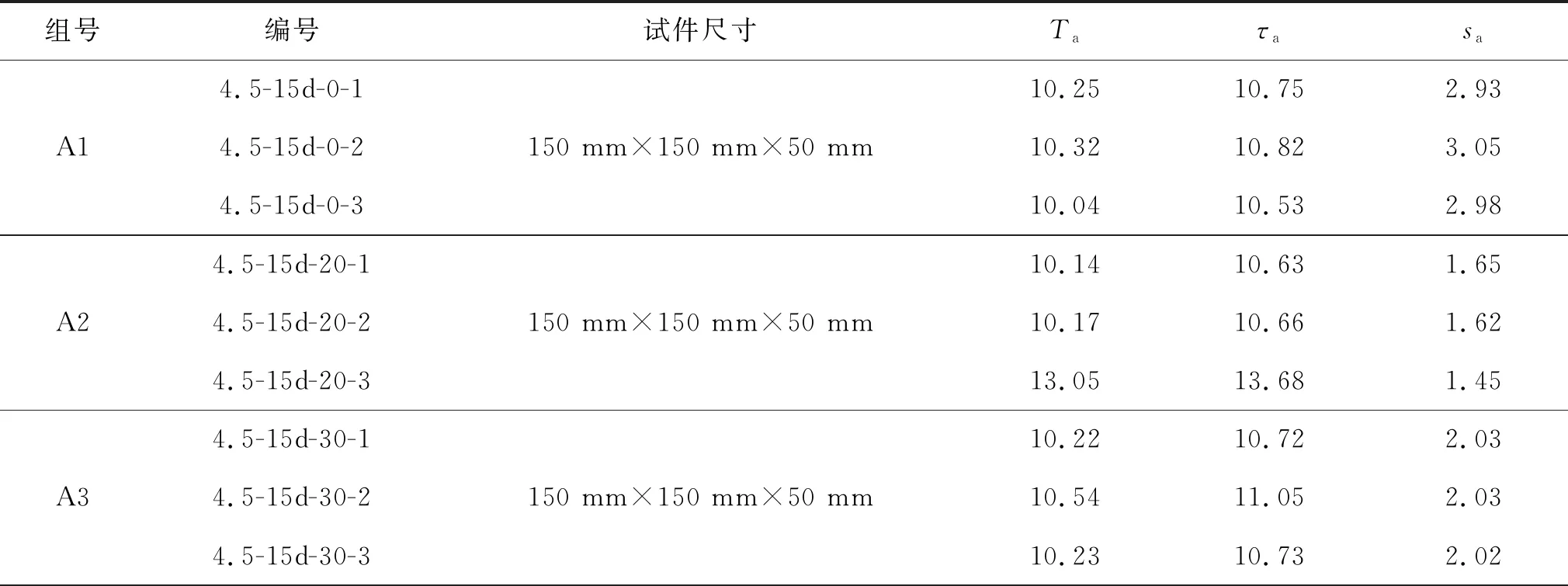
表3 试验结果Table 3 Test results

续表3

3 搭接性能影响因素分析

3.1 横向钢绞线及其间距影响分析

图7为A组试件(锚固长度为15d，A1无横向钢绞线，A2、A3、A4间距分别为20、30、40 mm)的荷载-滑移曲线。从图7中可以看出，A组试件的峰值荷载较为接近，这表明横向钢绞线的引入对搭接时的粘结力及搭接时的极限粘结应力影响不大。但达到峰值荷载时，对应的滑移量相差较大，且同级荷载下对应的纵向钢绞线滑移量随着横向钢绞线间距的减小而减小。

由试验结果绘制不同横向钢绞线间距(ld)与滑移量(sa)的关系曲线，如图8所示。从图8中可以看出，横向钢绞线的间距与峰值荷载对应的滑移量呈正相关；横向钢绞线间距越大，达到峰值荷载时的滑移量越大。这表明：对于搭接试件，横向钢绞线可以对纵向钢绞线形成有效约束，从而减小其相同载荷下的滑移量；且横向钢绞线间距越小，约束作用越明显。横向钢绞线的设置，对搭接试件的脆性破坏模式影响不大。该现象主要是由于搭接试件中两根纵向钢绞线并排放置，紧密靠拢，与粘结试件相比，钢绞线周围ECC的握裹作用减小，且两纵向钢绞线之间的ECC受到双向挤压，而横向钢绞线对其缓解作用有限。

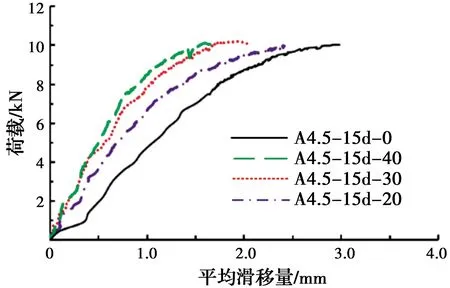
图7 不同横向钢绞线间距试件的荷载-滑移曲线Fig.7 Load-slip curve of specimens with different transverse steel wire spacing

图8 横向钢绞线间距(ld)与滑移量(sa)关系曲线Fig.8 Curve of relationship between transverse steel strand spacing (ld) and slip (sa)

3.2 搭接长度影响分析

由试验结果可知，搭接长度对钢绞线搭接连接性能影响较大，不同搭接长度试件的荷载-滑移曲线如图9所示。从图9(a)中可以看出，滑移初期，4.5 mm不同搭接长度的3组试件(搭接长度分别为15d、20d、28d)的滑移量相差不大；从图9(b)、(c)可以看出，3.2、2.4 mm不同搭接长度的3组试件(搭接长度为20d、22d和25d)，随着搭接长度的增加，同级荷载对应的滑移量减小。滑移后期，随着搭接长度的增加，相同荷载下产生的滑移量减小，但达到最大荷载时，滑移量变大。表明随着搭接长度的增加，“搭接刚度”增加。

图9 不同搭接长度试件的荷载-滑移曲线Fig.9 Load-slip curves of specimens were enhanced by different bond lengths

依据试验结果，绘制不同钢绞线直径试件相对搭接长度(la相对搭接长度是指钢绞线搭接长度与相应钢绞线直径的比值，为充分考虑并分析“搭接长度”单一因素对搭接性能的影响，采用相对搭接长度。)与滑移量(sa)的关系曲线，如图10所示。从图中可以看出，相对搭接长度与滑移量呈正相关，随着相对搭接长度的增加，达到峰值荷载时的滑移量增大，上升段的斜率也变大。

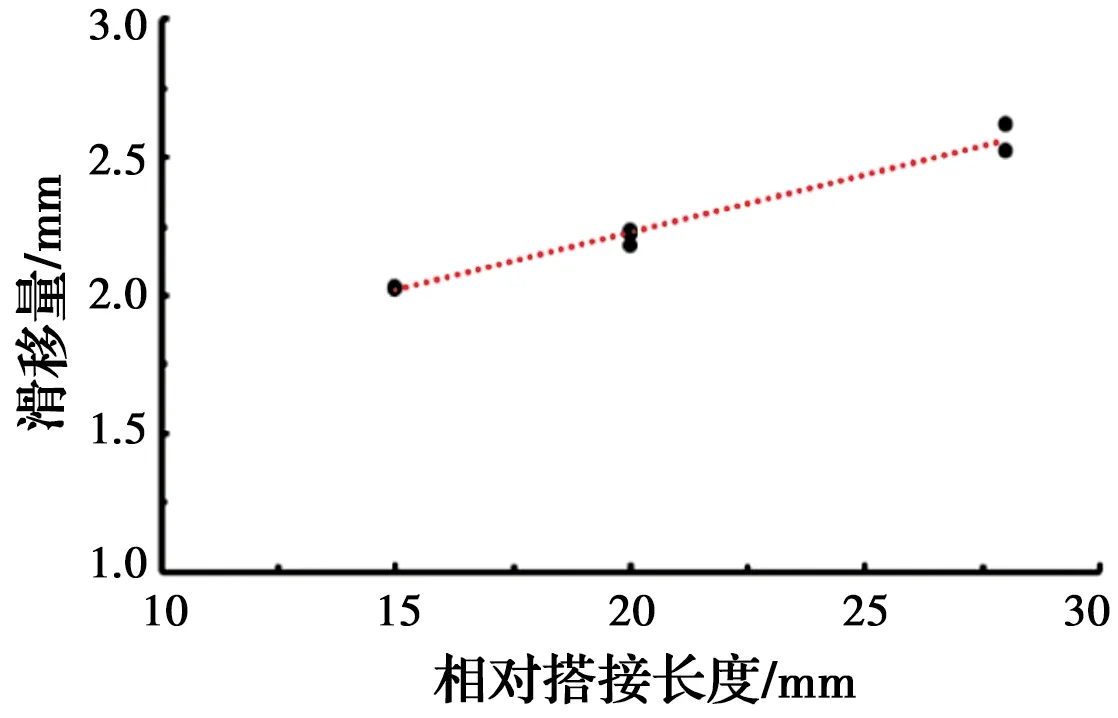
图10 相对搭接长度(la)与滑移量(sa)关系曲线图Fig.10 Curve of relative lap length (la) and slip (sa)

不同钢绞线直径试件相对搭接长度(la)与极限粘结应力(τa)的关系曲线如图11所示。从图中可以看出，搭接长度与搭接时的极限粘结应力呈负相关；搭接长度越长，搭接时极限粘结应力越低，该现象主要是由于在拉拔过程中沿搭接长度方向的粘结应力分布不均匀，随着搭接长度的减小，高应力区的相对长度增加，应力较为丰满，故其极限粘结应力越高，且搭接长度越小，其平均粘结应力越接近真实粘结强度。

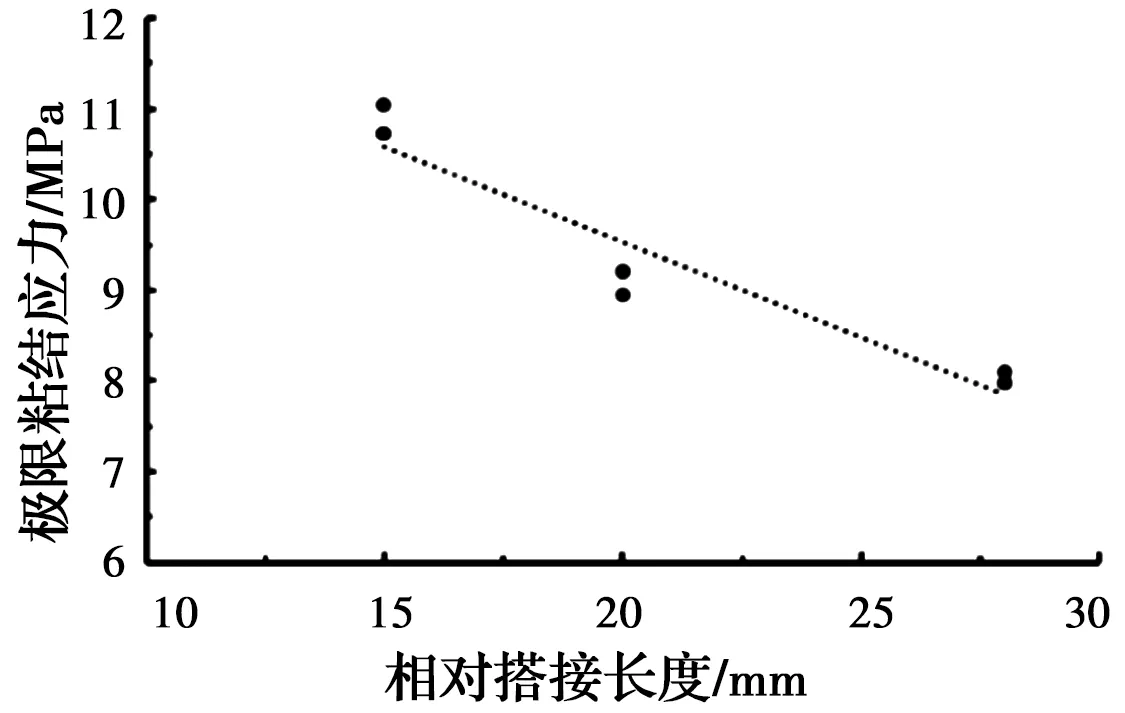
图11 相对搭接长度(la)与极限粘结应力(τa)关系曲线图Fig.11 Curve of relative lap length (la) and ultimate bond stress (τa)

3.3 钢绞线直径影响分析

横向钢绞线间距和搭接长度相同时，钢绞线直径不同的搭接试件的荷载-滑移曲线如图12所示。从图中可以看出，随着钢绞线直径的增加，相同荷载下所对应的滑移量减小。且钢绞线直径越大，试件极限拉拔力越大。达到峰值荷载时，滑移量越小，荷载滑移曲线上升段的斜率越大，“搭接刚度”越大。

图12 钢绞线直径不同试件的荷载-滑移曲线Fig.12 Load-slip curve of steel strand specimens with different diameter

图13为峰值荷载作用下，滑移量(sa)和极限粘结应力(τa)与钢绞线网直径(d)的关系曲线图。从图中可以看出，钢绞线直径与滑移量和极限粘结应力均呈负相关。随着钢绞线直径的增大，达到峰值荷载时的滑移量越小。钢绞线直径越大，搭接时极限粘结应力越低，该现象主要是由于泊松效应，钢绞线在受拉过程中，钢绞线沿径向产生收缩变形降低了两者的粘结性能，并随着钢绞线直径增加，泊松效应越明显，钢绞线产生的径向变形越大，从而导致钢绞线与ECC的粘结强度降低。

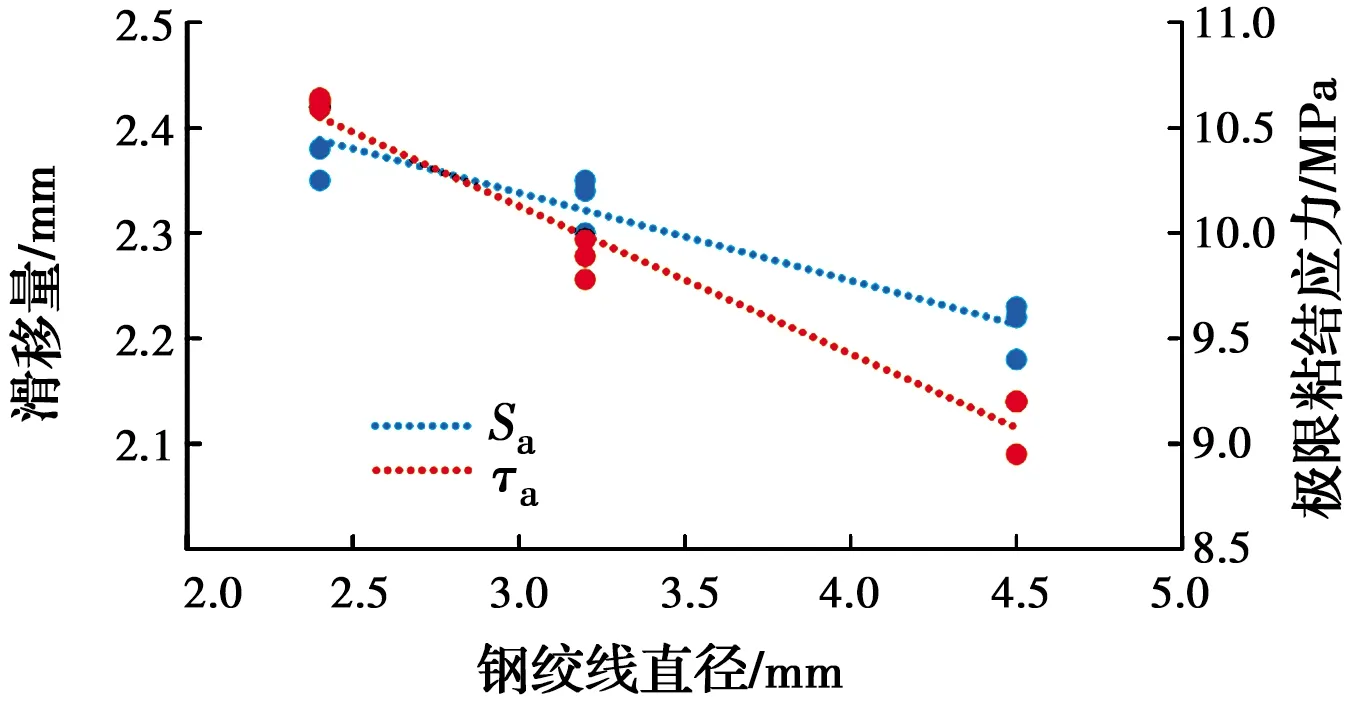
图13 峰值荷载下滑移量(sa)和极限粘结应力(τa)与钢绞线网直径(d)的关系曲线图Fig.13 Curve of the relationship between the peak load slip (sa) and the ultimate bond stress (τa) and the diameter of the stranded wire mesh (d)

4 临界搭接长度的确定

由搭接试验结果可以看出，当4.5 mm钢绞线在搭接长度为28d时，一个试件为钢绞线拉断破坏，两个试件为钢绞线滑移破坏；而搭接长度为32d的试件钢绞线全部被拉断。由此，可以将28d作为4.5 mm钢绞线的临界搭接长度。同理，3.2、2.4 mm钢绞线的临界搭接长度均为25d。

在临界锚固长度计算公式的基础上，引入修正系数β，得到临界搭接长度的计算公式

(5)

式中：la为临界搭接长度；d为钢绞线直径；fy为钢绞线极限抗拉强度；ft为ECC极限抗拉强度。

将上述结果及相关材性数据代入式(5)，进行数据拟合，结果如图14所示。基于试验结果，确定修正系数β=1.17，近似取为1.2。

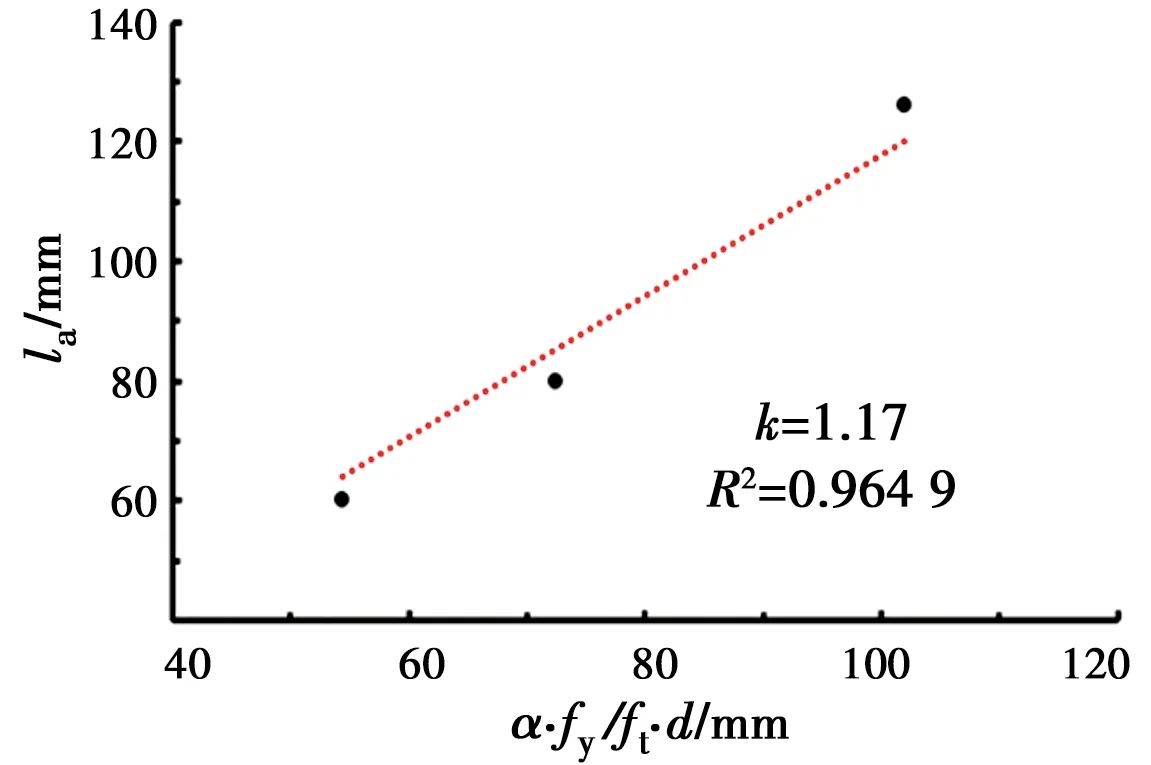
图14 修正系数拟合Fig.14 Modified coefficient fitting

5 结论

通过对4组39个高强不锈钢绞线网/ECC试件进行拉拔试验，分析了横向钢绞线间距、钢绞线直径及搭接长度对其搭接性能的影响规律，得出以下主要结论：

1)对于搭接试件，横向钢绞线的设置可以约束纵向钢绞线的滑移；在一定范围内，横向钢绞线间距越小，达到峰值荷载时滑移量越小，但不会改变搭接破坏时的脆性特征。

2)钢绞线网/ECC搭接时的极限粘结应力与钢绞线直径和搭接长度均成负相关。钢绞线直径越大及搭接长度越长，搭接时的极限粘结应力越小。

3)基于试验结果，确定了钢绞线网与ECC的临界搭接长度；并在钢绞线网/ECC临界锚固长度计算公式的基础上，提出了引入修正系数β的搭接长度计算公式。