改进双向LSTM的地震震相拾取算法

韩振华，郭浩雨，李 宇，张 玲，冯秀芳

(太原理工大学 信息化管理与建设中心，太原 030024)

震相到时拾取是地震学研究的重要课题之一。随着数字地震台网的大量建设，海量测震数据的产生，自动化快速精确识别震相对于地震学的研究有着重要的意义[1]。传统的自动拾取算法如STA/LTA(长短时窗比)[2]利用短时窗平均值与长时窗平均值比值的变化来反映能量的变化情况，存在依赖阈值选取的问题；模板匹配算法[3]是根据波形相似性进行判断，存在依赖模板、泛化性不好等问题。随着深度学习的快速发展，卷积神经网络以及循环神经网络在震相拾取方面也得到了应用：PEROL et al[4]应用8层的卷积神经网络对美国70万条连续地震波形数据进行了识别与定位，取得了较好的结果；赵明等[5]利用卷积神经网络对地震事件-噪声问题进行分类，该方法可识别大量人工标记遗漏的微震事件；蔡振宇等[6]提出基于小波时频谱的卷积神经网络模型对P波到时进行拾取，输入地震波形数据后可直接输出P波到时，具有运算速度快的特点；于子叶等[7]提出一种基于Inception网络结构的震相拾取算法，该方法通过神经网络的自适应提取波形特征对P波和S波到时进行拾取，使噪声数据有良好的稳定性；ZACHARY et al[8]提出一种基于门控循环神经网络的震相连接模型，该方法可将P波和S波在起始时间至12 s内发生的地震事件相关联；CHIN et al[9]提出了一种基于循环神经网络的实地震波检测算法，该算法可识别出实时发生的地震事件，同时可拾取P波和S波的到时。

RNN(循环神经网络)适合处理时间序列数据，被广泛应用于信号处理。鉴于波形数据实际上是一个在时域维度且具有前后相关性的连续变化过程的数据，并且循环神经网络在处理时序数据上具有优越性，因此将双向LSTM模型作为本文震相拾取的基本方法。双向LSTM模型可克服传统RNN模型梯度消失的问题[10]，同时可以将波形数据过去与未来的特征进行整合，从而辅助决策震相到时的预测问题。

本文通过对原始地震数据提取波形特征并预测P波到时，提出一种基于改进的双向LSTM模型的震相拾取算法。通过双向LSTM模型对波形数据进行自适应特征提取，同时采用Spatial-Dropout机制在随机区域对网络进行稀疏性约束以解决过拟合问题，最后通过引入Time-Distributed机制以充分利用波形数据前后时间步的特征信息并输出P波预测到时。

1 方法原理

1.1 数据预处理

本文采用地震台网人工标注震相到时的波形数据5 404条。从中随机挑选4 324条作为训练集，用于优化模型参数；685条作为验证集，用于判断训练停止时刻；395条作为测试集，用于验证模型的泛化能力。

数据预处理对于神经网络的训练有着重要的意义，预处理过程会直接影响模型收敛效果。本文的原始数据为时间窗口长度30 s的连续波形片段，数据的采样频率为100 Hz，因此数据格式为3 000×3的二维矩阵。由于波形数据中存在低频的长期背景扰动以及高频的噪声，这两者会导致模型在训练过程中接受过多的无用信号，从而降低拟合效果，因此首先对原始数据进行带通滤波。其次，地震数据中任意时间步的振幅差距过大，为了降低数据的方差，使损失函数的收敛过程更加平缓，需要对波形数据的每一道分量进行归一化操作：

(1)

式中：Ai为每一道分量中第i个采样点的振幅。

为避免原始数据较少而产生过拟合问题，在清洗后的波形数据中分别加入振幅最大值5%和10%的高斯噪声形成加噪数据来扩增训练数据量，最终形成16 212个地震事件数据集。图1表示对原始波形数据进行加噪处理，这里绘制出随机选取的两个地震数据分别加入5%，10%高斯噪声的对比图。

此外，本文提取出原始波形数据中P波到时，并将其前后0.3 s作为允许误差内的P波时间窗标签，其余时间步均标记为噪声。这样可将较长的时间序列数据预测某一时刻的回归问题转化为事件-噪声的二分类问题，从而提高模型的准确率。图2表示随机选取一个数据的标签处理前后对比，图2(a)为原始数据，红色线为P波到时；图2(b)为处理后的P波到时标签，可以看出处理后的P波到时信息与背景噪声对比明显，利于模型进行特征学习。

图1 数据加噪前后对比Fig.1 Comparison of data before and after adding noise

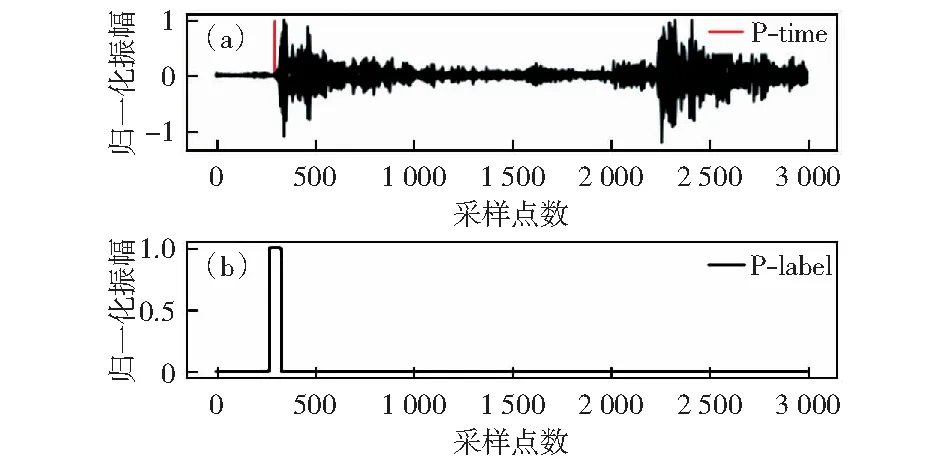
图2 数据标签处理前后对比Fig.2 Comparison of data before and after label processing

1.2 模型

1.2.1LSTM模型

长短期记忆(long-short term memory，LSTM)模型[11]是一种优化改进后的循环神经网络模型，可有效解决传统循环神经网络在训练过程中由长期依赖导致的梯度消失等问题[12]。LSTM由若干个记忆单元构成，其中每个记忆单元由细胞状态、遗忘门、输入门和更新门4部分组成。通过这些门的结构可让信息选择性的通过，用以去除或者增加信息到下一个细胞状态。图3表示LSTM单个记忆单元结构。

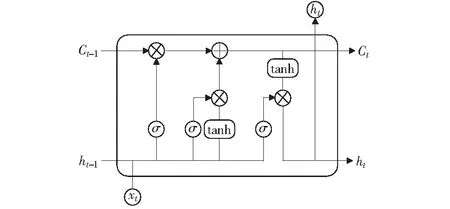
图3 LSTM单个记忆单元结构Fig.3 Single memory cell structure of LSTM

1) 细胞状态(Ci)，存储当前时间步的特征信息，在所有链式记忆单元中传递。

2) 遗忘门，用于控制遗忘上一层细胞状态的内容，根据上一时间步的输出hi-1和当前时间步的输入xi，通过sigmoid函数将其映射为[0,1]之间的向量fi，表示上一层细胞状态信息的保留程度，0代表全部遗忘，1代表全部保留。其公式为：

fi=σ(Wf[hi-1,xi]+bf) .

(2)

式中：W和b分别是LSTM模型的权值和偏置，均为模型的训练参数；σ是激活函数sigmoid.

3) 输入门，通过处理当前时间步的输入确定需要更新的信息并更新细胞状态。首先，利用sigmoid函数生成更新程度it；其次，利用tanh函数生成含有待更新信息的候选向量Ct；最后用遗忘门的输出ft与上一时间步的细胞状态Ct-1相乘，丢弃需遗忘的信息；再将it与候选向量Ct相乘，得到更新后的信息，二者相加得到本时间步的细胞状态。其公式为：

it=σ(Wi[ht-1,xt]+bi) .

(3)

Ct=tanh(Wc[ht-1,xt]+bc) .

(4)

Ct=ft⊗Ct-1+it⊗Ct.

(5)

其中，⊗为逐点乘积。

4) 输出门，基于细胞状态保存的信息选择性的输出细胞状态Ct的内容。通过sigmoid函数输出信息被过滤的程度Ot，再利用tanh函数将当前细胞状态中的信息映射在[-1,1]之间，二者相乘后即得到当前时间步的输出h.其公式为：

Ot=σ(Wo[ht-1,xt]+bo) .

(6)

ht=Ot⊗tanh(Ct) .

(7)

1.2.2改进的双向LSTM模型

尽管LSTM模型可解决传统RNN长期依赖的问题，但是没有利用未来的信息[13]。为同时考虑数据的过去以及未来信息，本文采用双向长短期记忆(Bi-Directional LSTM，Bi-LSTM)模型，其网络结构如图4所示。该模型的工作原理是通过前向LSTM层与反向LSTM层叠加，将原始序列数据输入前向LSTM层并把数据的反向副本输入给反向LSTM层，由此得到相反的两个序列隐藏层状态ht和h＇t，再将其连接得到预测输出yt.

在数据有限的情况下，训练参数过于庞大的神经网络会产生过拟合，即模型在训练数据上完美契合，但泛化能力较差[14]。针对双向LSTM模型对波形数据进行预测存在过拟合的问题，引入Spatial-Dropout机制，在模型的随机区域进行稀疏性约束。Spatial-Dropout机制是2015年由TOMPSON et al[14]提出的一种Dropout方法，普通的Dropout会随机地将部分元素置零，而Spatial-Dropout会随机地将部分区域置零，对于地震波形这种时序数据来说，将一段信号随机置为0可以减少过拟合的风险。其具体原理是以[0,1]之间的概率(一般为0.5)对部分区域的神经元进行随机失活处理，失活后的神经元会在该次迭代中无法更新权重和偏置，由此使得模型无法通过记忆固有信息特征来完成震相到时的拾取，从而将模型变得稀疏化，解决了模型的过拟合问题。其公式为：

r(l)=Bernoulli(p) .

(8)

(9)

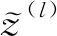
如图4所示，为了对地震波形在时域上实现“多对多”的到时预测，通过Time-Distributed机制对每个时间步应用全连接层，通过设置sigmoid为激活函数即可从时域维度进行事件-噪音的二分类，从而输出P波到时。

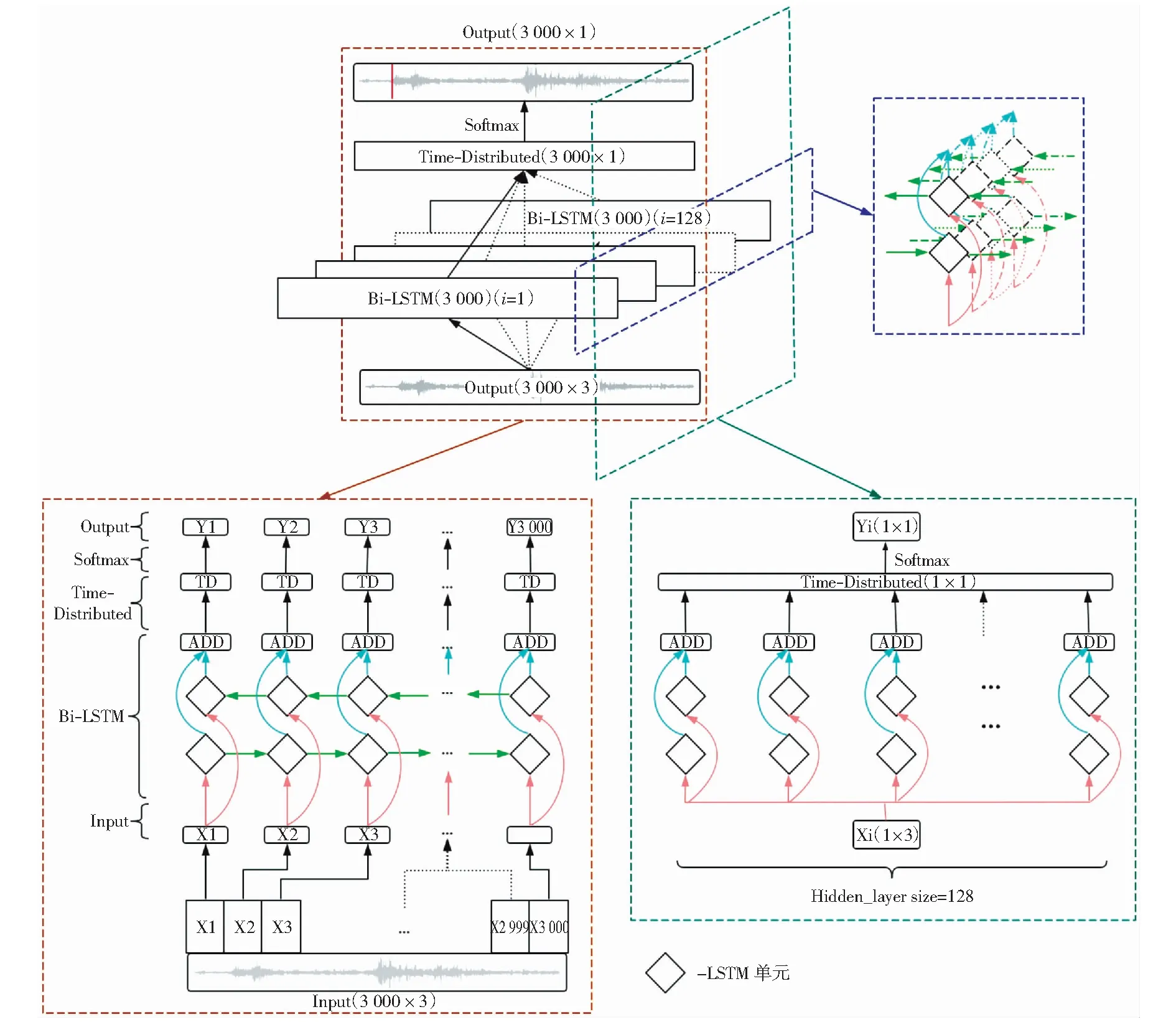
图4 基于Bi-LSTM的P波拾取网络结构图Fig.4 Network Structure of P wave picking based on Bi-LSTM

基于双向LSTM的P波拾取算法流程如图5所示。整个流程由2部分组成：第一部分为数据预处理部分，对数据进行滤波、加噪与归一化；第二部分为深度神经网络部分(见图4)，由4层构成，分别是Input层、Bi-LSTM层、Time-Distribution层和输出层。数据经由预处理部分处理完毕后，由输入层输入预处理好的3 000×3的地震信号三分量数据(波形时长为30 s，采样率为100 Hz)；Bi-LSTM层由双向LSTM单元组成，实现地震信号进行时域分析。如图4所示，Bi-LSTM层中，内部有2个LSTM，分别是Forward层和Backward层，表示前向和后向，在Forward层从1时刻到t时刻正向计算一遍，在Backward层从末尾开始逆向计算一遍，得到并保存每个时刻正向与逆向隐含层的输出。最后在每个时刻结合Forward层和Backward层的相应时刻输出的结果进行拼接得到最终的输出。每个LSTM单元的隐藏节点个数为128，输出128维的特征向量。为了避免过拟合，利用Spatial-Dropout机制对模型进行稀疏化约束，对双向LSTM输出的特征使用ADD方式结合，输出3 000×128的特征向量；Time-Distributed层对每个时间步的128维特征进行全连接分类；每个时间步的输出结果进行Softmax运算后，由输出层输出3 000×1的One-Hot标签，实现P波的位置的输出。

图5 基于改进双向LSTM的P波拾取算法流程Fig.5 P wave picking algorithm flow based on improved Bi-LSTM

1.3 训练过程

在模型训练方面，本文使用均方根梯度下降算法(root mean square prop，RMSprop)作为优化器，初始学习率为0.001并设置为学习率衰减，使用交叉熵损失函数(cross entropy error function)来对模型进行参数寻优。此外，通过将训练数据划分为训练集和验证集，训练集用于计算梯度以及更新参数，用验证集来判断训练停止时刻，即在近5次迭代训练时若出现验证集误差升高则停止训练，同时返回模型参数。

2 实验结果与分析

2.1 评价指标

为了更好地对模型进行评估，本文使用精准率P和召回率R作为模型评价指标。具体公式如下：

(10)

(11)

式中：TP为真正例，即模型识别的事件是真实的地震事件，相反FP则为假正例；TN为真反例，即模型识别的噪声是真实的噪声，相反FN则为假反例。精确率反映模型的误检率，精确率越高说明误检率越低；召回率反映模型的漏检率，召回率越高说明漏检率越低。

2.2 结果对比

经过35个epoch的训练，本模型最终在训练集上精确率达到87%，召回率达到82%；在测试集上精确率达到90%，召回率达到92%，其训练过程的精确率与召回率如图6所示。为从不同角度验证本文算法在震相到时预测问题上的适用性和优越性，在测试集上与CAI et al[15]和ZACHARY et al[8]中的算法展开综合对比，其对比结果如表1所示。

由表1可知，本模型在测试集上的精确率比LSTM高6%，比GRU高5%；在召回率上比LSTM高38%，比GRU高39%.表明本模型在不同的评估标准上均取得了更优的结果。

此外，为了便于评价模型的泛化能力,将在测试集上预测的P波到时误差分布做成直方图，如图7所示。图7显示395个测试集中的波形数据通过双向LSTM模型计算得到的P波拾取结果与人工拾取到时之间的误差分布，其中303条预测结果误差小于0.1 s，占比76.7%；375条预测结果误差小于0.2 s，占比94.2%；393条预测结果误差小于0.5 s，占比99.5%；2条预测结果误差大于1.0 s，占比0.5%.对其中到时拾取误差小于0.1 s和大于1.0 s的数据分别绘制出波形图进行分析，结果如图8所示。其中红色线为人工拾取的P波到时，蓝色线为模型拾取的P波到时。

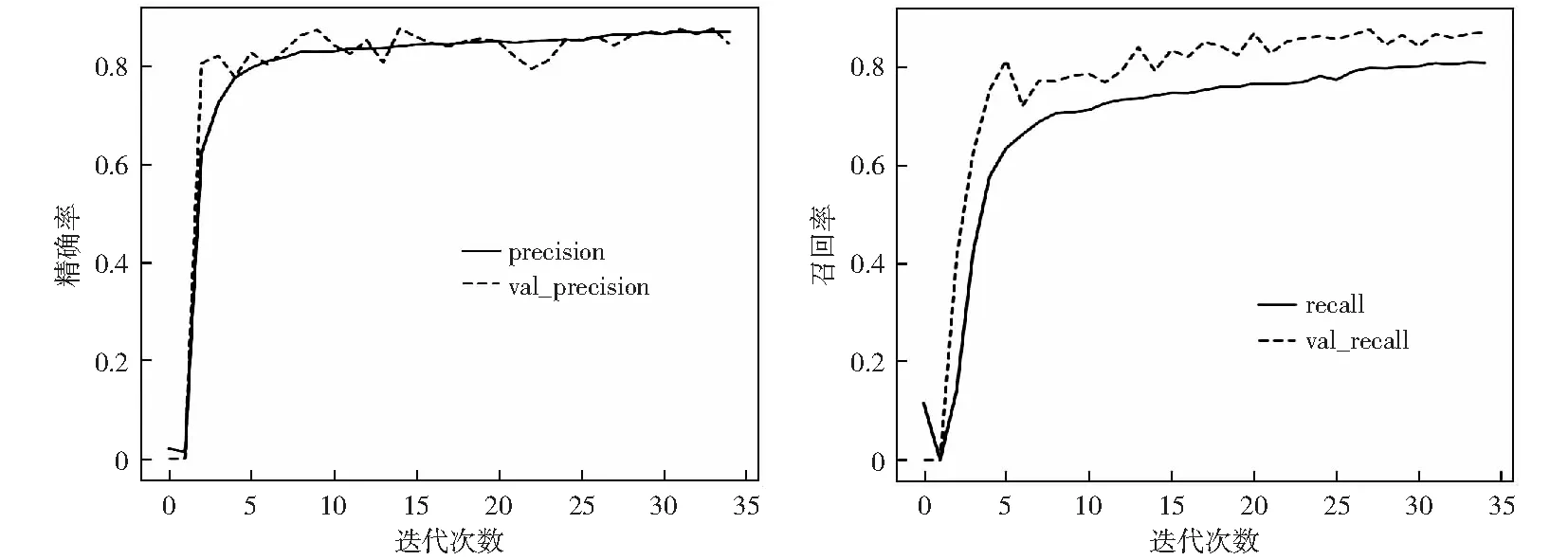
图6 训练过程的精确率和召回率Fig.6 Precision and recall rate of the training process

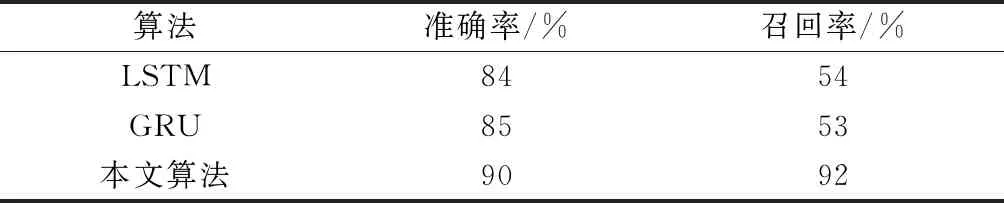
表1 不同算法在测试集上的比较结果Table 1 Comparison results of different algorithms on the test

由图8分析可知，图8(a)中模型拾取的P波到时比人工拾取滞后了0.02 s，由于人工拾取到时的标注精度是0.1 s，故认定该拾取结果准确；图8(b)中模型拾取的P波到时比人工拾取提前了1.47 s，在人工拾取到时的标注精度之外，认定该拾取结果误差较大。其中，图8(a)的数据噪声信号较少，即信噪比较高；而图8(b)的数据参杂过多的噪声干扰，即信噪比较低。因此分析认为本模型对信噪比较低的数据的拾取有一定的偏差，即在噪声干扰过强的情况下可能会影响模型的拾取效果。

图7 模型拾取到时与人工拾取到时的误差分布Fig.7 Error distribution between model picking and manual picking

图8 模型对高信噪比和低信噪比数据的到时拾取对比Fig.8 Comparison of the model's time picking of high SNR and low SNR data

为了验证数据加噪对模型泛化能力的提升，本文做了噪声训练对比如图9所示。从图9中可以分析得出，用未加噪数据训练的模型对加噪数据的P波拾取效果较差，而用加噪数据训练后的模型对加噪数据的P波拾取效果更为准确。分析认为P波信号振幅较小，在噪声干扰下容易被过多地覆盖，因此在测试中未能有效识别其完整的波形特征，导致拾取效果不佳，而通过用加噪数据进行训练可提高模型对P波周围噪声干扰的忍耐度，提高了模型的泛化能力。

3 结束语

本文提出一种基于改进双向LSTM的震相到时检测算法，首先对原始波形数据进行预处理，其次通过双向LSTM模型对地震信号数据进行前向和反向的特征信息提取。利用Spatial-Dropout机制解决模型的过拟合问题，最后结合Time-Distributed机制实现P波到时预测。实验结果表明，本文方法比LSTM、GRU等传统RNN方法在震相到时预测问题上更具优越性。同时，与CNN等方法不同的是，本文算法从时间维度将过去和未来的波形特征进行整合并且将振幅变化和时间的相关性联系起来，因此大大减少了震相到时预测问题的误差。此外，本文利用不同比例的加噪数据进行训练测试，验证了模型的泛化能力。最后，改进的双向LSTM作为深度学习的方法之一，与STA/LTA、模板匹配等传统波形检测方法进行对比，本文模型不需要人工设定阈值，且对低信噪比数据有较高的准确率和召回率，其灵活性和普适性更强。

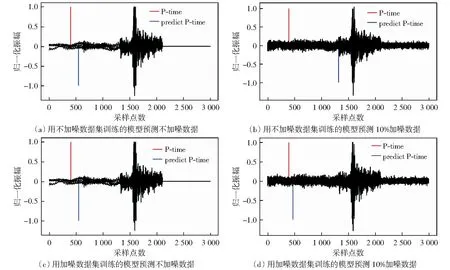
图9 噪声训练对比Fig.9 Comparison of noise training