空间相机匀速扫描干扰补偿控制方法

张艾，林喆，李婧，李寅龙

北京空间机电研究所，北京 100094

作为全球发展最为迅猛的高科技技术之一，地球卫星对地遥感技术是利用卫星上搭载的可见光、红外和微波等传感器，收集地球表面和近地空间的电磁辐射数据，探测和识别地球资源和环境信息的空间技术[1-4]。空间相机对于卫星来说，如同人的眼睛，是实现卫星对地观测的重要手段[5]。

为增大覆盖范围，星载相机可以采用相机整体沿垂直卫星飞行方向转动扫描成像的方案，根据这种扫描型相机的工作原理，相机主体扫描运动的控制精度是限制相机的成像质量提高的重要因素，要想得到较高的成像质量，必须实现对扫描运动的精确控制。永磁同步电机(permanent magnet synchronous motor，PMSM)因其具有惯性低、转换效率高、调速性能出色的特点，作为驱动部件被广泛应用于空间扫描成像系统。

实际永磁同步电机伺服系统是一个非线性、强耦合的系统，在永磁同步电机的运行过程中，存在周期性干扰与非周期性干扰。周期性干扰一般由负载转矩和永磁同步电机自身的通量谐波、齿槽转矩、定子电流测量误差、死区时间等因素引起[6-8]。周期性干扰对系统的稳态性能影响更加明显，会导致控制系统出现稳态波动，从而限制了PMSM在空间相机高精度扫描成像系统的应用。因此，抗干扰控制研究是目前空间相机扫描成像系统研究的重点之一。目前对于永磁同步电机稳态波动的抑制主要靠使用更为先进有效的控制算法来实现。这些方法主要分为两大类：状态观测器抗扰控制方法和基于内模原理的抗扰控制方法。

状态观测器的抗扰控制一般在系统中引入非线性干扰观测器作为实时补偿器，以抵抗扰动并减少不确定性。文献[9]将Backstepping算法和前馈控制，等价输入干扰(equivalent input disturbance，EID)估计相结合，设计了PMSM鲁棒抗扰控制策略，有效提升了系统的动态跟踪性能和抗干扰特性；文献[10]提出了一种基于有限时间扰动观测器的PMSM自适应非奇异终端滑模控制器，具有较好的跟随效果并减小了超调量；文献[11]利用状态变量构造干扰观测器，得到基于线性矩阵不等式的干扰观测器存在条件和设计方法。文献[12]采用双曲正切函数替代传统的开关函数，设计了改进型滑模观测器，能有效地抑制传统型滑模观测器中的抖振过大问题。基于状态观测器的抗扰控制方法可有效降低扰动对系统稳态性能的影响，但其设计较为复杂，会在一定程度上降低控制软件的可靠性，对于长期工作在电磁辐射较强的近地空间环境中的空间相机扫描系统并不适用。

基于内模原理的抗扰控制一般通过在速度环控制器中嵌入周期性干扰的内模的方法抑制扰动。文献[13]提出了一种在速度环PI控制器中嵌入内模环节的方法来抑制PMSM的稳态速度波动；文献[14]通过模型预测控制方法抑制扰动力矩；文献[15]提出了一种基于内模原理的变增益鲁棒二自由度速度调节器；基于内模原理的抗扰控制器设计思路清晰、步骤简单，但计算量较大，占用较多的星上计算资源。

本文结合敏感器测量输出和系统模型估计干扰量，在此基础上采用一个对输出产生相反影响的超前输入补偿量来快速抑制扰动影响。较好的解决了空间相机扫描控制系统中的正弦扰动问题，可有效改善速度稳态波动，满足成像需求。

1 PMSM建模

对于空间相机扫描控制系统执行机构和测量敏感器的选取，必须考虑其是否适应在空间环境长期工作。由于角度传感器的制造精度较速度传感器高，所以高精度的控制中普遍采用角度信号作为控制的反馈手段。针对空间相机扫描控制系统对传感器的要求,在综合考虑传感器的精度、体积、质量，并重点考虑对发射环境和长期空间工作环境的适应性，选用绝对式光电编码器作为角度反馈元件。为了尽可能减小转矩波动，选取三相无齿槽永磁同步电机作为执行机构。

将三相永磁同步力矩电机进行Clarke和Park变换[16-17]，dq轴系下的电机模型为：

(1)

式中：Ld，Lq分别为直轴(d轴)、交轴(q轴)线圈电感，为常数；ud，uq分别为d轴、q轴等效输入电压；id，iq分别为等效电流；Te为电机输出转矩；R为定子电阻；p为电机极对数；ωr为转子机械角速度；λ为由转子永磁体产生的定子绕组的磁链。

在转矩方程Te=1.5p[λiq+(Ld-Lq)idiq]中，第一项为交轴电流与转子励磁磁链的乘积，代表电磁转矩，第二项为磁阻转矩，对于面装式转子的三相永磁同步力矩电机，Ld=Lq=L，Te的表达式简化为：

Te=1.5pλiq

(2)

由式(2)可知，电机输出转矩与id无关，因此可采用id=0控制，令id=0，iq可控。对面装式永磁同步电机而言，id=0控制即为力矩电流比最大控制。

2 控制系统设计

要实现高精度的速度与角度控制，目前主要采用角度反馈与速度反馈，电流反馈相结合的方法。电流环的主要作用是改造内环控制对象的传递函数，提高系统的快速性并及时抑制电流环内部的干扰。速度环的作用是增强系统抗负载扰动的能力，抑制速度波动。位置环的作用是保证系统静态精度和动态跟踪的性能，直接关系到直流伺服系统的稳定与高性能运行，而且它是反馈主通道[18]。一个高性能控制系统的设计，需要针对各个闭环的具体作用和要求，采取相应的控制方式[19]。

对于本文分析的系统，采用id=0控制时，PMSM模型可以简化为：

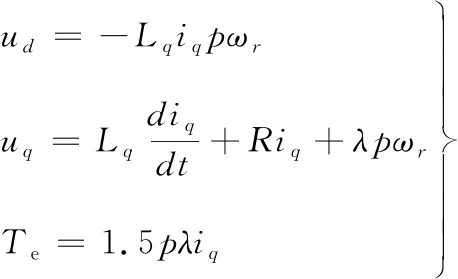
(3)

在工程实现中，考虑到电路的复杂程度，电路的可靠性，元器件的等级，空间环境适应性等问题，往往可以省略掉电流环，简化硬件电路。此时id=0控制变为ud=0控制。

图1 PMSM矢量控制系统结构Fig.1 The structure of PMSM vector control system

ud=0在特定条件下可以简化。当电机转速较低，电感较小时(即Ldωr<103(H·rad)时)，可近似认为Ldpωr≈0，式(1)可简化为：

(4)

式(4)可以等效为如图2所示的直流电机模型。

图2 等效直流电机模型Fig.2 The model of equivalent DC motor

式中：Kt为电流力矩系数，满足Kt=λp；Ks为反电动势系数，满足Ks=1.5λp；J为电机转动惯量。

当PMSM存在转矩扰动时，速度、位置双闭环控制的系统框图如图3所示。

图3 等效直流电机模型双闭环控制框图Fig.3 The frame of double-loop control for equivalent DC motor

为了实现转速无差，速度环按Ⅱ型系统设计，并选速度调节器为PI调节器。因为控制对象运动速度较低，且控制对象加工精度较高，相对稳定,因此位置控制环可以采用PID控制实现要求。

3 扰动力矩超前补偿

(1)求解干扰力矩Tf

为了求解干扰力矩的表达形式，首先考虑系统不存在干扰力矩的理想情况，在图3中，选择合适的位置环和速度环控制率G1和G2，当系统达到稳态后，稳态误差应为0。此时系统输出角度θ1(t)与位置指令θ*(t)相等，满足θ1(t)=θ*(t)。当电机存在干扰力矩Tf(t)时，系统有位置指令和干扰力矩Tf(t)两个输入，根据线性系统的叠加原理，两个输入对应的输出满足如下关系：

θ(t)=θ1(t)+θ2(t)

(5)

式中：θ1(t)为位置指令对应的输出；θ2(t)为Tf(t)对应的输出。当系统达到稳态后，有：

θ2(t)=θ(t)-θ1(t)=θ(t)-θ*(t)

(6)

将两个输入引起的输出进行分离，只考虑干扰力矩Tf(t)作用于系统的部分，图3的系统框图可简化为图4的形式。

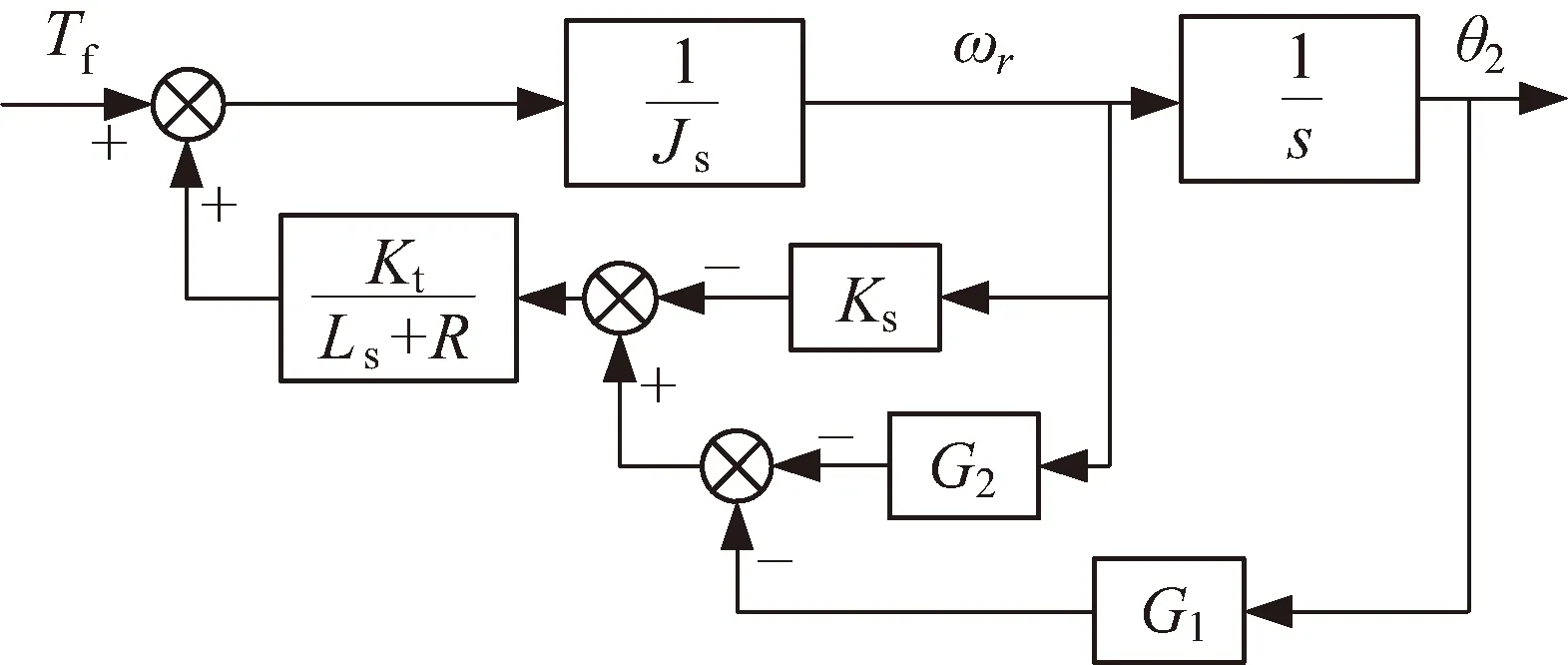
图4 干扰力矩作用下的系统框图Fig.4 The control frame of system under disturbance torque

可求得图4中传递函数的表达式为：

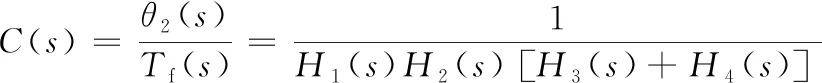
(7)

其中：

H4(s)=Kt(G1+sG2+sKs)。

画出C(s)的波特图，查找C(s)的波特图中对应角频率下的幅值增益和相角移动，则可根据实测的θ2(t)反推出Tf(t)。

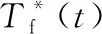
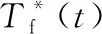
图5 等效直流电机模型速度环控制框图Fig.5 The frame of speed loop control for equivalent DC motor

图6 仅考虑完全补偿Tf情况下的系统框图Fig.6 The control frame when Tfcan be

(8)

4 系统仿真与试验结果

为了验证本文提出的超前补偿方法应用于实际扫描控制系统中的效果，采用一个空间相机扫描控制地面模拟平台对算法进行实验验证。该平台由空间相机扫描机构及模拟载荷、三相永磁同步电机、光电编码器与扫描控制电路构成，电机与机构负载参数如表1所示，按照设定的扫描规律，相机模拟机构先经过一个匀加速缓起过程加速到60°/s后固定，实现角度由-180°到+180°的单向连续匀速变化，对地及各定标位置成像。

表1 PMSM参数

由于在实际系统中，角度θ信号中存在大量噪声。来源主要是光电编码器测量误差与FPGA数据采集误差。FPGA数据采集误差一般为稀疏野值，可通过软件校验剔除；光电编码器测量误差一般为随机噪声，本文地面模拟平台选用的高精度绝对式光电编码器测角误差为亚角秒量级，该误差对位置环控制率影响很小，可以忽略不计；但对速度环控制率影响较大。这是因为系统中没有测速敏感器，速度反馈量ωr由角度θ差分而来，在较小的采样时间下差分过程会极大的放大测量噪声，造成反馈量ωr与实际速度误差过大，影响速度环控制精度。因此，需要在速度环反馈回路中添加一个低通滤波器，对反馈量ωr进行处理，使之更接近真实转速。

4.1 仿真分析

由于实际系统中大量采用数字控制器，故采用离散系统模型，采样周期和控制周期均为250μs，在Simulink中建立PMSM的等效直流电机控制模型。速度环控制器采用PI控制，位置环控制器采用PID控制。

定义输出角度与指令的差eθ为系统角度跟踪精度，表达式为：

eθ=θ(i)-θ*(i)

(9)

由于无法直接测量速度，用10 ms的转动角度误差Δθ10ms表征系统的速度跟踪精度。Δθ10ms表达式为：

(10)

θ2(t)≈[1.516cos(25.13t)-

1.012sin(25.13t)]×10-4

(11)

A1=1.094×10-3,φ1=-1.091 rad

(12)

反推出：

=0.146cos(25.13t)+0.0802sin(25.13t)

(13)

图7 从Tf(s)到θ2(s)的传递函数波特图Fig.7 Bode plots from Tf(s)toθ2(s)

A2=1.680,φ2=-0.010 89 rad

(14)

反推出：

=0.086 4cos(25.13t)+0.048 7sin(25.13t)

(15)

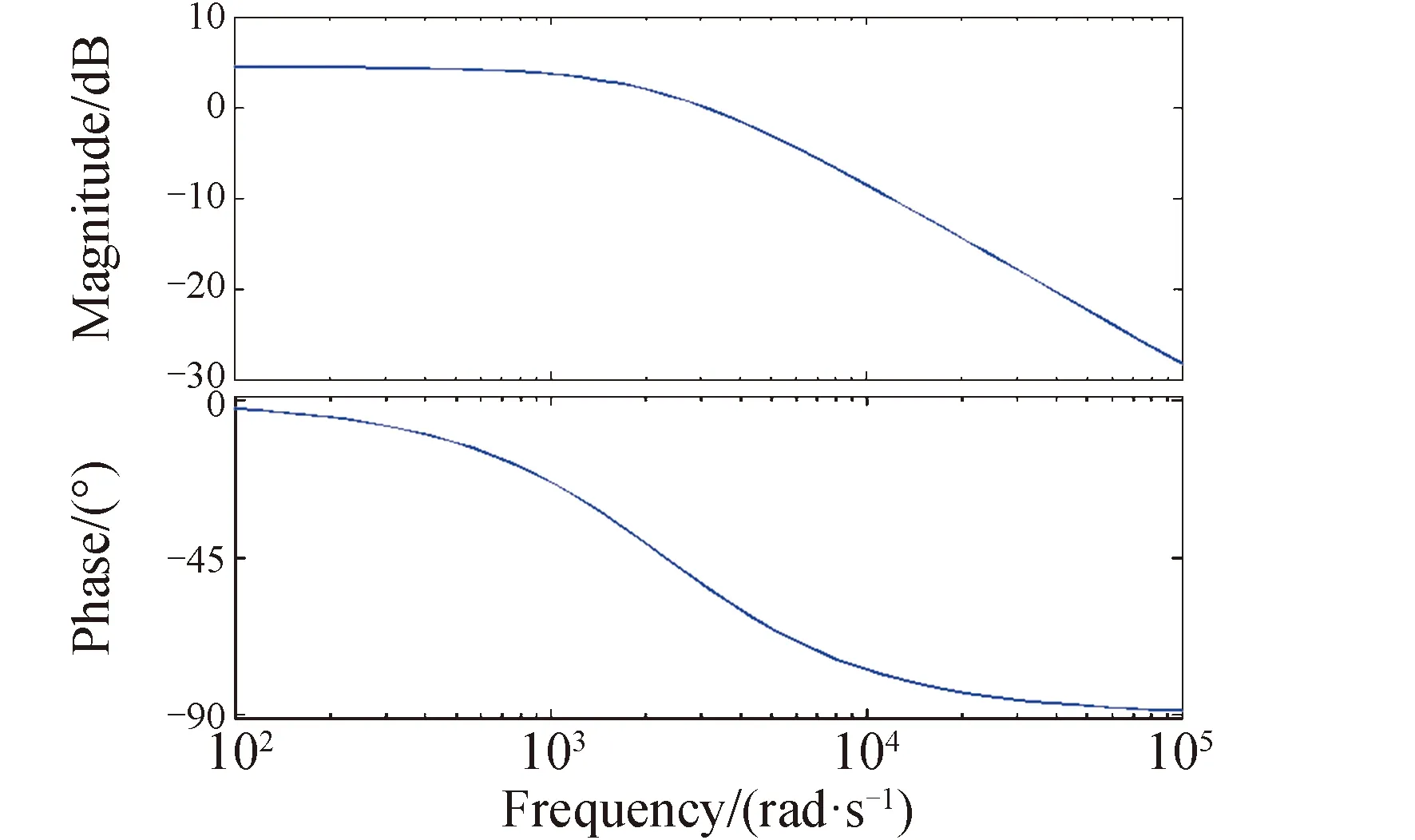
图8 从到Tf(s)的传递函数波特图Fig.8 Bode plots from to Tf(s)

图9 Simulink仿真补偿前后的角度跟踪精度Fig.9 The angle tracking accuracy before and after compensation for Simulink simulation

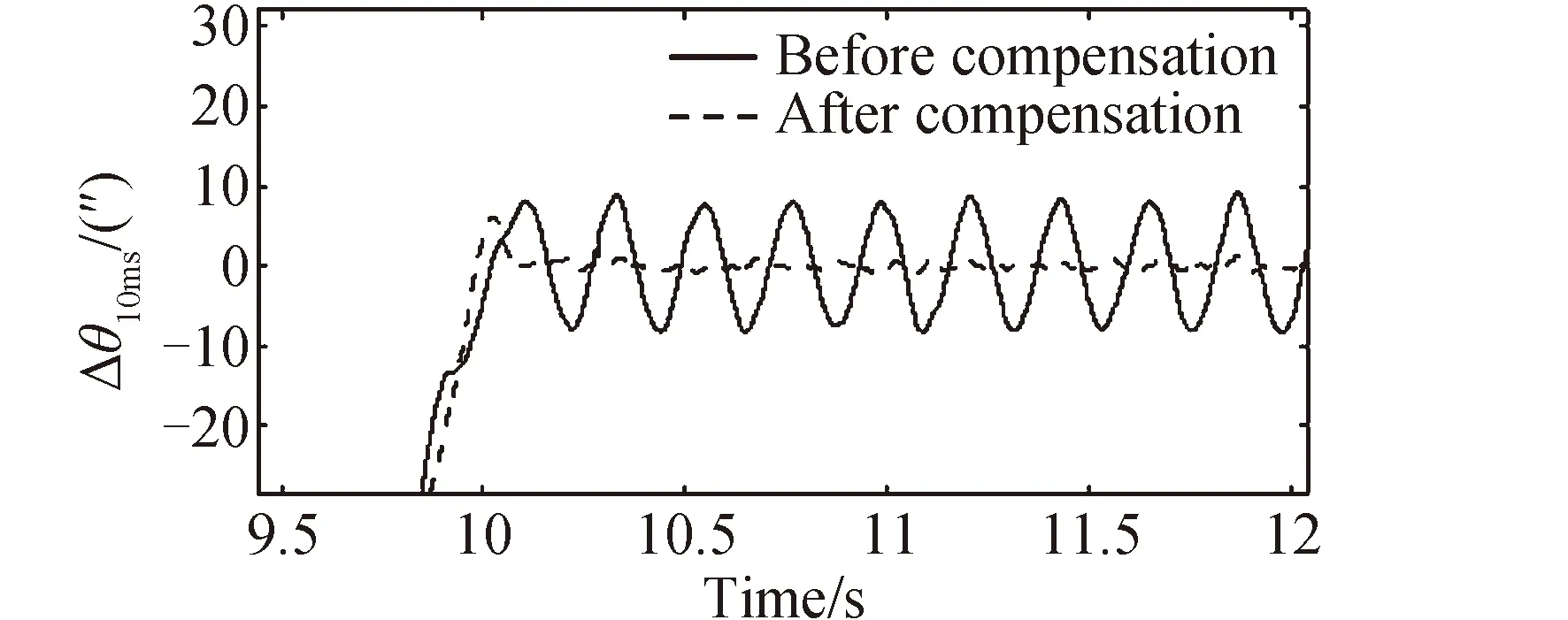
图10 Simulink仿真补偿前后的速度跟踪精度Fig.10 The velocity tracking accuracy before and after compensation for Simulink simulation

4.2 实验验证

将本文提出的控制方法应用于地面模拟平台中进行实验，使用LabView采集模拟负载转动角度数据，按照图3所示的等效直流电机双闭环控制模型进行控制，控制算法与4.1节Simulink仿真相同，算法通过CCS软件编写。

2.013sin(25.14t)]×10-4

(16)

利用本文所述方法，根据理想系统模型的传递函数C(s)和C1(s)可以推出:

=-0.103cos(25.14t)+0.199sin(25.14t)

(17)

=-0.062 6cos(25.14t)+0.117 8sin(25.14t)

(18)

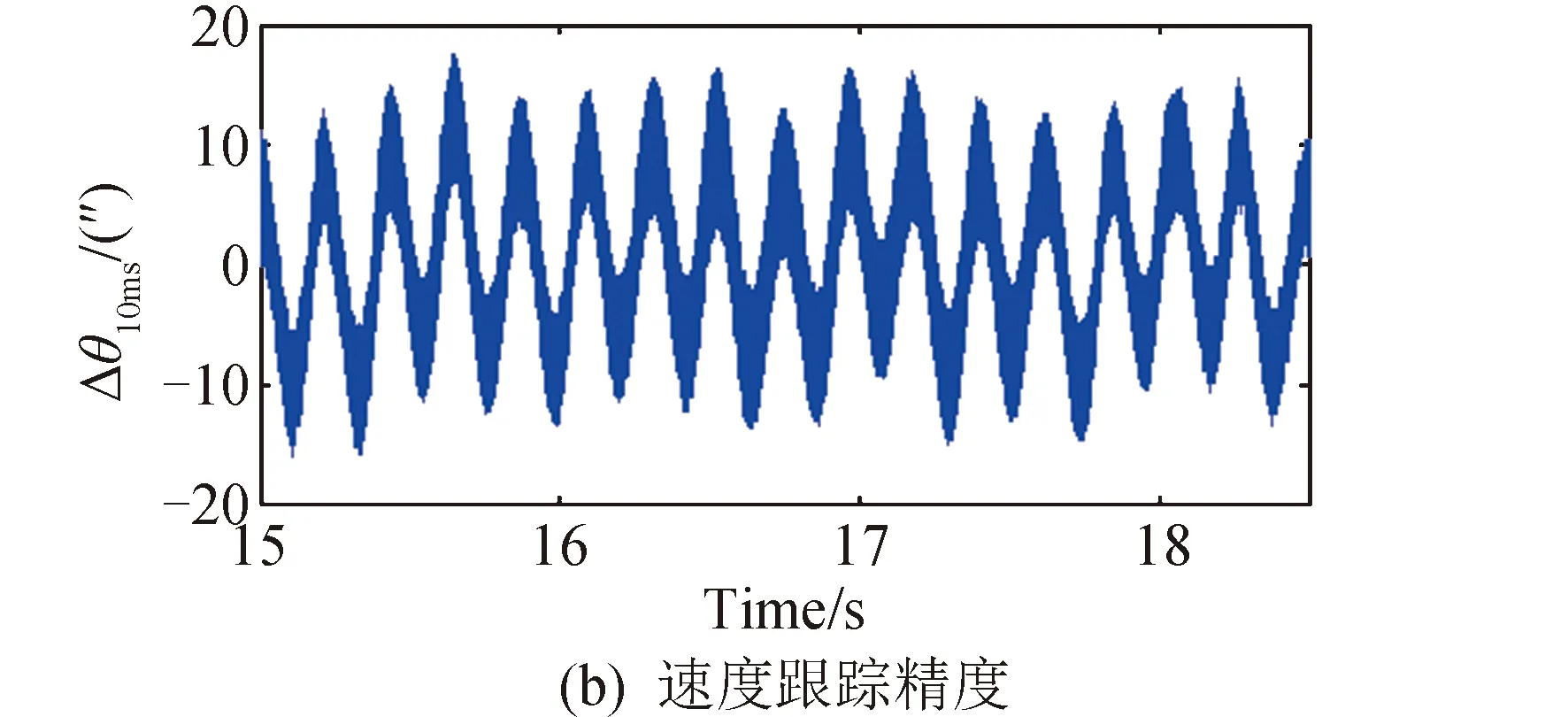
图11 实验平台补偿前跟踪精度Fig.11 The control accuracy before compensation for verification platform

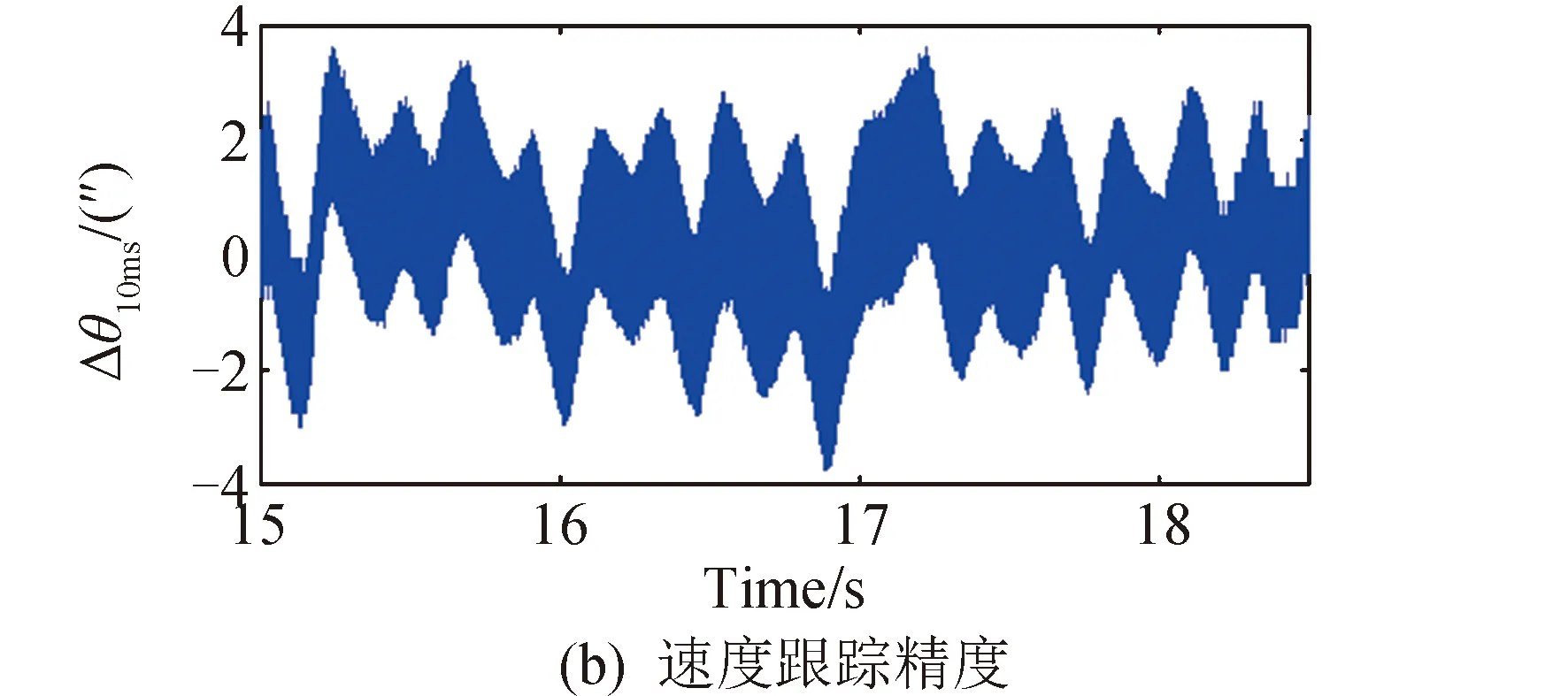
图12 试验平台补偿后跟踪精度Fig.12 The control accuracy after compensation for verification platform

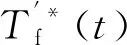
数学仿真和实验验证均说明了该方法对匀速扫描系统中存在的正弦干扰力矩有一定的补偿作用，可以降低速度波动，提高稳态速度控制精度。但由于实际系统中还存在非周期性的干扰，作用于电机上的干扰力矩并非十分理想的正弦形式，该超前补偿方法在实际系统中效果达不到Simulink仿真的水平。

5 结束语

本文考虑较大惯量空间相机成像扫描控制系统，针对永磁同步电机匀速转动存在的正弦干扰力矩，提出了一种扰动补偿方法。该方法应用线性系统叠加原理，在速度、位置双闭环的基础上，采用超前补偿控制策略来设计系统控制器，克服了传统方法系统复杂程度高和计算量大的缺点。仿真和实验结果表明，与补偿前相比，本文提出的方法大幅提高了系统角度和速度跟踪精度，对相机在空间环境中保持高精度、高可靠、长寿命工作具有重要意义。